ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 18 страница

(16.89)

где х_k- значение случайного процесса в момент времени t_k.

Равенство (16.89) означает, что значение случайного процесса в выбранный момент времени t_n зависит только от того, какое значе­ние случайный процесс принял в предыдущий момент времени t_n-1,

и не зависит от того, какие значения принимал случайный процесс в предыдущие моменты времени. Таким образом, вся информация о марковском процессе содержится в двумерной ПРВ. С учетом (16.89) и исходя из определения условной ПРВ для марковского процесса n-мерную ПРВ можно определить как

(16.90)

Если ПРВ зависит только от интервала времени между сосед­ними моментами t_k- t_k-1 то процесс Маркова является стационар­ным. При х₁= х₂=...= х_n= х дпя стационарного марковского процесса запишем

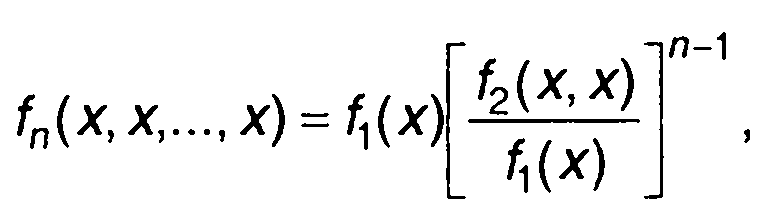(16.91)

что соответствует равенству в (16.68).

Запишем выражение для ПРВ марковского процесса при n = 3 в виде

(16.92)

Интегрируя по х₂ левую и правую части равенства, получаем

(16.93)

Учитывая определение условной ПРВ

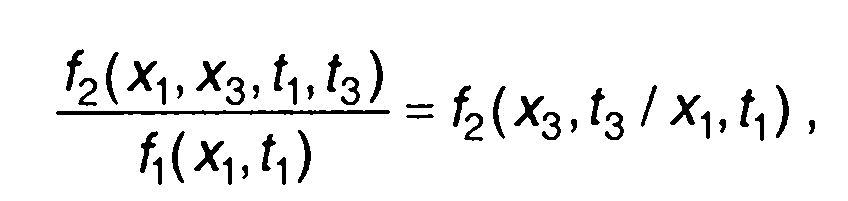(16.94)

выражение (16.93) запишем в виде

(16.95)

Уравнение (16.95) называется уравнением Смолуховского, или обобщенным уравнением Маркова. Для стационарного марковского процесса уравнение Смолуховского записывается в виде

7

(16.96)

Из уравнения Смолуховского может быть получено дифферен­циальное уравнение перехода непрерывного марковского процес­са. С учетом обозначений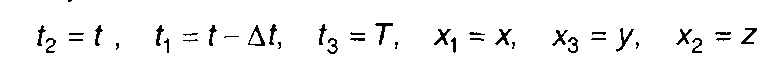

дифференциальное уравнение запишется в виде

(16.97)

где

(16.98)

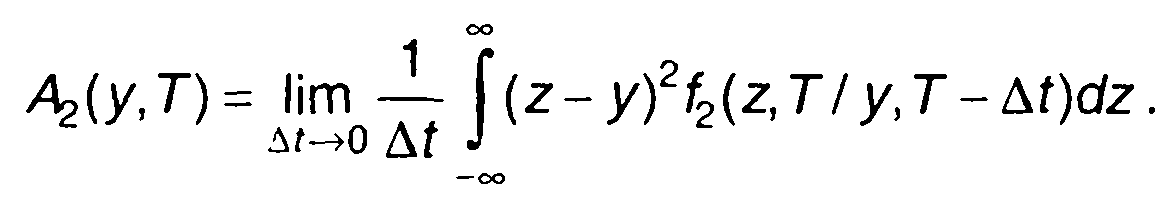(16.99)

Уравнение (16.97) называется первым уравнением Колмогорова. Плотность распределения вероятностей марковского процесса удовлетворяет и второму уравнению Колмогорова

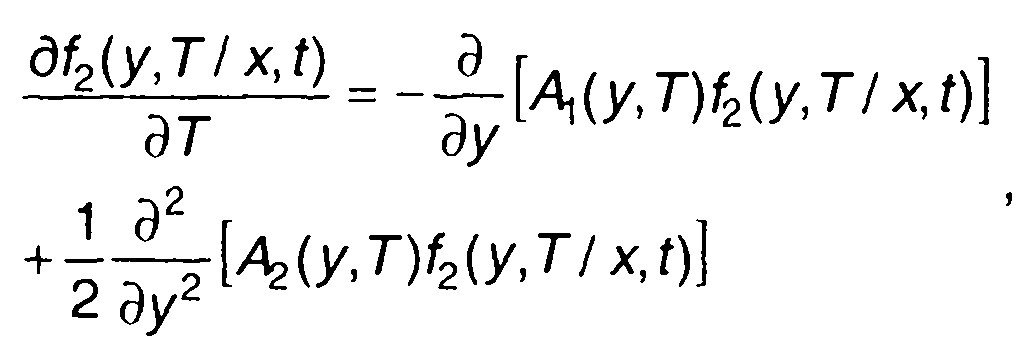(16.100)

Второе уравнение Колмогорова известно также как уравнение Фоккера-Планка.

При рассмотрении непрерывных случайных процессов исполь­зование марковской модели связано с определением шага по вре­менной оси: ∆t = t_n - t_n_₁. При ∆t →0 марковский процесс переходит в пуассоновский.

Раздел 17.

РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ И ИХ ФУНКЦИОНАЛЬНЫХ ПРЕОБРАЗОВАНИЙ

Характеристики распределения вероятностей, рассмотренные для одного случайного процесса, могут быть распространены на совокупность случайных процессов. В разделе рассматриваются характеристики распределения вероятностей нескольких случай­ных процессов, а также характеристики распределения вероятно­стей функций случайных процессов.

17.1. Совместное распределение вероятностей двух случайных процессов

Функция распределения вероятности двух случайных процессов ξ₁ (t) и ξ₂(t) определяется как

(17.1)

где Р{...} - символ вероятности.

Функция распределения вероятностей (п+т)-порядка зависит от (n+т) значений случайных процессов х₁, х₂,...,х_n, у₁, у₂,...,у_т, а также от моментов времени t₁, t₂,..., t_n, t₁, t₂,..., t_m, в которые рассматри­ваются случайные процессы. Для стационарных случайных про­цессов ФРВ зависит не от моментов времени, а от интервалов ме­жду ними.

Функции распределения вероятностей, определяемой (17.1), соответствует (n+т)-мерная ПРВ

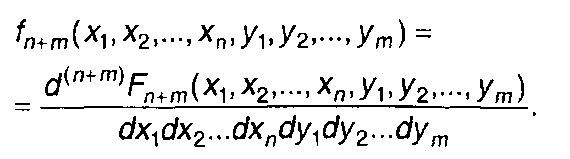(17.2)

Если ФРВ (ПРВ) двух случайных процессов может быть пред­ставлена в виде произведения ФРВ (ПРВ) каждой из них

(17.3)

при любом выборе моментов времени, то такие случайные процес­сы называются независимыми.

Моменты распределения вероятностей случайных процессов определяются выражениями:

начальные (порядка р = ∑k₁ +∑I₁)

(17.4)

центральные (того же порядка)

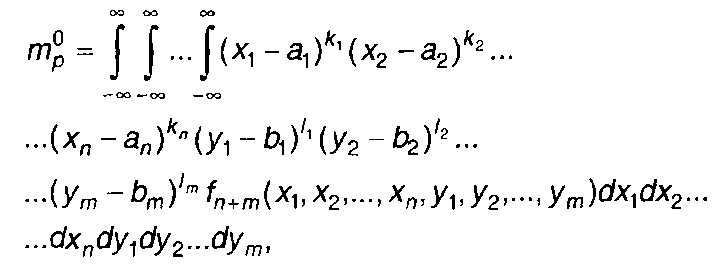(17.5)

где а_к, b_к- математические ожидания случайных процессов ξ₁(t) и ξ₂(t) в соответствующие моменты времени.

Для стационарных случайных процессов a₁ - а₂ =...= а_n = а, b₁ = b₂ =...= b_т = Ь.

Начальный момент второго порядка совместного распределе­ния вероятностей представляет ковариационную функцию случай­ных процессов

(17.6)

где f_ξ1ξ2(x, у) - двумерная ФРВ случайных процессов ξ₁(t) и ξ₂(t) Подчеркивая, что ковариационная функция определена для двух случайных процессов, ее называют взаимной ковариационной функцией.

Центральный момент распределения второго порядка пред­ставляет взаимную корреляционную функцию

(17.7)

где a, b - математические ожидания случайных процессов в мо­менты времени t₁ t₂.

Взаимная корреляционная функция стационарных случайных процессов (также, как и ковариационная функция) зависит не от моментов времени t₁ t₂, в которые рассматриваются случайные процессы, а от интервала между ними, т.е.

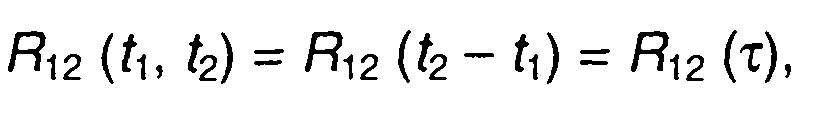
где τ=t₂-t₁.

Нормированная взаимная корреляционная функция стационар­ных случайных процессов определяется как

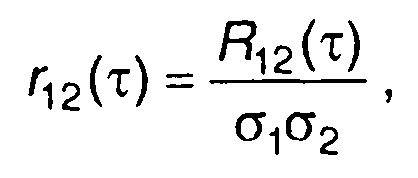(17.8)

где σ₁², σ₂² - дисперсии случайных процессов.

Если ξ₁(t), ξ₂(t)- независимые случайные процессы, то из (17.7) получим

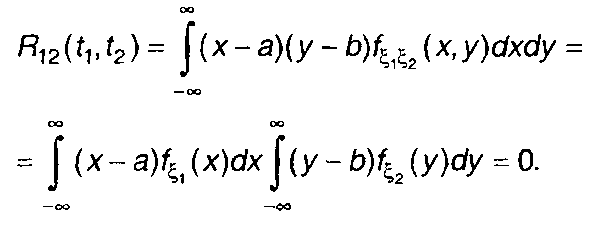(17.9)

Как следует из (17.9), корреляционная функция независимых случайных процессов равна нулю. Однако обратное утверждение неверно.

Взаимная корреляционная функция эргодических случайных процессов может быть определена как среднее по времени произ­ведения их реализаций

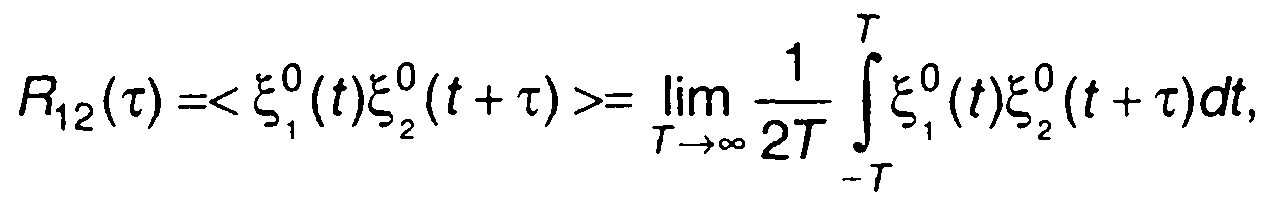(17.10)

где <...>- символ усреднения по времени.

Если задана (n + m)-мерная ПРВ случайных процессов ξ₁(t) и ξ₂(t) то может быть определена условная ПРВ - ПРВ совокупности

случайных величин ξ₁(t₁), ξ₁(t₂), ..., ξ₁(t_n), при условии, что случай­ные величины ξ₂(t₁), ξ₂(t₂), ..., ξ₂(t_m), принимают заданные значения У₁ ,У₂, ...,У_т

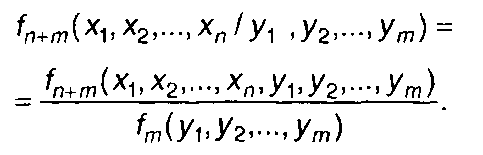(7.11)

Для независимых случайных процессов ξ₁(t) и ξ₂(t) из (17.11) по­лучим

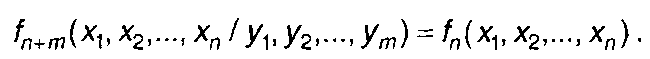(17.12)

Для нескольких случайных процессов могут быть определены и другие условные характеристики распределения аналогично то­му, как это было сделано для одного случайного процесса.

17.2. Распределение вероятностей функций случайных процессов

Ниже приводятся постановка и решение задачи нахождения ха­рактеристик распределения функций двух и более случайных ве­личин. Рассматриваемые случайные величины - это совокупность значений случайных процессов в выбранные моменты времени. Результаты такого анализа могут быть использованы при рассмот­рении преобразований случайных процессов в радиотехнических цепях различного вида.

17.2.1. Функция двух случайных величин

Рассмотрим случайные величины η₁ и η₂, определяемые как функции случайных величин ξ₁ и ξ₂

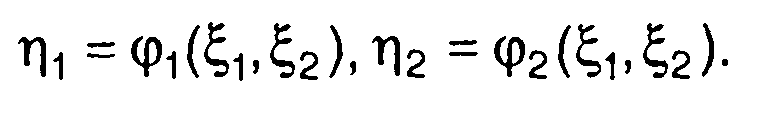(17.13)

Случайные величины ξ₁ и ξ₂ представляют значения двух слу­чайных процессов ξ₁(t) и ξ₂(t) в различные моменты времени: ξ₁= ξ₁(t₁) и ξ₂= ξ₂(t₂) Рассмотрение и выводы могут быть отнесены и к одному случайному процессу в различные моменты времени -

Зависимости, обратные (17.13), запишем в виде

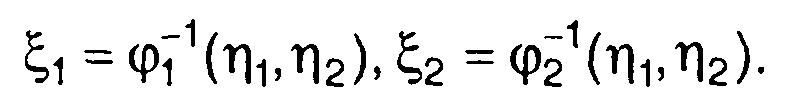(17.14)

Выражение для двумерной ПРВ случайных величин η₁ , η₂ име­ет вид

(17.15)

где fξ₂ (Х₁, Х₂), f_η2 (y1, y2) - двумерные ПРВ случайных величин ξ₁,ξ₂ и η₁,η₂;

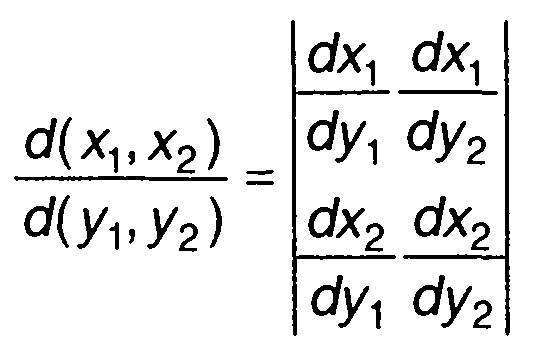(17.16)

- якобиан преобразования.

Выражение (17.15) записано для однозначных обратных зави­симостей (17.14). Для неоднозначных зависимостей необходимо произвести суммирование по числу обратных соотношений, по аналогии с тем, как это сделано при рассмотрении одного случай­ного процесса в разд. 15.

Часто встречается зависимость одной случайной величины от двух случайных величин

(17.17)

Чтобы получить характеристики распределения η в этом случае, рассмотрим прежде всего частный случай зависимости (17.17)

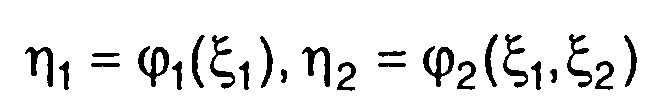(17.18)

при однозначных обратных зависимостях

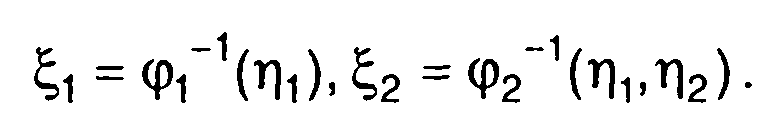(17.19)

Якобиан преобразования в этом случае равен

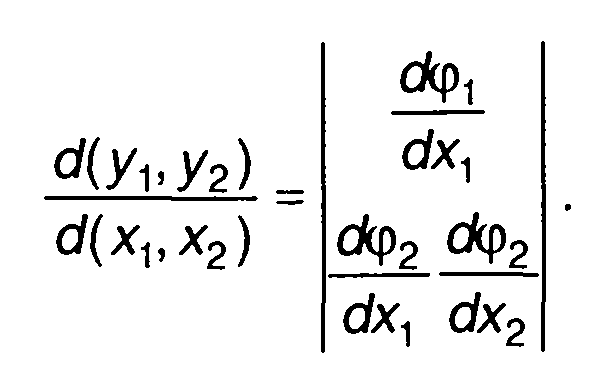(17.20)

В соответствии с (17.15) выражение для двумерной ПРВ запи­шется в виде

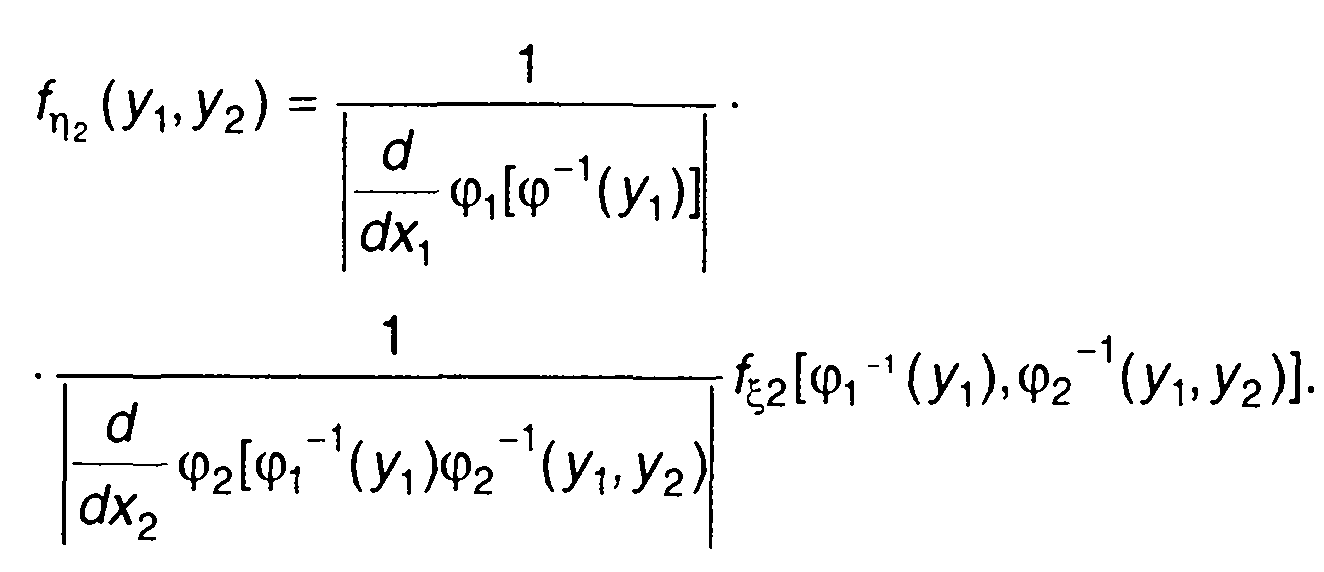(17.21)

Плотность распределения вероятностей одной случайной вели­чины η₂ определяется как

(17.22)

Подставляя (17.21) в (17.22) и вводя обозначение u = φ₁^-1(у₁), получим

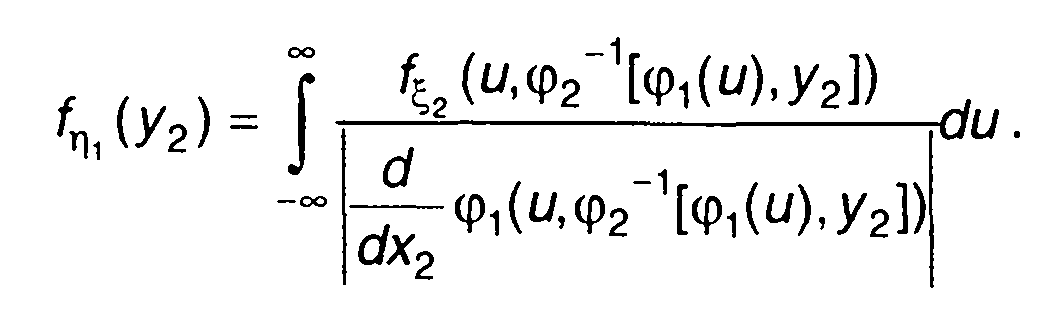(17.23)

Применительно к зависимости (17.18): η₁= ξ₁, φ1(х) = х, из

(17.23) найдем

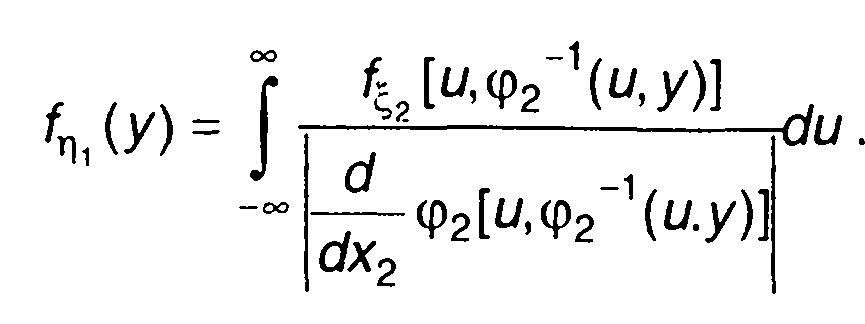(17.24)

Таким образом, записано выражение для плотности распреде­ления вероятности случайной величины, являющейся функцией двух случайных величин.

В общем случае, когда в результате функционального преобра­зования случайных величин ξ₁, ξ₂, ..., ξ_nполучается совокупность слу­чайных величин η₁, η₂, ..., η_n, выражение для ее ПРВ записывается в виде

(17.25)

где

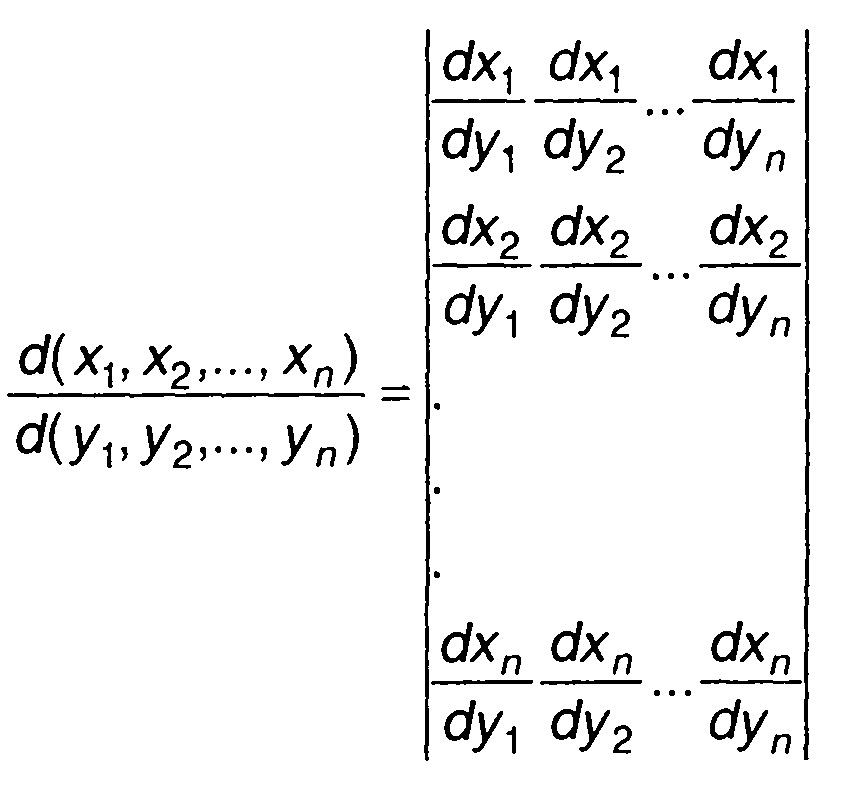(17.26)

- якобиан преобразования.

При неоднозначности обратных зависимостей в (17.25) необхо­димо произвести суммирование по их числу.

Если из совокупности n случайных величин ξ₁, ξ₂,..., ξ_n получается совокупность т случайных величин η₁, η₂,..., η_n, (т < n), то чтобы

воспользоваться (17.25), необходимо дополнить систему п - т функциональных зависимостей равенствами η_k = ξ_к, k = т + 1, т + 2,..., n. ПРВ случайных величин η₁, ri₂,...,η_n, получится из (17.25) интегрированием по у_{т + 1},..., у_n.

Моменты распределения вероятностей функции случайных ве­личин

(17.27)

определяются выражением

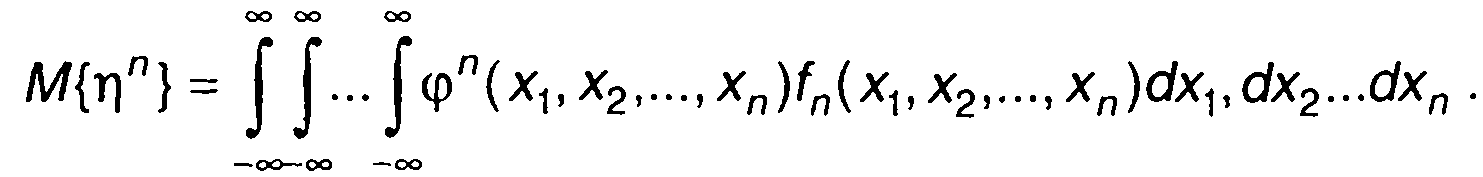(17.28)

При получении выражений для характеристик функций случай­ных величин говорилось о нескольких случайных процессах. Од­нако приведенные выражения справедливы и для функций значе­ний одного случайного процесса, взятых в различные моменты времени.

17.3. Некоторые виды функциональных преобразований случайных процессов

В качестве иллюстрации общего подхода к нахождению распре­деления случайного процесса, получающегося в результате преоб­разования, рассмотрим некоторые виды функциональных зависи­мостей. Выбранные примеры представляют и самостоятельный интерес, некоторые результаты используются в дальнейшем.

17.3.1. Сумма случайных величин

Для суммы (разности) двух случайных величин

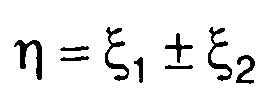(17.29)

имеем

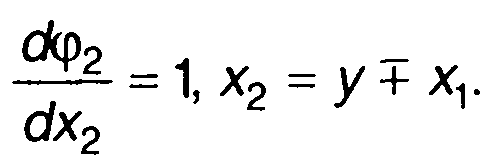(17.30)

С учетом (17.30) получим

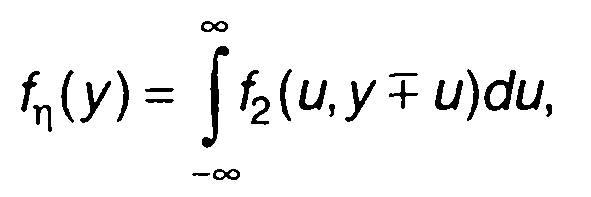(17.31)

где f₂ (х₁,х₂) - двумерная ПРВ случайных величин ξ₁,ξ₂.

Если случайные величины ξ₁,ξ₂ являются независимыми, (17.31) примет вид

(17.32)

где f_ξ1(х), f_ξ2 (х) - ПРВ случайных величин ξ₁ и ξ₂ .

Используя свойства преобразования Фурье, для суммы двух не­зависимых случайных величин получаем следующее выражение для характеристической функции

(17.33)

Вывод из полученного результата распространим на любую ко­нечную сумму случайных величин: характеристическая функция суммы независимых случайных величин

равна произведению характеристических функций каждой из них

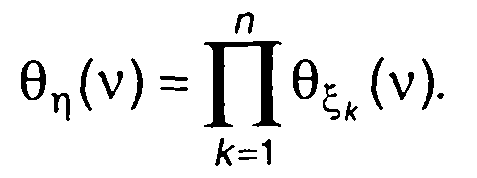(17.34)

Отмеченное свойство часто используется для получения ПРВ суммы независимых случайных величин - определяется характе­ристическая функция суммы (как произведение характеристических функций слагаемых), а от нее переходят к ПРВ. Пример такого подхода к определению ПРВ суммы независимых случайных вели­чин приведен в п.17.5.

Математическое ожидание η = ξ₁ ± ξ₂ определяется выраже­нием

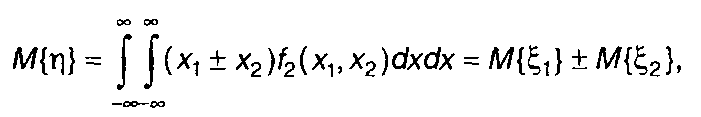(17.35)

где f₂ (х₁, х₂) - двумерная ПРВ ξ₁ и ξ₂.

Для n слагаемых запишем

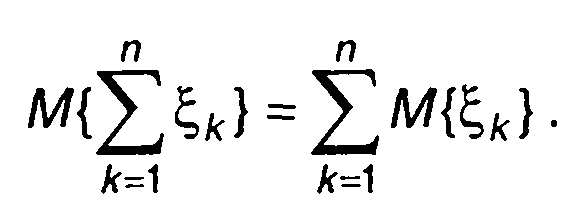(17.36)

Таким образом, математическое ожидание суммы случайных величин равно сумме математических ожиданий каждой из них.

Дисперсия суммы двух случайных величин определяется выра­жением

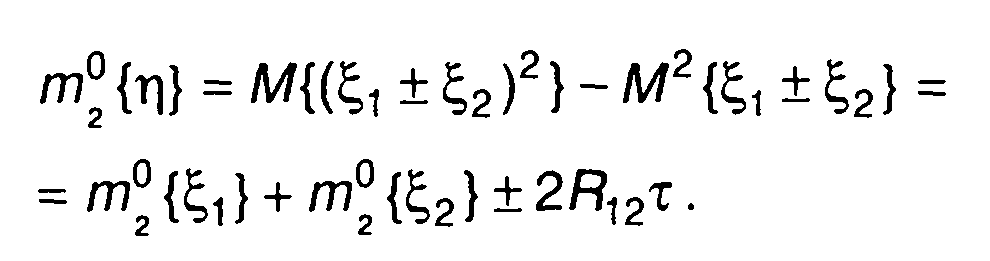(17.37)

Полученное выражение запишем в виде

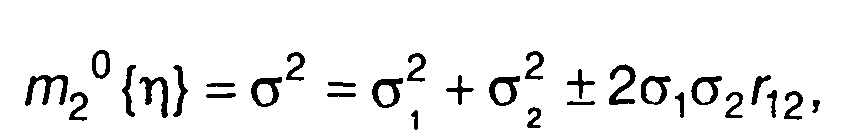(17.38)

где σ₁² ,σ₂² , r₁₂ - дисперсии случайных величин ξ₁ и ξ₂ и их норми­рованная взаимная корреляционная функция.

При г₁₂ (τ) =0 (ξ₁ и ξ₂ некоррелированные) из (17.38) получим

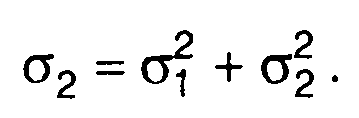(17.39)

Для суммы n некоррелированных случайных величин имеем

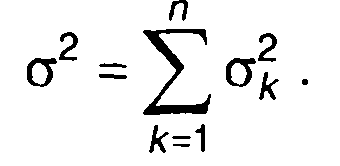(17.40)

Таким образом, дисперсия суммы некоррелированных случай­ных величин равна сумме их дисперсий.

Конкретизируем полученные результаты для некоторых видов распределений случайных величин.

1. Нормальное распределение

Для случайной величины

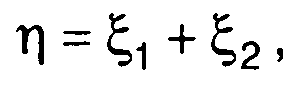
когда случайные величины ξ₁ и ξ₂ имеют нормальное распреде­ление

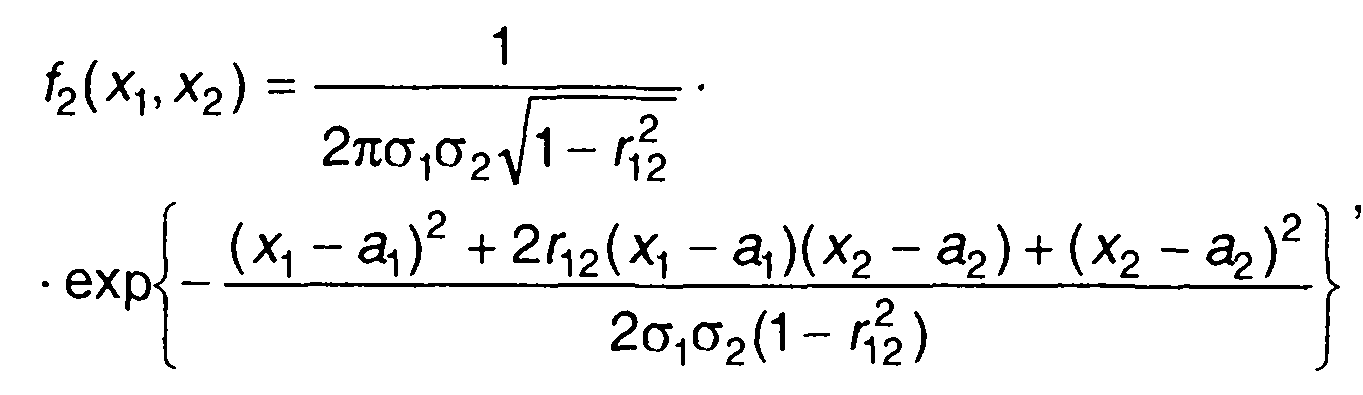(17.41)

где а₁, а₂, σ₁² ,σ₂² , г₁₂ - математические ожидания, дисперсии и нормированная корреляционная функция случайных величин ξ₁ , ξ₂ , из (17.31) получим

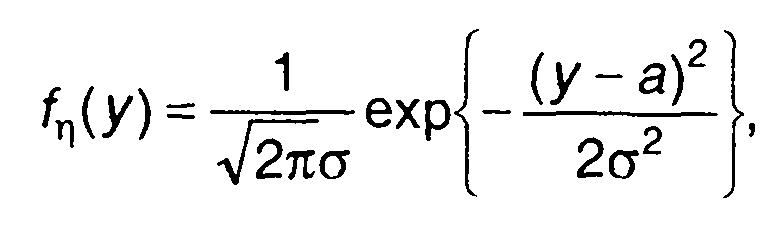(17.42)

где

(17.43)

Таким образом, сумма двух нормально распределенных слу­чайных величин имеет также нормальное распределение. С учетом того, что линейное преобразование не изменяет нор­мального закона распределения, сделанный вывод можно расши­рить: любая линейная комбинация нормальных случайных величин (гауссовских процессов) представляет собой нормальную случай­ную величину (гауссовский процесс).

Плотность распределения вероятностей гауссовского процесса любого порядка определяется математическим ожиданием и кор­реляционной функцией. Следовательно, чтобы определить ПРВ

случайного процесса, являющегося линейной комбинацией гаус­совских процессов, необходимо только определить математиче­ское ожидание и корреляционную функцию. Так для суммы двух гауссовских процессов

(17.44)

получим

(17.45)

(17.46)

где а₁,а₂, R₁(τ), R₂(τ) - математические ожидания и автокорреля­ционные функции случайных процессов ξ₁(t) иξ₂(t); R₁₂ (т) - взаим­ная корреляционная функция ξ₁(t) иξ₂(t).

2. Релеевское распределение

Плотность распределения вероятности суммы двух независи­мых случайных процессов, имеющих релеевское распределение с одним и тем же параметром а

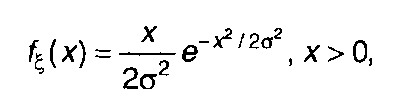(17.47)

определяется как

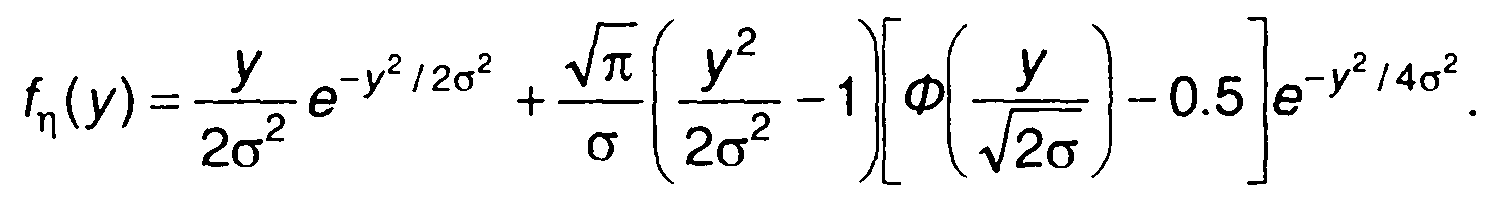(17.48)

3. Показательное распределение

Плотность распределения вероятностей случайных величин ξ₁ и ξ₂, имеющих показательное распределение, описываются выраже­ниями

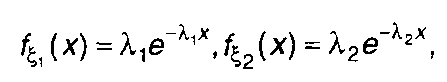(17.49)

где λ₁ и λ₂ - параметры распределения.

Для суммы η = ξ1 + ξ₂ , из (17.32) найдем

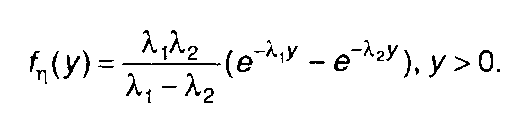(17.50)

Распространяя результат на сумму n случайных величин с

показательным распределением, можно получить

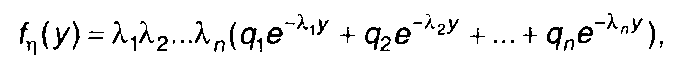(17.51)

где

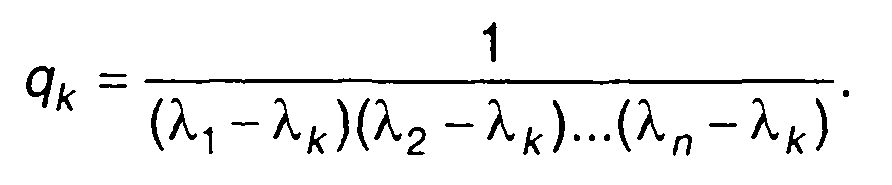
17.3.2. Произведение случайных величин

Для произведения двух случайных величин

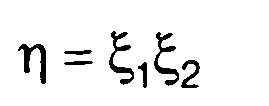(17.52)

в (17.24) имеем dφ₂/dx₂ = х₁, х₂ = у₂/х₁. Из (17.24) получим

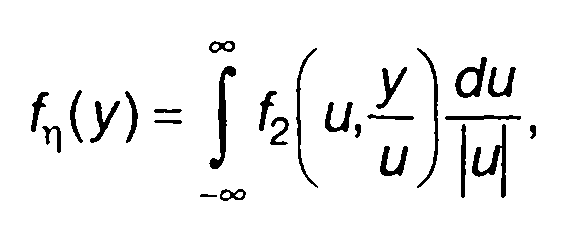(17.53)

где f₂ (х₁, х₂) - двумерная ПРВ случайных величин.

Если случайные величины ξ₁ иξ₂ являются независимыми,

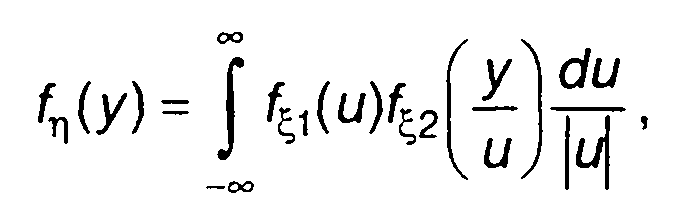(17.54)

где f_ξ1(х), f_ξ2 (х) - одномерные ПРВ случайных величин ξ₁ и ξ₂

Выражение для ПРВ произведения двух случайных величин конкретизируем для нормального и релеевского распределений.

1. Нормальное распределение

Двумерная ПРВ нормально распределенных случайных величин описывается (16.22). Подставляя (16.22) в (17.53), для произведе­ния двух центрированных случайных процессов получим

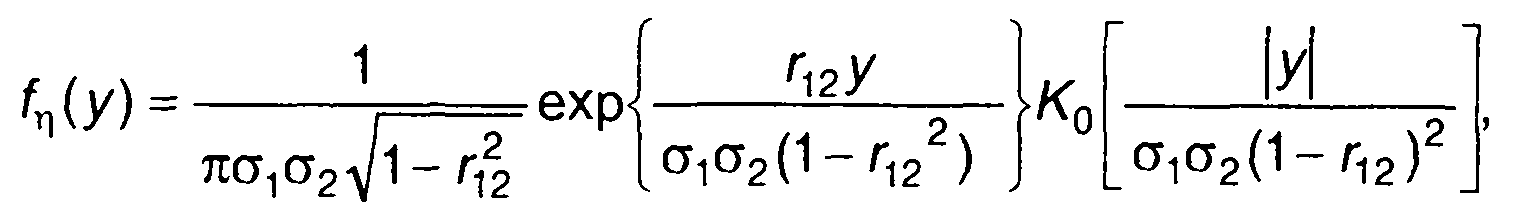(17.55)

где К₀ (х) - функция Бесселя второго рода.

Для некоррелированных случайных величин ξ₁ и ξ₂ (г₁₂ = 0)

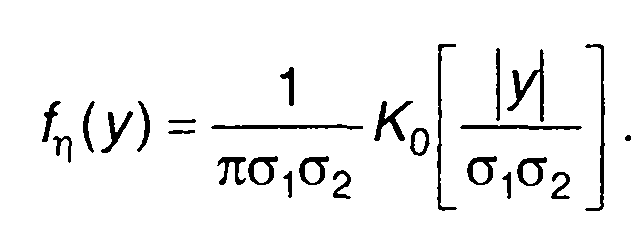(17.56)

2. Релеевское распределение

Плотность распределения вероятности произведения двух не­зависимых релеевских процессов с одним и тем же параметром может быть получена из (17.53) с подстановкой в него (17.47)

(17.57)

17.3.3. Частное случайных величин

Для частного случайных величин

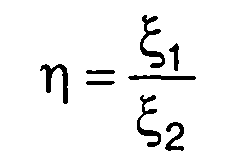(17.58)

(17.24) запишется в виде

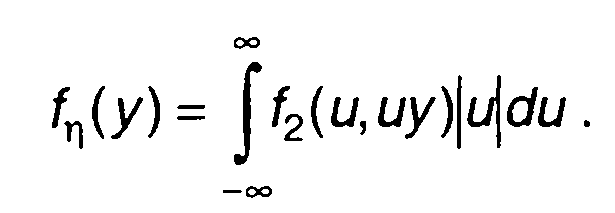(17.59)

Для независимых ξ₁ и ξ₂

(17.60)

При нормальном распределении случайных величин, имеющих математические ожидания, равные нулю, для их частного получим

(17.61)

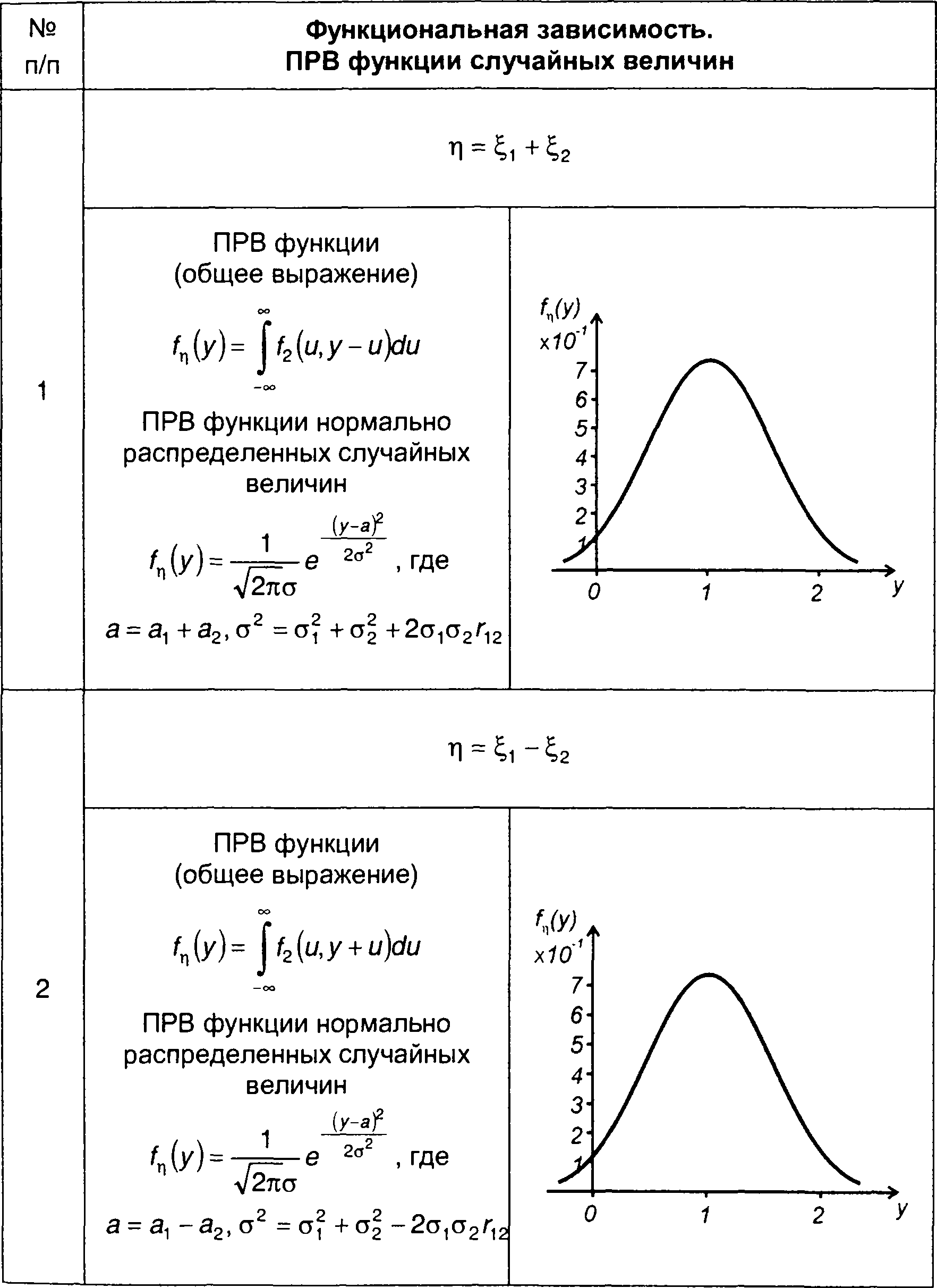
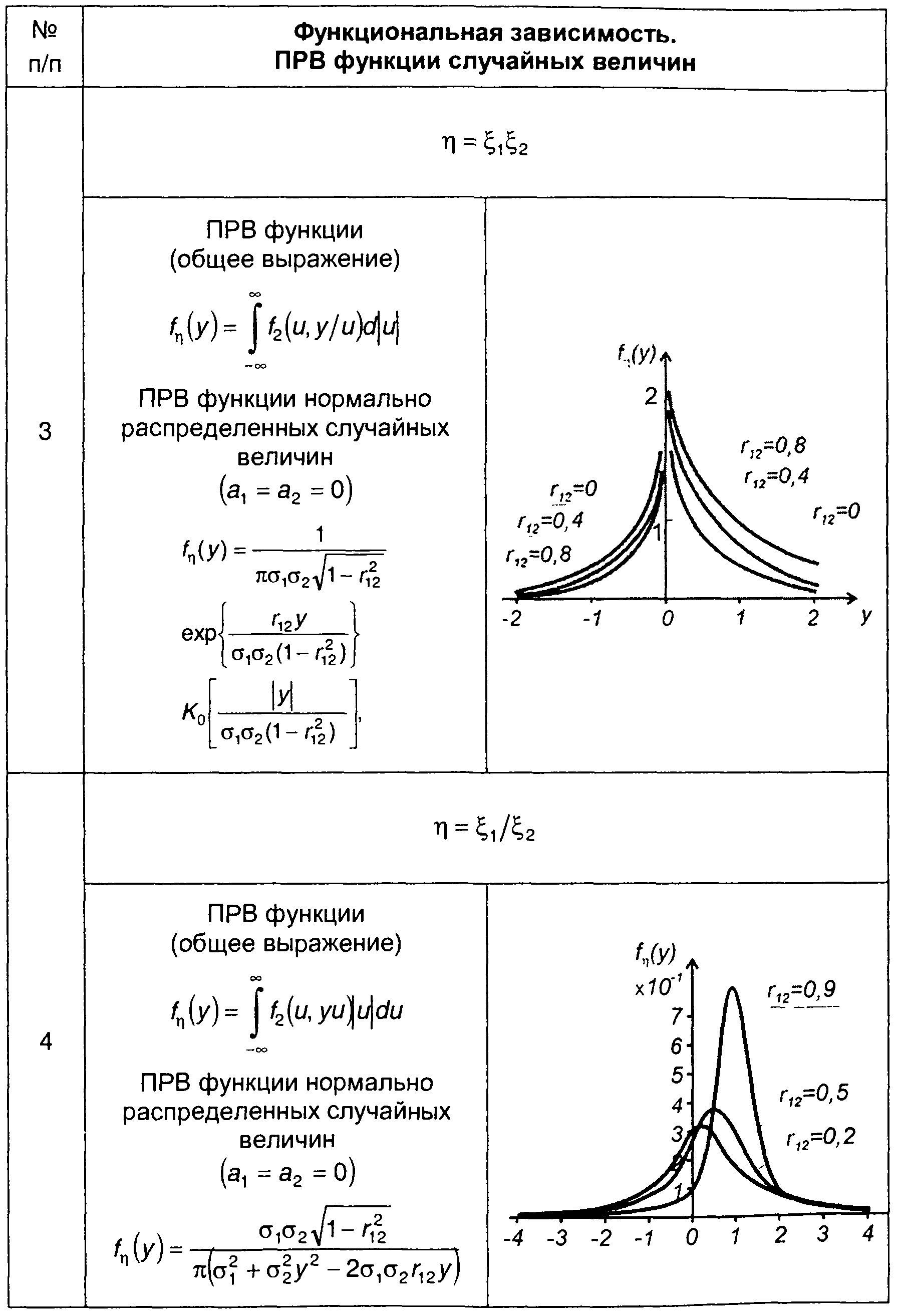
Выражения для ПРВ рассмотренных функций двух случайных величин и их графики при нормальном распределении случайных величин сведены в табл. 17.1.

Таблица 17.1.

Распределение функций двух случайных величин

17.4. Распределение вероятностей производной случайного процесса

Характеристики распределения вероятностей производной слу­чайного процесса могут быть получены, исходя из определения производной

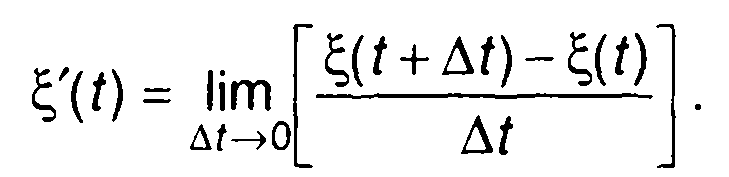(17.62)

Математическое ожидание производной равно

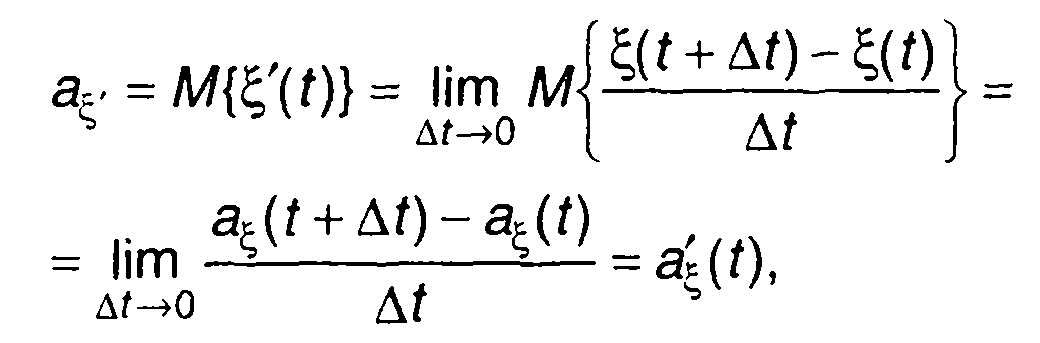(17.63)

где a_ξ (t) - математическое ожидание случайного процесса ξ(t) в момент времени t.

Таким образом, математическое ожидание производной слу­чайного процесса равно производной математического ожидания случайного процесса в рассматриваемый период времени. При этом предполагается, что случайный процесс в этой точке диффе­ренцируем. Если случайный процесс является стационарным, его математическое ожидание постоянно, не зависит от времени: ма­тематическое ожидание производной случайного процесса равно нулю.

Корреляционная функция производной центрированного слу­чайного процесса определяется выражением

(17.64)

Чтобы определить корреляционную функцию производной слу­чайного процесса, сначала запишем выражение для корреляцион­ной функции разности ξ(t-∆t) - ξ(t).

(17.65)

Представим (17.65) в виде

(17.66)

Разложим первые три слагаемых в правой части (17.66) в ряд Тейлора

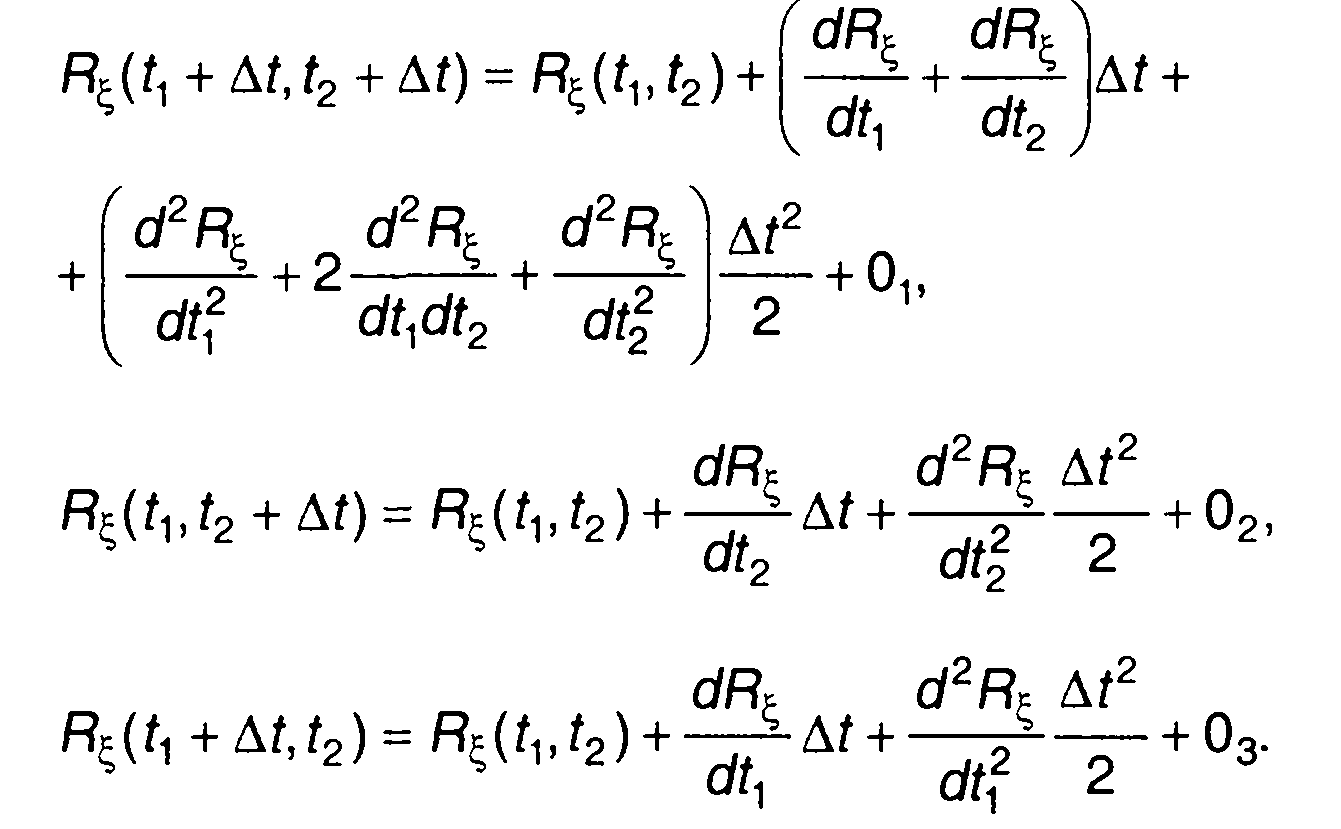(17.67)

Подставляя (17.67) в (17.66), получим

(17.68)

Из (17.64) с учетом (17.68) найдем

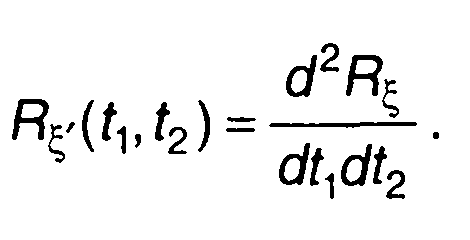(17.69)

Корреляционная функция стационарного случайного процесса зависит от разности моментов времени τ = t₂ - t₁. Для нее получим

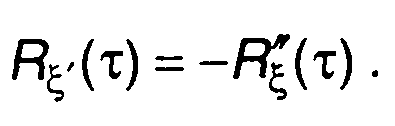(17.70)

Таким образом, корреляционная функция производной стацио­нарного случайного процесса равна второй производной корреля­ционной функции случайного процесса, взятой со знаком минус.

Корреляционная функция n-ной производной стационарного случайного процесса равна

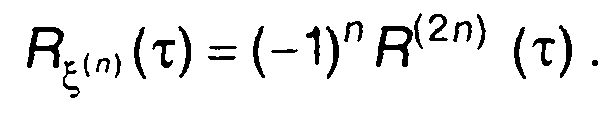(17.71)

Так же можно показать, что взаимная корреляционная функция n-ой и k-ой производных стационарного случайного процесса опре­деляется как

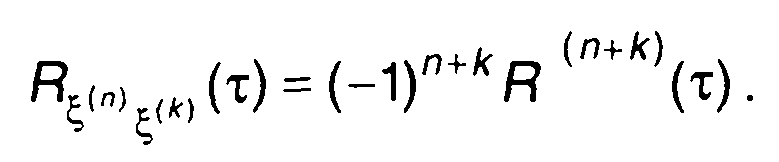(17.72)

Исходное выражение для определения взаимной корреляцион­ной функции случайного процесса и его производной записывается в виде

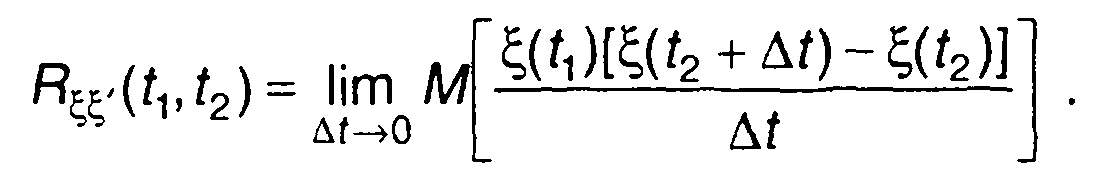(17.73)

Аналогично тому, как это было сделано раньше, предваритель­но рассмотрим взаимную корреляционную функцию случайного процесса ξ(t1) и разности ξ(t₂ + ∆t) - ξ(t₂):

(17.74)

Раскладывая первое слагаемое правой части (17.74) в ряд Тей­лора, запишем

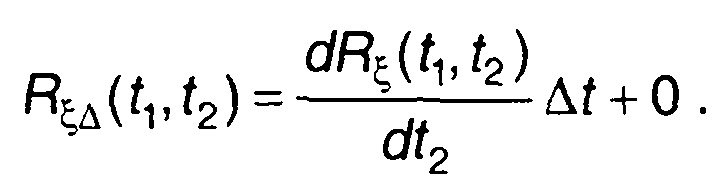(17.75)

С учетом (17.74) выражение для взаимной корреляционной функции случайного процесса и его производной получим в виде

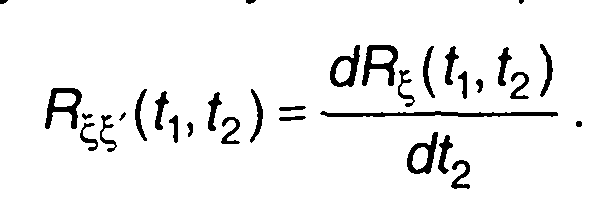(17.76)