ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 21 страница

Как следует из (19.16), V_c(t) и V_s(t) линейно связаны с Если ξ(t) представляет центрированный гауссовский процесс, то и V_c(t) и V_s(t) являются также гауссовскими процессами с математическими ожида­ниями, равными нулю. Вторые моменты распределения равны:

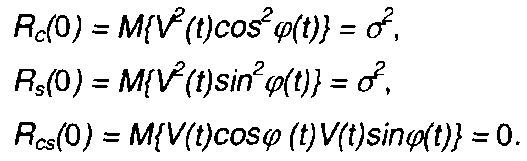
Для гауссовских процессов равенство нулю корреляционной функции означает независимость. Таким образом, совместная ПРВ V_c(t) и V_s(t) равна произведению их одномерных ПРВ:

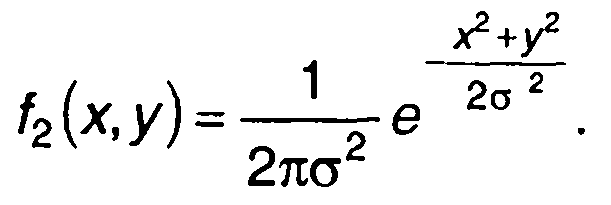(19.18)

Квадратурные составляющие V_c(t) и V_s(t) связаны с огибающей и фазой случайного процесса выражениями (19.17). Переход от V_c(t) и V_s(t) к огибающей и фазе устанавливается соотношением (раздел 17)

(19.19)

где f_Vφ2(p, θ) - двумерная ПРВ огибающей и фазы.

Такой переход аналогичен преобразованию прямоугольных ко­ординат в полярные. Из (19.19) с учетом (19.18) получим

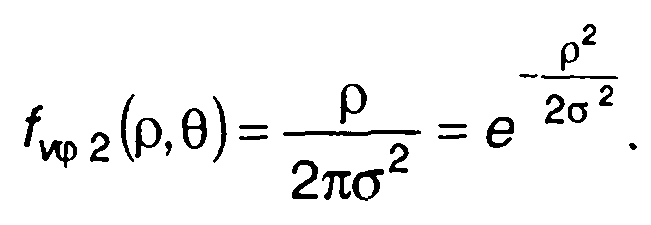(19.20)

Плотность распределения вероятностей огибающей найдется из (19.20) как (рис. 19.11)

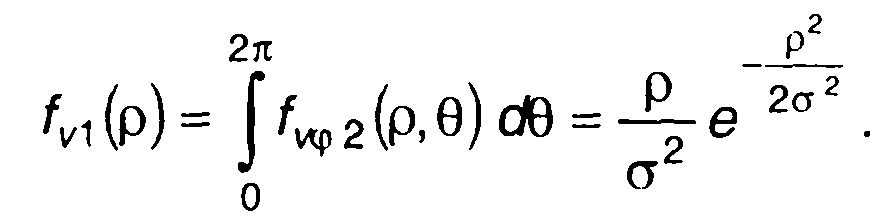(19.21)

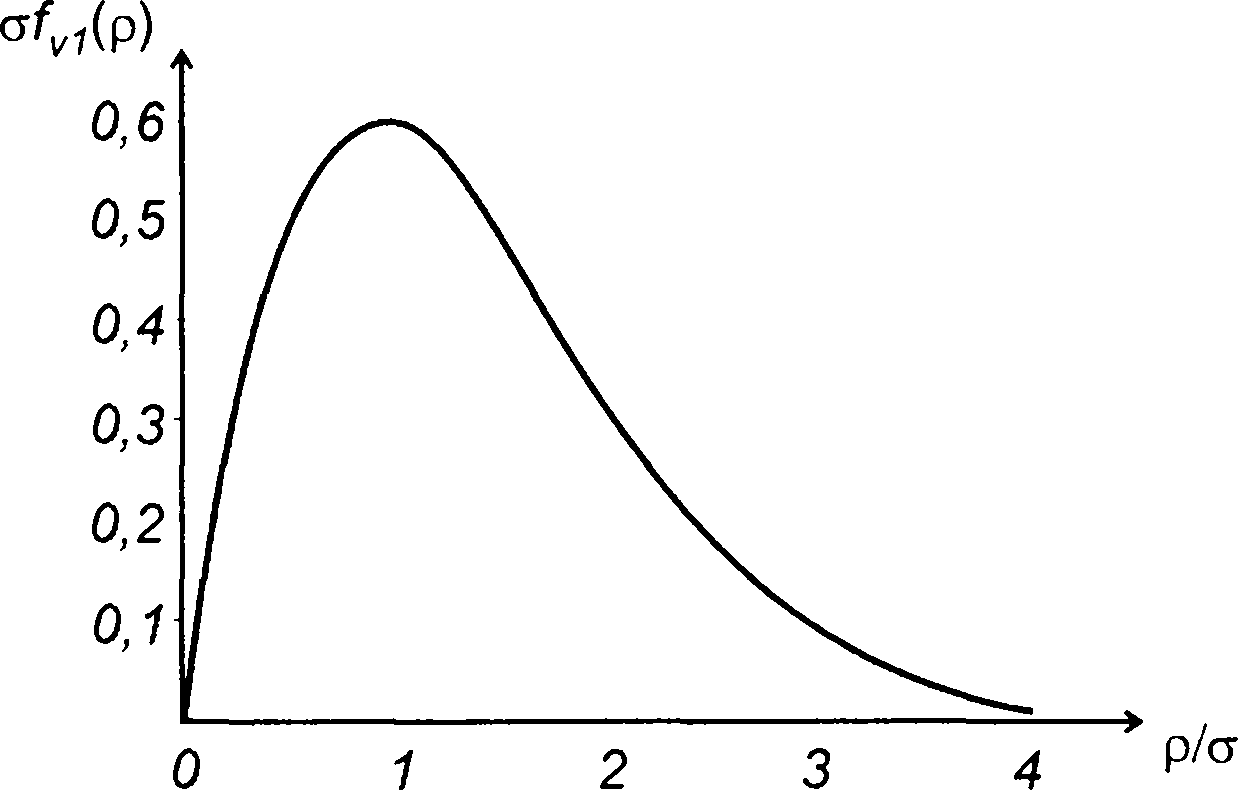
Рис. 19.11

Таким образом, распределение огибающей узкополосного слу­чайного процесса подчиняется закону Релея (разд. 15).

Плотность распределения вероятностей фазы

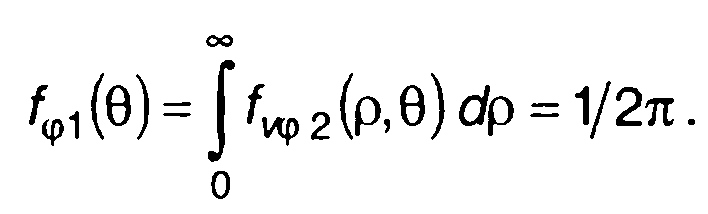(19.22)

Как следует из (19.22), ПРВ фазы является равномерной на ин­тервале [0, 2π]. Огибающая и фаза узкополосного гауссовского процесса в каждый момент времени являются независимыми.

19.3. Распределение огибающей и фазы смеси сигнала и шума

Рассмотрим смесь узкополосного гауссовского процесса (шума) ξ(t) и гармонического колебания (сигнала) s(t)] частота сигнала совпадает со средней частотой случайного процесса

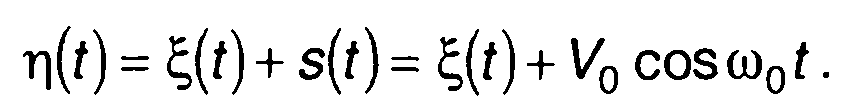(19.23)

С учетом (19.1) запишем

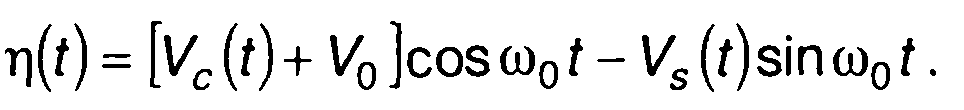(19.24)

Как узкополосный случайный процесс η(t) представим в виде

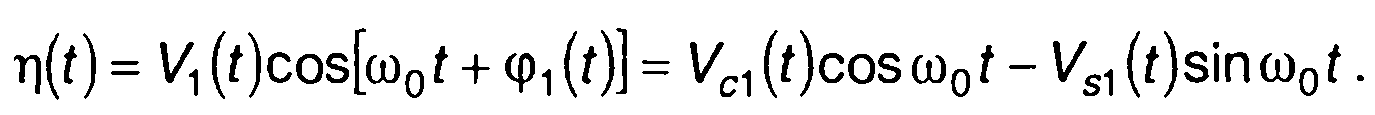(19.25)

В (19.25)

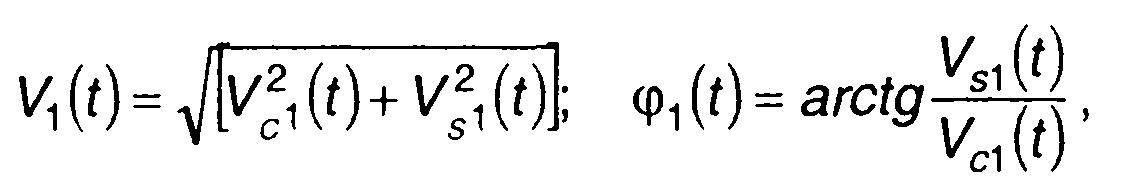(19.26)

где V_c1(t)=V_c(t)+V₀ , V_s1(t) =V_s(t).

Совместная ПРВ составляющих V_c1(t) и V_s1(t) равна

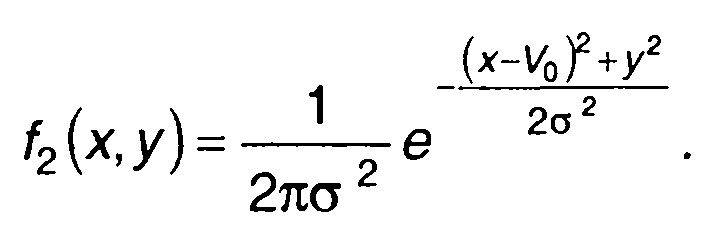(19.27)

Переход к огибающей и фазе выполняется, как показано в § 19.2,

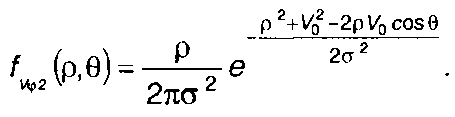(19.28)

Из (19.28) следует, что огибающая и фаза в рассматриваемом случае являются зависимыми величинами. Наличие в показателе степени члена, содержащего pcosθ не позволяет представить f_vφ2(p,θ) как произведение f_v1(p) и f_φ1(θ).

Плотность распределения вероятностей огибающей определим как и раньше, интегрированием (19.28) по θ

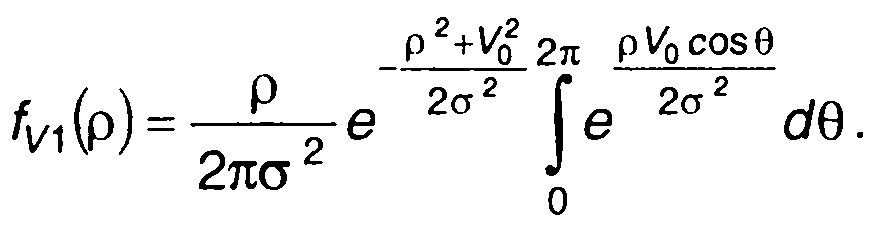(19.29)

Из (19.29) получим (рис. 19.12)

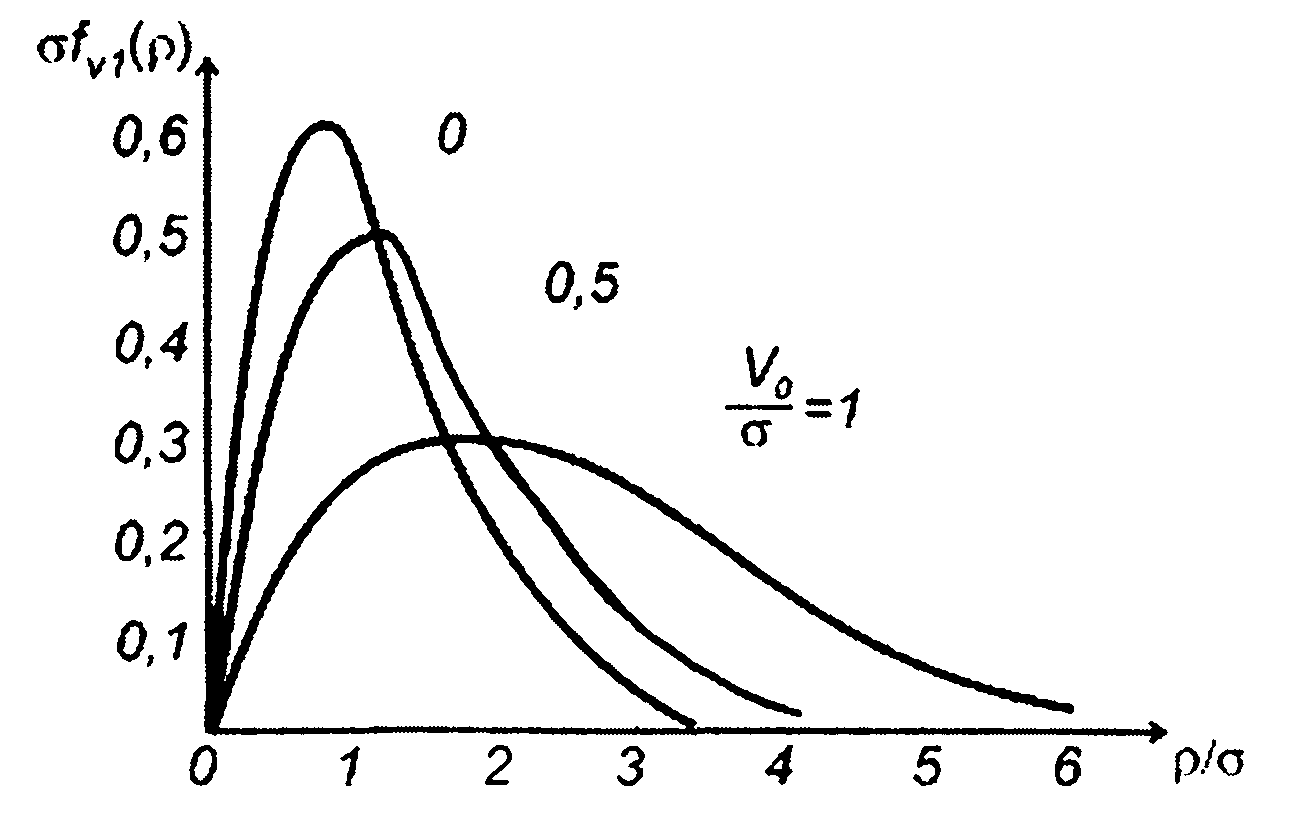
Рис.19.12

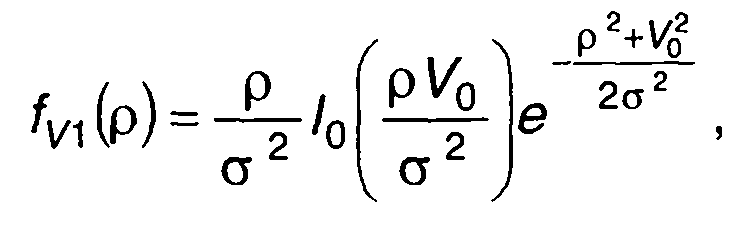(19.30)

где l₀(x) - модифицированная функция Бесселя первого рода ну­левого порядка.

Таким образом, распределение огибающей смеси узкополосно­го гауссовского процесса и гармонического сигнала подчиняется обобщенному закону Релея (разд. 15).

Плотность распределения вероятностей фазы описывается вы­ражением (получено с учетом (19.28)) [26].

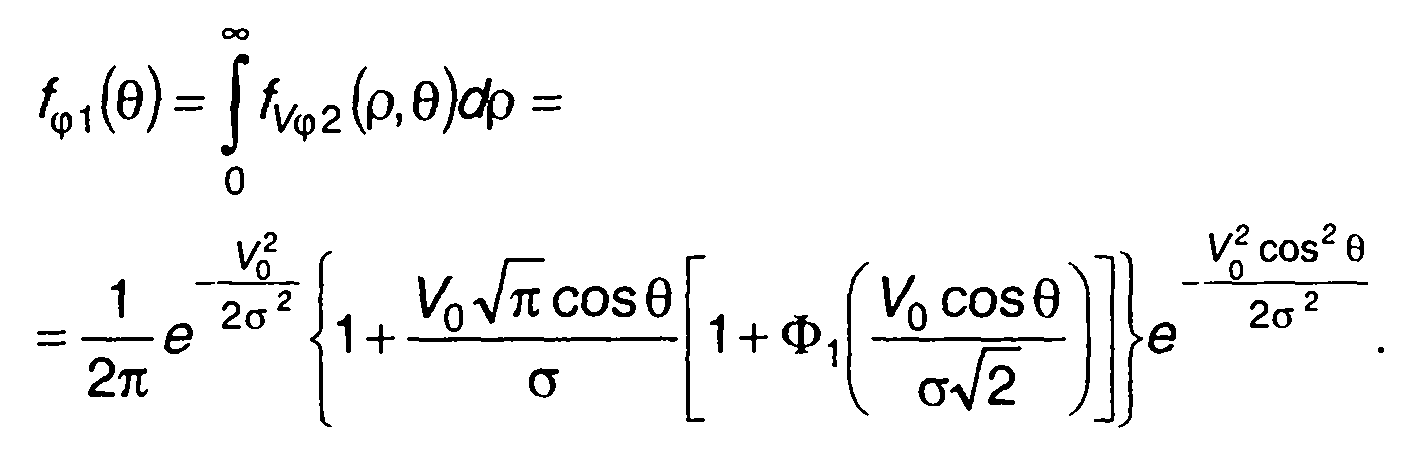(19.31)

При

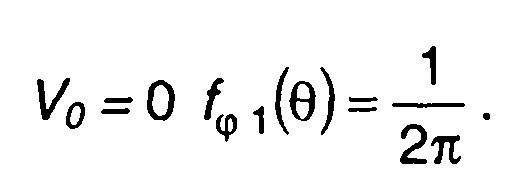(19.32)

19.4. Модулированные случайные процессы

Узкополосными случайными процессами часто являются моду­лированные колебания. Модулированное колебание представляет высокочастотное колебание (несущее), на которое наложено низ­кочастотное - модулирующее (содержащее передаваемую инфор­мацию). Наибольшая частота спектра модулирующего колебания значительно меньше частоты несущего колебания. Это условие и определяет узкополосность модулированного колебания.

Случайные процессы могут служить в качестве несущего или модулирующего колебания. Случайный процесс как несущее коле­бание является узкополосным, на него накладывается низкочас­тотный сигнал (детерминированный или случайный). В качестве модулирующего случайный процесс, как правило, используется при модуляции гармонического колебания. Этот случай наиболее рас­пространенный, он и рассматривается в разделе - модуляции слу­чайным процессом гармонического колебания.

Модулируется несущее колебание путем изменения одного или нескольких его параметров. В зависимости от изменяемого пара­метра различают и вид модуляции. Ниже рассматриваются коле­бания с амплитудой и угловой (фазовой и частотой) модуляцией.

19.5. Случайный процесс с амплитудной модуляцией

Случайный процесс с амплитудной модуляцией (AM), как пра­вило, является узкополосным и при обычной AM может быть пред­ставлен в виде (рис. 19.13)

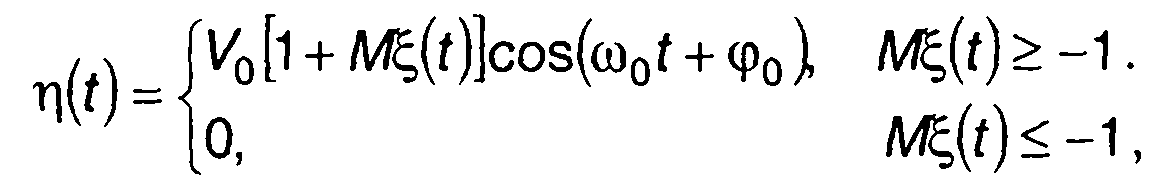(19.34)

где V₀, ω₀, φ₀ - амплитуда, частота и начальная фаза несущего ко­лебания; ξ(t) - модулирующий случайный процесс; М - коэффици­ент модуляции.

Обращение η(t) в нуль при Mξ(t) ≤ -1 означает перемодуляцию. При AM детерминированным сигналом перемодуляция возникает только при соответствующем выборе коэффициента модуляции. Когда модулирующее колебание представляет случайный процесс с неограниченным распределением его значений, всегда будет иметь место перемодуляция. Если модулирующий случайный про­цесс ξ(t) имеет ПРВ f_ξ1(x) , то вероятность превышения уровня - 1/М что соответствует перемодуляции) будет равна

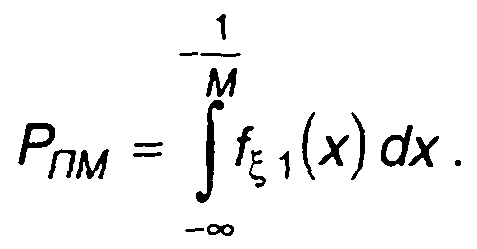(19.35)

Значение Р_пм определяет ту относительную часть времени, ко­гда происходит перемодуляция несущего колебания.

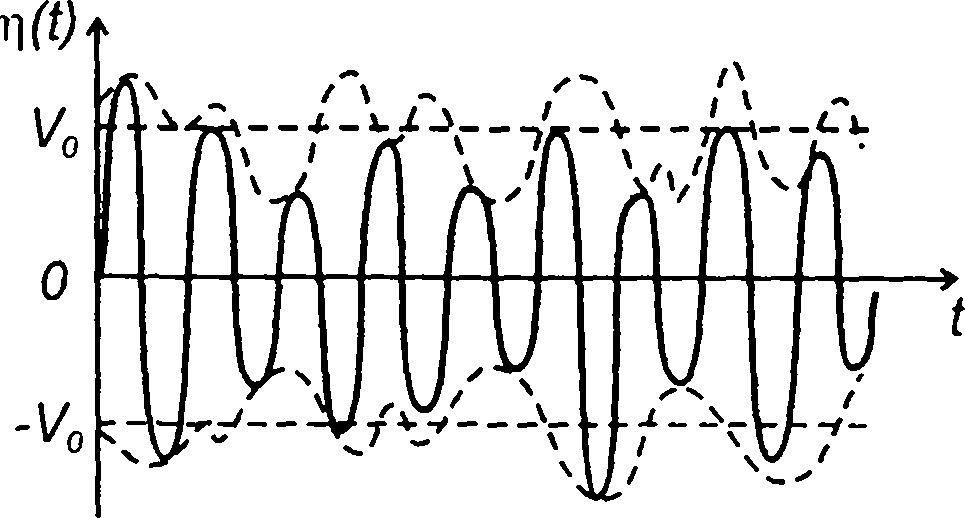
Рис. 19.13

При нормальном распределении модулирующего случайного процесса из (19.35) получим

где 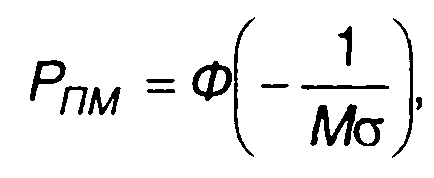(19.36)

С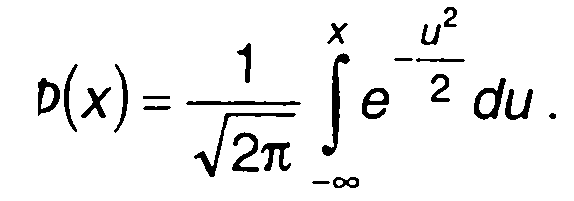

Основными характеристиками модулированного случайного процесса η(t) являются корреляционная функция и спектральная плотность мощности. Корреляционная функция случайного про­цесса определяется как

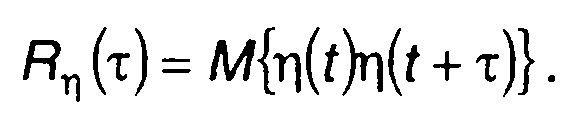(19.37)

Если перемодуляцией можно пренебречь, то с учетом (19.34) из (19.37) получим

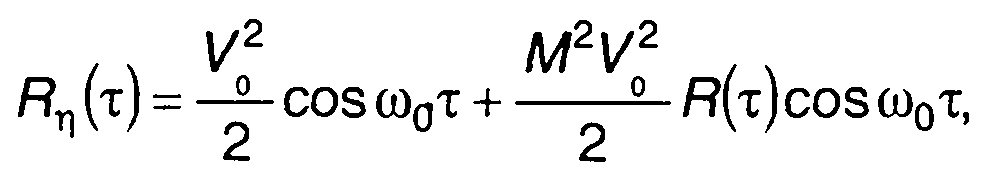(19.38)

где R(t) - корреляционная функция модулирующего случайного процесса.

Спектральная плотность мощности AM случайного процесса определяется как преобразование Фурье (19.38)

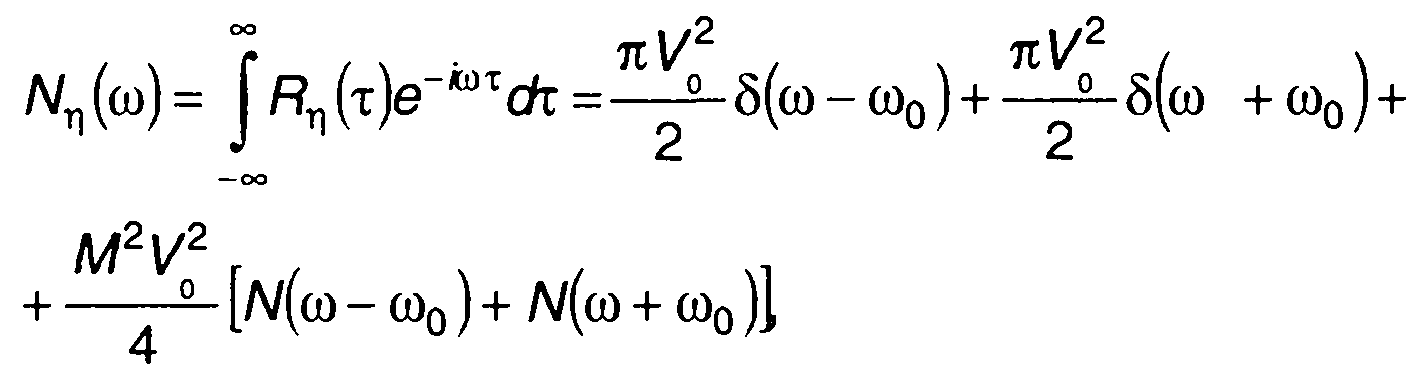(19.39)

где N(ω) - спектральная плотность мощности модулирующего слу­чайного процесса.

В (19.39) первые два слагаемых представляют импульсные функции на частотах ±ω₀ площадью πV²₀/2; вторые два описывают непрерывную часть спектра в области положительных и отрица­тельных частот - около частот ±ω₀ (рис. 19.14). Таким образом, спектр AM случайного процесса получается наложением на дис­кретную составляющую с частотой ±ω₀ спектра модулирующего случайного процесса (с соответствующим коэффициентом). Однако

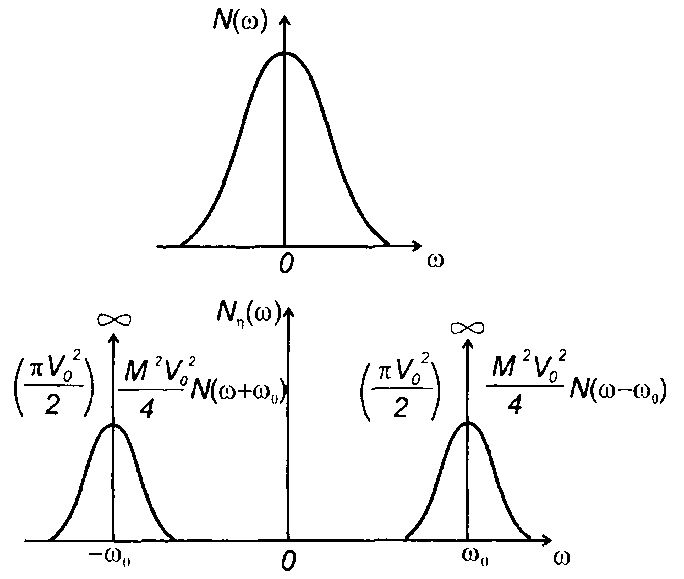
Рис. 19.14

преобразование спектра случайного процесса при AM как линейное можно рассматривать только тогда, когда перемодуляцией можно пренебречь.

Средняя мощность AM случайного процесса равна R_η(0)

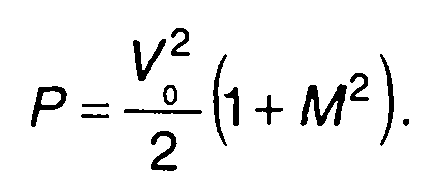(19.40)

Мощность несущего колебания -

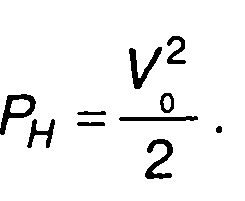(19.41)

В качестве примеров рассмотрим различные виды модулирую­щих случайных процессов.

1 .Спектральная плотность мощности и корреляционная функция модулирующего случайного процесса (табл.18.1, п.1)

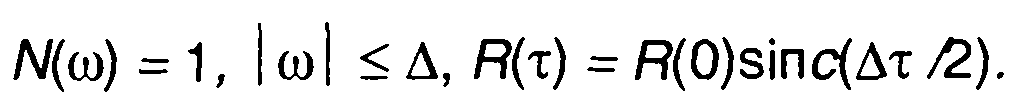
Корреляционная функция модулированного случайного процесса

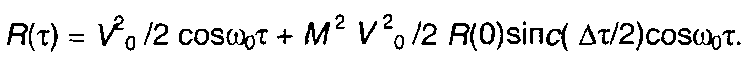
Спектральная плотность мощности модулированного случайно­го процесса в области положительных частот (рис. 19.15)

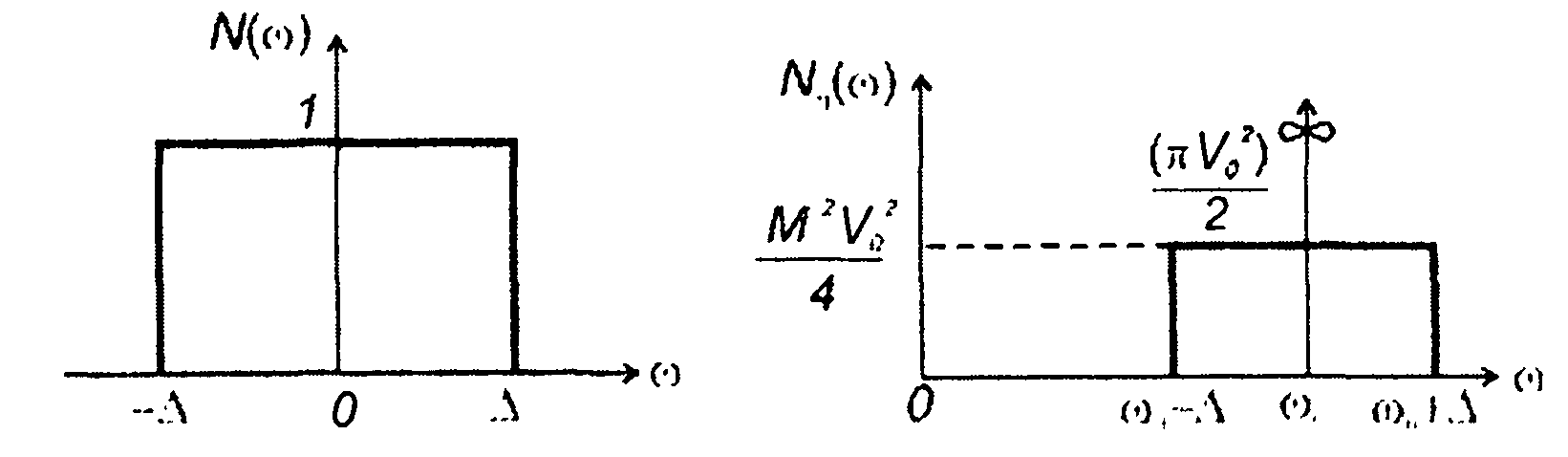
Рис. 19.15

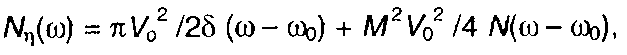
где N(ω - ω₀) = 1, |ω - ω₀I < ∆.

2. Спектральная плотность мощности и корреляционная функ­ция модулирующего случайного процесса (табл.18.1, п.З)

Корреляционная функция модулированного случайного процесса

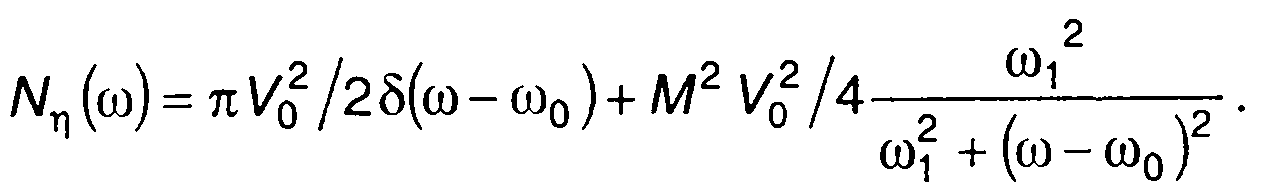
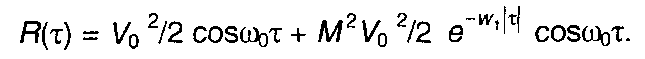
Спектральная плотность мощности модулированного случайно­го процесса в области положительных частот (рис. 19.16)

3. Спектральная плотность мощности и корреляционная функ­ция модулирующего случайного процесса (табл. 18.1, п.13)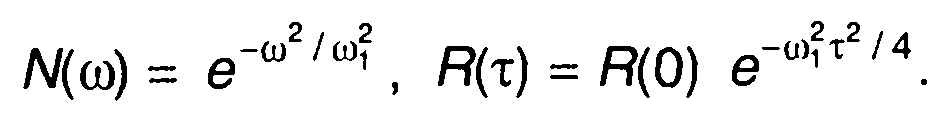

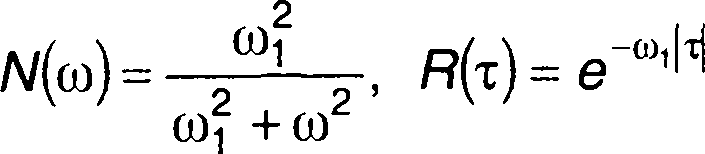
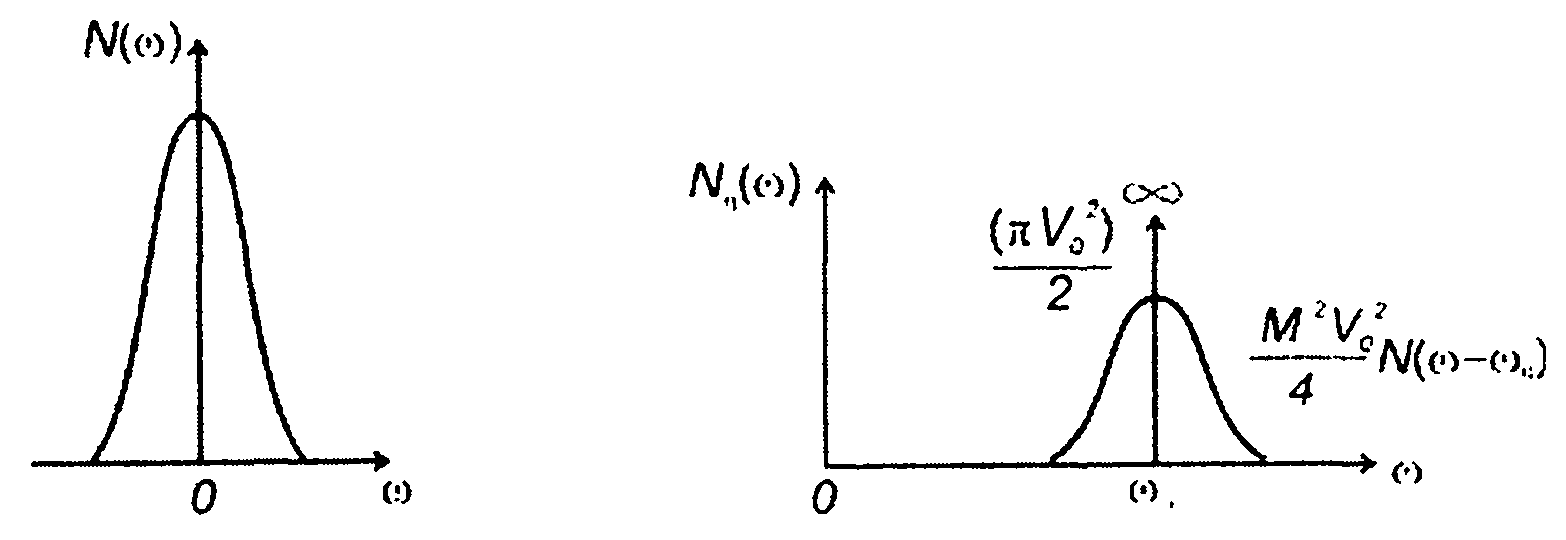
Рис. 19.16

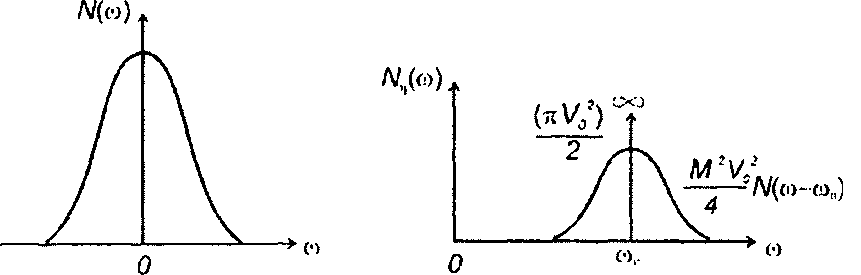
Рис. 19.17

Корреляционная функция модулированного случайного процесса

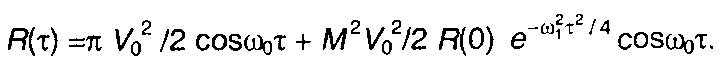
Спектральная плотность мощности модулированного случайно­го процесса в области положительных частот (рис. 19.17)

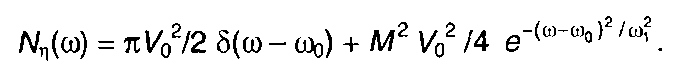
Когда перемодуляцией нельзя пренебречь, характеристики мо­дулированного случайного процесса можно найти, используя мето­ды анализа случайных процессов при нелинейных преобразовани­ях (разд. 22).

Если модулирующий случайный процесс выходит за пределы линейного участка модуляционной характеристики (результатом этого нельзя пренебречь), выражение для AM случайного процесса принимает вид

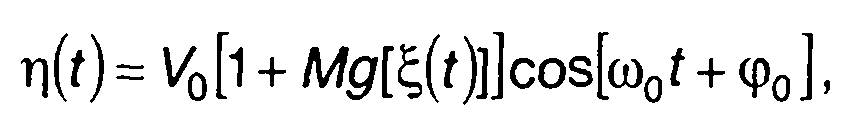(19.42)

где g(х) - функция, описывающая искажения модулирующего слу­чайного процесса.

Обычно модуляционную характеристику можно аппроксимиро­вать линейно-ломанной кривой. Для нее преобразование Лапласа имеет вид 1/iv (разд. 22). Выражение для AM случайного процесса в этом случае можно записать в виде

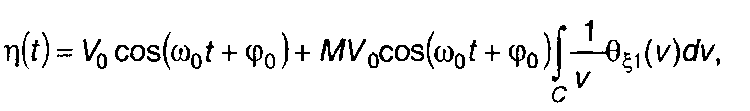(19.43)

где С - контур интегрирования.

Корреляционная функция η(t) определяется выражением

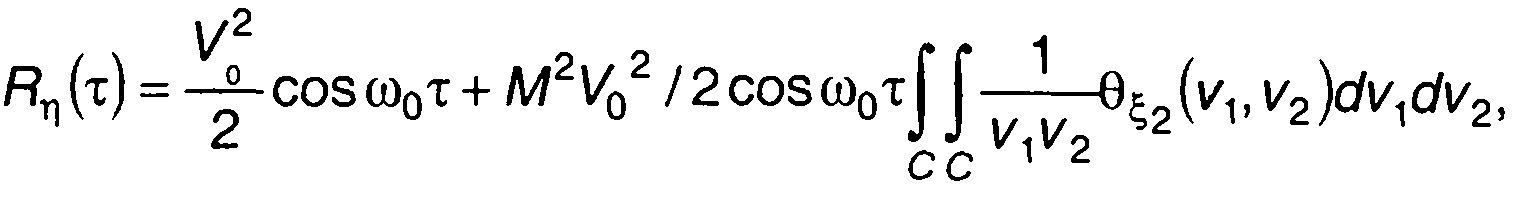(19.44)

гдеθ_ξ2 (v₁,v₂) - характеристическая функция ξ(t).

Решение (19.44) получено в виде ряда [19]:

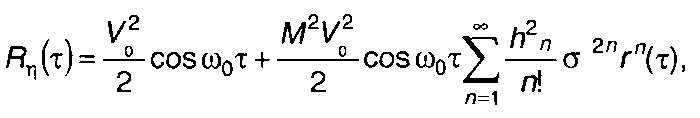(19.45)

где σ², r(τ) - дисперсия и нормированная корреляционная функция модулирующего случайного процесса.

Коэффициенты h_n определяются выражением

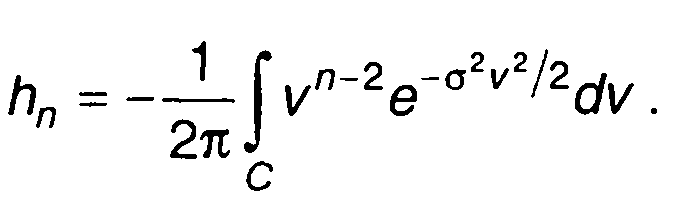(19.46)

Как указывалось, перемодуляцию можно не учитывать при σ <<1 /М. В этом случае выражение Rη(τ) примет вид

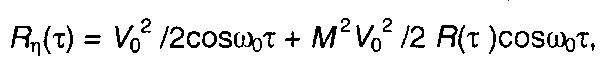(19.47)

что совпадает с (19.38)

Спектр модулированного случайного процесса определяется преобразованием Фурье

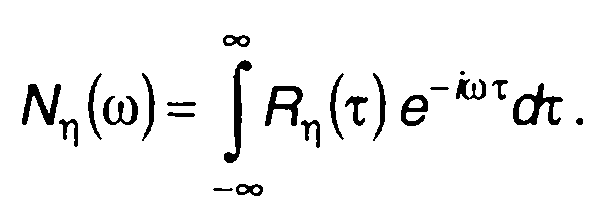(19.48)

Для ω>0 можем записать

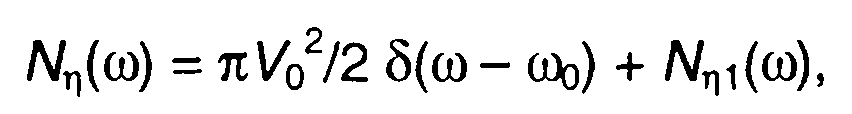(19.49)

где описывает непрерывную часть спектра, соответствую­щую второму слагаемому в (19.45) или (19.47).

Графики спектра модулированного случайного процесса при спектральной плотности мощности модулирующего случайного процесса

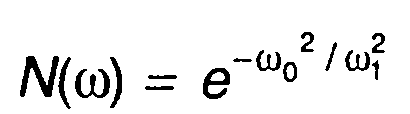(19.50)

приведены на рис. 19.18 [19]. Там же изображен спектр модулиро­ванного случайного процесса, полученный без учета перемодуля- ции (кривая, выполненная пунктиром). Сравнение приведенных кривых показывает определенное расширение спектра модулиро­ванного колебания при перемодуляции.

Амплитудно-модулированный случайный процесс при баланс­ной модуляции описывается выражением (часть 1)

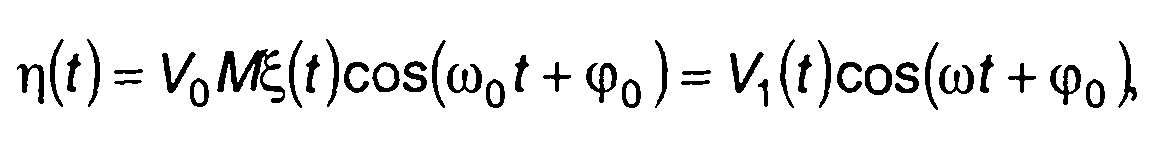(19.51)

где ξ(t) - модулирующий случайный процесс.

Корреляционная функция модулированного случайного процес­са равна

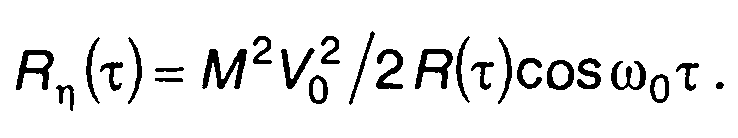(19.52)

Преобразование Фурье (19.52) дает спектральную плотность мощности (при ω > 0)

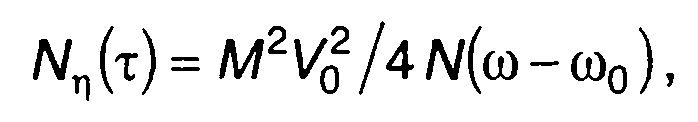(19.53)

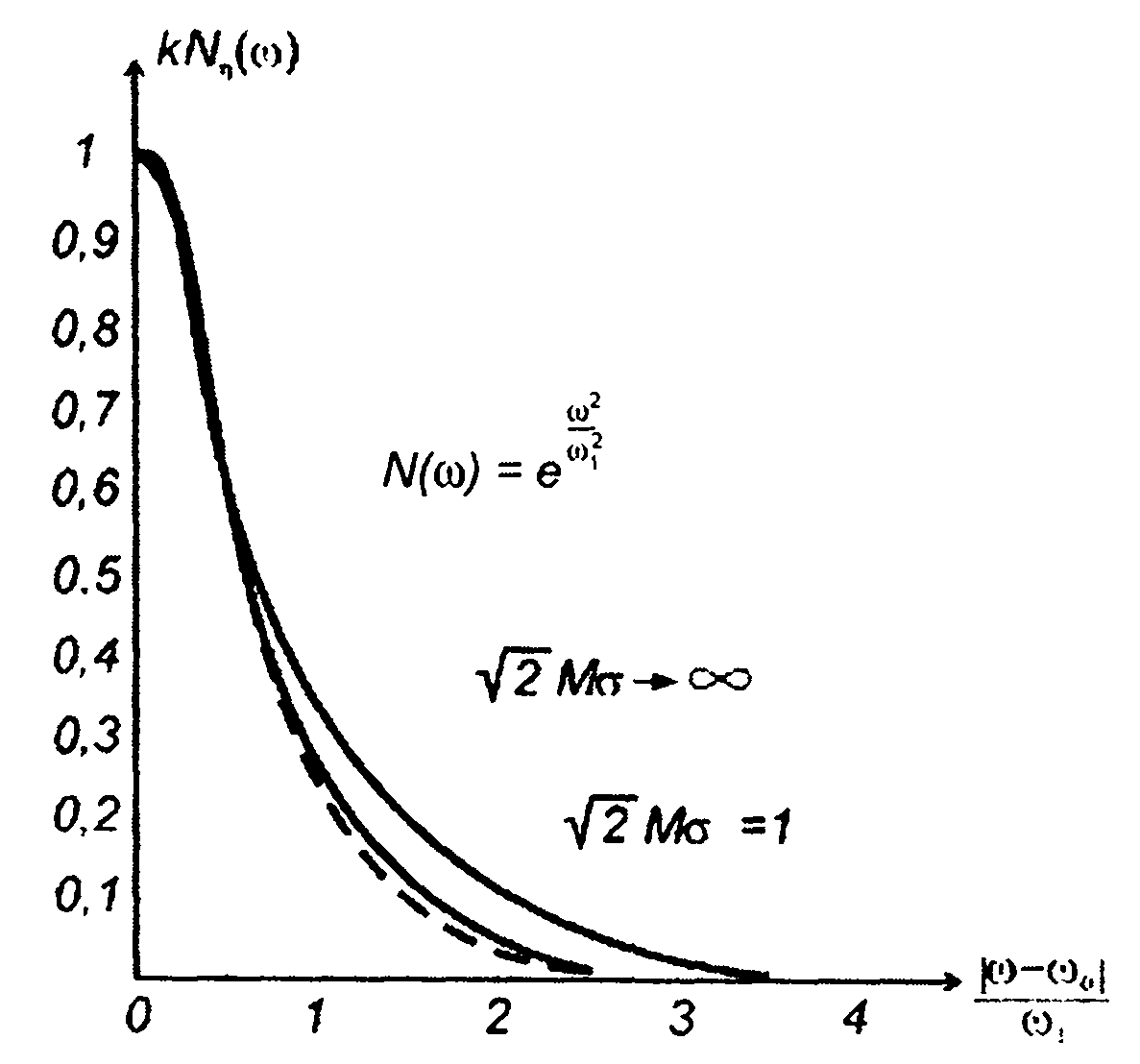
Рис. 19.18

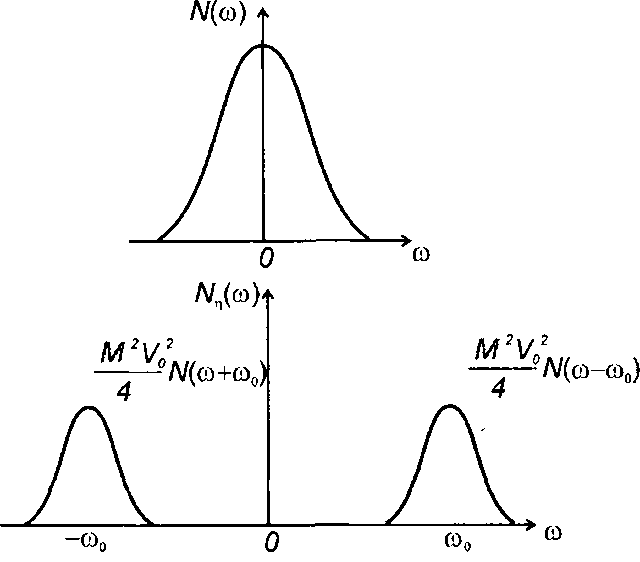
Рис. 19.19

где N(ω) - спектральная плотность мощности модулирующего слу­чайного процесса ξ(t).

Cпектр случайного процесса с балансной AM (рис. 19.19) со­держит две симметричные полосы верхних и нижних боковых со­ставляющих. Дискретная составляющая на частоте несущего коле­бания отсутствует.

19.6. Случайный процесс с угловой модуляцией

19.6.1. Описание случайного процесса с угловой модуляцией

Случайный процесс с угловой модуляцией, как правило, являет­ся узкополосным, описывается выражением (19.1), рис. 19.19,

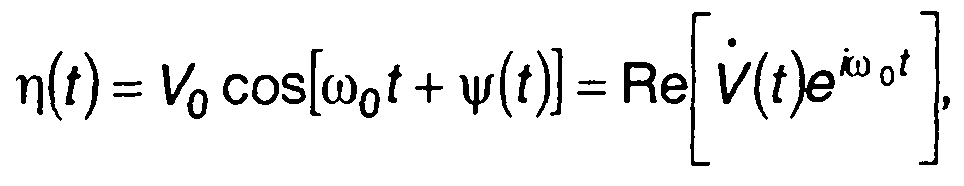(19.54)

где V₀, ω₀, Ψ(t) - амплитуда, частота и фаза; V(t) = V₀ e^^(t) - ком­плексная огибающая случайного процесса.

При угловой модуляции происходит изменение фазы несущего колебания \|i(t) под воздействием модулирующего случайного про­цесса Различают два вида угловой модуляции - фазовую (ФМ) и частотную (ЧМ).

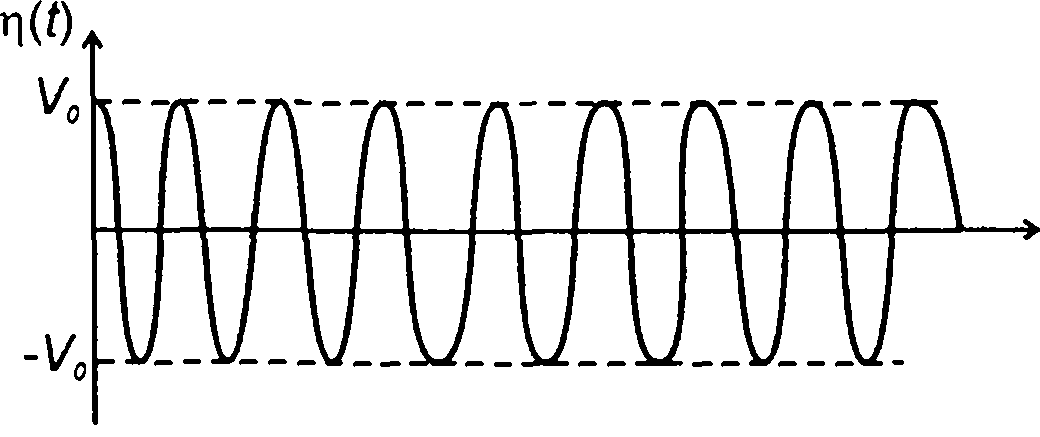
Рис. 19.19

При ФМ модулирующий случайный процесс воздействует на фазу непосредственно. Фаза определяется как

Ψ(t) = φ₀ + kξ(t), (19.55)

где φ₀ - начальная фаза; ξ(t) - модулирующее колебание - стацио­нарный центрированный случайный процесс; k - коэффициент пропорциональности.

Выражение (19.55) описывает линейную зависимость Ψ(t) от ξ(t) - это наиболее часто встречающийся случай.

Частота ФМ случайного процесса определяется выражением

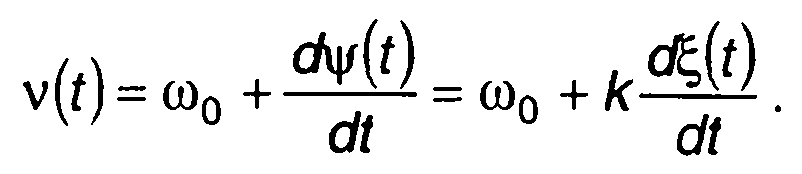(19.56)

При ЧМ модулирующее колебание воздействует непосредст­венно на частоту

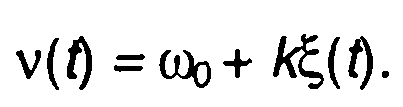(19.57)

Фаза ЧМ случайного процесса

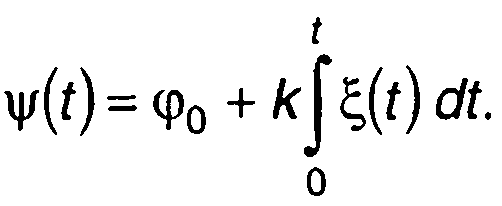(19.58)

Выражение для комплексной огибающей модулированного слу­чайного процесса записывается в виде (φ₀ =0): при ФМ

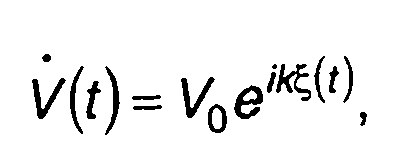(19.59)

при ЧМ

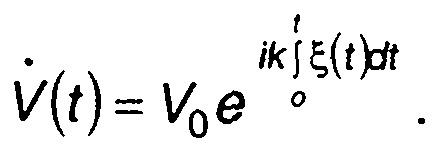(19.60)

Таким образом, если известно распределение модулирующего случайного процесса, можно найти распределение фазы и частоты модулированного случайного процесса (по крайней мере такая возможность имеется). Используя (19.59) и (19.60), получим корре­ляционную функцию и спектральную плотность мощности ком­плексной огибающей, а, следовательно, и модулированного слу­чайного процесса.

19.6.2. Распределение фазы и частоты модулированного случайного процесса

Определим ПРВ фазы и частоты модулированного случайного процесса сначала при ФМ. Обозначив f_ξ1(x) одномерную ПРВ мо­дулирующего стационарного случайного процесса ξ(t), выражение для ПРВ фазы с учетом (19.55) запишем в виде (разд. 15)

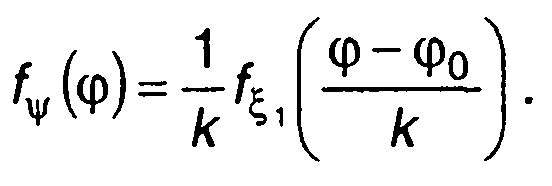(19.61)

Плотность распределения вероятностей частоты с учетом (19.56) будет равна

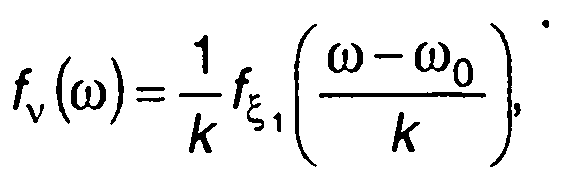(19.62)

где f_ξ1(x) - ПРВ производной модулирующего случайного процесса ξ(t) = dtξ/dt.

Для центрированного гауссовского процесса ξ(t)

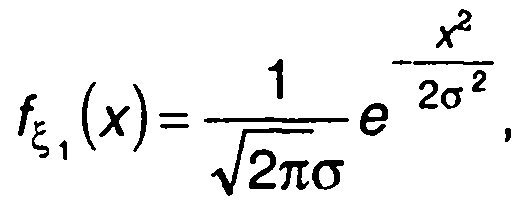(19.63)

где σ² - дисперсия ξ(t), из (19.61) получим

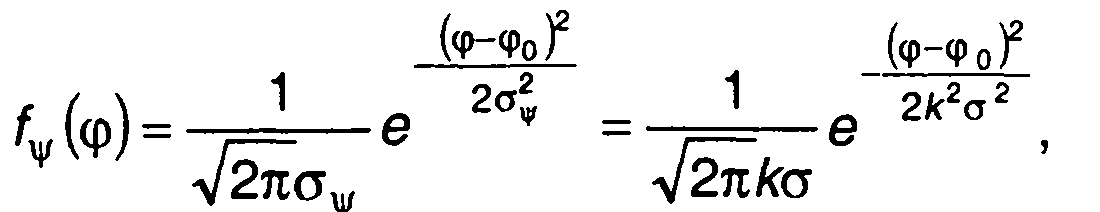(19.64)

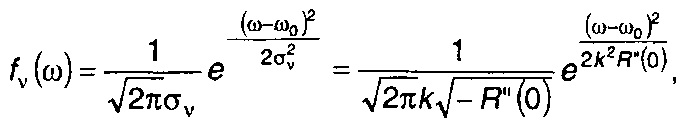(19.65)

где R(r) - корреляционная функция модулирующего процесса ξ(t);

σ_Ψ² = k²σ² , σ_v² = - k²R" (0) - дисперсии фазы и частоты.

При определении f_v(ω) учтено, что производная гауссовского процесса имеет нормальное распределение.

Плотность распределения вероятностей частоты f_v(ω) дает представление о спектре, выражение (19.65) позволяет судить о спектре ФМ случайного процесса при модуляции гауссовским про­цессом.

При ЧМ выражения для ПРВ частоты и фазы модулированного случайного процесса с учетом (19.57) и (19.58) получим в виде

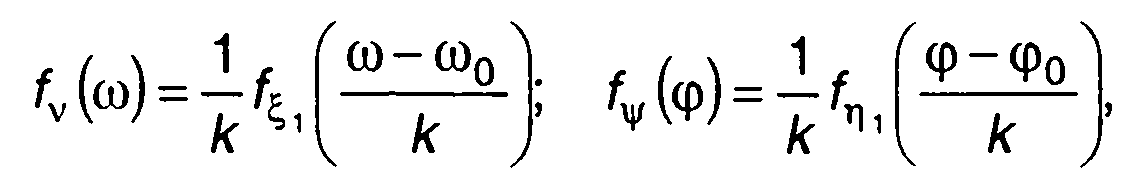(19.66)

где f_η1(y)- ПРВ интеграла от ξ(t).

Плотность распределения вероятностей частоты, описываемая (19.66), позволяет получить представление о спектре модулиро­ванного случайного процесса.

Для модулирующего гауссовского процесса ξ(t) имеем

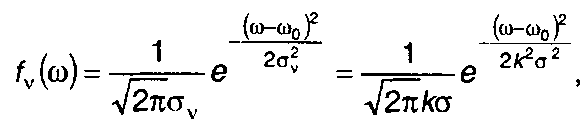(19.67)

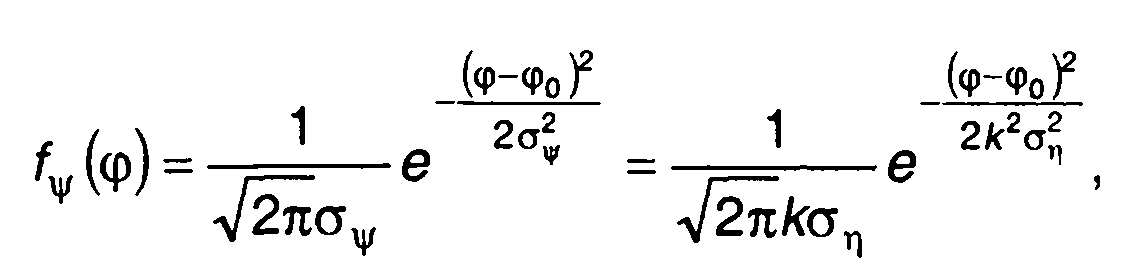(19.68)

где σ_v² = k²σ²; σ_Ψ² = k²σ_η² - дисперсия частоты и фазы; σ_η² - дис­персия интеграла от ξ(t).

Используя спектральную плотность мощности случайного про­цесса ξ(t), выражения для σ_v² и σ_Ψ² запишем в виде

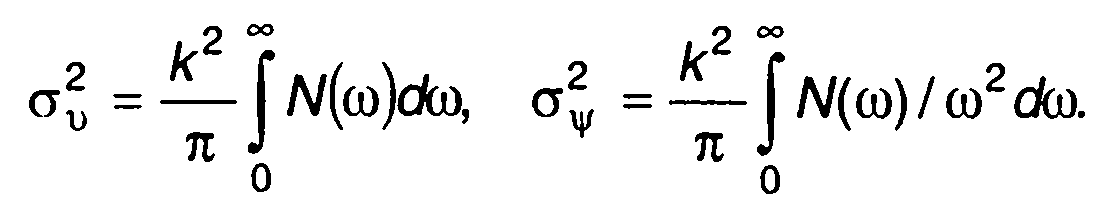
Сравнение характеристик распределения фазы и частоты при ФМ и ЧМ показывает, что отличие ФМ от ЧМ при модуляции слу­чайными процессами такое же, как при модуляции детерминиро­ванными сигналами.

При описании угловой модуляции детерминированными сигна­лами пользуются такими характеристиками, как индекс модуляции

и девиация частоты. При рассмотрении угловой модуляции слу­чайных процессов их определения требуют уточнения.

При ФМ случайным процессом целесообразно рассматривать эффективный индекс модуляции, определив его как

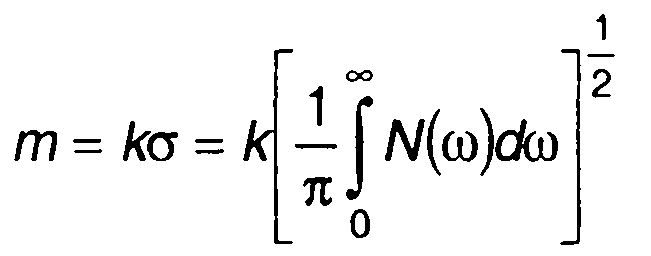(19.69)

и эффективную девиацию частоты

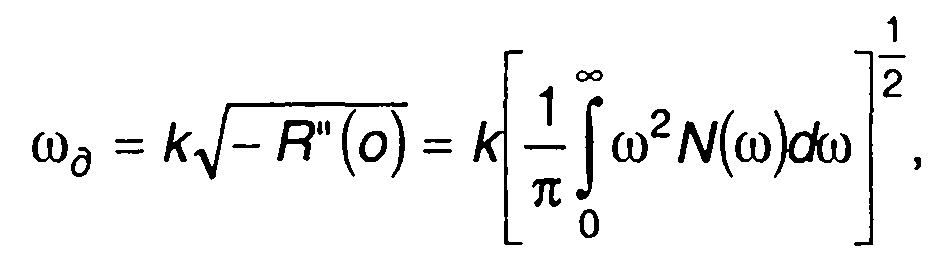(19.70)

где R(t), σ² = R(0) - корреляционная функция и дисперсия модули­рующего случайного процесса ξ(t).

При ЧМ эффективную девиацию частоты определим как

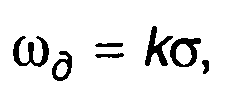(19.71)

а эффективный индекс модуляции

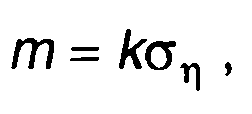(19.72)

где

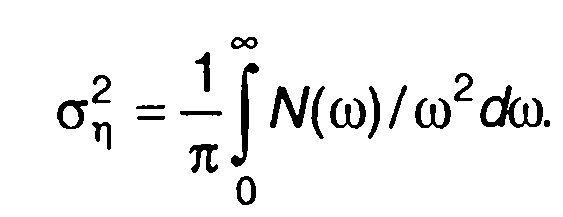
Здесь N(ω) - спектральная плотность мощности случайного про­цесса ξ(t).

При модуляции случайным процессом пределы изменения час­тоты не ограничены. В то же время при соответствующем соотно­шении эффективной девиации и несущей частоты вероятностью того, что случайная величина - частота примет отрицательные значения, можно пренебречь. Это условие и означает узкополосность модулированного случайного процесса. В рамках этого усло­вия и проводится рассмотрение модулированных случайных про­цессов.

19.6.3. Корреляционная функция и спектральная плотность мощности комплексной огибающей ФМ случайного процесса

Корреляционная функция комплексной огибающей модулиро­ванного случайного процесса определяется выражением (19.9)

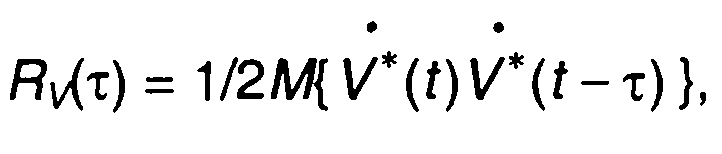
где М[...} - символ усреднения.

При ФМ с учетом (19.55) запишем

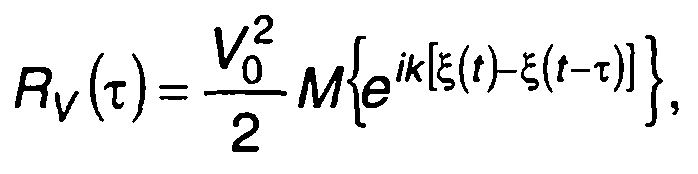(19.73)

где ξ(t) - модулирующий случайный процесс.

Среднее значение в (19.73) представляет характеристическую функцию случайного процесса (разд. 15)

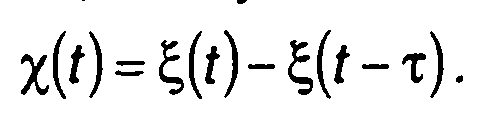(19.74)

Она определяется выражением

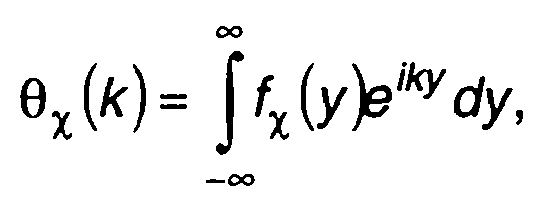
где f_x (у) - одномерная ПРВ случайного процесса X(t).

Плотность распределения вероятности X(t) получим с учетом (19.74), зная ПРВ модулирующего случайного процесса ξ(t) (разд. 15)

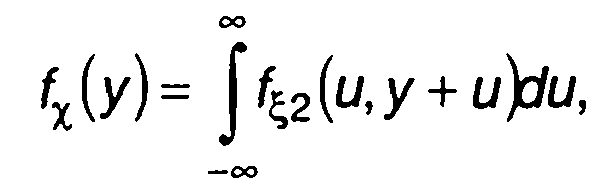(19.75)

где f_ξ2(x₁,х₂) - двумерная ПРВ случайного процесса ξ(t).

При модуляции гауссовским процессом распределение X(t) яв­ляется нормальным. Характеристическая функция X(t) равна

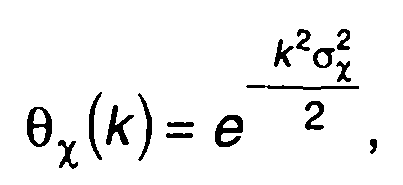(19.76)

где σ_х² - дисперсия X(t)-

При нормальном распределении ξ(t) получим

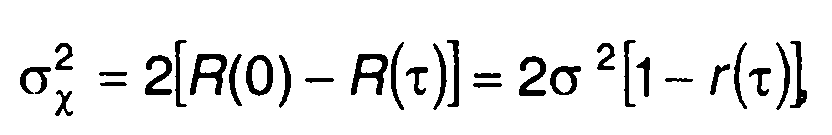(19.77)

где R('τ), σ² = R(0), r(τ) = R(τ)/R(0) - корреляционная функция, дис­персия и нормированная корреляционная функция модулирующего случайного процесса ξ(t).

При модуляции гауссовским процессом из (19.73) с учетом (19.76) и (19.77) получим

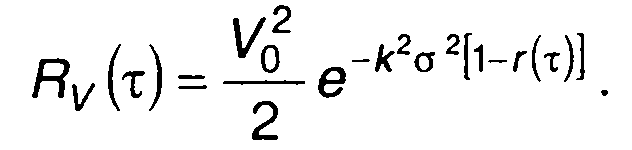(19.78)

Используя спектральную плотность мощности модулирующего случайного процесса N(ω), выражение для R_v(τ) представим в виде

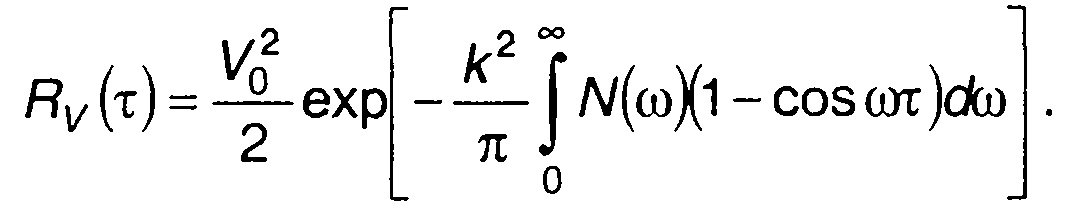(19.79)

Полученные выражения описывают зависимость корреляцион­ной функций комплексной огибающей ФМ сигнала от спектра мо­дулирующего случайного процесса.

Корреляционная функция ФМ случайного процесса определяет­ся (19.8). С учетом (19.79) запишем

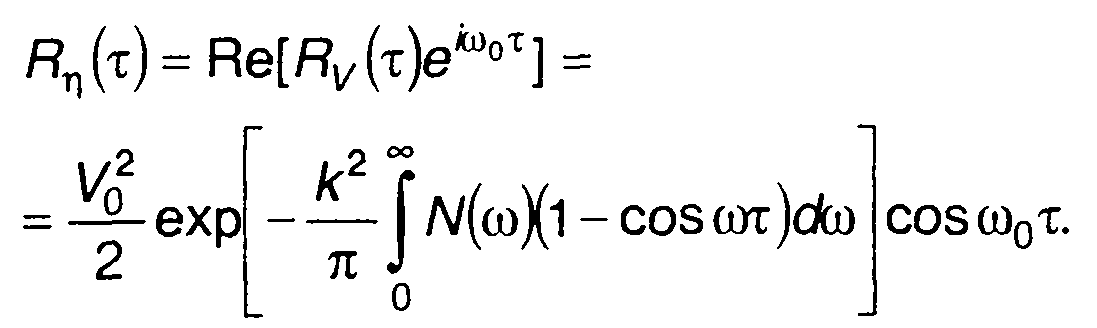(19.80)

В качестве примеров рассмотрим некоторые виды модулирую­щих случайных процессов.

1. Спектр модулирующего случайного процесса - равномерный в полосе частот (табл. 18.1, п.1), рис. 19.20.

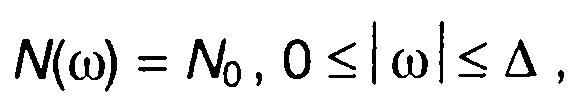
корреляционная функция

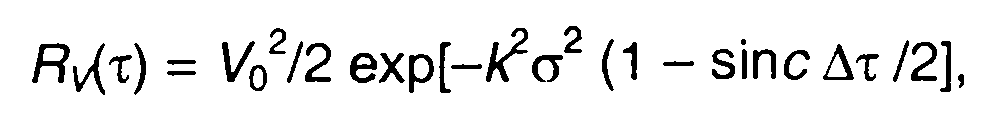
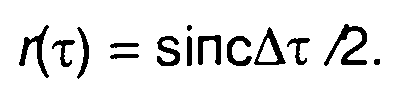
Корреляционная функция комплексной огибающей равна

где σ² - дисперсия модулирующего случайного процесса.

График корреляционной функции комплексной огибающей при­веден на том же рис. 19.20,а.

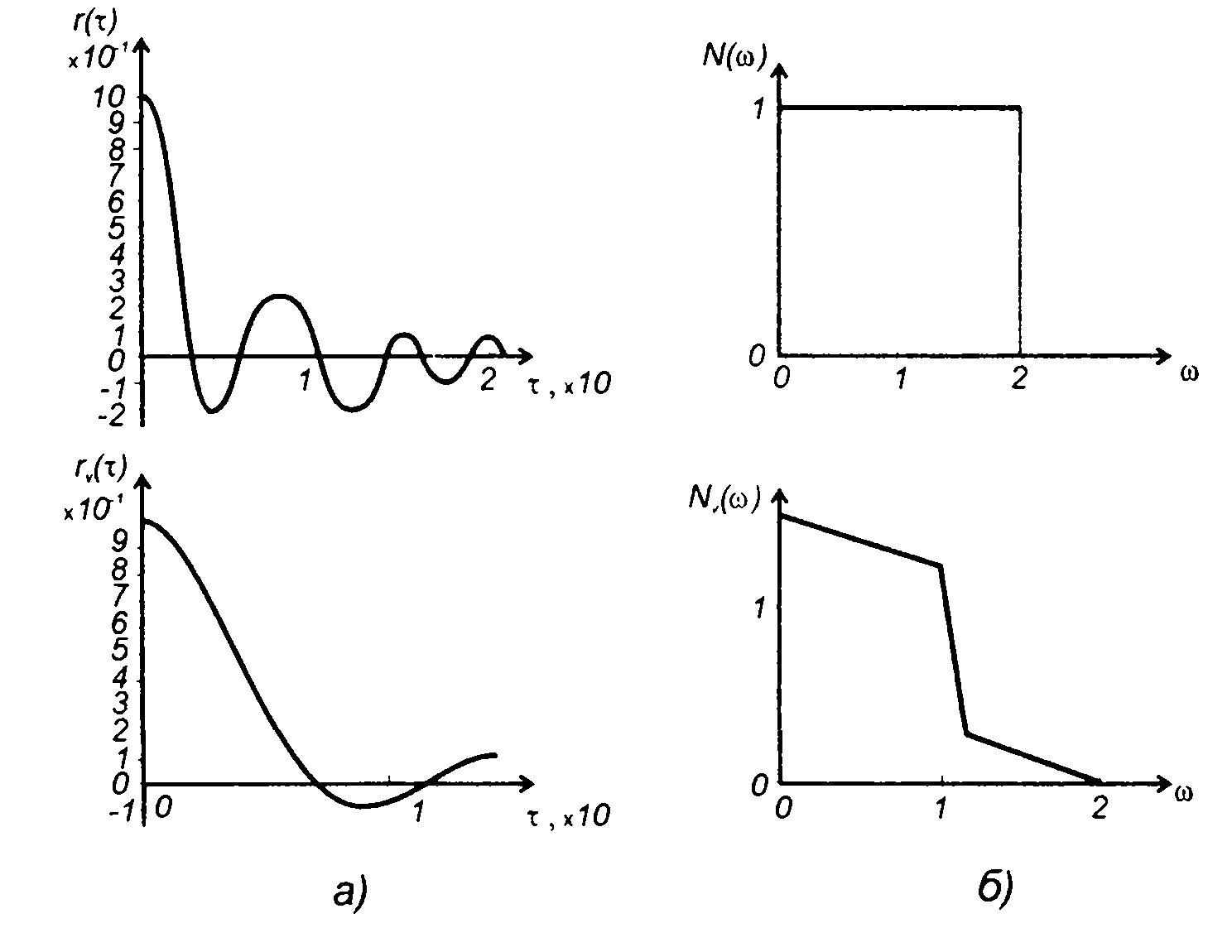
Рис. 19.20

2. Спектр модулирующего случайного процесса вида (табл. 18.1, п.З), рис. 19.21.

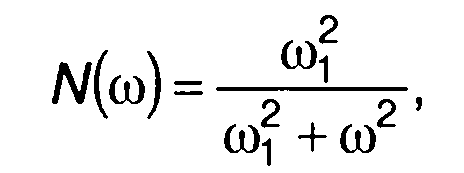
нормированная корреляционная функция

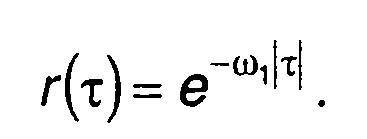
Корреляционная функция комплексной огибающей

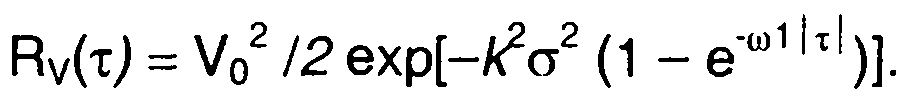
График корреляционной функции комплексной огибающей при­веден на рис. 19.21,а.

3. Спектр модулирующего случайного процесса - гауссовского вида (табл. 18.1, п. 13), рис. 19.22.

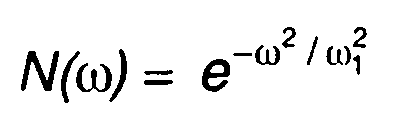
нормированная корреляционная функция

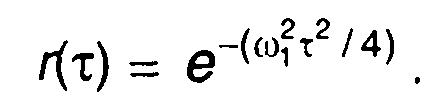
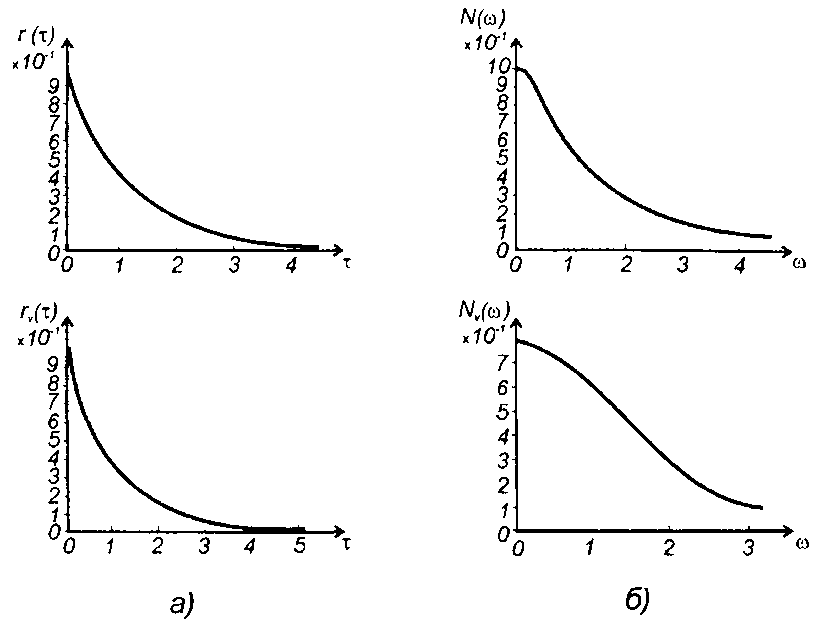
Рис. 19.21

Корреляционная функция комплексной огибающей равна

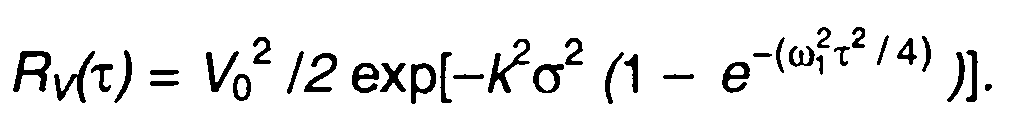
График корреляционной функции комплексной огибающей при­веден на рис. 19.22, а.

Средняя мощность модулированного случайного процесса рав­на Rη(0)

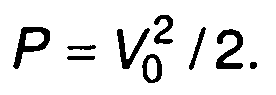(19.81)

При τ→∞ имеем

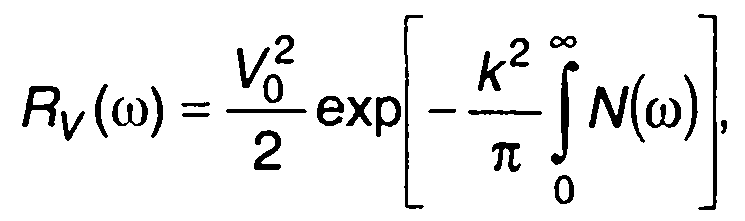(19.82)

Непрерывной части спектра соответствует

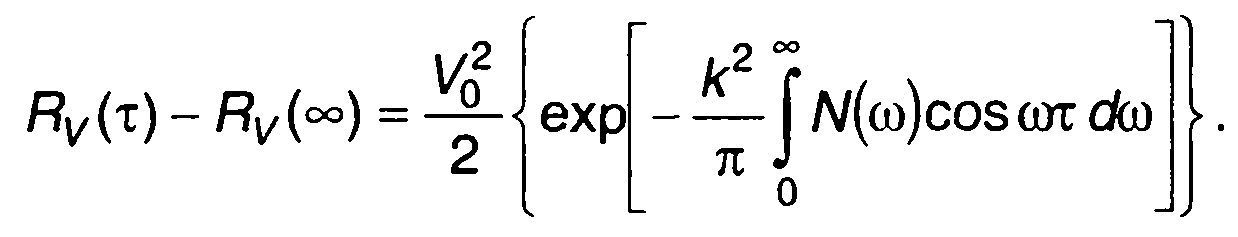(19.83)

Спектральная плотность мощности комплексной огибающей ФМ

случайного процесса определяется как

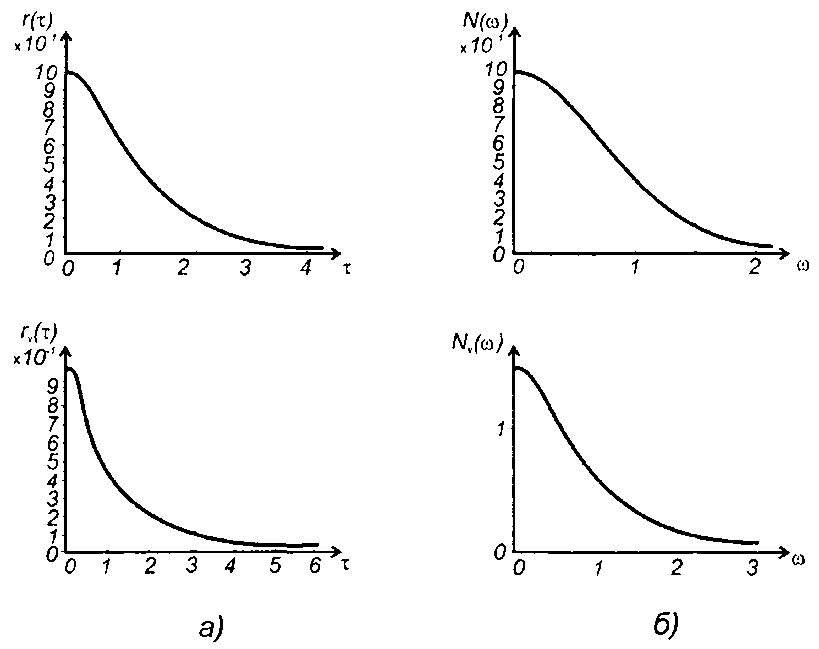
Рис. 19.22

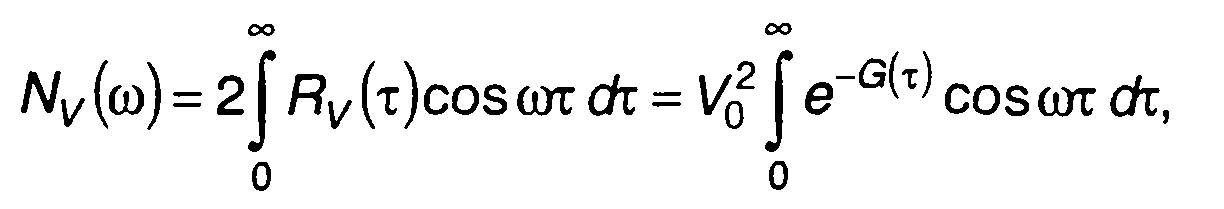(19.84)

где

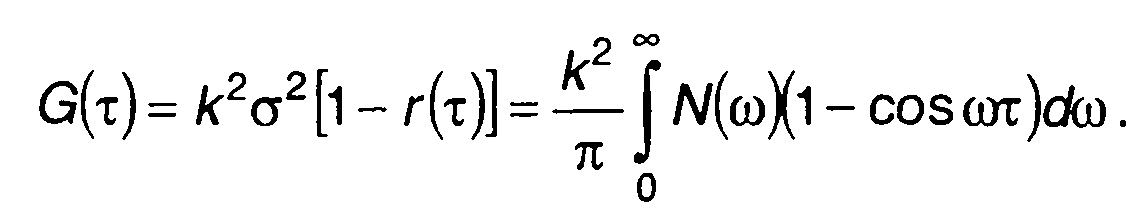(19.85)