ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 22 страница

В качестве примеров рассмотрим некоторые виды модулирую­щих случайных процессов.

1. Спектр и корреляционная функция модулирующего процесса, описываемого в табл. 18.1, п. 1.

Спектральная плотность комплексной огибающей модулирован­ного случайного процесса (рис. 19.20,6)

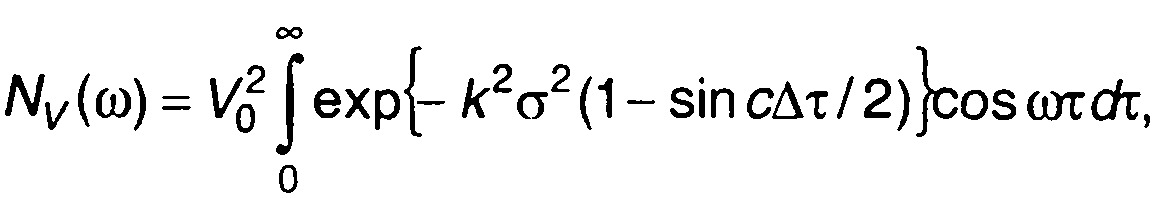
где σ²-дисперсия модулирующего случайного процесса.

2. Спектр и корреляционная функция модулирующего процесса, описываемого в табл. 18.1, п.З.

Спектральная плотность комплексной огибающей модулирован­ного случайного процесса (рис. 19.21 ,б)

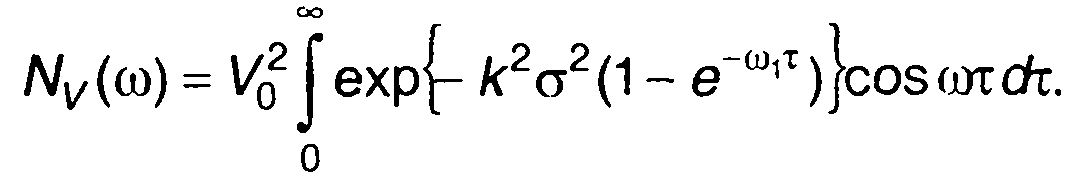
3. Спектр и корреляционная функция модулирующего случайно­го процесса, описываемого в табл. 18.1, п. 13.

Спектральная плотность комплексной огибающей модулирован­ного случайного процесса (рис. 19.22,б).

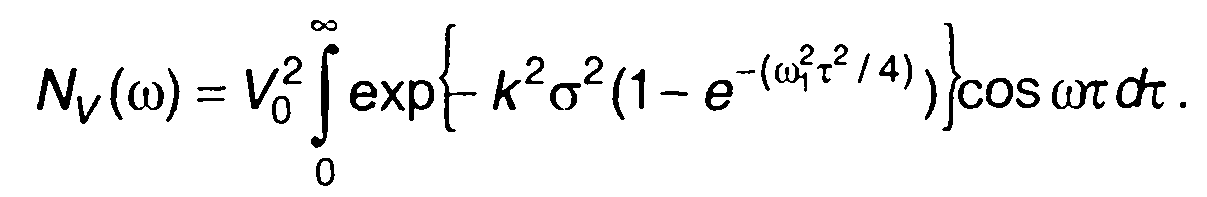
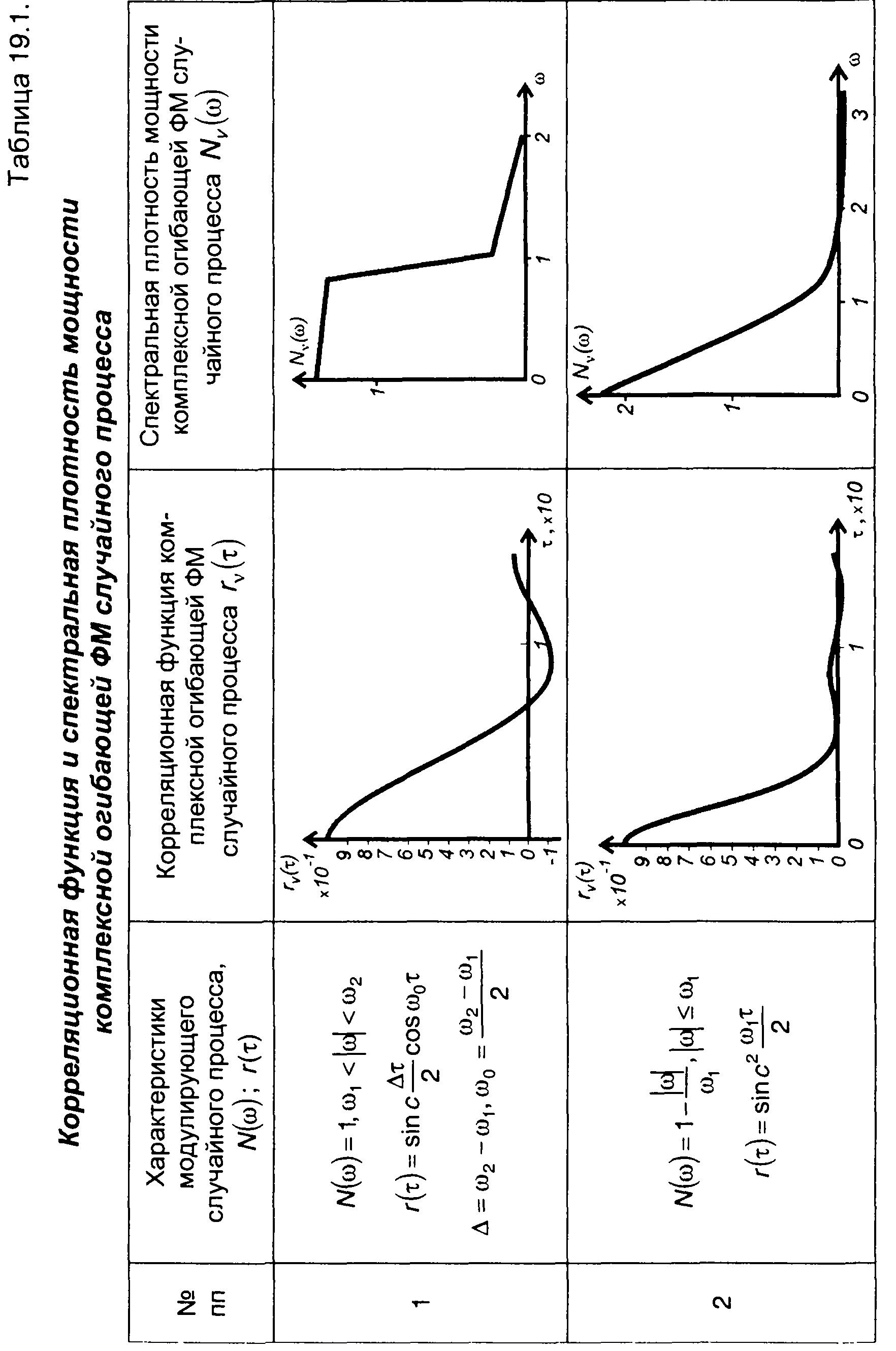
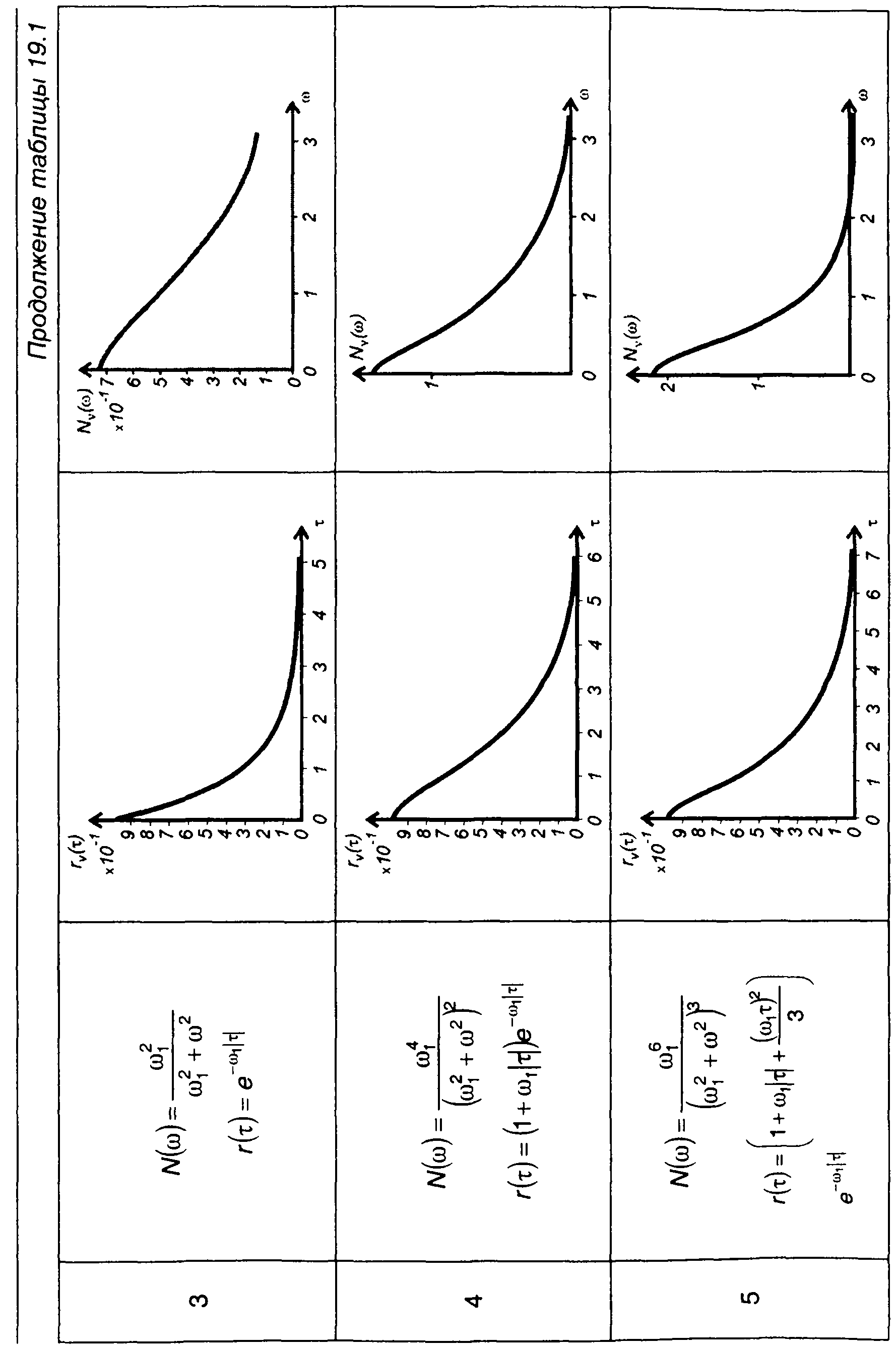
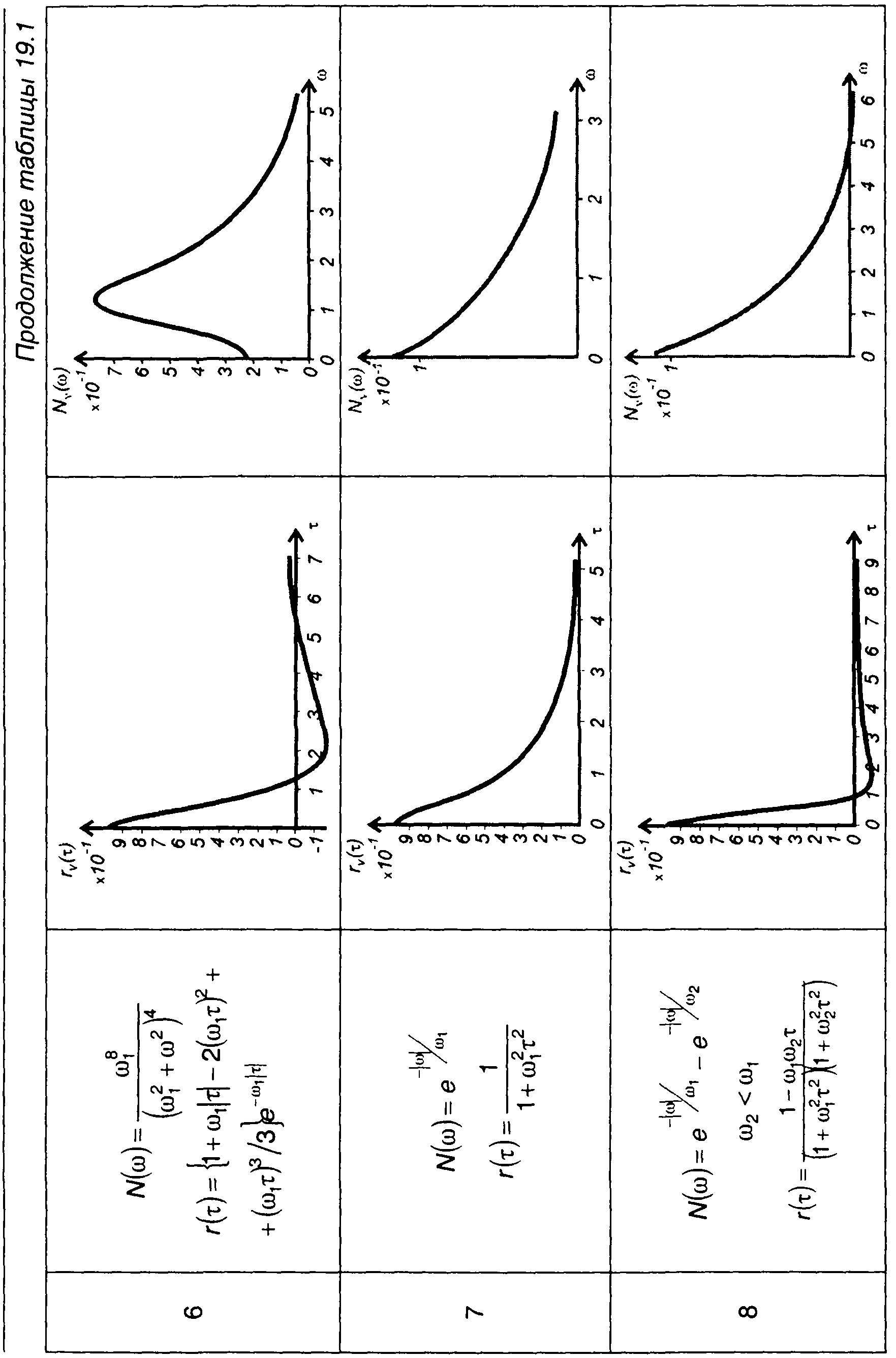
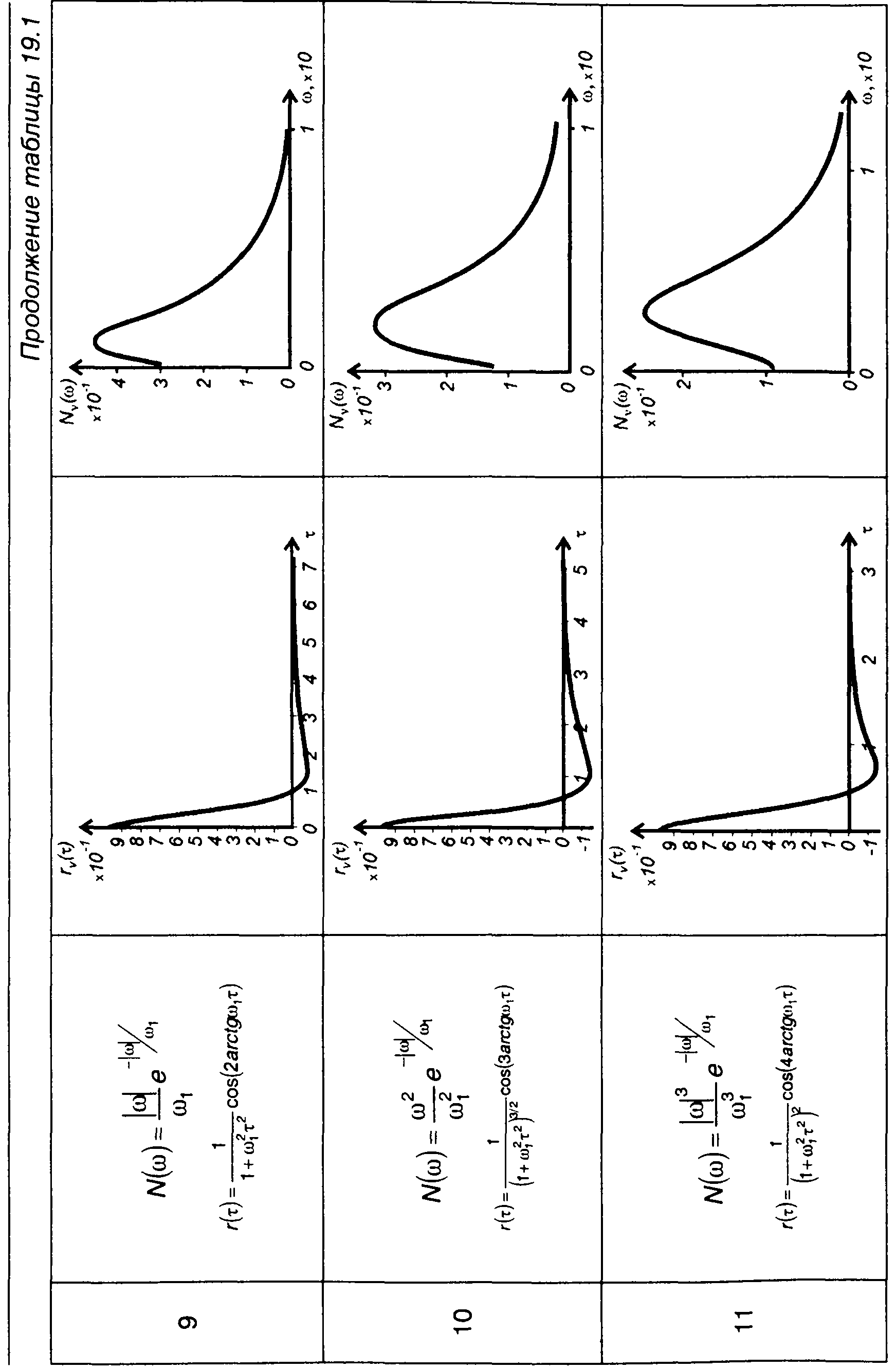
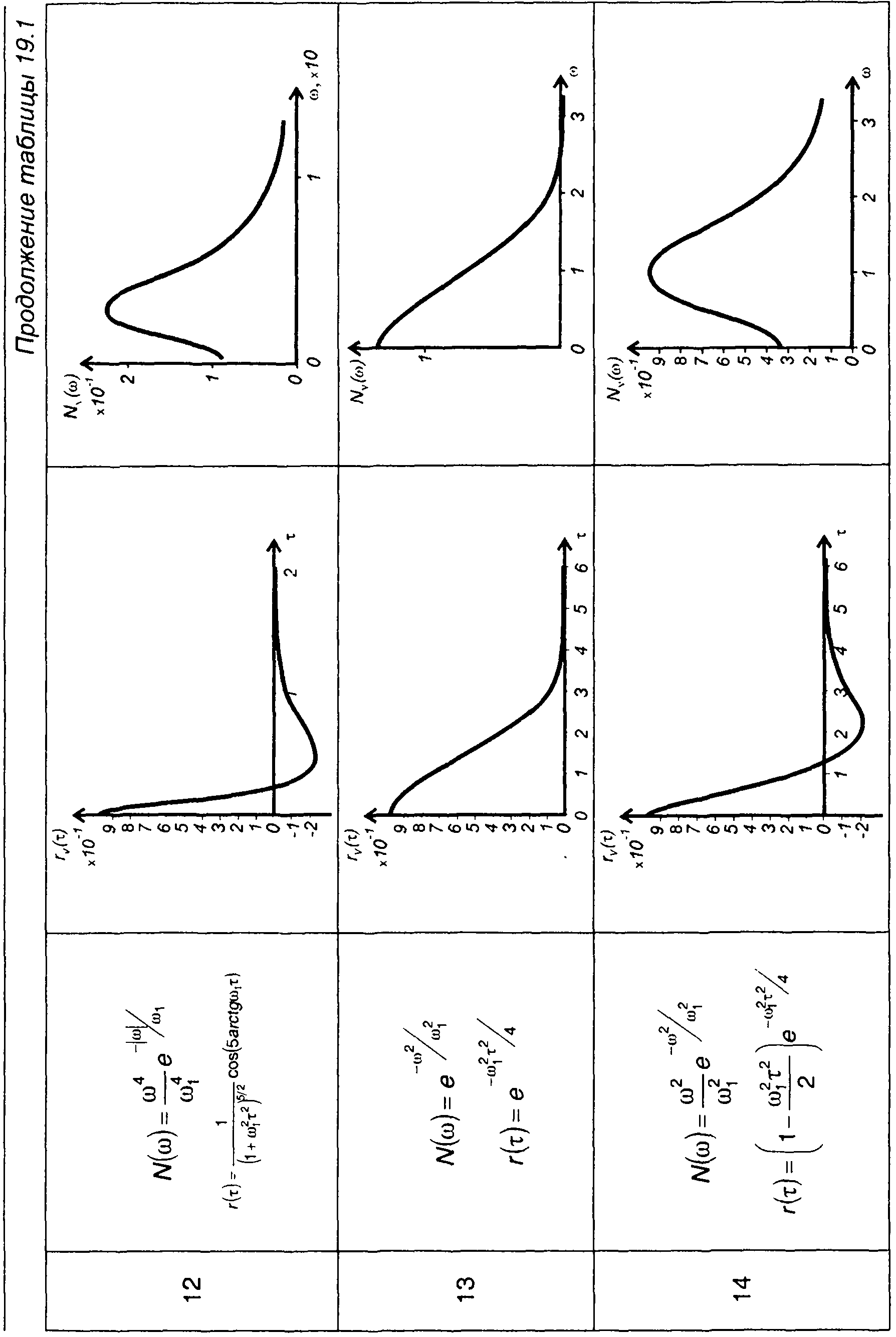
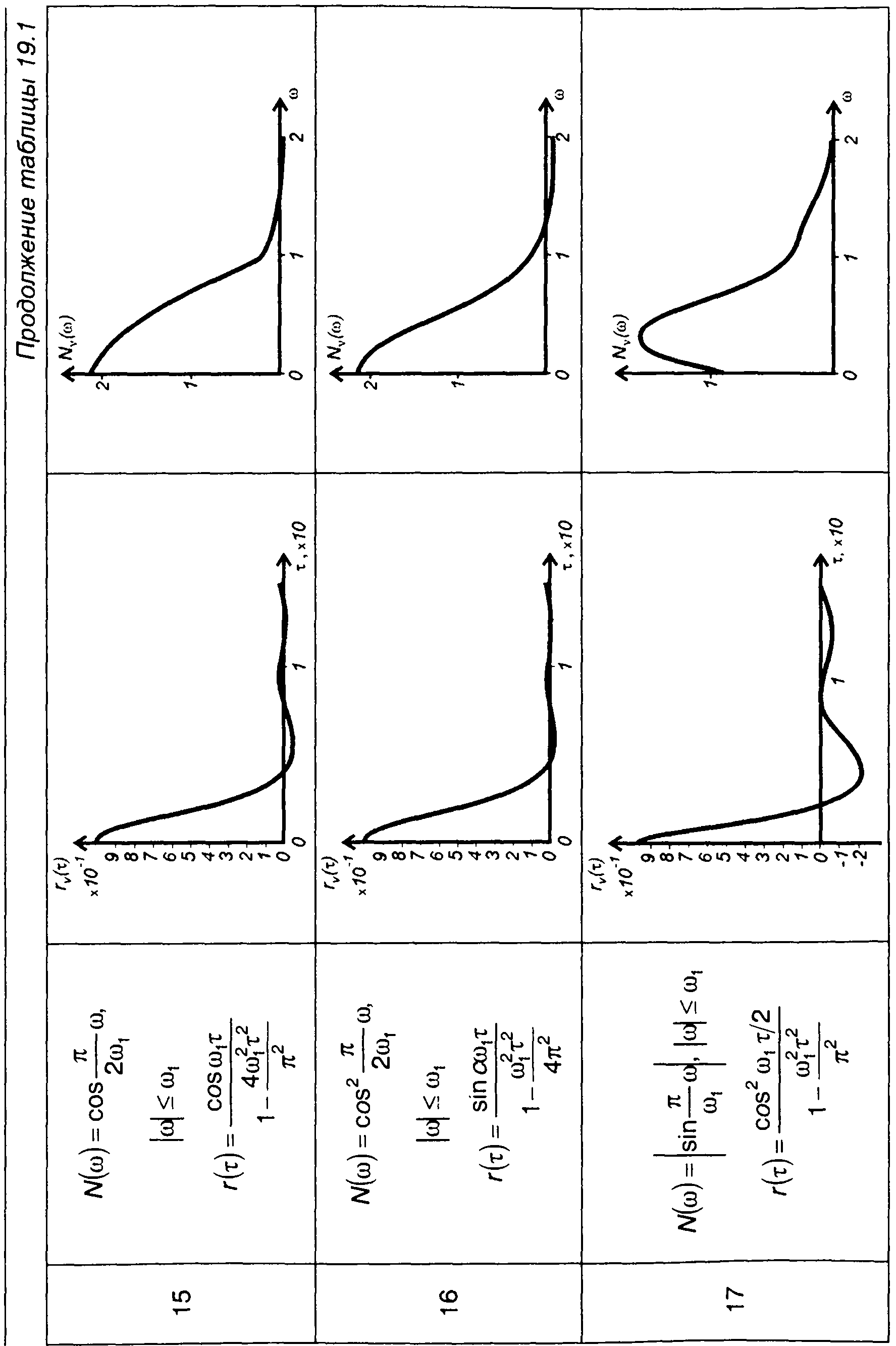
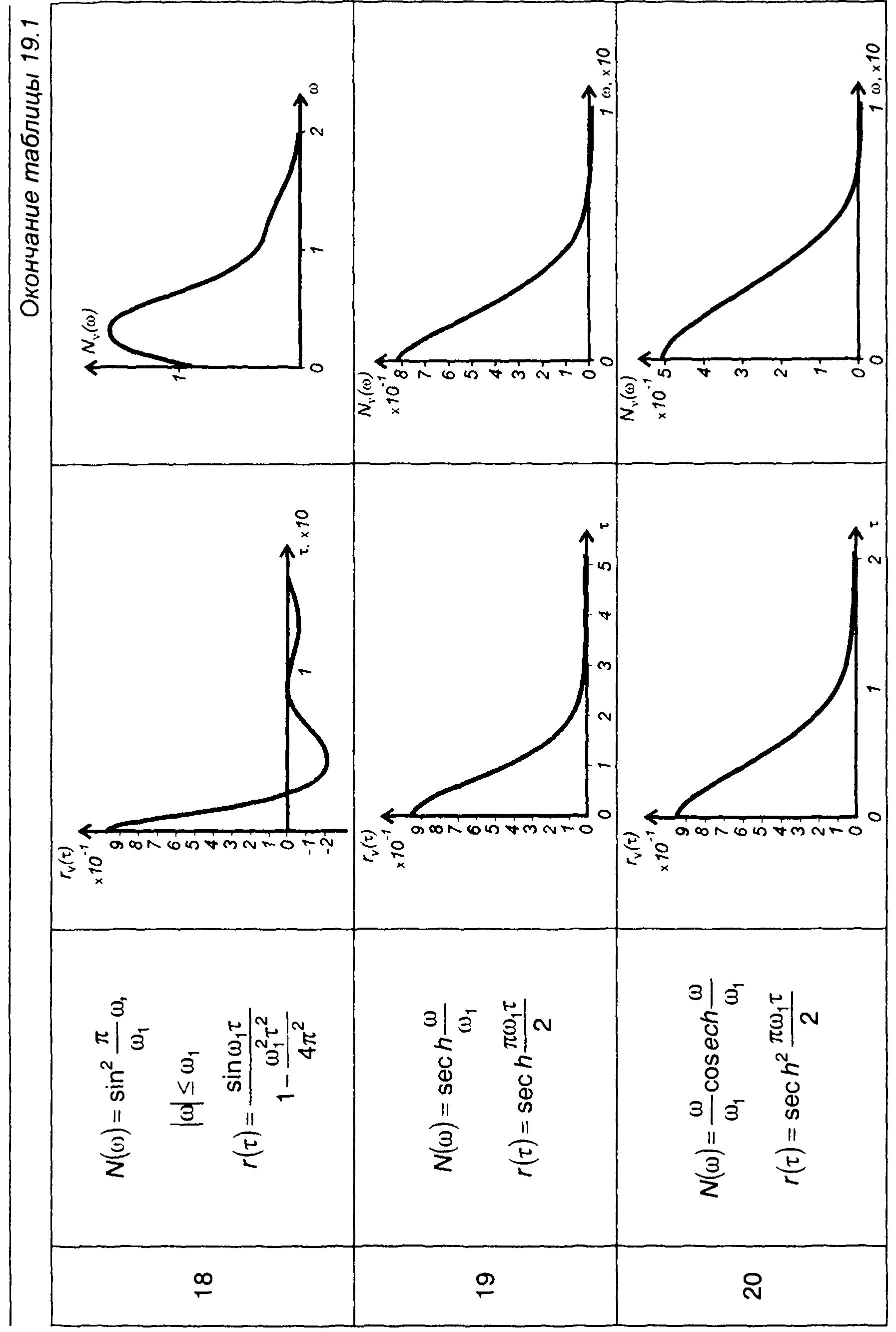
Графики корреляционных функций и спектров комплексной оги­бающей ФМ случайных процессов, модулированных случайными процессами, характеристики которых приведены в табл. 18.1, даны в табл. 19.1.

Переход от спектральной плотности мощности комплексной огибающей к спектральной плотности мощности узкополосного случайного процесса описывается (19.11)

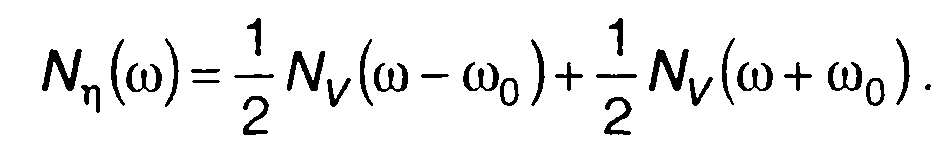(19.86)

В (19.84), раскладывая r(τ) в ряд Тейлора и ограничиваясь первыми двумя слагаемыми, получим

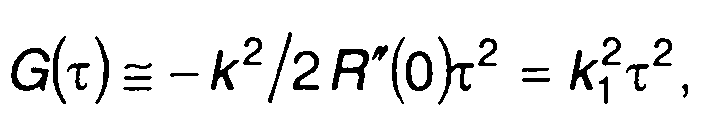(19.87)

где k = k₁k√(- R"(0)/2).

Подставляя (19.87) в (19.84), запишем

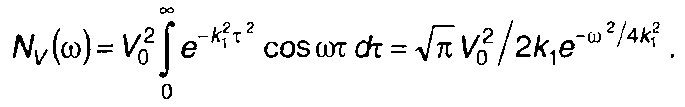(19.88)

Спектральная плотность мощности модулированного случайно­го процесса описывается выражением (19.11). С учетом (19.88) для нее получим при ω > 0

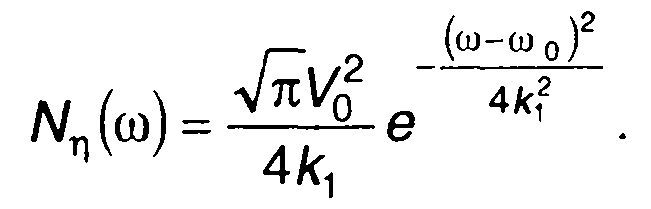(19.89)

Как следует из полученных выражений, при принятой аппрокси­мации корреляционной функции модулирующего случайного про­цесса спектральная плотность мощности описывается гауссовской функцией.

При малом индексе модуляции, kσ << 1, в (19.78) может принять

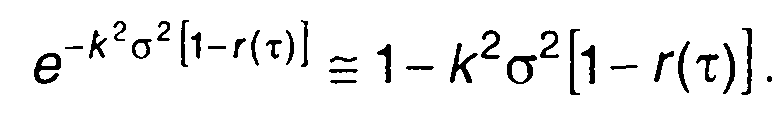(19.90)

Спектральная плотность мощности комплексной огибающей по­лучается с учетом (1.83) и (19.90) в виде

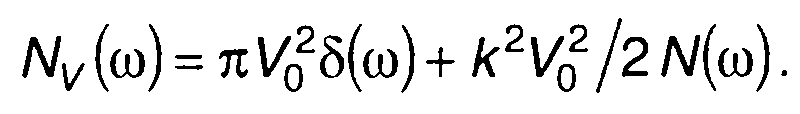(19.91)

Как следует из (19.91), при малом индексе модуляции непре­рывная часть спектра повторяет (по форме) спектр модулирующего случайного процесса.

19.6.4. Корреляционная функция и спектральная плотность мощности комплексной огибающей ЧМ случайного процесса

Частотно-модулированный случайный процесс описывается вы­ражением

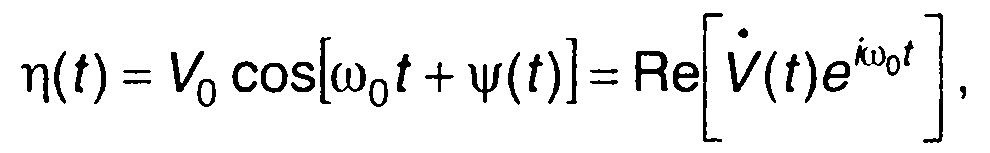
где V(t) = V₀(t)e^iΨ(t) - комплексная огибающая.

Корреляционная функция комплексной огибающей ЧМ случай­ного процесса определяется (19.9); с учетом (19.58) выражение для нее имеет вид

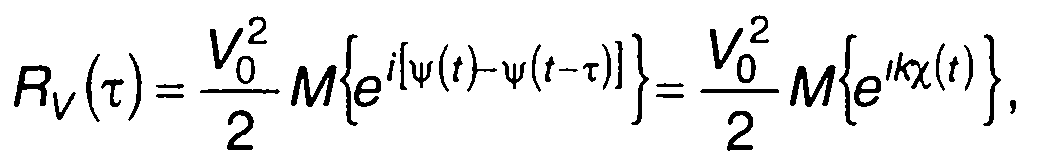(19.92)

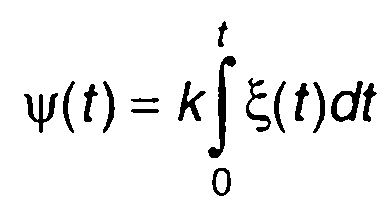- фаза случайного процесса;

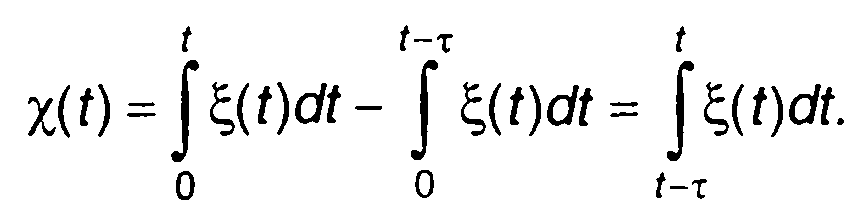
Усредненная величина в (19.92) представляет характеристиче­скую функцию X(t). Она определяется как

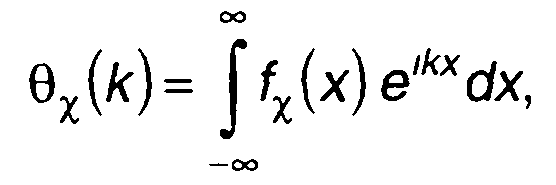(19.93)

где f_x(x) - одномерная ПРВ случайной величины X(t).

При нормальном распределении модулирующего случайного процесса ξ(t) случайные процессы

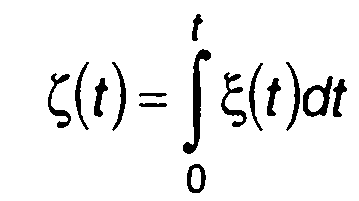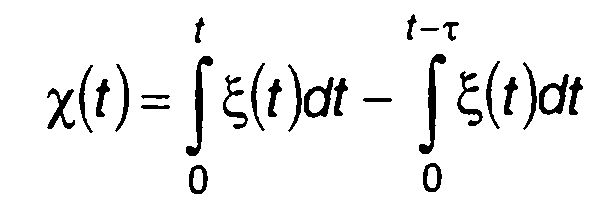и (19.94)

имеют также нормальное распределение. С учетом определения характеристической функции гауссовского процесса выражение для R_v(τ) по аналогии с (19.75) получим в виде

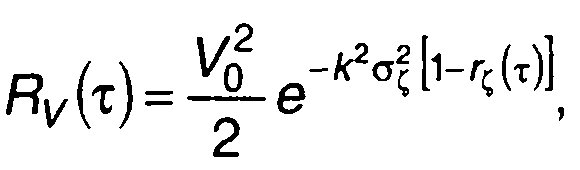(19.95)

где 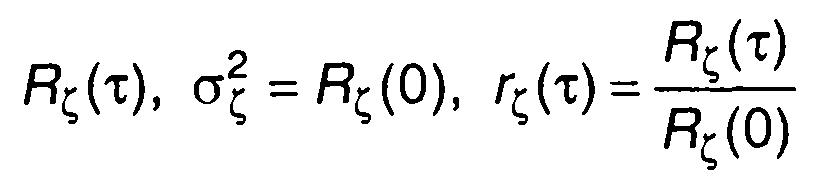- корреляционная функция,

дисперсия и нормированная корреляционная функция случайного процесса ξ(t).

Определяя корреляционную функцию ξ(t) через спектральную плотность мощности модулирующего процесса N(ω), запишем

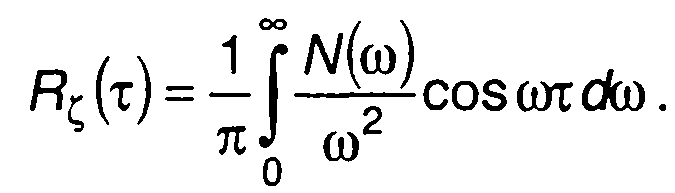(19.96)

С учетом (19.96) выражение для R_v(т) представим в виде

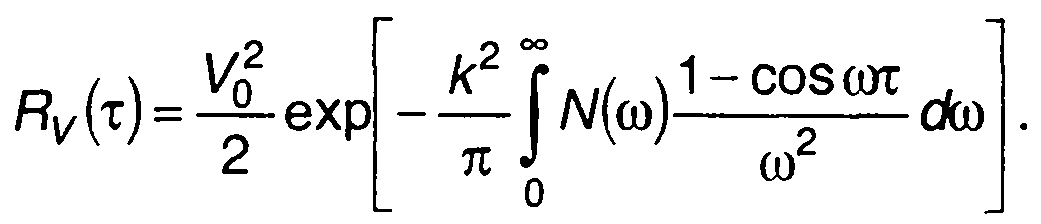(19.97)

Спектральная плотность мощности комплексной огибающей ЧМ случайного процесса описывается выражением

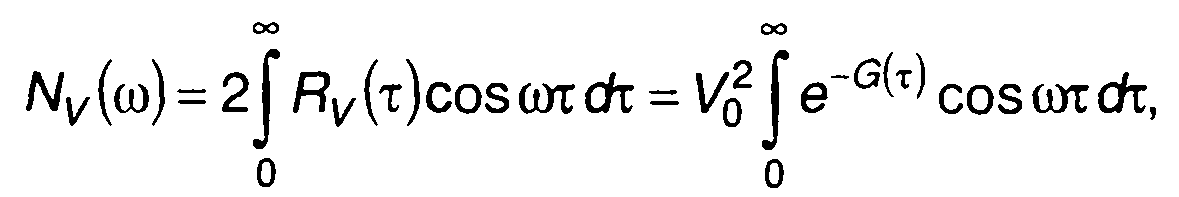(19.98)

где

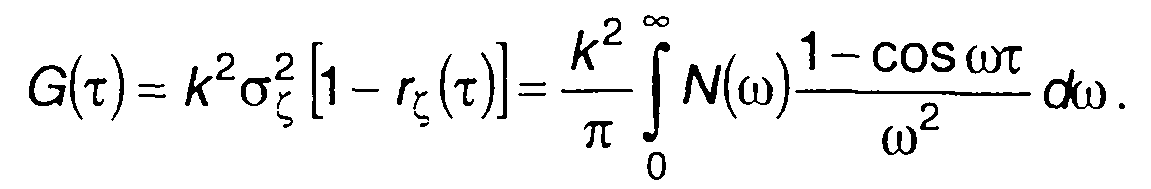(19.99)

Выражение (19.98) аналогично выражению, описывающему спектральную плотность мощности комплексной огибающей ФМ случайного процесса. Отличие заключается в определении G(τ).

ЧМ случайный процесс можно представить как ФМ случайный про­цесс, имеющий иную спектральную плотность мощности. Если спектральная плотность мощности модулирующего случайного процесса при ФМ N(ω), то при соответствующей ЧМ - N(ω)/ω².

Корреляционная функция ЧМ случайного процесса определяет­ся как

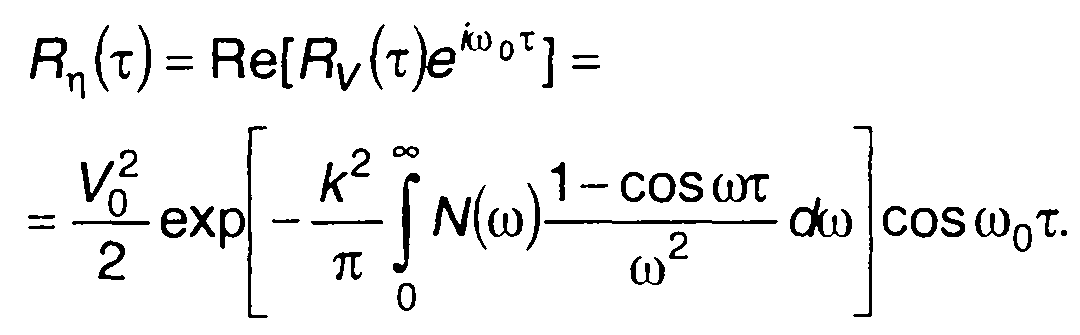(19.100)

Средняя мощность модулированного случайного процесса равна

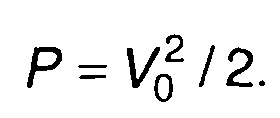(19.101)

При т→∞имеем

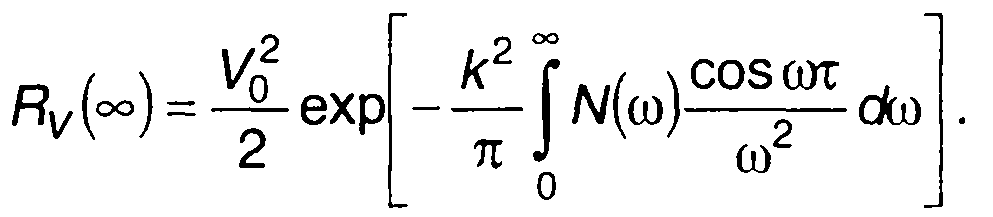(19.102)

Непрерывной части спектра соответствует

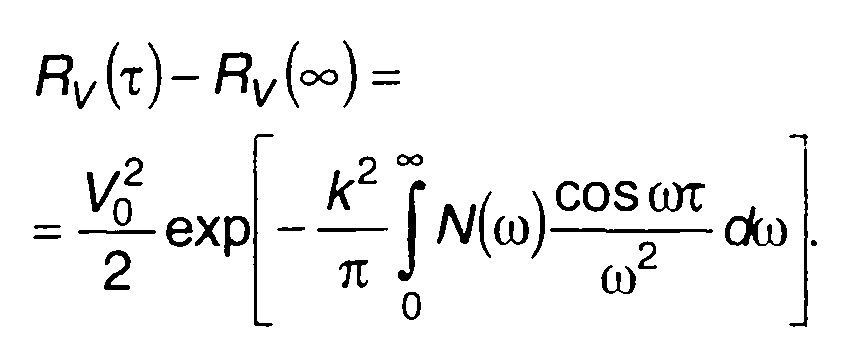(19.103)

В качестве примеров рассмотрим некоторые виды модулирую­щих случайных процессов.

1. Спектральная плотность мощности и корреляционная функция модулирующего случайного процесса описаны в табл. 18.1, п. 10.

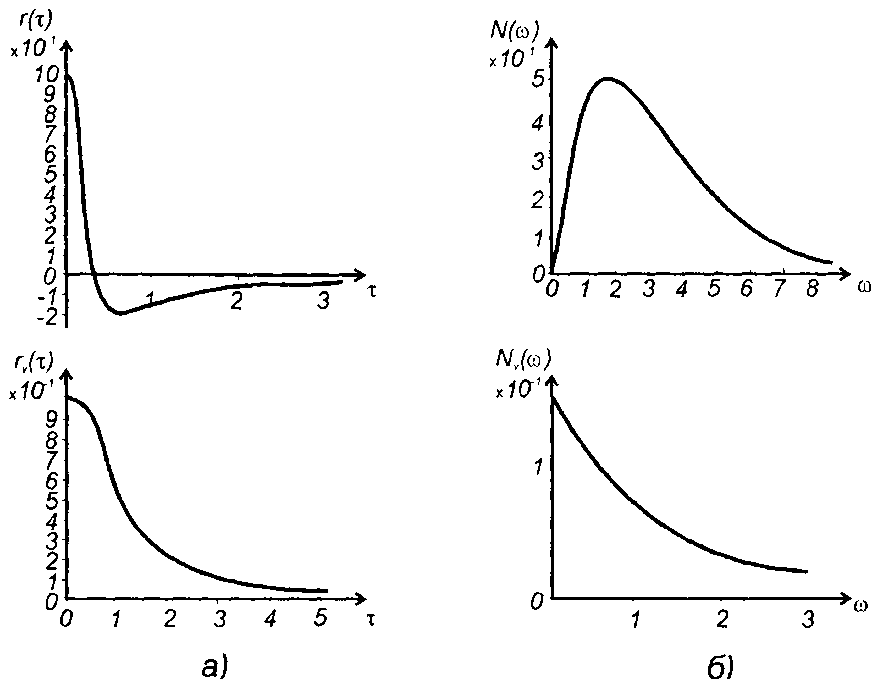
Рис. 19.23

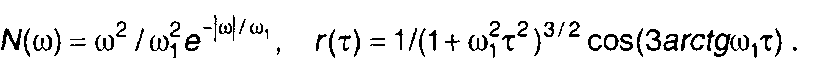
Корреляционная функция комплексной огибающей модулиро­ванного случайного процесса (рис. 19.23,а)

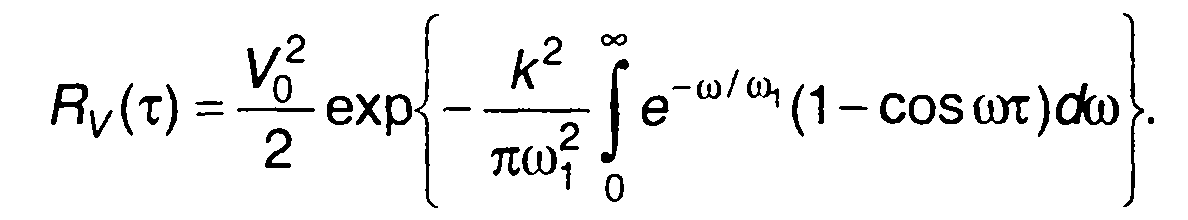
График спектральной плотности мощности огибающей модули­рованного случайного процесса (19.98) изображен на рис. 19.23,б.

2. Спектральная плотность мощности и корреляционная функ­ция модулирующего процесса описаны в табл. 18.1, п. 11.

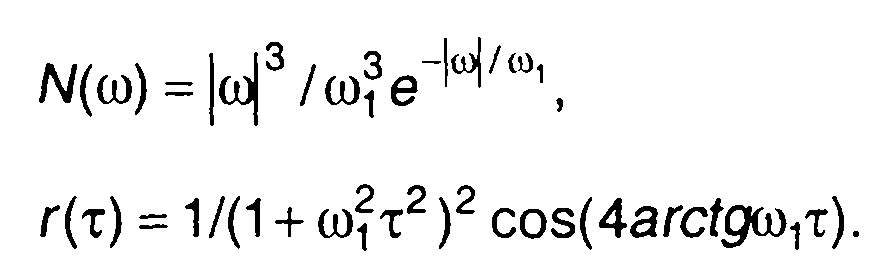
Корреляционная функция комплексной огибающей модулиро­ванного случайного процесса (рис. 19.24,а)

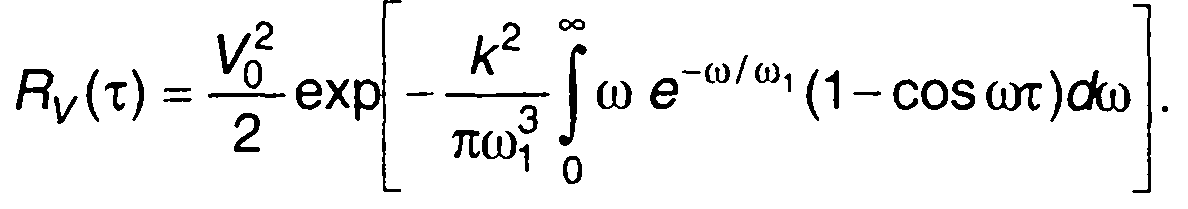
График спектральной плотности мощности комплексной оги­бающей модулированного случайного процесса (19.98) изображен на рис. 19.24,б.

3. Спектральная плотность мощности и корреляционная функция модулирующего случайного процесса описаны в табл. 18.1, п. 12.

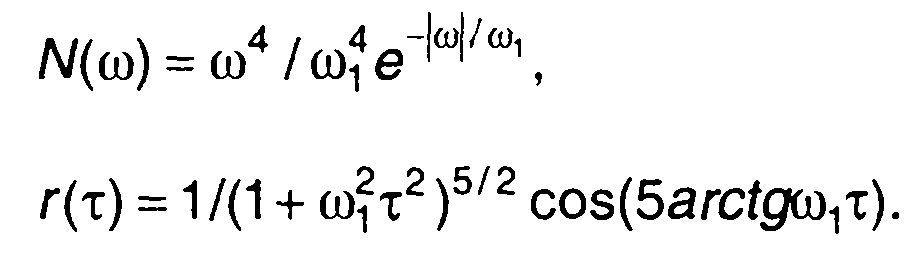
Корреляционная функция комплексной огибающей модулиро­ванного случайного процесса (рис. 19.25,а)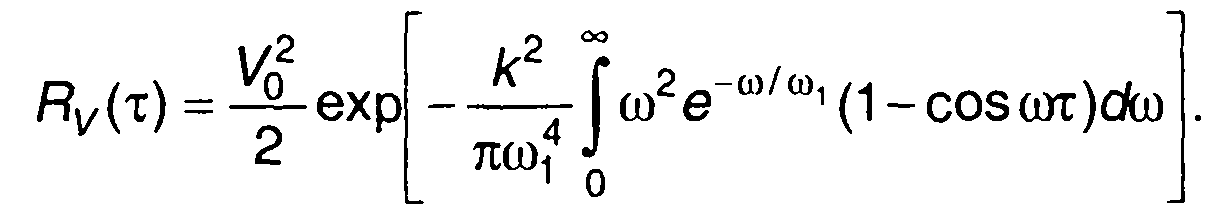

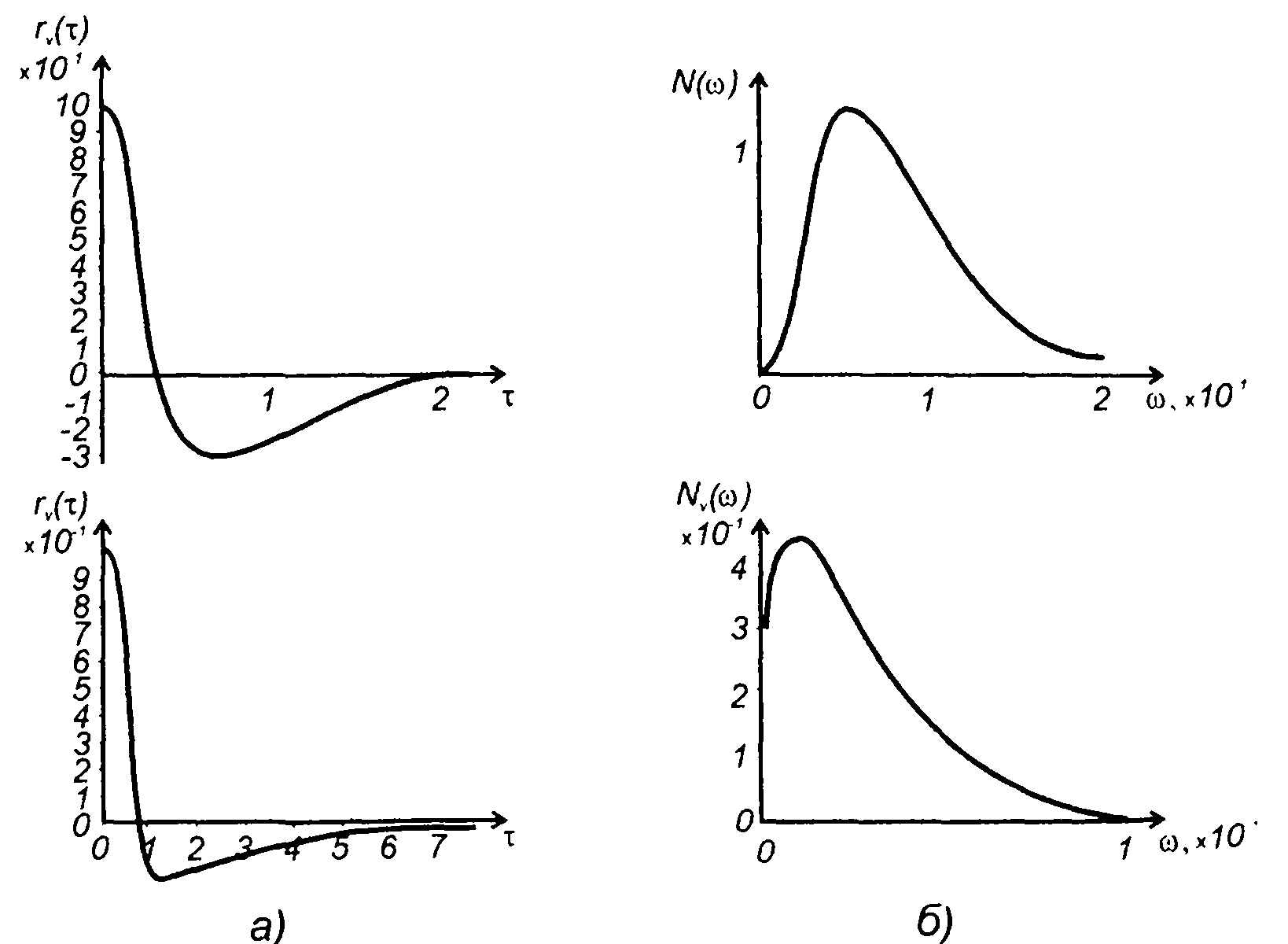
Рис. 19.24

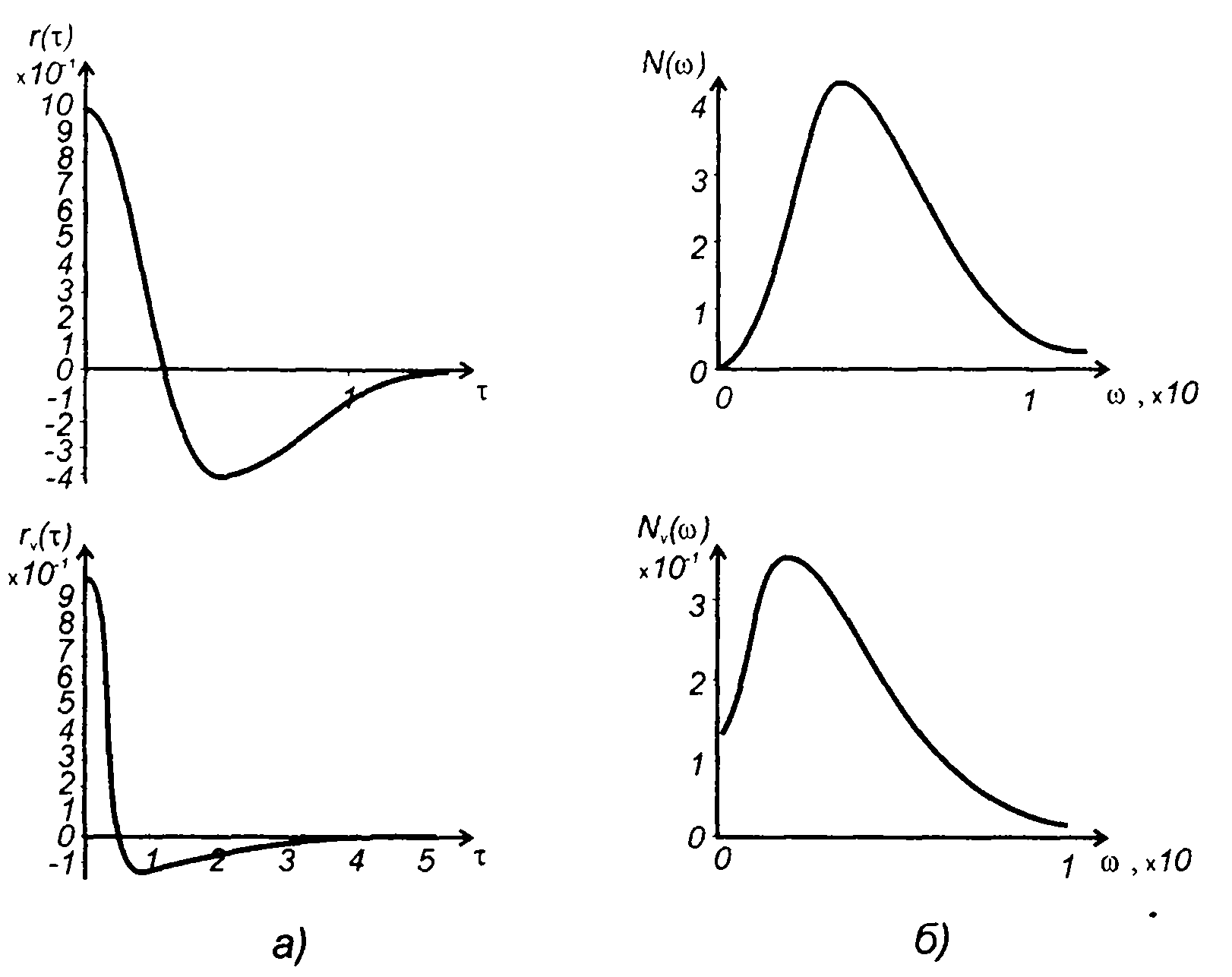
Рис. 19.25

График спектральной плотности мощности комплексной оги­бающей модулированного процесса (19.98) изображен на рис. 19.25,6.

В (19.95) раскладывая r_ξ(т) в ряд Тейлора и ограничиваясь пер­выми двумя слагаемыми, получим

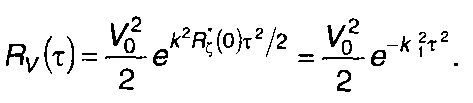(19.104)

При таком представлении R_v(т) из (19.98) найдем

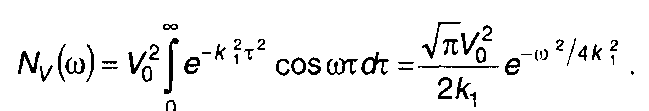(19.105)

Спектральная плотность модулированного случайного процесса

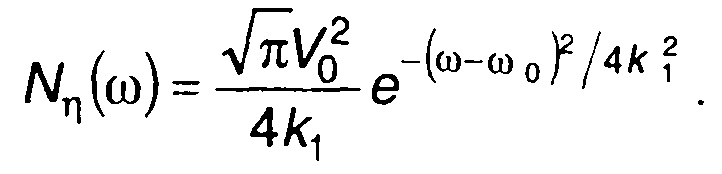(19.106)

Таким образом, спектральная плотность мощности случайного процесса, модулированного гауссовским процессом, описывается гауссовской функцией.

При малом индексе модуляции k_σξ<<1 в (19.95) можем при­нять

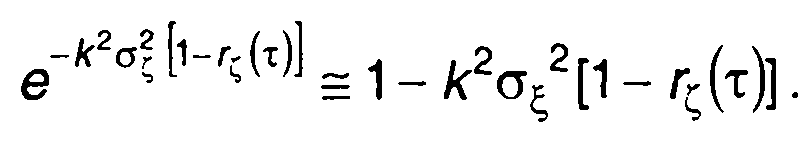(19.107)

Спектральную плотность мощности огибающей определим с ис­пользованием (19.107) и (19.103) в виде

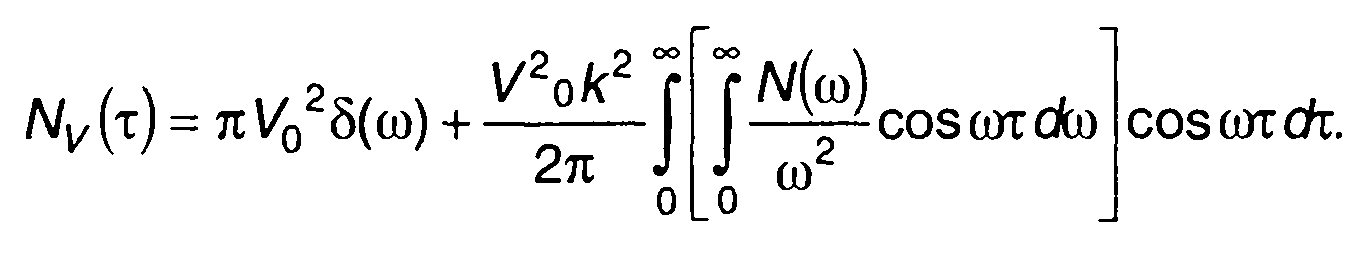(19.108)

Таким образом, при малом индексе модуляции спектральная плотность мощности комплексной огибающей ЧМ случайного про­цесса определяется спектральной плотностью мощности интегра­ла от модулирующего случайного процесса.

Раздел 20.

ВЫБРОСЫ СЛУЧАЙНЫХ ПРОЦЕССОВ

Реализация непрерывного случайного процесса представляет изменение случайной величины во времени - переходы от локаль­ного минимума к локальному максимуму и наоборот (рис. 20.1). Если установить уровень х, то можно выделить точки пересечения реализации случайного процесса с выбранным уровнем - нули и отрезки реализации над уровнем и под ним - положительные и от­рицательные выбросы случайного процесса. Анализ выбросов, их характеристик позволяет судить о поведении случайного процесса во времени.

Наиболее полной характеристикой выбросов непрерывного случайного процесса является ПРВ (ФРВ) длительности выбро­сов. Она дает возможность определить и другие, менее полные, характеристики, в частности, среднюю длительность и частоту следования выбросов, дисперсию и др. Однако несмотря на то, что подход к нахождению ПРВ длительности выбросов был пред­ложен в одной из ранних работ по теории случайных процессов [36], строгое решение задачи определения ПРВ (ФРВ) длительно­сти выбросов в общей постановке наталкивается на трудности, не всегда преодолимые на практике. Указанное обстоятельство яв­ляется причиной того, что в разделе рассматриваются несколько

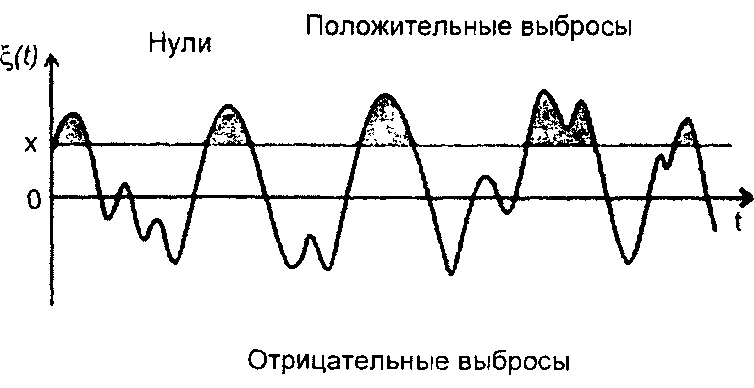
Рис.20.1

подходов к определению характеристик выбросов. Изложены наи­более простые, дающие результаты с достаточной для инженерной практики точностью.

20.1. Определение характеристик распределения длительности выбросов с использованием ФРВ случай­ного процесса

Рассмотрим стационарный случайный процесс ξ(t) на интервале времени [t, t + t]. Зададим уровень х и определим вероятность того, что при условии не превышения случайным процессом уровня х в точке t в остальных точках выделенного интервала времени он также не превышает этот уровень. Чтобы определить эту вероят­ность, разобьем интервал времени τ на n участков длительностью ∆t = τ/n.

Тогда указанная вероятность будет оцениваться как

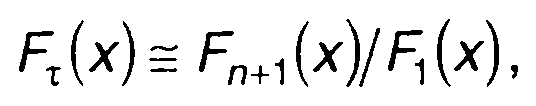(20.1)

где F_n+1(x)-(n + 1)-мерная ФРВ случайного процесса ξ(t) в моменты времени t, t + ∆t, t + 2∆t,..., t + τ.

Уменьшая длительность интервалов разбиения выбранного ин­тервала, для F_τ(x) получим следующее предельное выражение

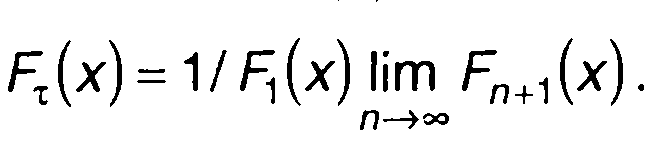(20.2)

Если значение случайного процесса ξ(t) внутри выделенного ин­тервала времени не превышает заданный уровень х, то, следова­тельно, пересечение этого уровня снизу вверх происходит только в точке вне этого интервала. Вероятность того, что случайный про­цесс не превышает уровень х на интервале х, определяет также вероятность того, что длительность отрицательных выбросов бу­дет не меньше х. Если обозначить F_-δ(τ) ФРВ длительности отри­цательных выбросов относительно уровня х, то для нее с учетом сказанного можно записать

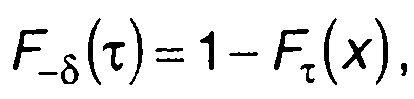(20.3)

где F_τ(x) определяется (20.2).

При невозможности получить предельное значение в (20.2) оце­нить F_-δ(τ) можно с помощью (n + 1)-мерной ФРВ случайного

процесса (20.1). Используя определение (n + 1)-мерной ФРВ через двумерную ФРВ (разд. 16), для F_T(x) запишем следующее выра­жение;

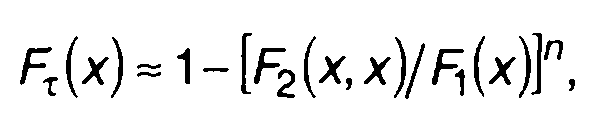(20.4)

где F₂(x,x) - двумерная ФРВ, описывающая случайный процесс

в моменты времени t и t + ∆t.

Таким образом, оценку ФРВ длительности выбросов получим в виде

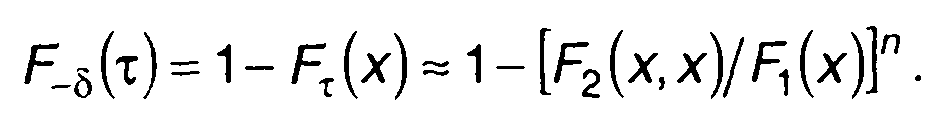
Для гауссовского процесса выражение для F_τ(x) было уточнено при n→∞.С учетом ранее полученного результата запишем

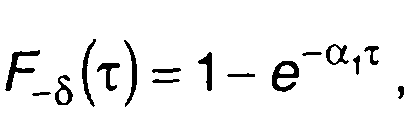(20.5)

где

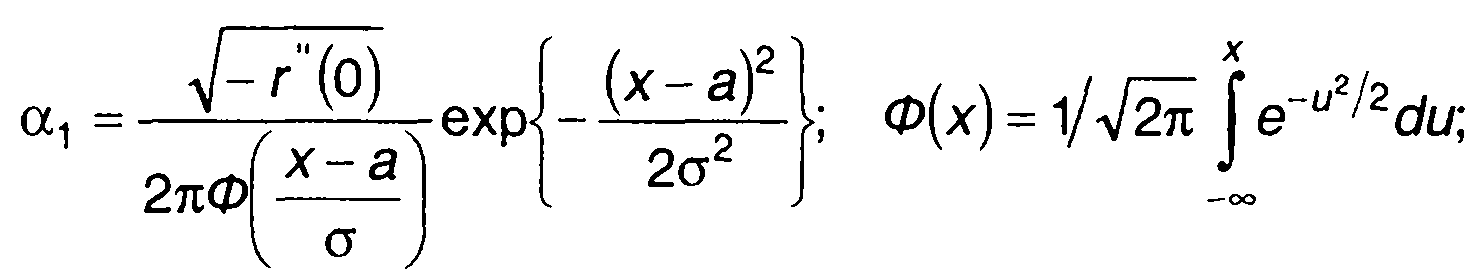(20.6)

а, σ², r(т) - математическое ожидание, дисперсия и нормированная

корреляционная функция случайного процесса ξ(t).

Аналогично получим выражение для ФРВ длительности поло­жительных выбросов

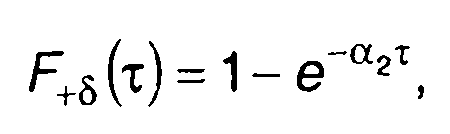(20.7)

где

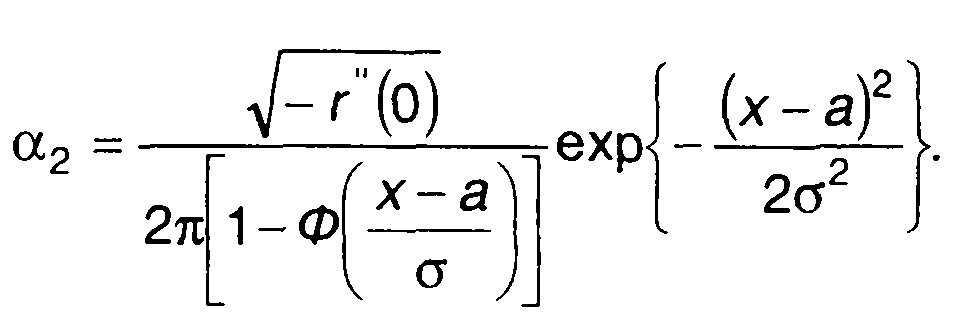(20.8)

На рис. 20.2 приведены графики ФРВ длительности выбросов: 20.2,б - отрицательных, 20.2,б - положительных как функции

обобщенного параметра √(-r"(0))τ при различных нормированных значениях уровня (х - а)/σ.

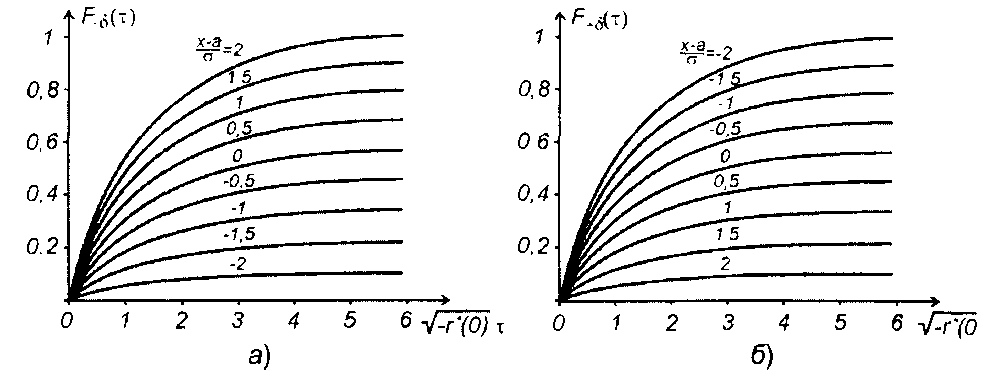
Рис. 20.2

Как следует из (20.5) - (20.8), оценка ФРВ длительности выбро­сов гауссовского процесса для нормированных значений уровня определяется второй производной нормированной корреляцион­ной функции случайного процесса при τ =0.

При определении г (о) полезно учитывать следующее соотно­шение, связывающее r" (о) со спектральной плотностью случайно­го процесса (разд. 18)

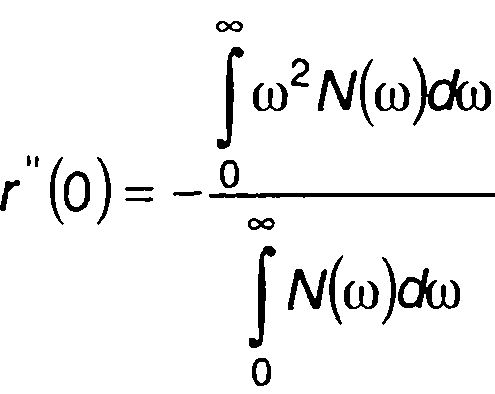(20.9)

где N(ω) - спектральная плотность мощности случайного процесса. При х = а

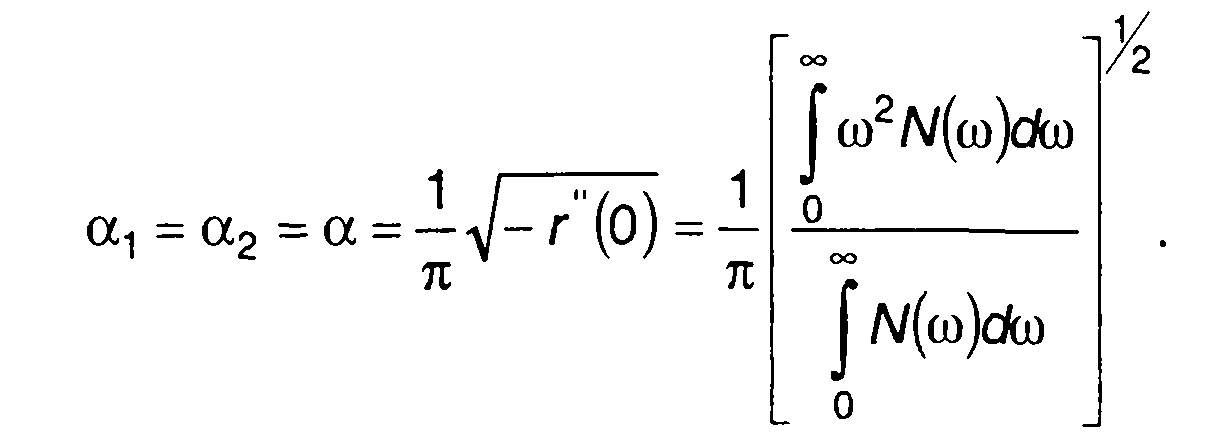
Функция распределения вероятностей длительности положи­тельных и отрицательных выбросов имеют вид:

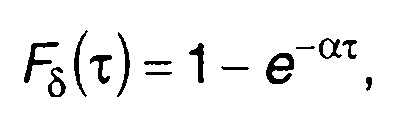(20.10)

Результат, аналогичный (20.10), получен для случайного про­цесса, имеющего распределение точек пересечения с нулевым уровнем, подчиняющееся закону Пуассона, в разд. 15. Совпадение результатов объясняется тем, что при выводе (20.2) и был сделан переход к пуассоновскому распределению нулей.

Таким образом, записано выражение для ФРВ длительности выбросов гауссовского процесса, полученное с некоторыми допу­щениями. Ошибка при расчете по нему зависит от т, ошибка уменьшается с ростом значений т.

Плотность распределения вероятностей длительности выбро­сов найдется из (20.5) и (20.7):

отрицательных выбросов

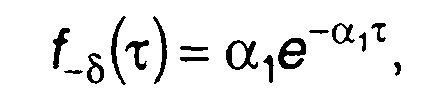(20.11)

положительных выбросов

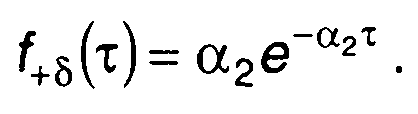(20.12)

График f_δ(τ) приведен на рис. 20.3, где а = a₁ для отрицатель­ных и а = а₂ для положительных выбросов случайного процесса.

Как следует из (20.11) и (20.12), распределение длительности выбросов, полученное при принятых допущениях, подчиняется по­казательному закону.

С учетом записанных выражений найдем математическое ожи­дание длительности выбросов, ее среднее значение

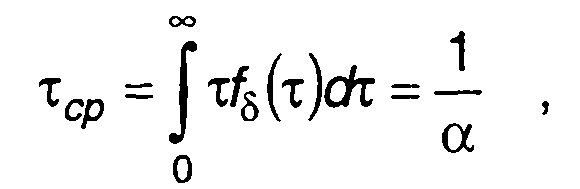(20.13)

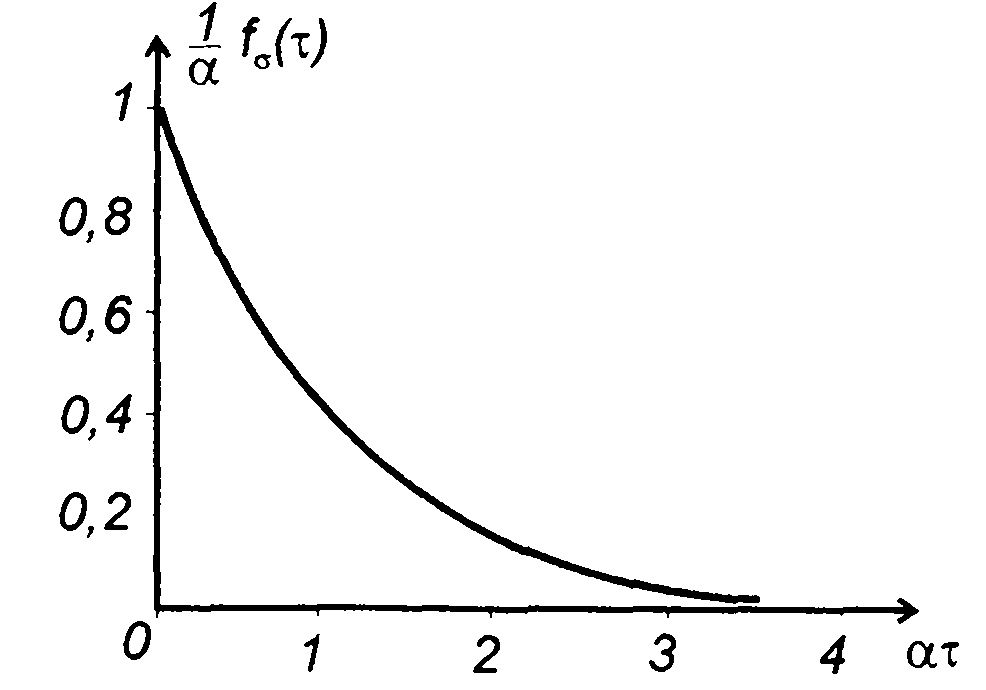
Рис. 20.3

где а = а₁ для отрицательных выбросов, а = а₂ для положительных. Таким образом, для отрицательных выбросов:

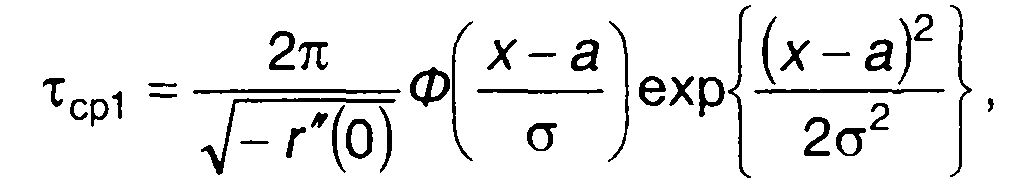(20.14)

для положительных выбросов

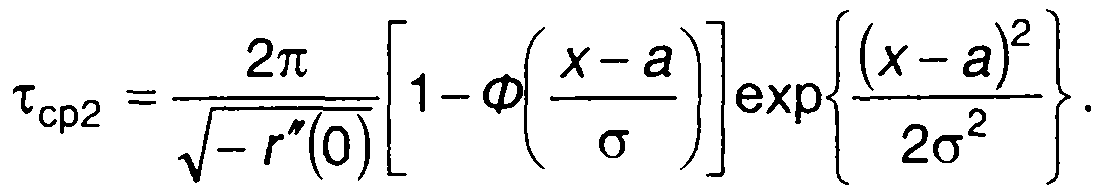(20.15)

При х = а как для отрицательных, так и для положительных вы­бросов имеем

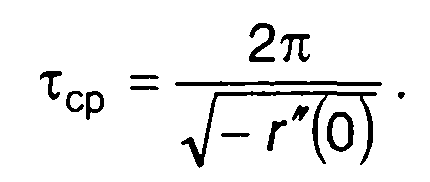(20.16)

Графики зависимости т_ср от значений уровня приведены на рис. 20.4. При увеличении значений уровня среднее значение длитель­ности отрицательных выбросов увеличивается (рис. 20.4,а), поло­жительных выбросов - уменьшается (рис. 20.4,б). Поясняют ука­занную зависимость отрезки реализаций случайного процесса, приведенные на рисунках: на рис. 20.4,а заштрихованы отрица­тельные выбросы, на рис. 20.4,б - положительные, для различных значений уровня.

С учетом (20.14) - (20.16) выражения для ФРВ и ПРВ длитель­ности выбросов можно записать в виде

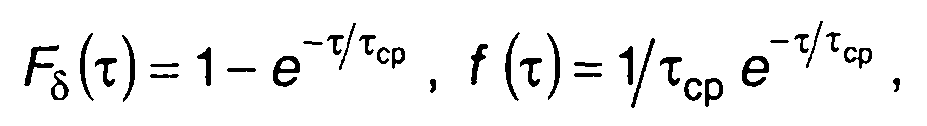(20.17)

где т_ср=т_ср1 для отрицательных выбросов (20.14), т_ср=т_ср2 для

положительных выбросов (20.15).

Сумма средних значений длительности отрицательных и поло­жительных выбросов представляет средний период их следования

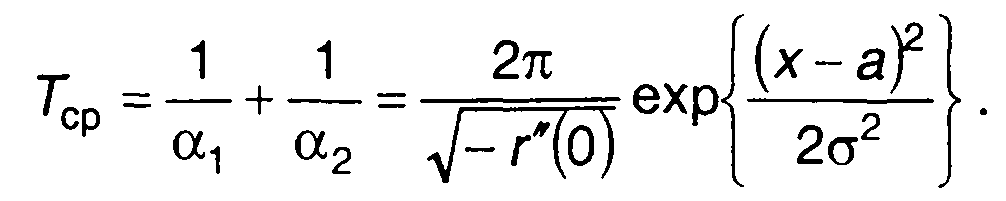(20.18)

При х = а

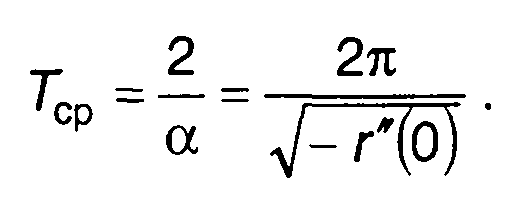
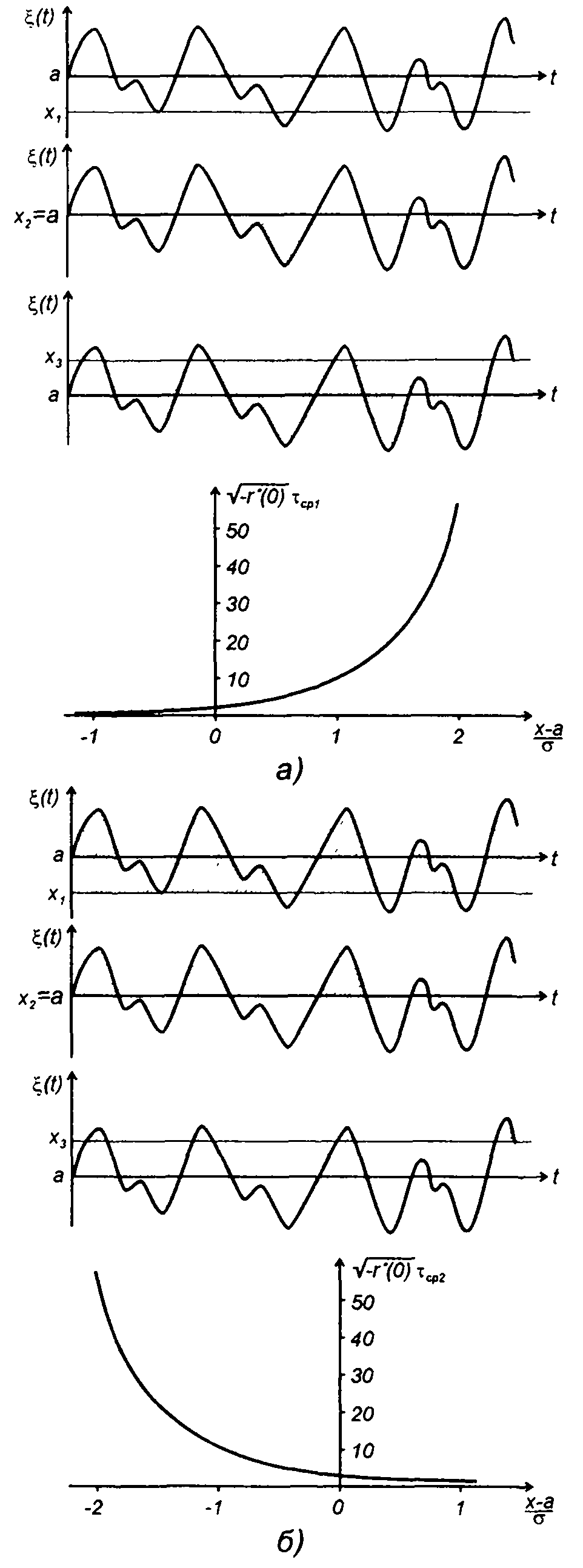
Рис. 20.4

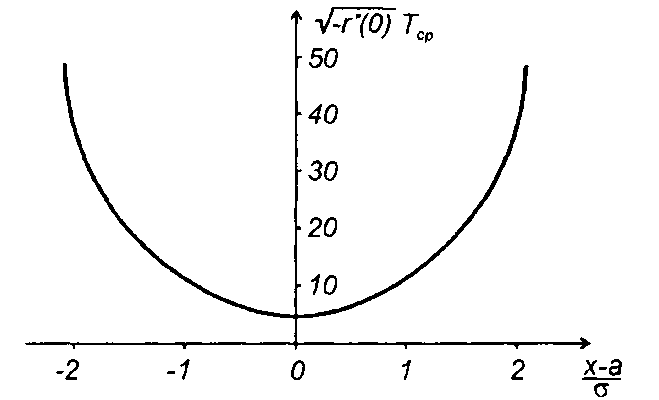
Рис. 20.5

Средняя частота следования выбросов равна

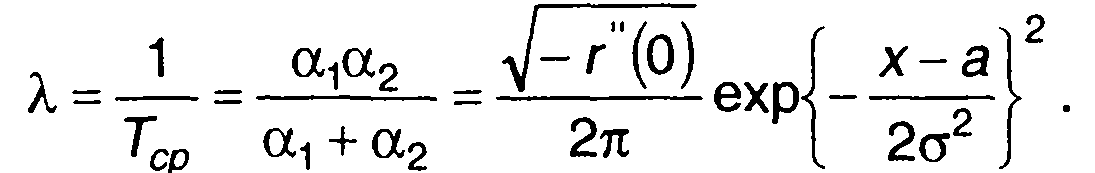(20.19)

При х = а

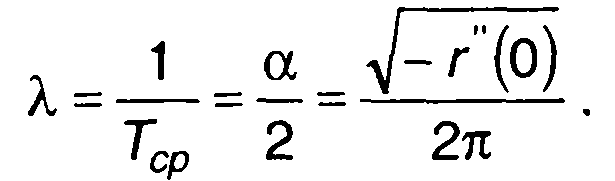(20.20)

Графики среднего значения периода и средней частоты следо­вания выбросов в зависимости от нормированного значения уров­ня приведены на рис. 20.5 и рис. 20.6.

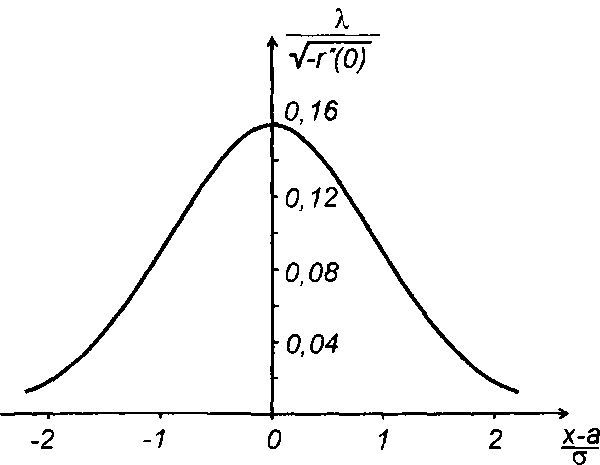
Рис. 20.6

Как следует из анализа графиков, при увеличении абсолютного значения уровня среднее значение частоты следования выбросов уменьшается, соответственно, средний период увеличивается.

Результаты (20.13) - (20.20) получены исходя из приближенных зависимостей ПРВ длительности выбросов. Однако они совпадают с полученными при строгом подхода (п. 20.3).

Выражения для средней частоты выбросов относительно мате­матического ожидания гауссовских процессов, характеристики ко­торых приведены в табл. 18.1, сведены в табл. 20.1.

Дисперсия длительности выбросов с учетом (20.10) - (20.13)

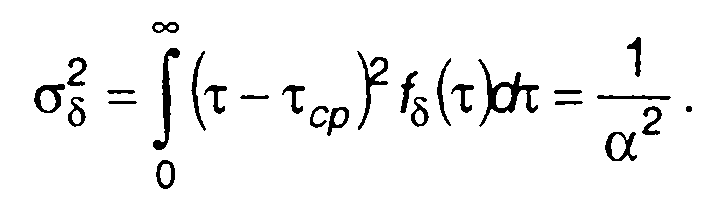(20.21)

Для отрицательных выбросов гауссовского процесса получим

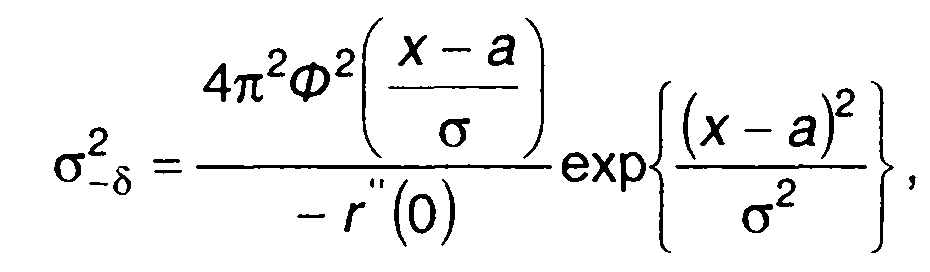(20.22)

для положительных выбросов:

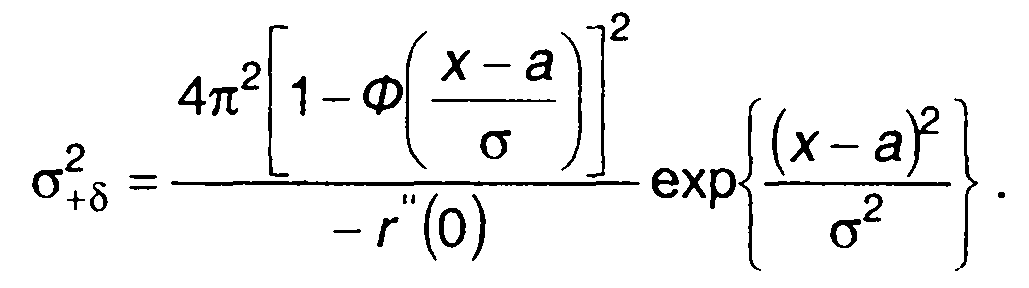(20.23)

Рассмотрим примеры характеристик распределения длительно­сти выбросов гауссовского процесса.

1. Гауссовский процесс, имеющий спектр и корреляционную функцию вида (табл. 18.1, п.1)

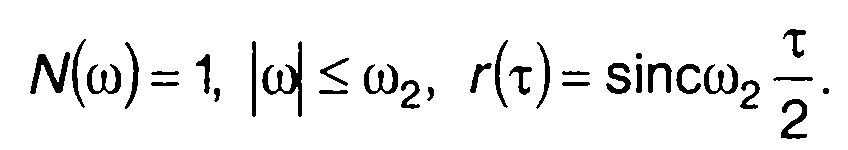
Для него получим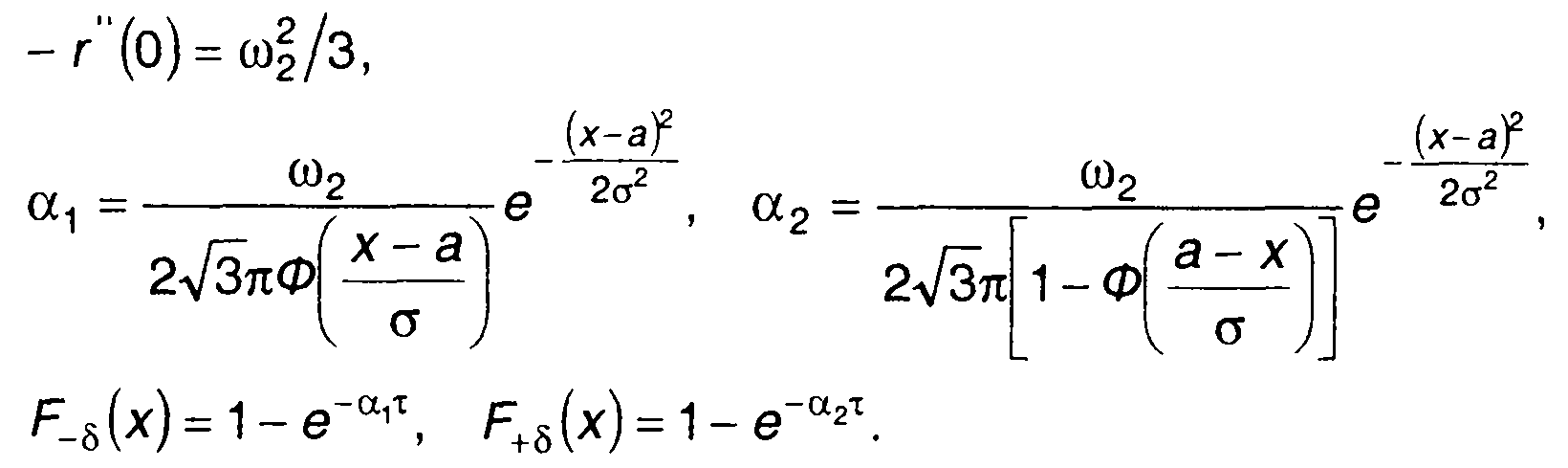

2.Гауссовский процесс, имеющий спектр и корреляционную функцию вида (табл. 18.1, п. 13)

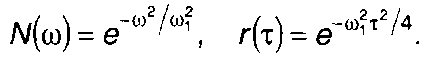
Для него получим

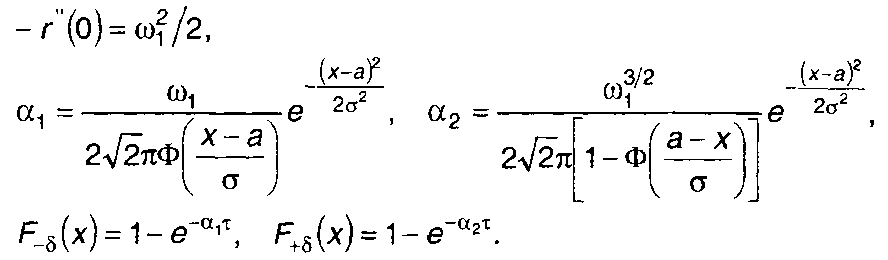
3. Гауссовский процесс, имеющий спектр и корреляционную функцию вида (табл. 18.1, п.4)

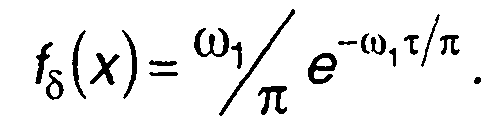
Плотность распределения вероятностей длительности выбро­сов при х = а, полученная в соответствии с (20.11) или (20.12), име­ет вид

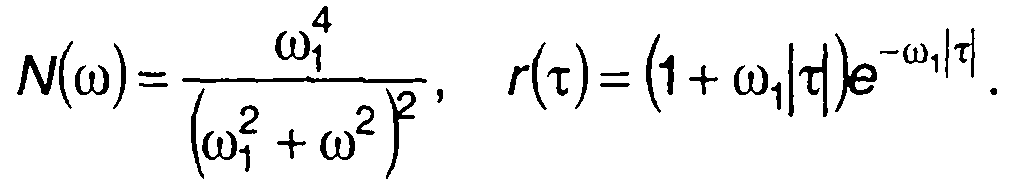
График fδ(x) изображен на рис. 20.7. На рисунке точками нанесе­ны результаты экспериментальных исследований для случайного процесса с теми же характеристиками, приведенные в [20].

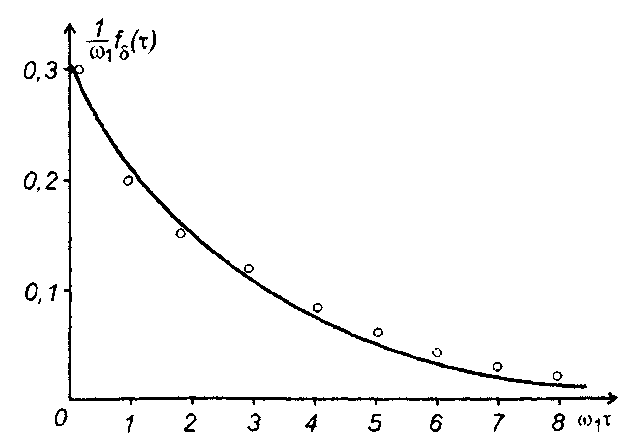
Рис. 20.7

Таблица 20.1.

Средняя частота следования выбросов гауссовского процесса

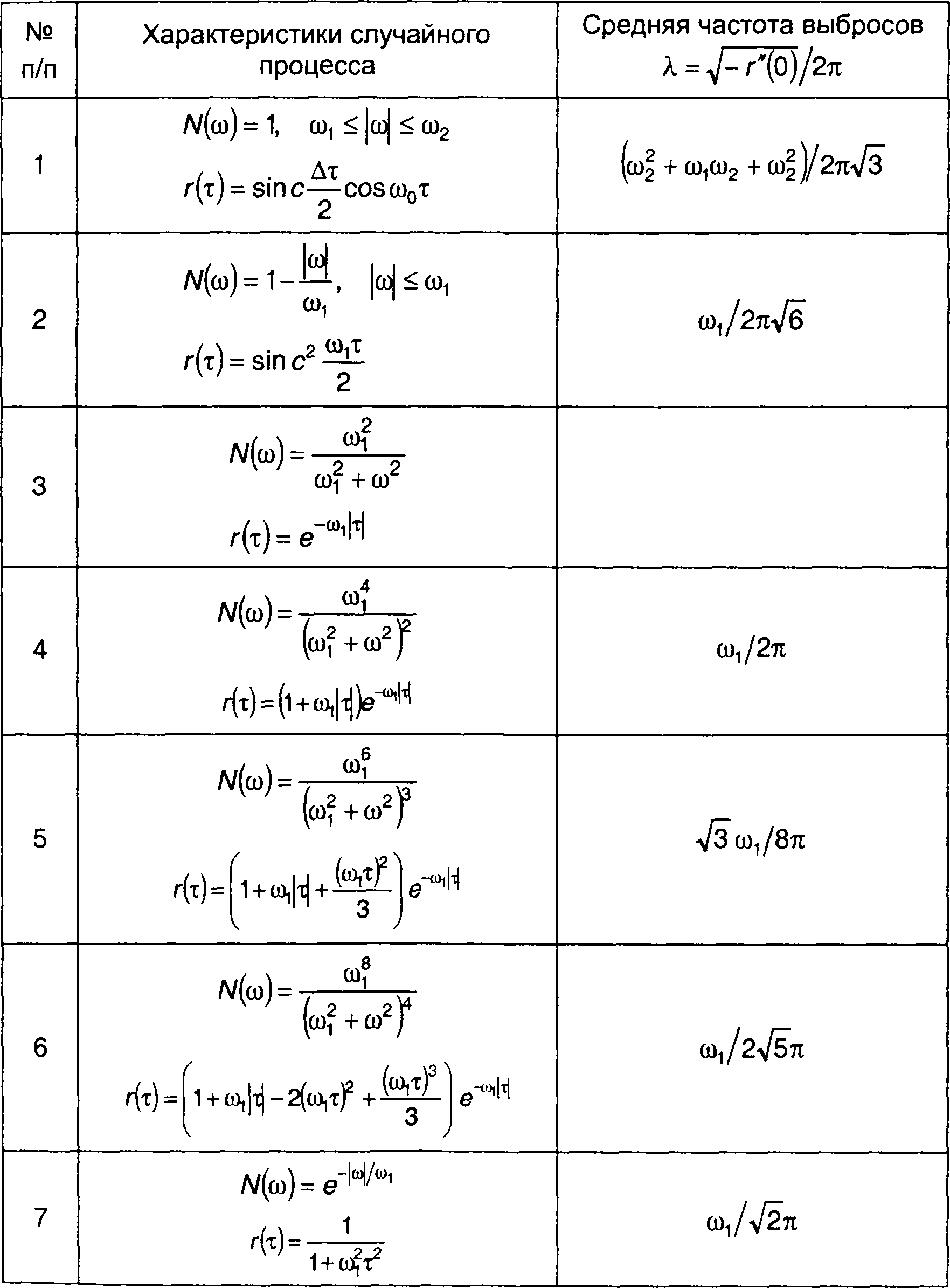
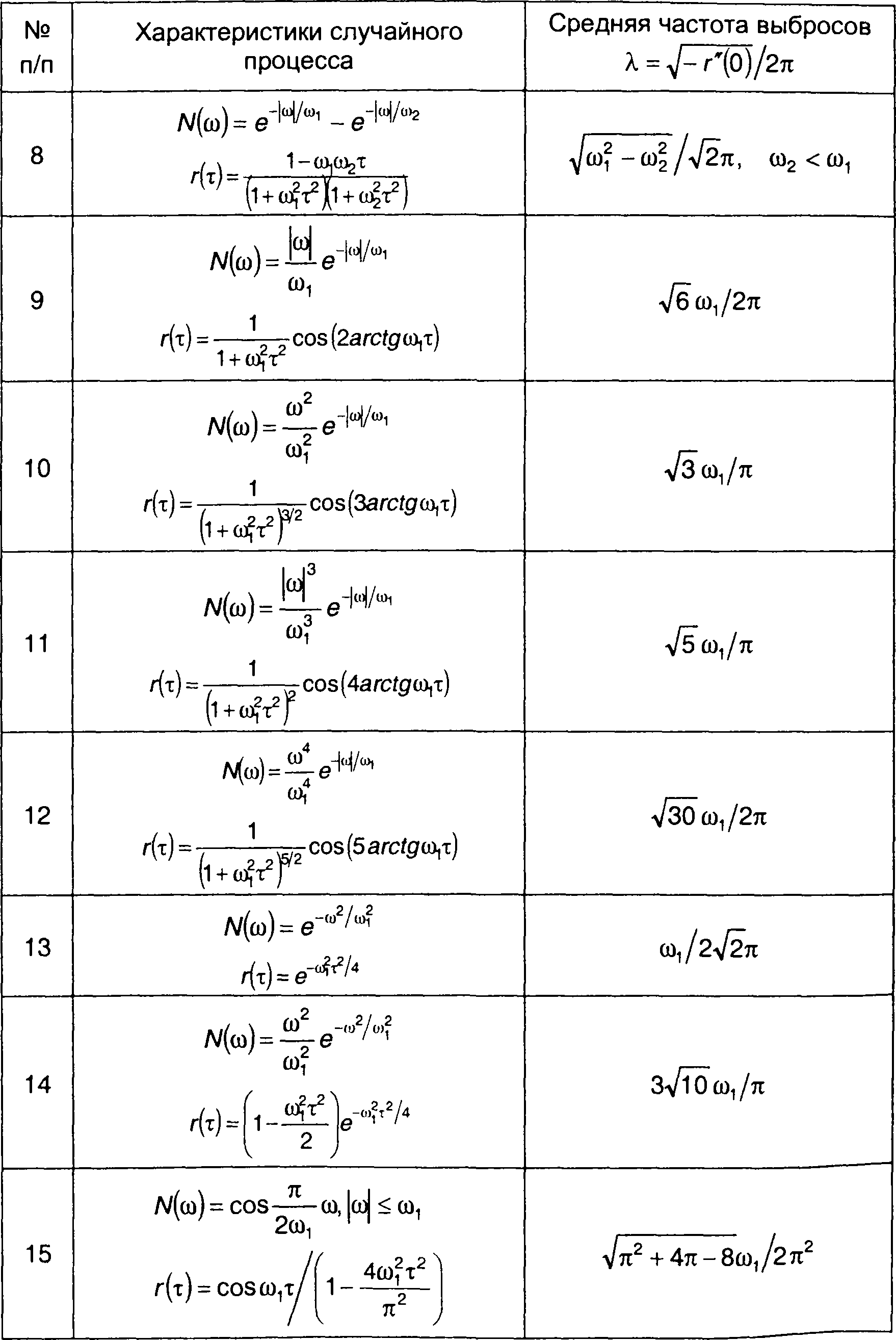
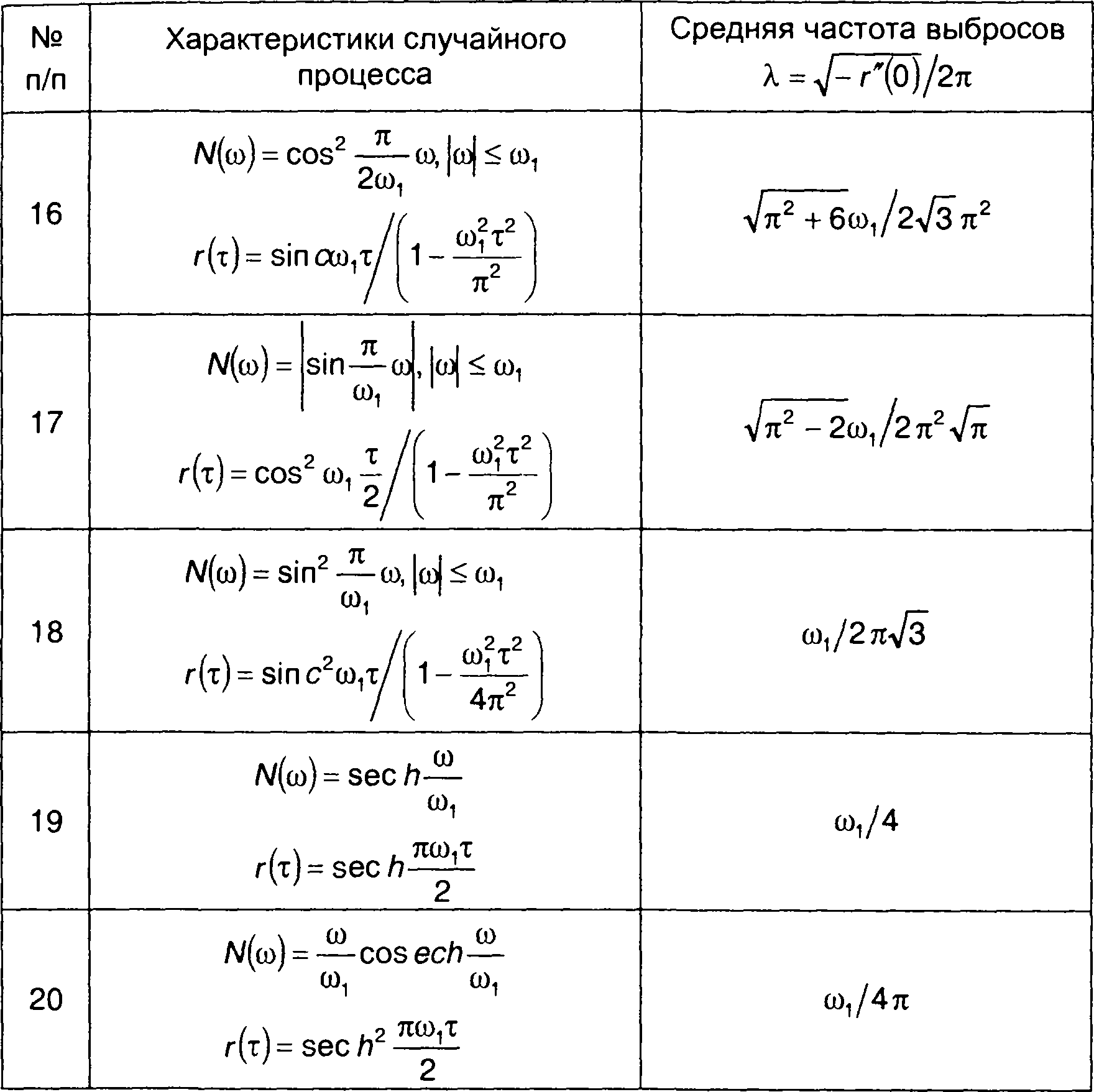
20.2. Определение характеристик распределения дли­тельности выбросов с использованием частотных ха­рактеристик случайного процесса

Прежде чем дать общую постановку задачи, рассмотрим част­ный случай распределение длительности выбросов случайного процесса с угловой модуляцией. Такое рассмотрение позволяет лучше понять и решение задачи в общем виде.

20.2.1. Распределение длительности выбросов случайного процесса с угловой модуляцией

Случайный процесс с угловой модуляцией описывается сле­дующим выражением (разд. 19)

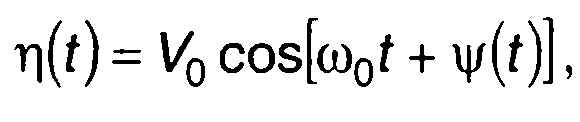(20.24)

где \/₀,ω₀,Ψ(t) - амплитуда, несущая частота и фаза сигнала.

При фазовой модуляции (ФМ)

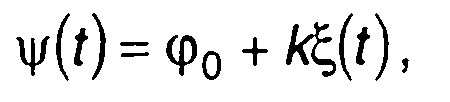
где ξ(t) - модулирующий стационарный случайный процесс; φ₀ - начальная фаза; к - коэффициент пропорциональности.

Частота ФМ сигнала

где 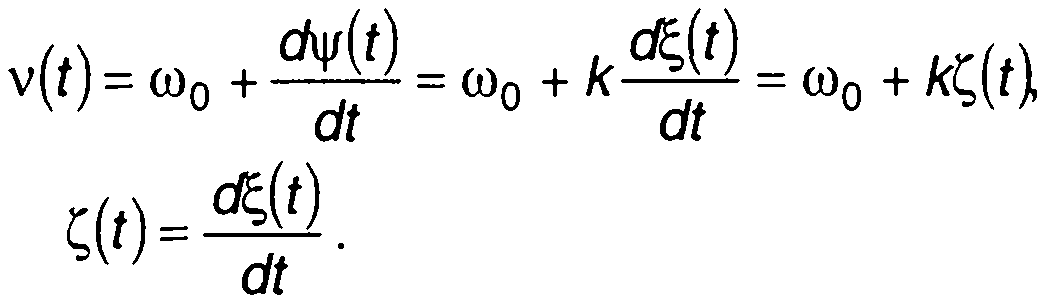(20.25)

При частотной модуляции (ЧМ) модулирующий случайный про­цесс ξ(t) воздействует непосредственно на частоту

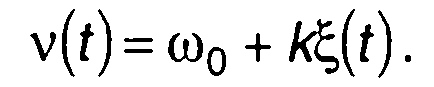(20.26)

Зная ПРВ (ФРВ) модулирующего случайного процесса ξ(t), мож­но получить ПРВ частоты модулированного процесса (разд. 19): при ФМ

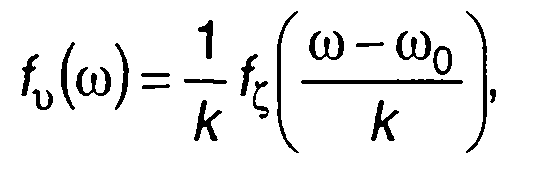(20.27)

где fζ(y) - ПРВ производной при ЧМ

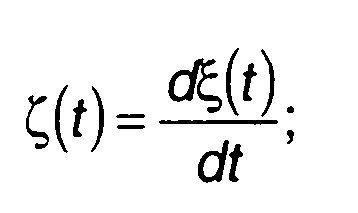
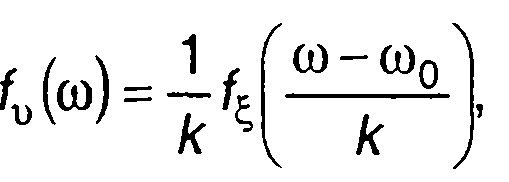(20.28)

где f^(y) - ПРВ модулирующего случайного процесса ξ(t).

Мощность модулированного случайного процесса в полосе час­тот [ω,ω+ dω] равна V02/2fu(ω)dω. Интеграл от этой величины в пределах возможного изменения частоты дает

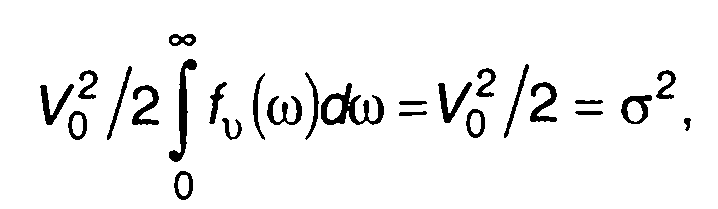(20.29)

что соответствует мощности модулированного случайного процесса.

Имея ПРВ частоты модулирующего случайного процесса, можно получить ПРВ периода следования выбросов

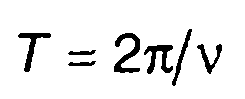(20.30)

и длительности выбросов δ

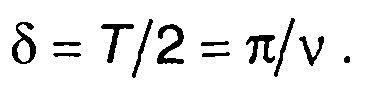(20.31)

С учетом (20.31) выражение для ПРВ длительности выбросов случайного процесса η (t) запишется в виде

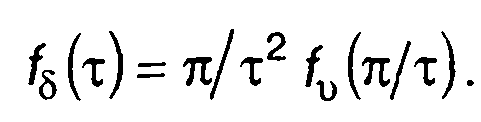(20.32)

Подставляя в (20.32) выражение для найдем ПРВ дли­тельности выбросов случайного процесса при ФМ или ЧМ.

Для гауссовского процесса ξ(t)

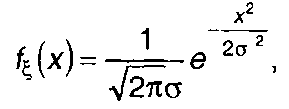(20.33)

где σ² - дисперсия ξ(t), из (20.32) при ФМ получим

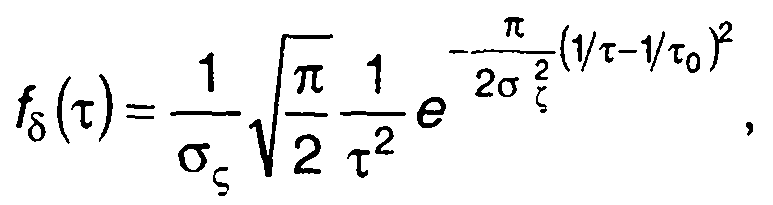(20.34)

где σ_ζ²=-k²R"(0) - дисперсия частоты; R(τ) - корреляционная функция случайного процесса ξ(t),

Используя спектральную плотность мощности модулирующего случайного процесса ξ(t), выражение для σ_ζ² запишем в виде

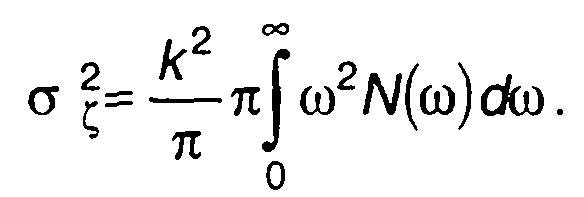(20.35)

Для ЧМ из (20.32) с учетом (20.28) получим

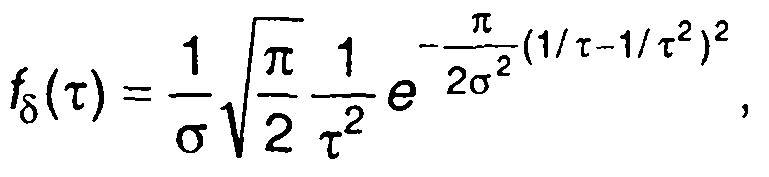(20.36)

где σ²-дисперсия случайного процесса ξ(t).

Определенный интерес представляет рассмотрение распреде­ления длительности выбросов на выходе смесителя ЧМ системы.

На вход смесителя подается ЧМ случайный процесс - непо­средственно и после задержки t₃. Случайный процесс на выходе смесителя описывается выражением

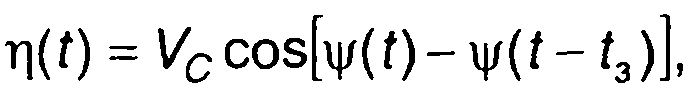(20.37)

где

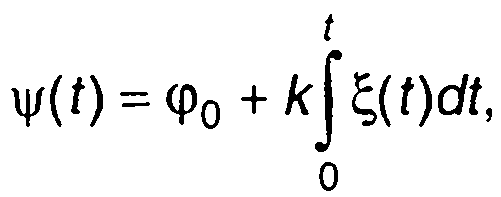
ξ(t) - модулирующий случайный процесс; t₃ - задержка.

Частота на выходе смесителя определяется как производная фазы в (20.37)

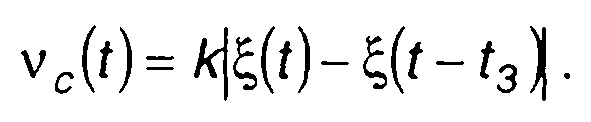(20.38)

Как следует из (20.38). несущая частота случайного процесса на выходе смесителя отсутствует. Тем не менее случайный процесс описывается выраженим, аналогичным выражению для узкополос­ного случайного процесса (20.24).

ПРВ разности ξ(f)-ξ(t- t₃) определяется выражением (разд. 17)

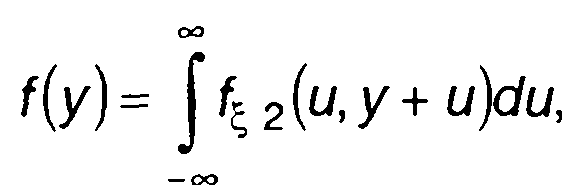(20.39)