ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 24 страница

Таким образом, для средней частоты следования максимумов слу­чайного процесса получим следующее предельное соотношение

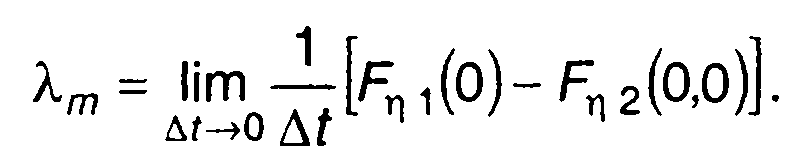(20.105)

Уточним (20.105) для гауссовского процесса ξ(t). Производная стационарного гауссовского процесса представляет гауссовский

процесс с математическим ожиданием, равным нулю, и корреляци­онной функцией, равной второй производной корреляционной функции случайного процесса со знаком минус (разд. 16). Для дву­мерной ФРВ гауссовского процесса η(t) при х = 0 по аналогии с (20.91) получим

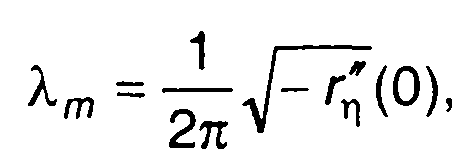(20.106)

где r_η(т) - нормированная корреляционная функция случайного процесса η(t).

С учетом того, что

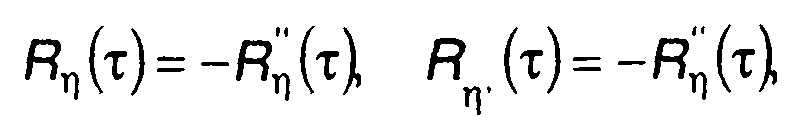(20.107)

где R(т), R_η(т), R_η (т) - корреляционные функции случайных про­цессов ξ(t); η(t) = ξ`(t), η`(t) соответственно, из (20.106) найдем

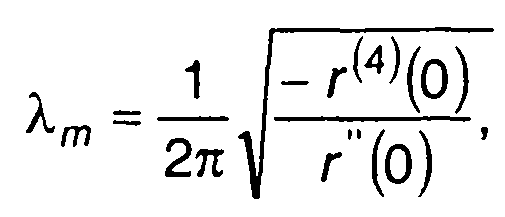(20.108)

где г⁽⁴⁾(т) - четвертая производная от нормированной корреляци­онной функции гауссовского процесса ξ(t).

Таким образом, средняя частота следования максимумов гаус­совского процесса, определяется его корреляционной функцией (значениями ее второй и четвертой производных при т = 0). Средняя частота следования минимумов случайного процесса равна средней частоте максимумов гауссовского процесса, определяется (20.108). Вывод выражения для нее аналогичен выводу выражения для Х_m.

Определяя среднюю частоту следования максимумов (миниму­мов) через среднюю частоту выбросов случайного процесса (20.81), запишем

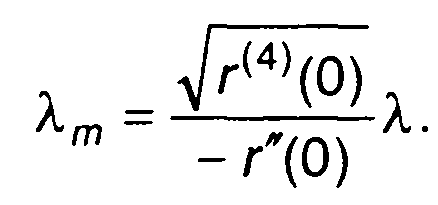(20.109)

Таким образом, средняя частота максимумов больше средней частоты выбросов в раз.

В качестве примеров рассмотрим некоторые характеристики случайных процессов.

1. Гауссовский процесс с характеристиками (табл. 18.1, п.1): спектральная плотность мощности. N(ω) = 1, ω₁ ≤ |ω| ≤ ω₂, корреляци­онная функция

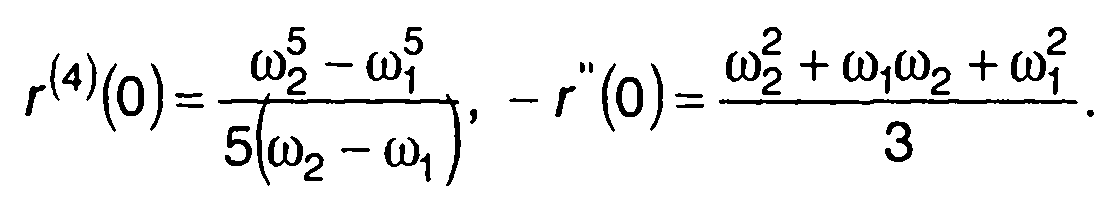
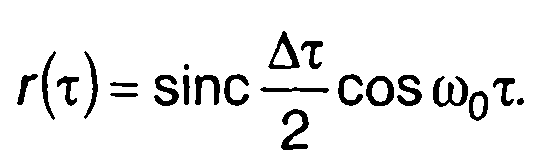
Для него имеем Из (20.103) получим

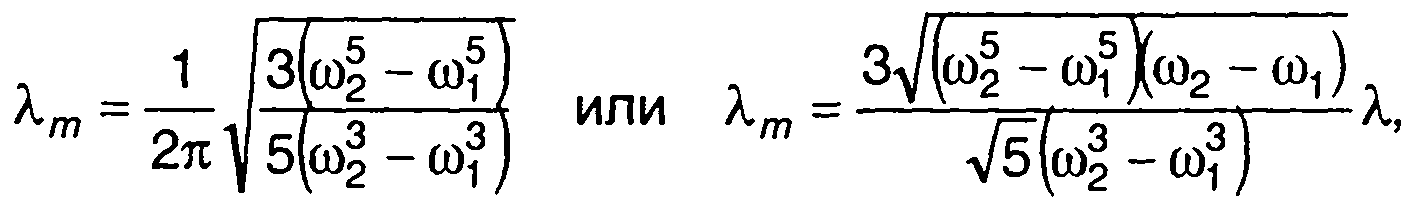
где λ - средняя частота следования выбросов.

2. Гауссовский процесс с характеристиками (табл. 18.1, п.2): спектральная плотность мощности

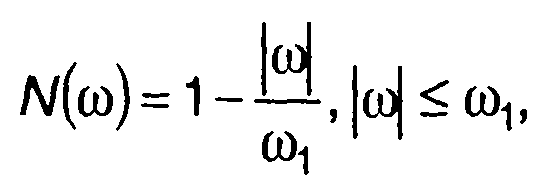
корреляционная функция

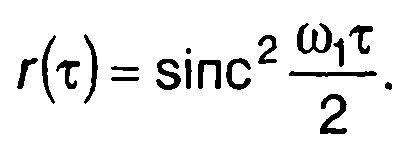
Для него имеем

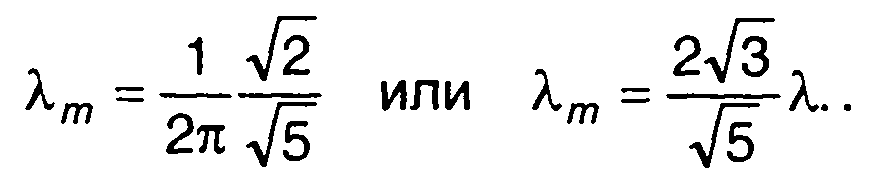
3. Гаусовский провес с характеристиками (табл. 18.1, п.5): спектральная плотность мощности

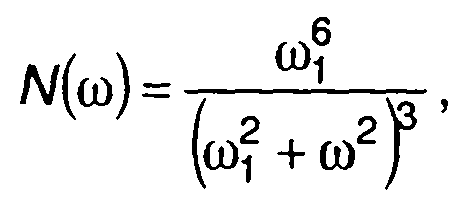
корреляционная функция

Выбросы случайных процессов

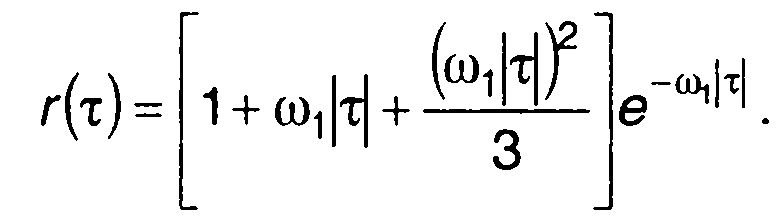
корреляционная функция

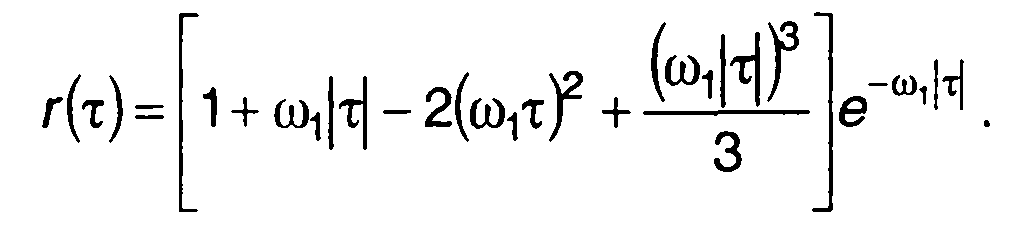
Для него имеем

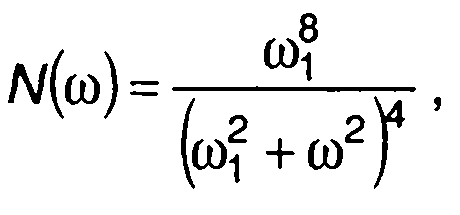
Для него имеем

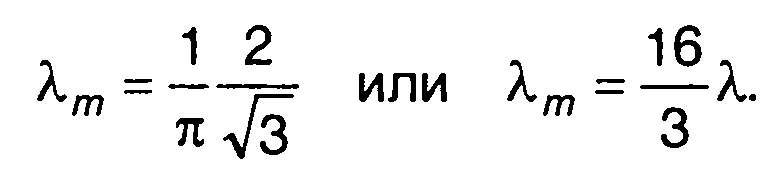
4. Гаусовский процесс с характеристиками (табл. 18.1, п.6): спектральная плотность мощности

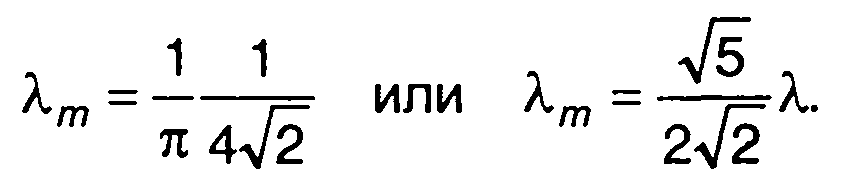
Средняя частота следования экстремумов гауссовского процес­са равна

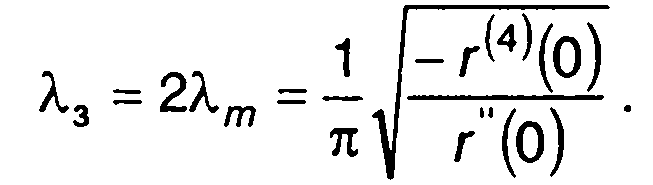(20.110)

Средний интервал между максимумами или минимумами опре­деляется как

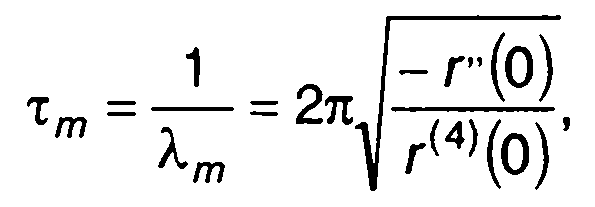(20.111)

а между экстремумами

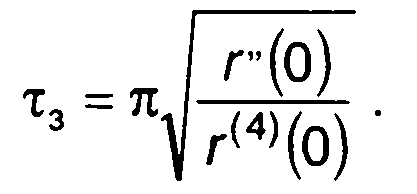(20.112)

Раздел 21.

ПРОХОЖДЕНИЕ СЛУЧАЙНОГО ПРОЦЕССА ЧЕРЕЗ ЛИНЕЙНУЮ ЦЕПЬ

Анализ прохождения случайного процесса через линейную цепь предполагает прежде всего определение характеристик случайного процесса на выходе цепи при известных характеристиках цепи и случайного процесса на входе. Методы определения основных ха­рактеристик случайного процесса на выходе линейной цепи со­ставляют содержание раздела.

21.1. Характеристики линейной цепи

Радиотехническая цепь называется линейной, если в отноше­нии нее выполняется принцип суперпозиции. Принцип суперпози­ции означает, что прохождение сигнала (колебания) через цепь не зависит от воздействия на цепь других сигналов. Результат воз­действия на цепь суммы сигналов эквивалентен сумме результатов воздействия на цепь каждого из сигналов. Цепи, для которых ука­занное условие не выполняется, называются нелинейными. Ли­нейные цепи, параметры которых изменяются, называются линей­ными параметрическими. В дальнейшем рассматриваются только линейные цепи с постоянными параметрами.

Различают временные и частотные характеристики линейных цепей, в зависимости от того, в какой области (временной или час­тотной) описываются свойства цепей. Из временных прежде всего следует отметить импульсную характеристику h(t). Она представ­ляет отклик цепи на воздействие в виде импульсной функции δ(t).При подаче на вход цепи сигнала s₁(t), сигнал на выходе опи­сывается выражением

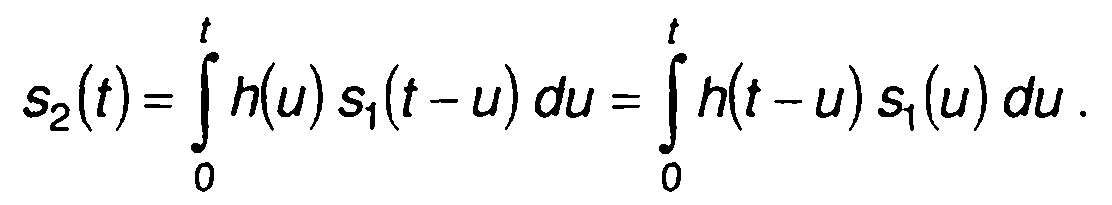(21.1)

Интеграл (21.1) называется сверткой, позволяет проводить ана­лиз прохождения сигнала через линейную цепь при известной им­пульсной характеристике цепи. Реализация случайного процесса

Прохождение случайного процесса через линейную цепь

на входе линейной цепи ξ(t) может рассматриваться как заданная функция времени. Воздействию ξ(t) соответствует отклик , реали­зация случайного процесса на выходе цепи η(t)

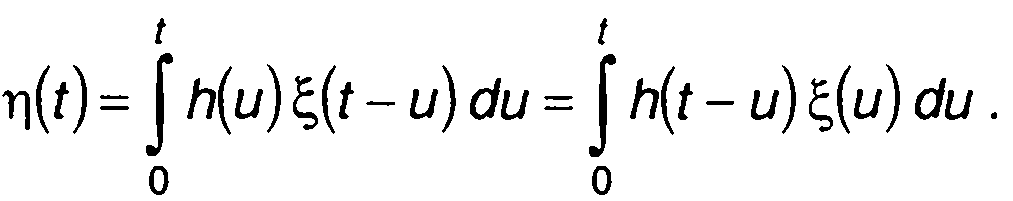(21.2)

В частотной области линейная цепь описывается комплексной частотной характеристикой. Частотная характеристика представ­ляет преобразование Фурье импульсной характеристики

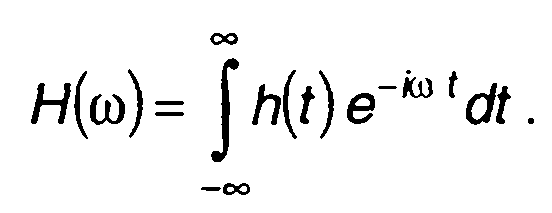(21.3)

Обратное преобразование Фурье позволяет перейти от Н(ω) к h(t)

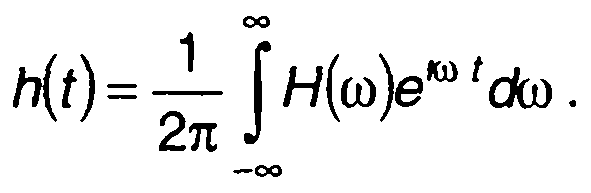(21.4)

Частотную характеристику цепи Н(ω), как комплексную величи­ну, можно представить в виде

где 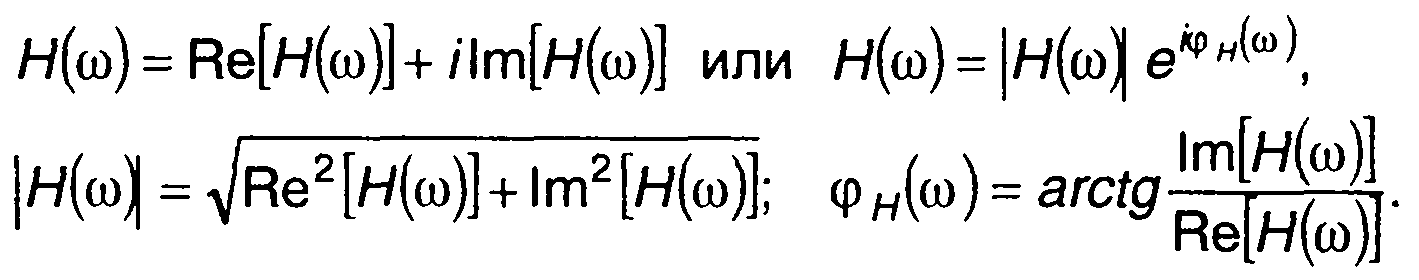(21.5)

Модуль I Н(ω)l называется амплитудно-частотной, а аргумент φ_н(ω) - фазочастотной характеристикой цепи.

Частотная характеристика цепи позволяет получить спектральную плотность мощности случайного процесса на выходе, зная спектраль­ную плотность мощности случайного процесса на входе N(ω)

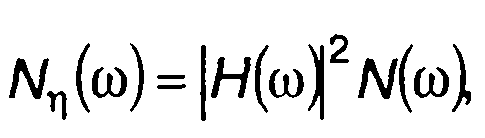(21.6)

Аналогично понятию частотной характеристики вводится поня­тие передаточной функции. Она определяется как преобразование Лапласа импульсной характеристики цепи

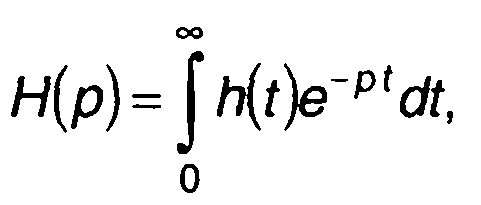(21.7)

где р = β + iω- параметр преобразования.

Ограничения, связанные с применением преобразования Лап­ласа, являются менее жесткими, чем накладываемые условиями существования преобразования Фурье. Поэтому использование преобразования Лапласа расширяет рамки анализа прохождения сигналов через линейные цепи.

Приведенные характеристики линейной цепи позволяют прово­дить анализ прохождения сигналов через линейные цепи во вре­менной и частотной областях. Выражения (21.2) и (21.6) связывают случайные процессы и их спектры на входе и выходе линейной це­пи. Они чаще всего и используются при определении характери­стик случайного процесса на выходе цепи при известных характе­ристиках случайного процесса на входе.

21.2. Распределение вероятностей случайного процесса на выходе линейной цепи

Наиболее полной характеристикой случайного процесса является ФРВ или ПРВ. Задача определения ФРВ или ПРВ случайного про­цесса на выходе линейной цепи при известных характеристиках слу­чайного процесса на входе должна рассматриваться одной из ос­новных при анализе прохождения случайного процесса через цепь.

Если случайный процесс на входе является гауссовским, то процесс на выходе будет также гауссовским. Этот вывод следует из того положения, что любые линейные преобразования нормаль­но распределенной случайной величины не меняют ее закона рас­пределения вероятностей. ФРВ или ПРВ стационарного гауссов­ского процесса описываются математическим ожиданием и корре­ляционной функцией. Поэтому для описания прохождения гауссов­ского процесса через линейную цепь достаточно определить мате­матическое ожидание и корреляционную функцию случайного про­цесса на выходе цепи.

Если линейная цепь является узкополосной, то при подаче на ее вход широкополосного случайного процесса с любым законом распределения, на выходе цепи происходит нормализация случай­ного процесса - его распределение приближается к нормальному. Явление нормализации случайного процесса на выходе узкополос­ной цепи является следствием центральной предельной теоремы теории вероятностей. Пояснить это положение помогает анализ выражения (21.2). Оно может рассматриваться как предельное дискретной свертки h(t) и ξ(t)

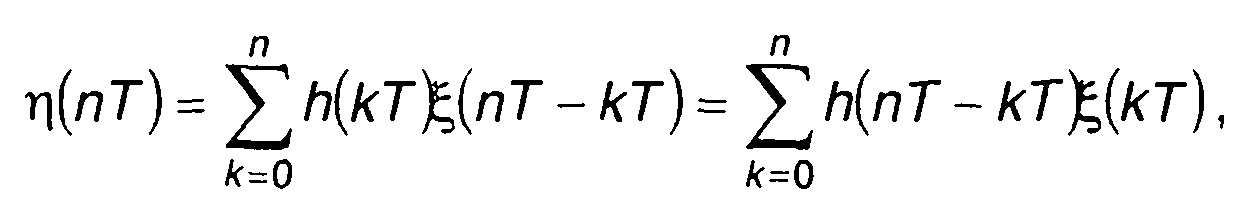(21.8)

Прохождение случайного процесса через линейную цепь

где Т - интервал дискретизации, Т≤π/ω_m; ω_m - предельная

частота спектра случайного процесса ξ(t).

Чем более узкополосной является линейная цепь, тем большее число слагаемых в (21.9) имеет достаточно большой вес и должно учитываться при расчете. Число учитываемых слагаемых при за­данной характеристике цепи h(t) будет и тем больше, чем меньше интервал Т, следовательно, чем более широкую полосу занимает спектр случайного процесса (ω_m). При увеличении же числа сла­гаемых распределение их суммы стремится к нормальному (цен­тральная предельная теорема теории вероятностей).

В общем случае задача нахождения распределения случайного процесса на выходе линейной цепи при произвольном законе рас­пределения вероятностей случайного процесса на входе является довольно сложной. Из возможных подходов к ее решению остано­вимся на подходе, основанном на определении моментов распре­деления вероятностей случайного процесса на выходе цепи. От моментов распределения вероятностей можно перейти к характе­ристической функции и ПРВ случайного процесса (разд. 15).

Начальный момент n-го порядка случайного процесса на выходе линейной цепи η(t) определяется с учетом (21.4) выражением

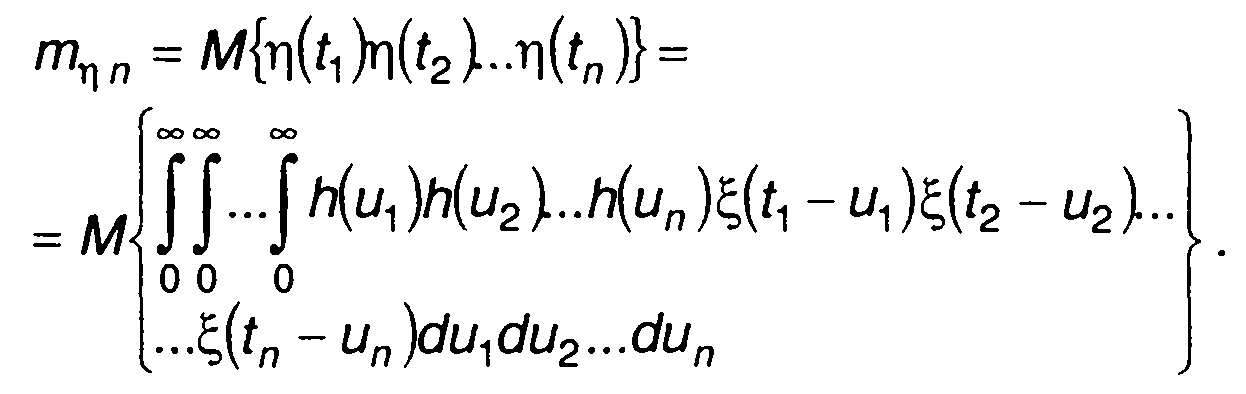(21.9)

Меняя порядок усреднения и интегрирования, запишем

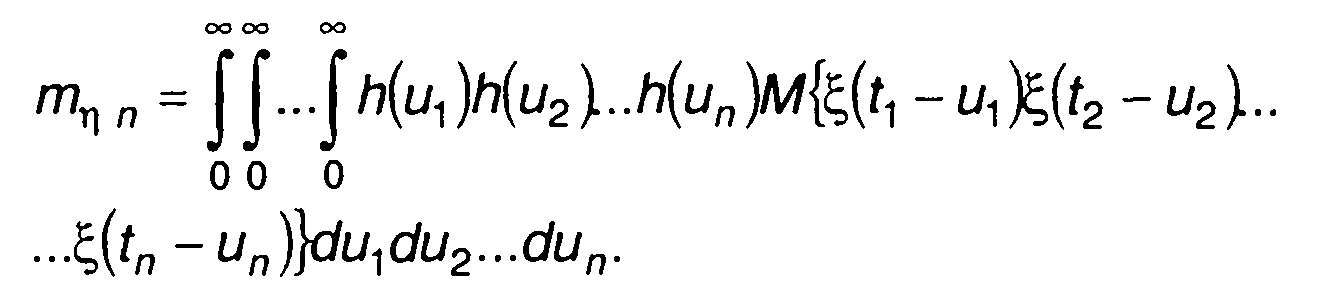(21.10)

Таким образом, для определения момента m_ηn необходимо

знать момент распределения вероятностей n-го порядка случайно­го процесса на входе цепи. Ограничиваясь знанием одномерной ФРВ (ПРВ) случайного процесса на входе цепи и получением с ее помощью начальных моментов порядка до п включительно, выра­жение для л-мерного начального момента случайного процесса на выходе цепи запишем в виде

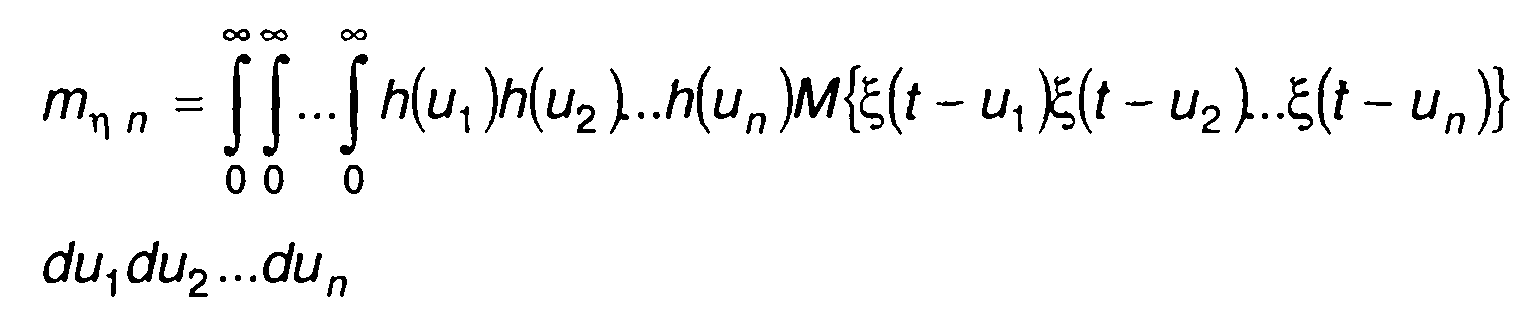(21.11)

Используя моменты распределения, определяемые (21.11), мо­жем записать выражение для одномерной характеристической функции случайного процесса на выходе r\(t)

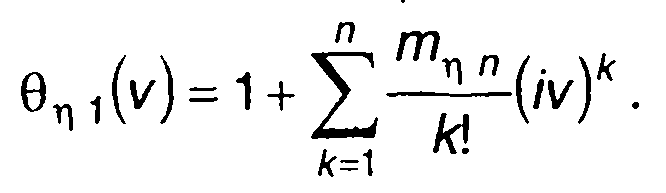(21.12)

От характеристической функции перейдем к ПРВ случайного процесса

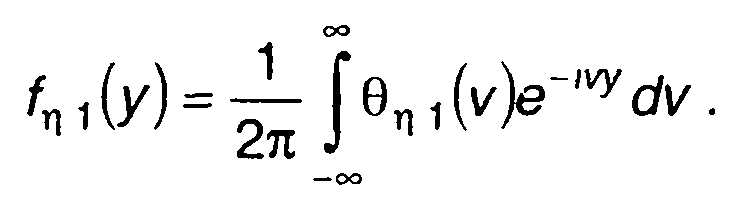(21.13)

Чем больше известно моментов распределения, тем точнее по­лучим характеристическую функцию и ПРВ случайного процесса на выходе цепи η(t). Анализ приведенных выражений в рамках ре­шаемой задачи, а также выражений для моментов наиболее часто встречающихся распределений вероятностей (табл. 2.2) показыва­ет, что описанный подход к нахождение распределения случайного процесса на выходе линейной цепи является сложным, часто не­приемлемым на практике. Отмеченное обстоятельство является причиной того, что при анализе случайного процесса на выходе линейной цепи часто ограничиваются определением математиче­ского ожидания и корреляционной функции (или спектральной плотности мощности). При этом берется во внимание, что указан­ные характеристики гауссовского процесса полностью его описы­вают, а нормальное распределение случайного процесса на выхо­де линейной цепи - довольно распространенный случай.

21.3. Математическое ожидание и корреляционная функ­ция случайного процесса на выходе линейной цепи

Математическое ожидание случайного процесса на выходе ли­нейной цепи при подаче на вход стационарного случайного про­цесса определяется выражением

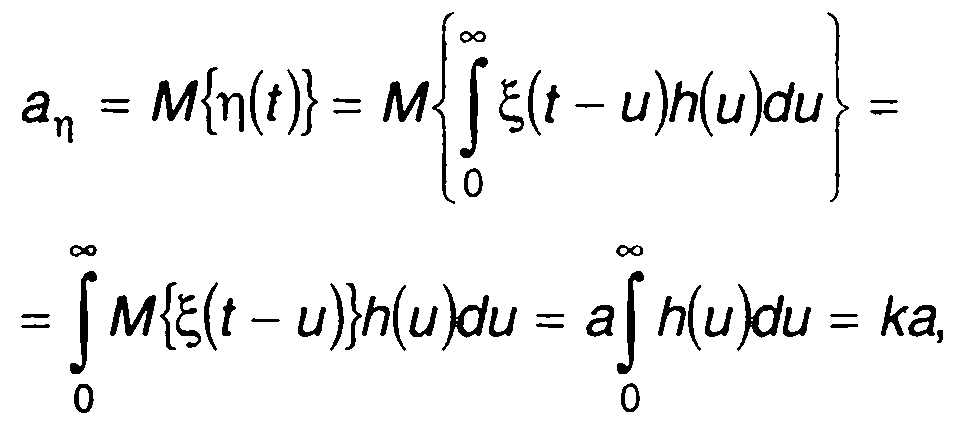(21.14)

где а - математическое ожидание случайного процесса на входе цепи ξ(t)\ h(t) - импульсная характеристика линейной цепи;

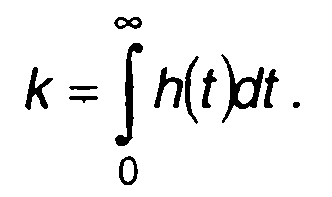(21.15)

Как следует из (21.14), математическое ожидание случайного процесса на выходе линейной цепи пропорционально математиче­скому ожиданию случайного процесса на входе.

Выражение для ковариационной функции случайного процесса на выходе линейной цепи запишем в виде

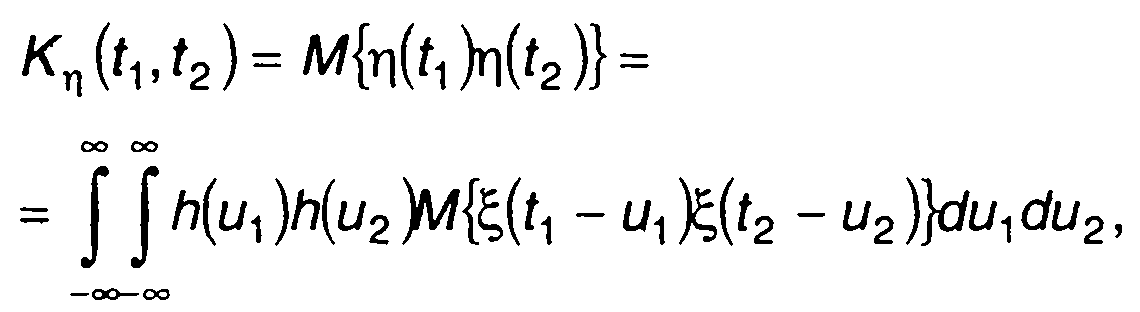(21.16)

где h(t) определено для t ≥0.

Если случайный процесс на входе ξ(t) является стационарным, то (21.16) примет вид

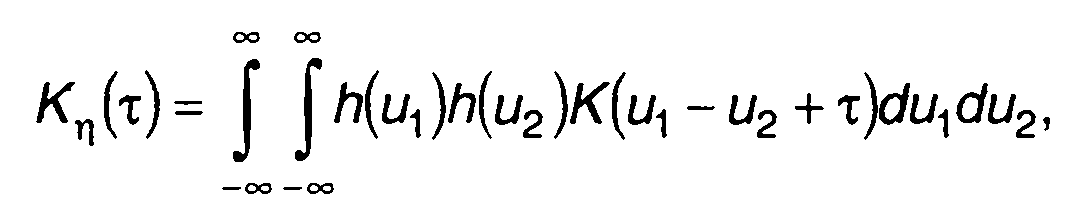(21.17)

где К(τ) - ковариационная функция случайного процесса на входе

ξ(t), т = t₂ — t₁.

Переходя в (21.27) от переменных u₁ и и₂ к и = u₁ и v = u₂-u, запишем

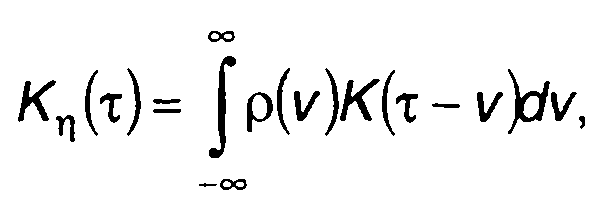(21.18)

где

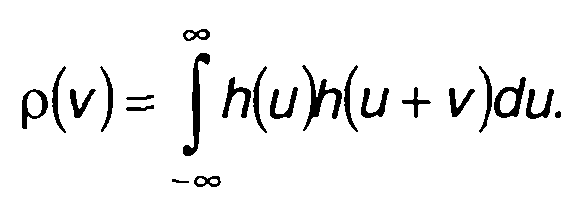(21.19)

Таким образом, ковариационная функция случайного процесса на выходе линейной цепи определяется сверткой К(τ) и p(т). Ино­гда р(τ) рассматривают как автокорреляционную функцию им­пульсной характеристики цепи.

Для центрированного случайного процесса на входе К(τ) = R(т)

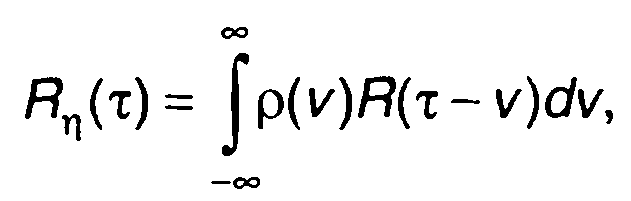(21.20)

где R(т) - корреляционная функция случайного процесса на входе. Дисперсия случайного процесса на выходе цепи равна

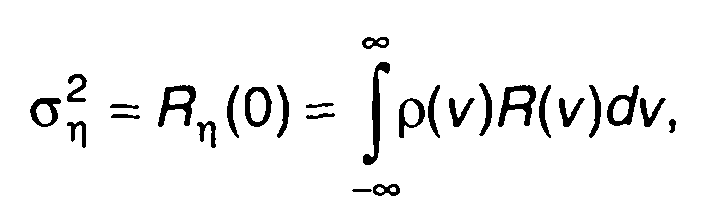(21.21)

Нормированная корреляционная функция

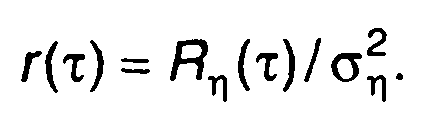(21.22)

При воздействии на линейную цепь белого шума, имеющего корреляционную функцию в виде импульсной функции (разд. 18)

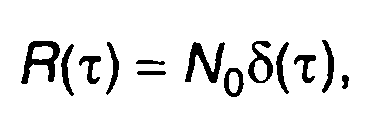(21.23)

корреляционная функция случайного процесса на выходе цепи описывается выражением

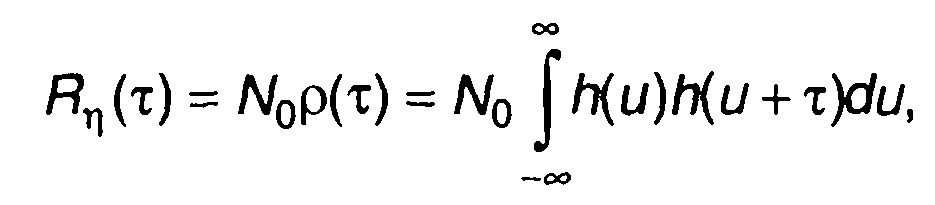(21.24)

определяется автокорреляционной функцией импульсной характе­ристики цепи р(т).

Так автокорреляционная функция импульсной характеристики RС-цепи (табл.18.1, п. 1) h(t) = be~^bt имеет вид (т > 0)

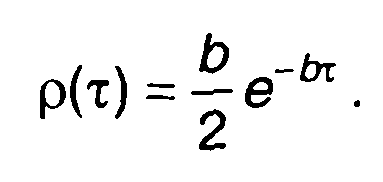
При подаче на вход такой цепи белого шума корреляционная функция случайного процесса на выходе определяется из (21.24) как

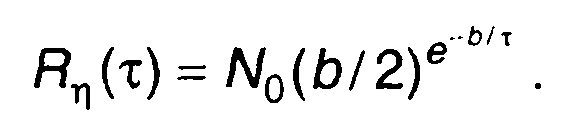
При решении (21.20) наибольшую сложность, пожалуй, пред­ставляет определение пределов интегрирования.

Взаимная корреляционная функция центрированного случайно­го процесса на входе ξt) и выходе η(t) линейной цепи определяет­ся выражением

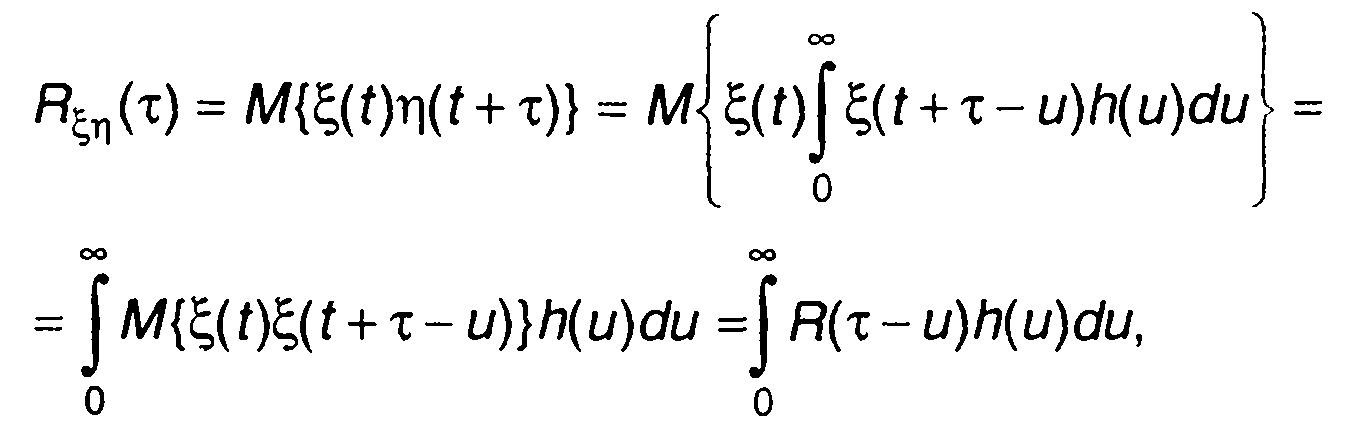(21.25)

где R(т) - корреляционная функция случайного процесса на входе.

Как следует из (21.25), взаимная корреляционная функция оп­ределяется сверткой корреляционной функции случайного процес­са на входе и импульсной характеристики цепи.

Изменяя порядок следования функций ξ(t) и η(t), получим

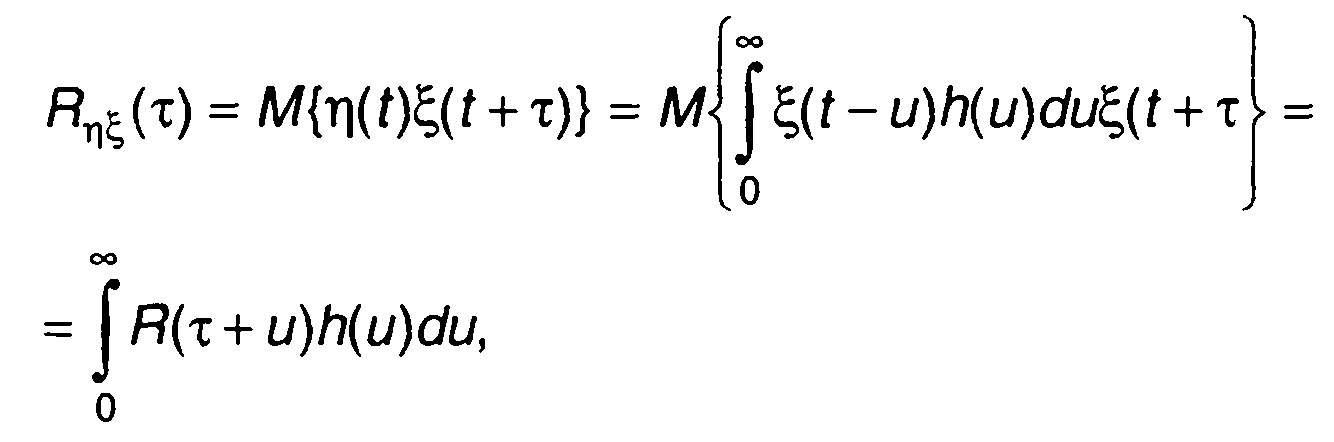(21.26)

Как следует из сравнения (21.25) и (21.26), R_ξη(т) ≠ R_ηξт) .

При воздействии на линейную цепь белого шума ξ(t), имеющего корреляционную функцию R(т) = R(0)δ(т), из (21.30) получим

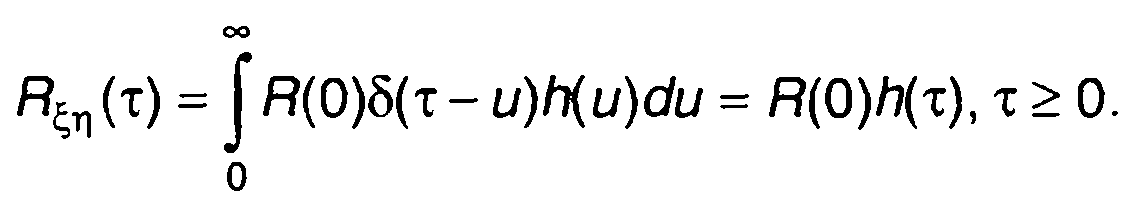(21.27)

Таким образом, взаимная корреляционная функция в этом слу­чае пропорциональна импульсной характеристике цепи.

21.4. Спектр случайного процесса на выходе линейной цепи

Имея корреляционную функцию случайного процесса на выходе цепи, можно получить его спектральную плотность мощности. Од­нако часто для ее получения удобнее проводить анализ полностью в частотной области.

Выделим отрезок реализации центрированного случайного про­цесса ξ(t) на входе линейной цепи, имеющей импульсную h(t) и частотную Н(ω) характеристики. Спектральные плотности сигнала на выходе и входе цепи связаны соотношением

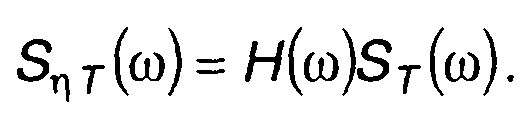(21.28)

От (21.28) можем перейти к следующему равенству

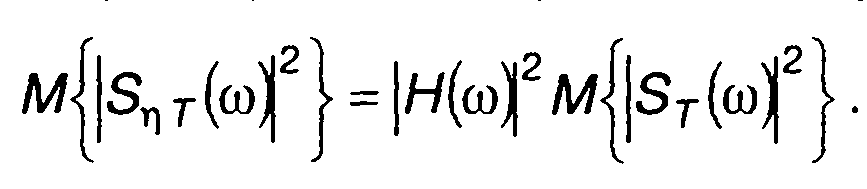(21.29)

Из (21.29) непосредственно следует

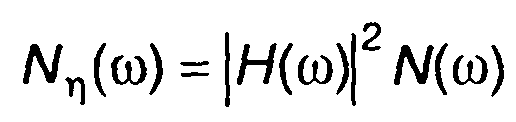(21.30)

Таким образом, спектральная плотность мощности случайного процесса на выходе линейной цепи равна произведению квадрата модуля частотной характеристики цепи и случайной плотности мощности случайного процесса на входе.

Во временной области произведению (21.30) соответствует свертка временных функций. Учитывая, что во временной области |H(ω)| соответствует корреляционная функция импульсной харак­теристики р(т), a N(ω) - корреляционная функция случайного про­цесса на входе R(τ), можем записать

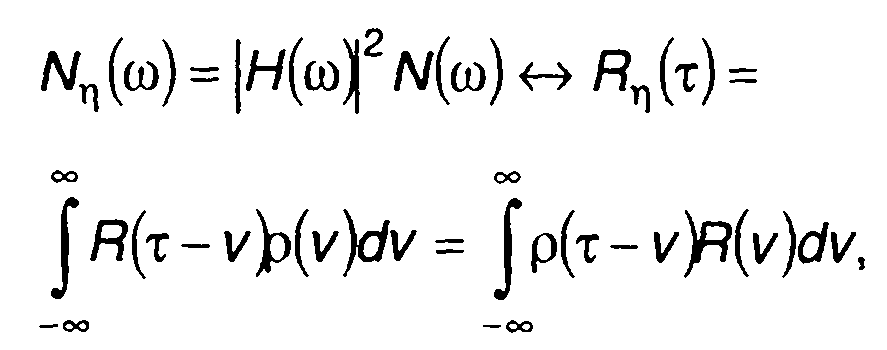(21.31)

где символ <—>означает соответствие по Фурье, что совпадает с (21.20).

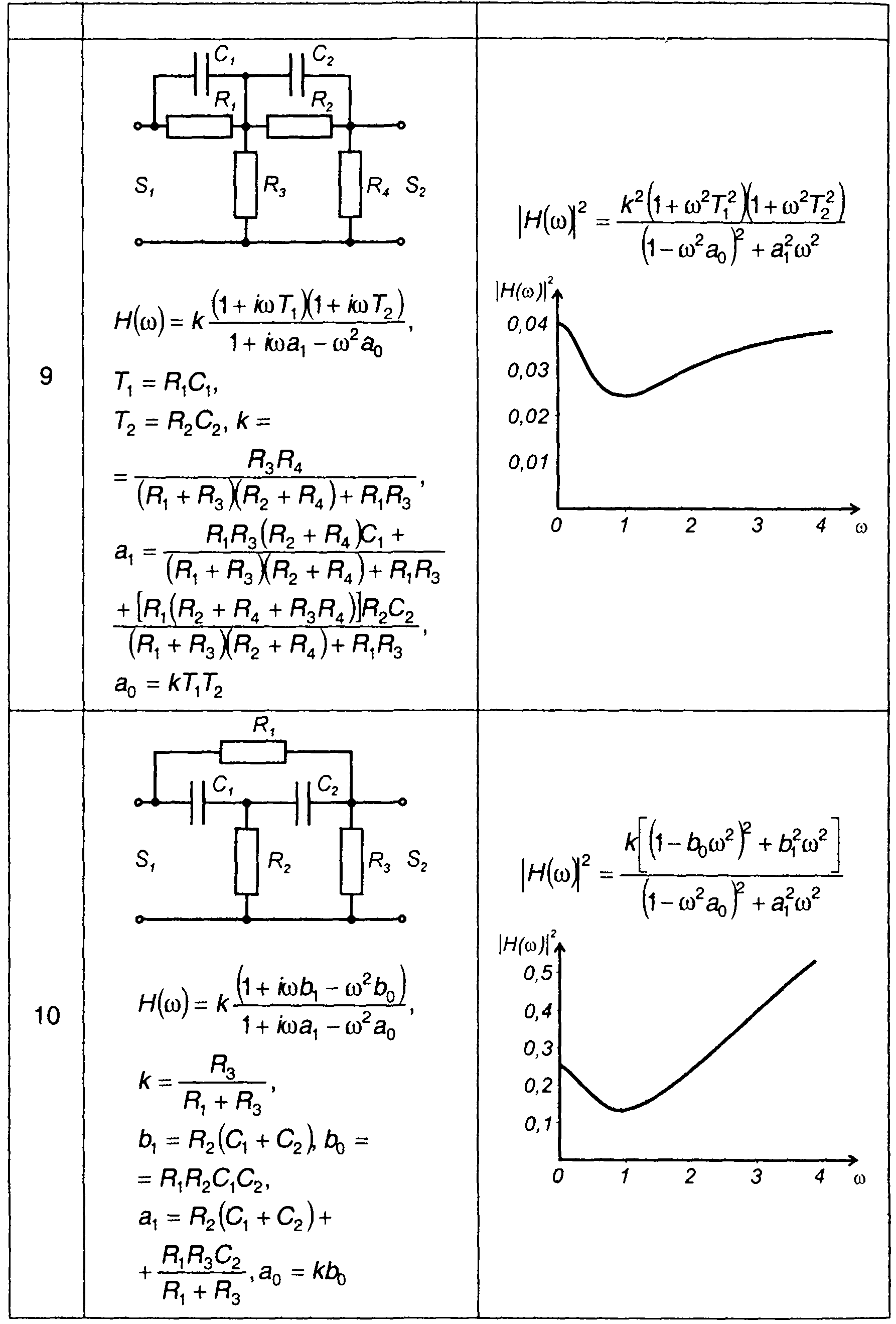
В качестве примеров в табл. 21.1 и 21.2 приведены наиболее простые, часто используемые в различных системах, цепи первого и второго порядков.

Таблица 21.1

Квадраты амплитудно-частотных характеристик цепей первого порядка

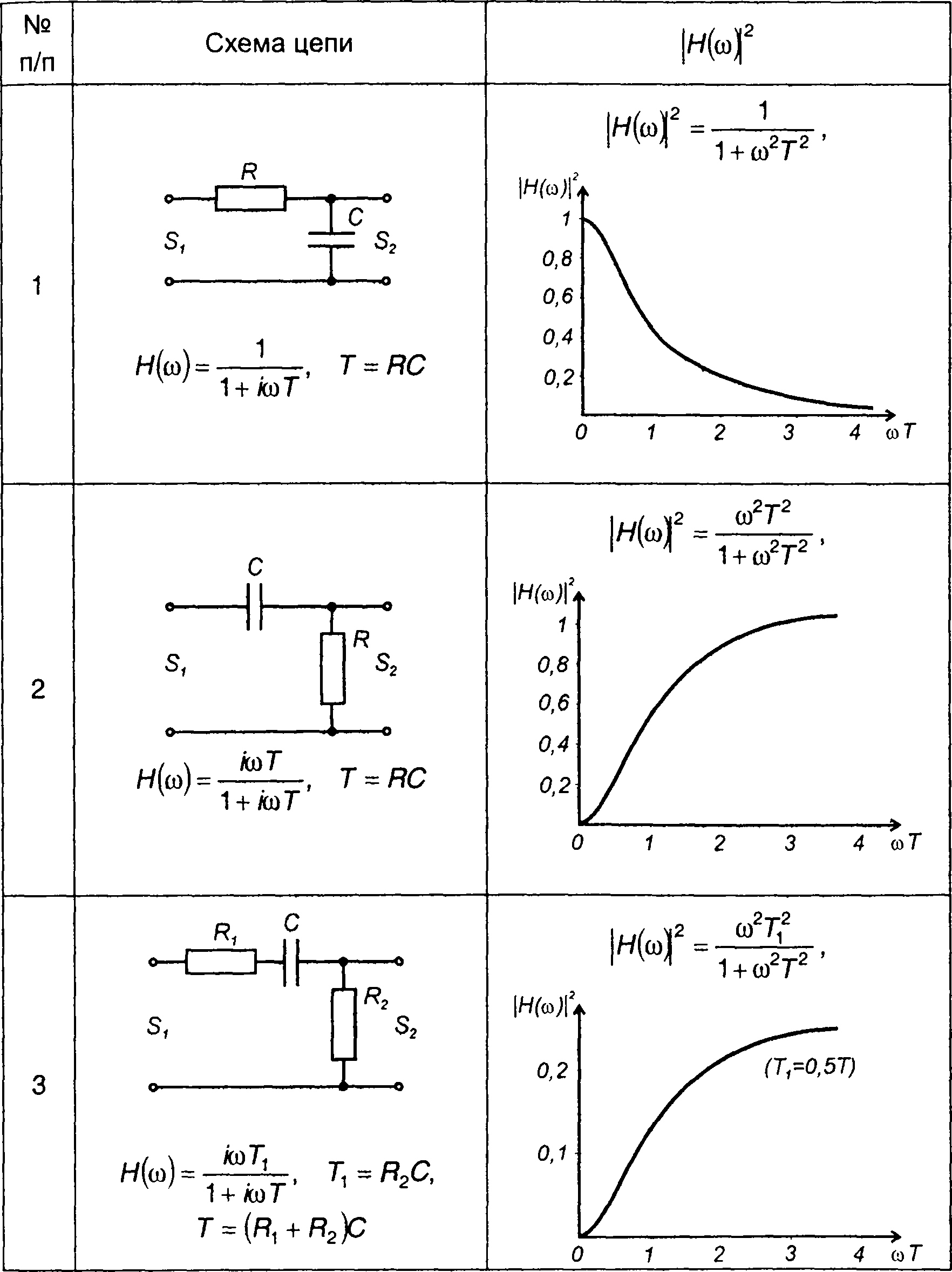
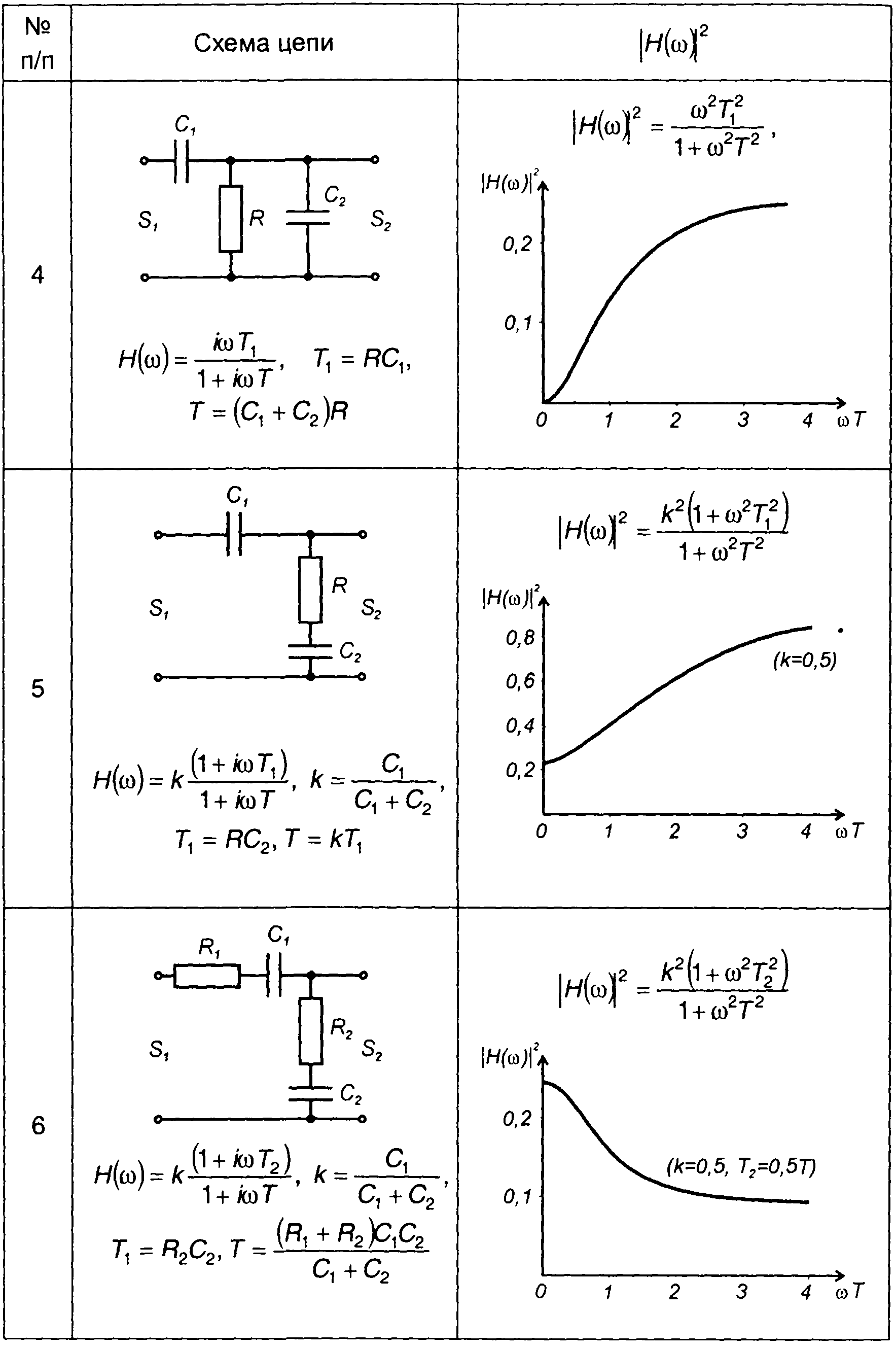
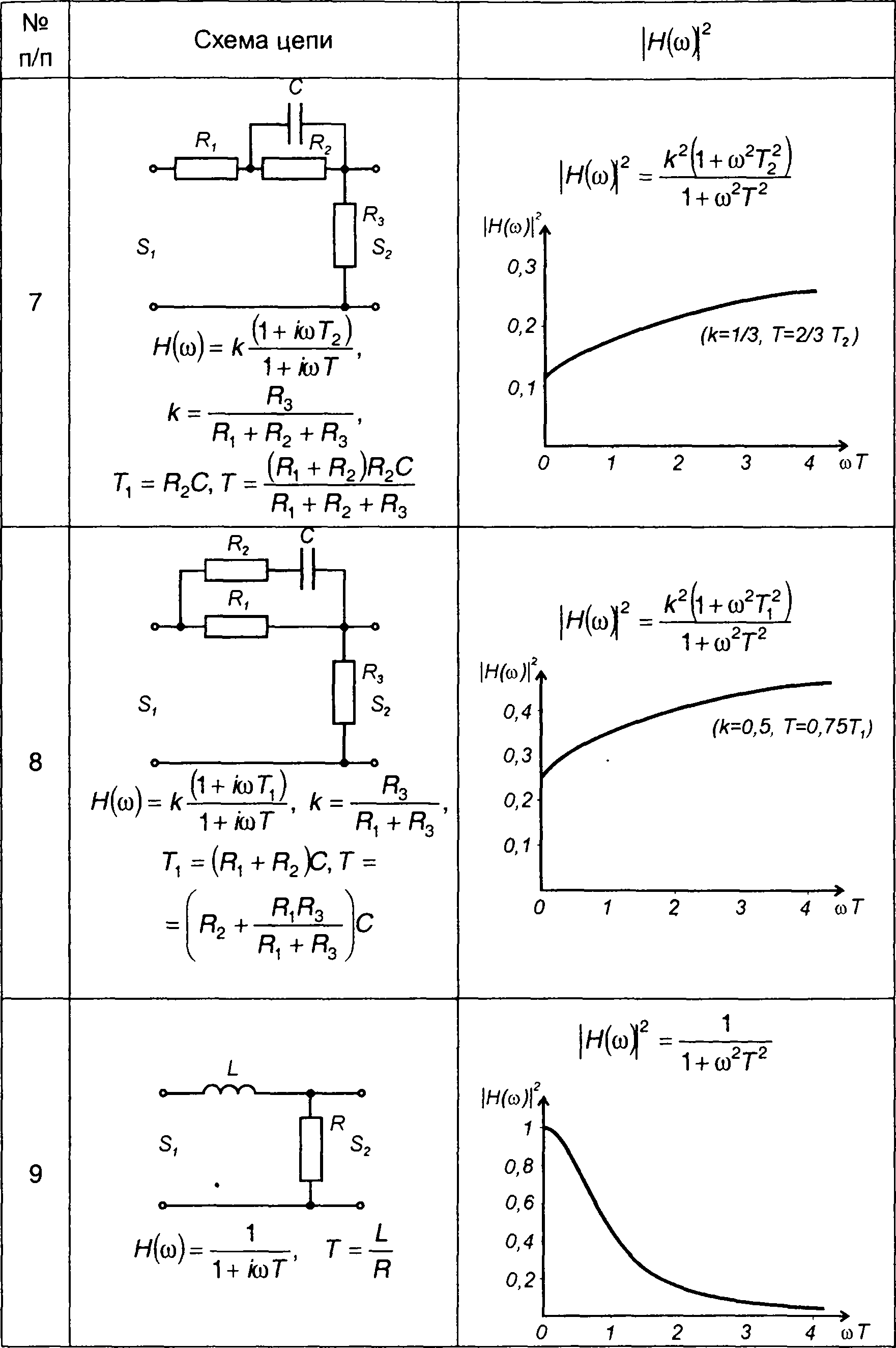
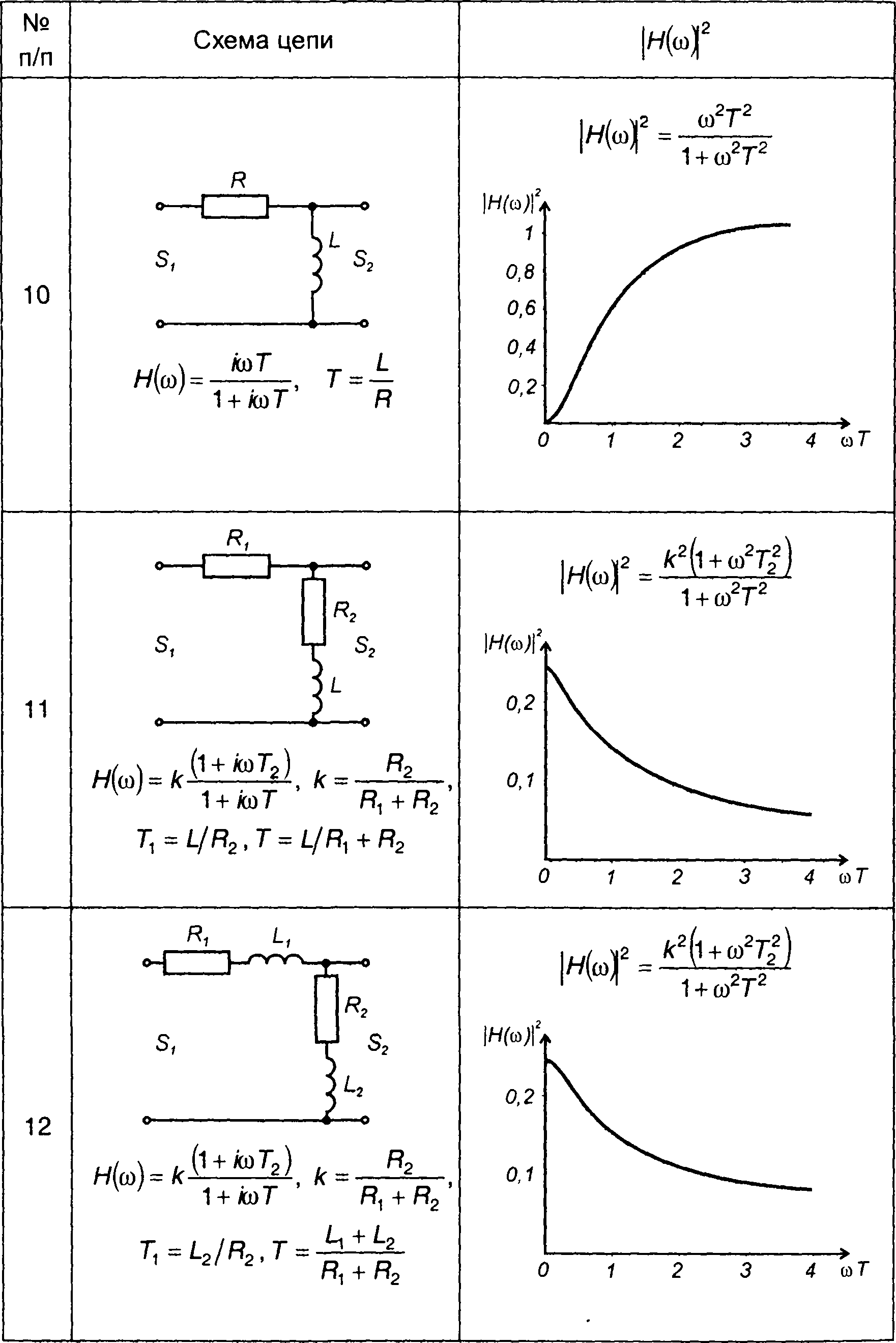
Таблица 21.2

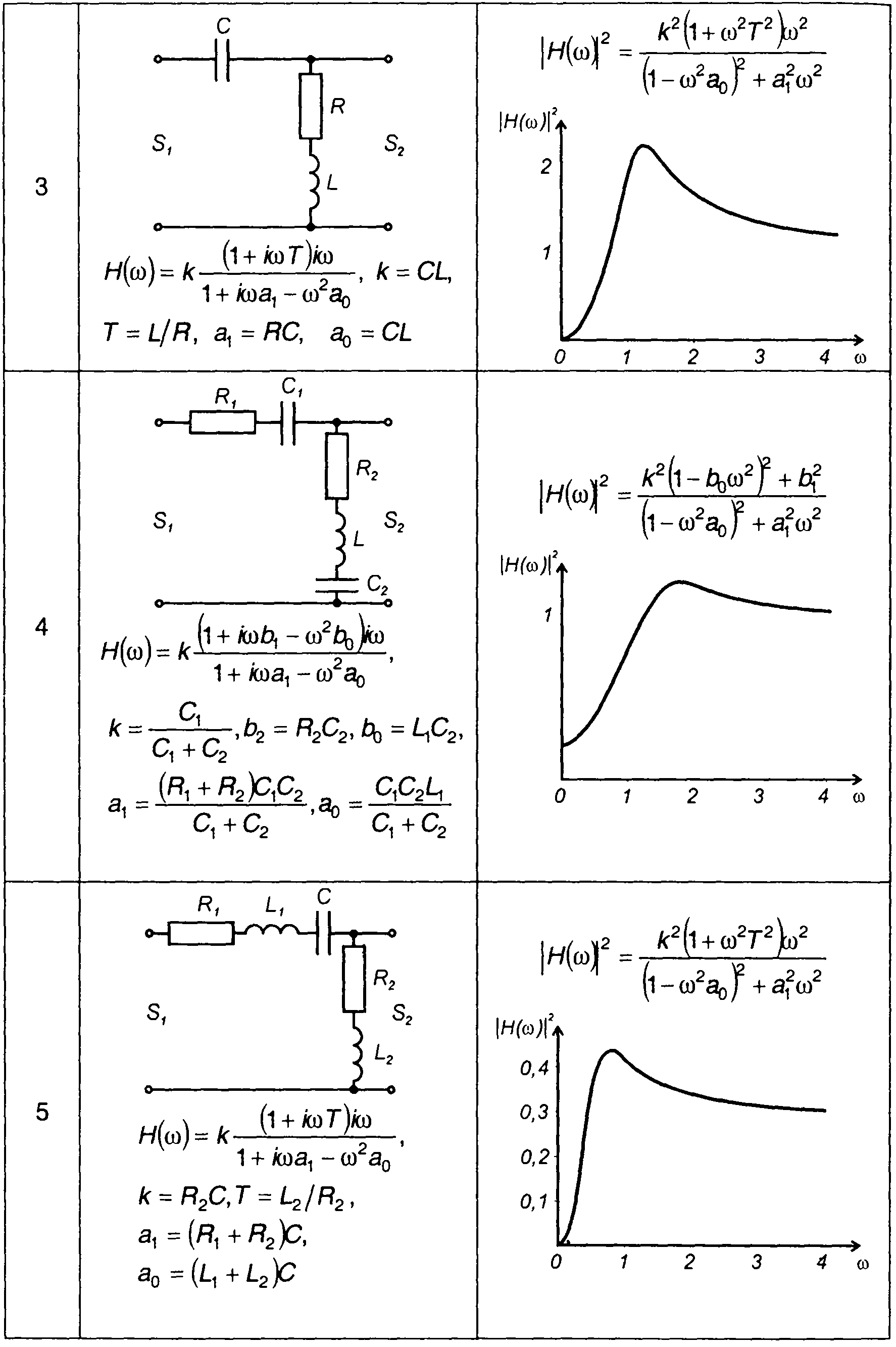
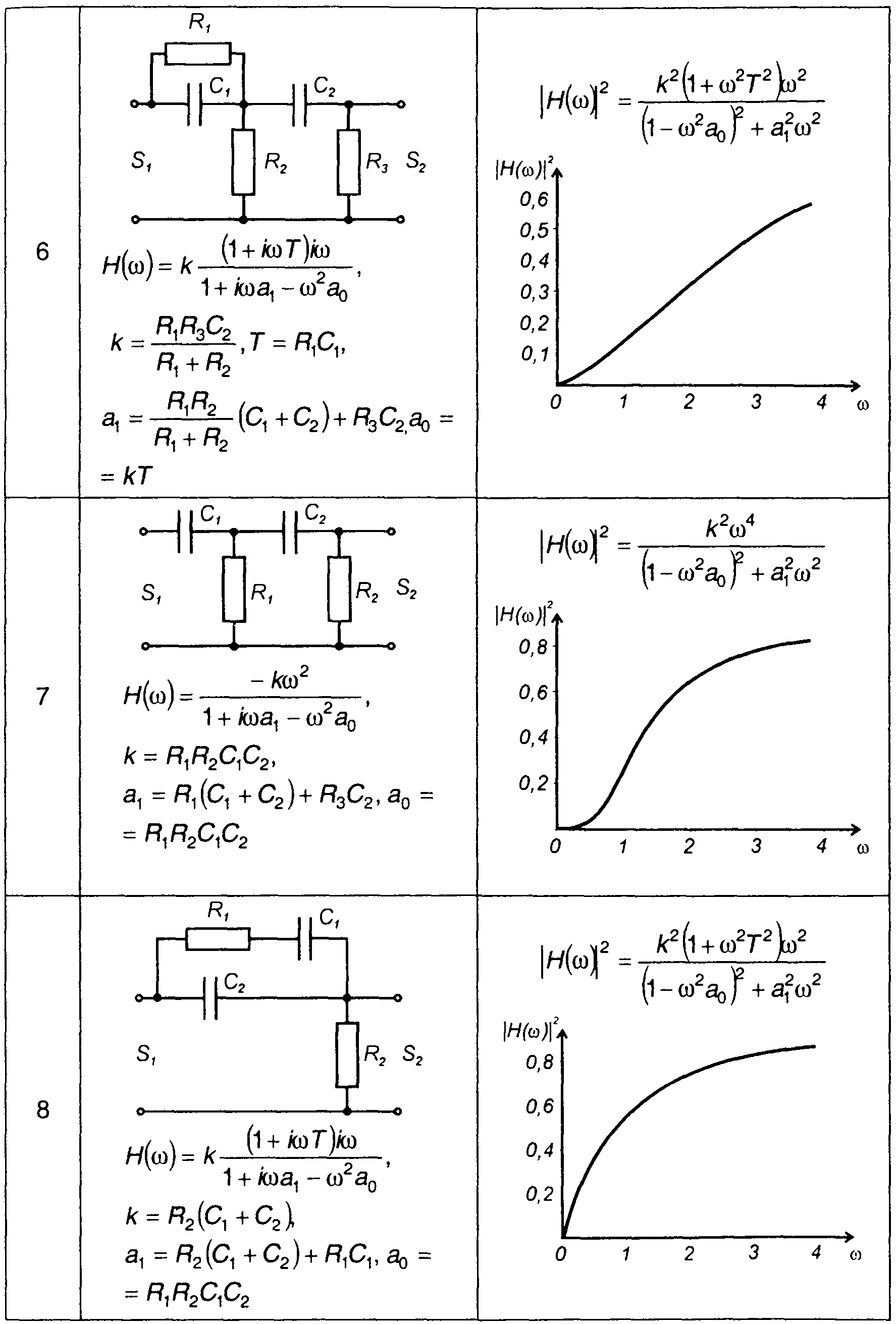
Квадраты амплитудно-частотных характеристик цепей второго порядка

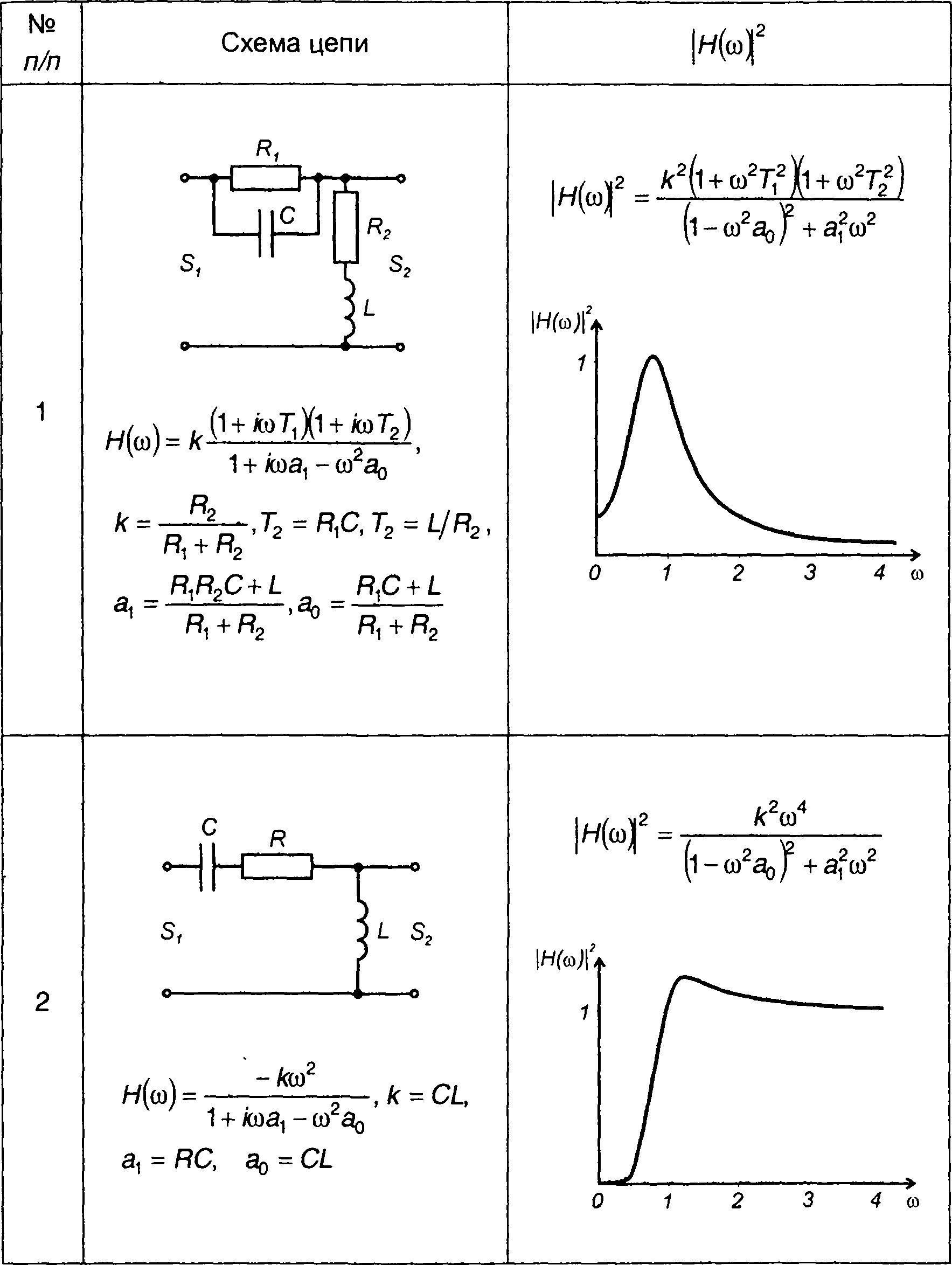
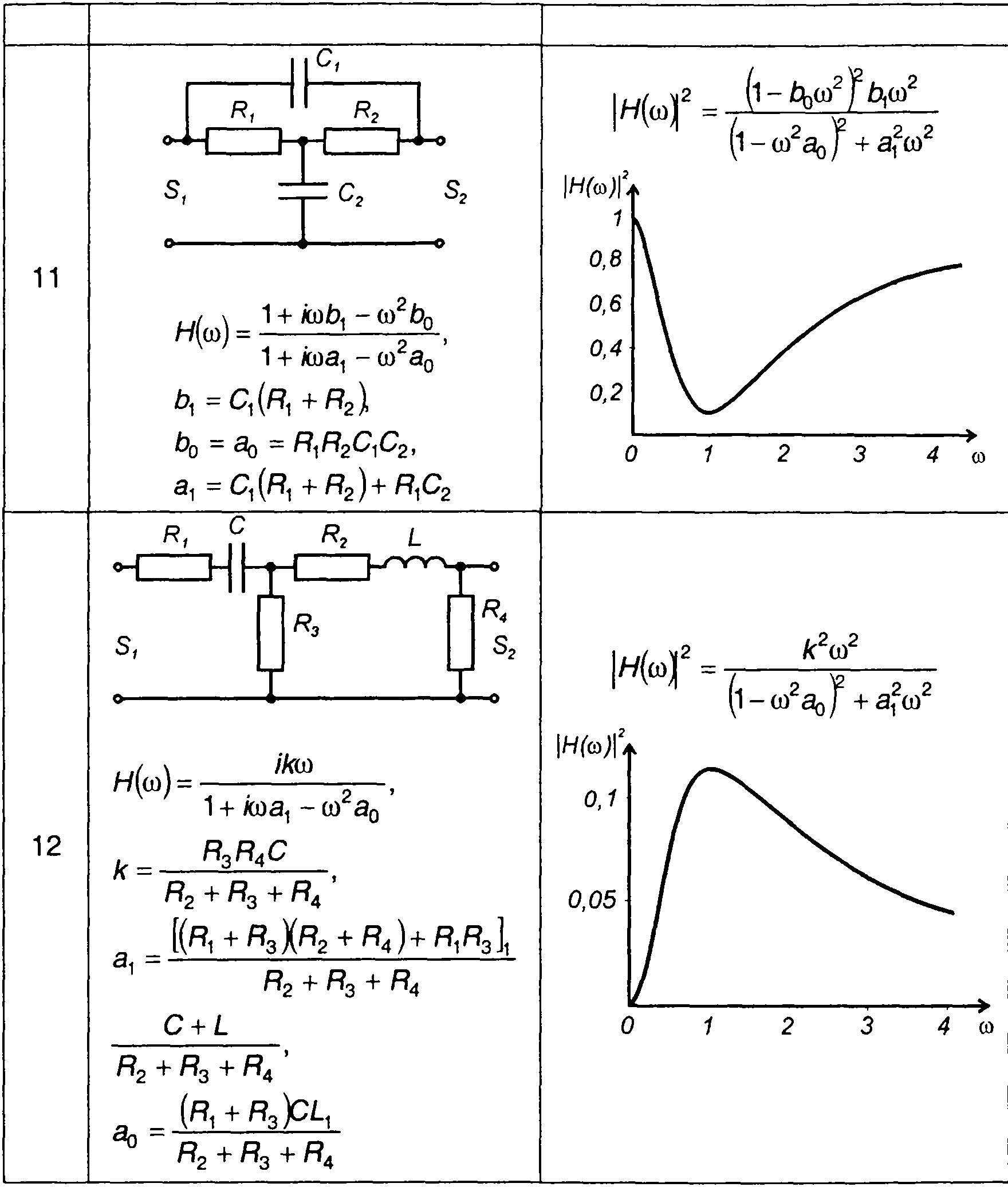
1. Для цепи, изображенной в табл. 21.1, п. 1,

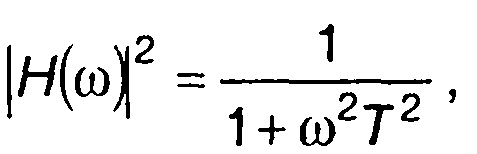
где Т - постоянная величина.

При

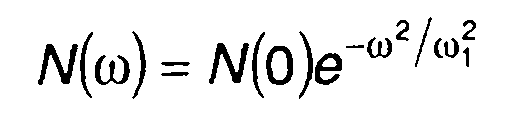
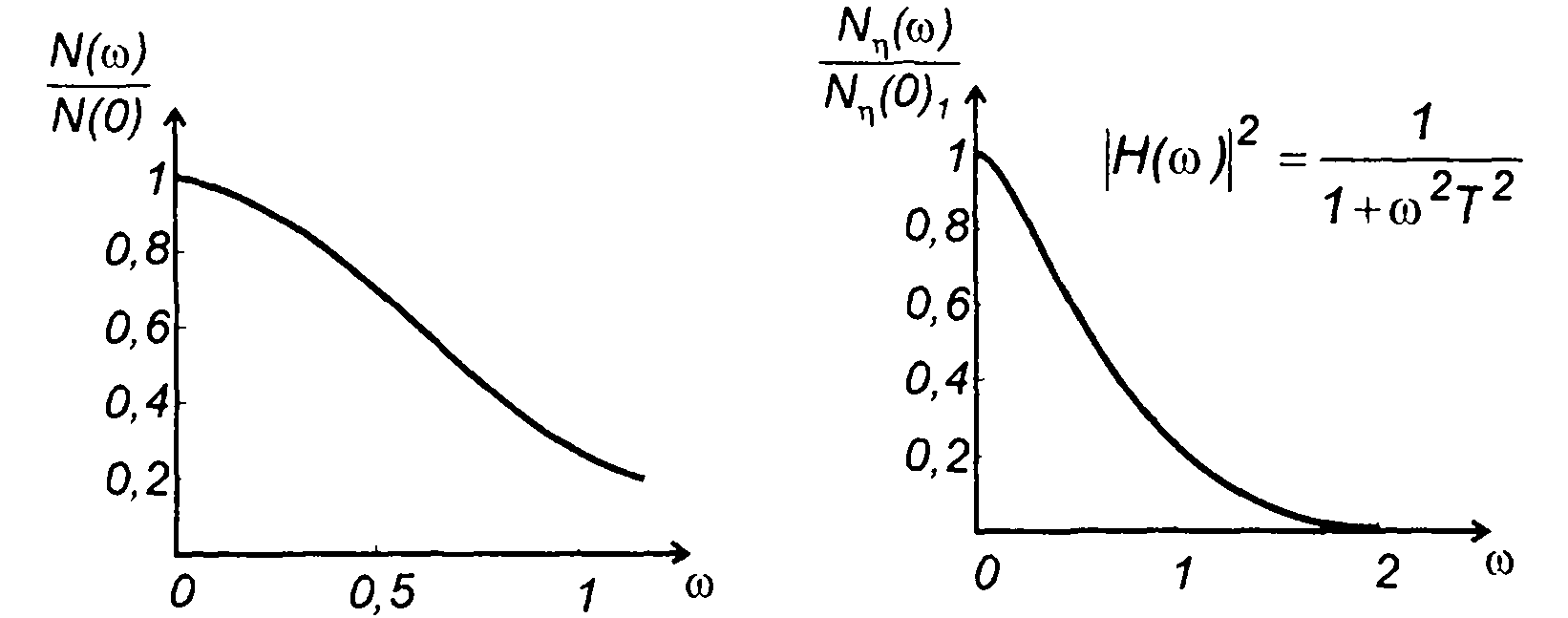
Рис. 21.1

на выходе цепи имеем (рис. 21.1)

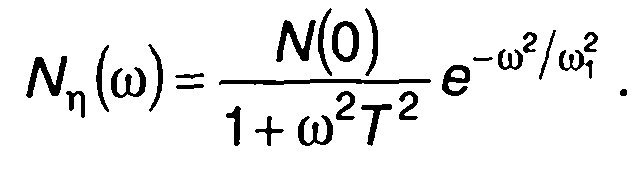
2. Для цепи второго порядка, изображенной в табл. 21.2, п.З,

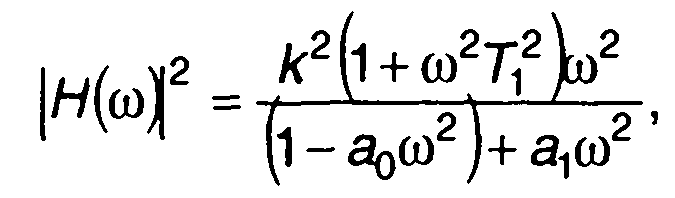
При

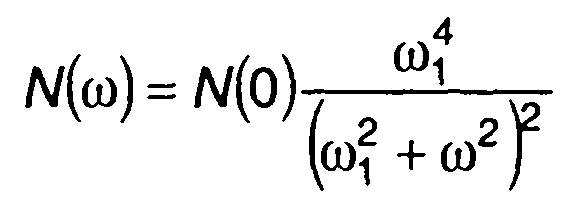
имеем (рис. 21.2)

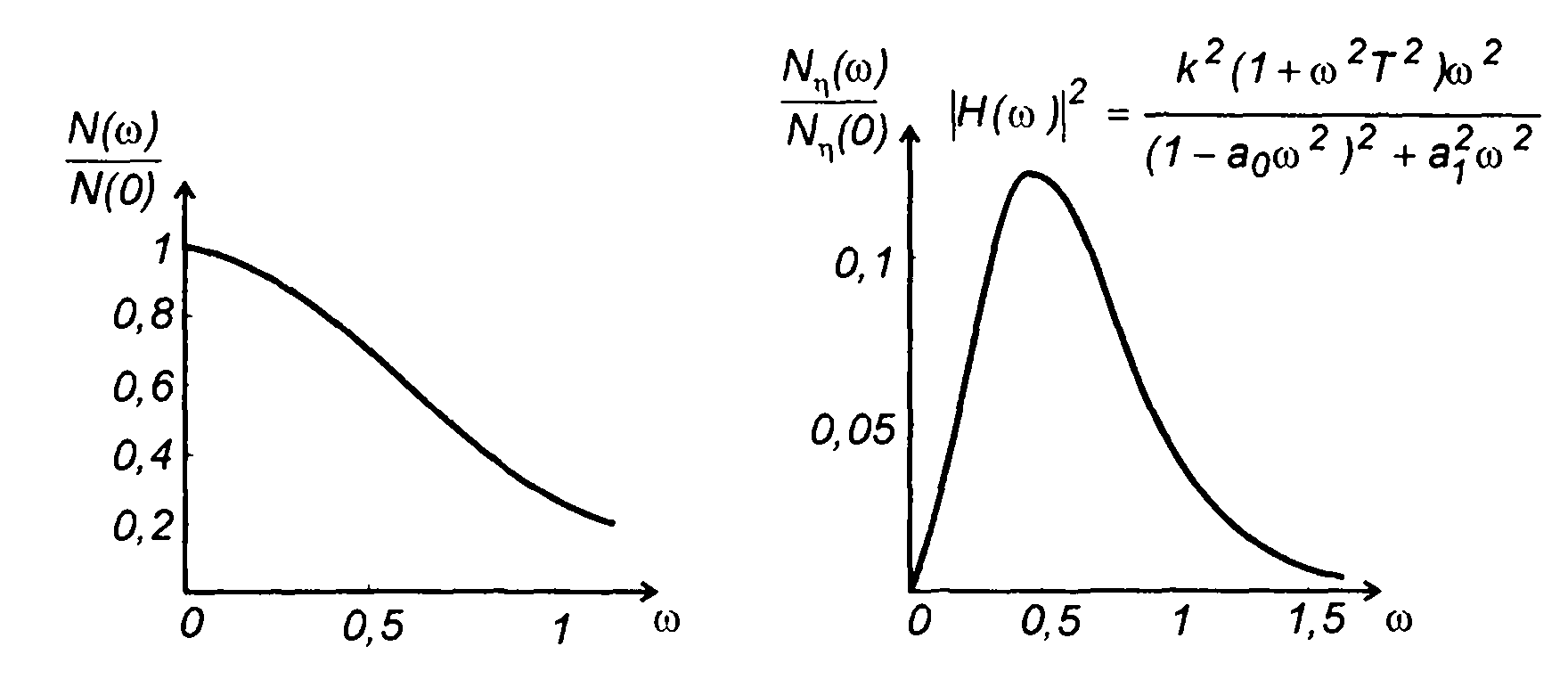
Рис.21.2

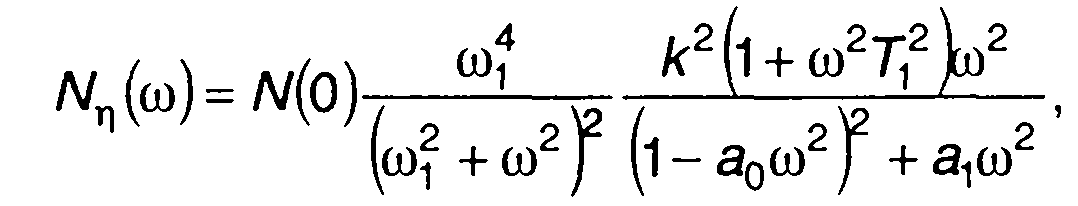
Преобразование Фурье позволяет перейти от спектра случайно­го процесса на выходе цепи к его корреляционной функции

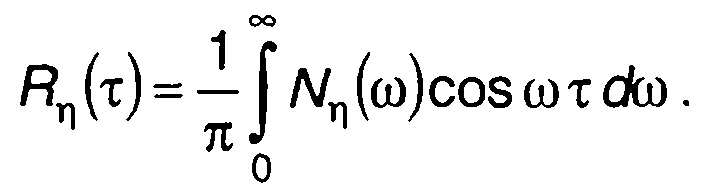
Определение корреляционной функции случайного процесса на выхода линейной цепи по его спектру часто бывает удобнее, чем непосредственное определение корреляционной функции во вре­менной области (в соответствии с выражениями, приведенными в предыдущем подразделе), даже в том случае, когда приходится прибегать к численным методам расчета. Иллюстрацией этого по­ложения служат и следующие примеры, связанные с анализом прохождения случайного процесса через RС-цепь с характеристи­ками:

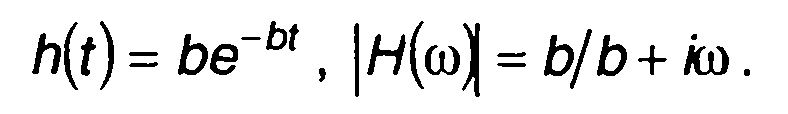
1. Корреляционная функция случайного процесса на входе цепи 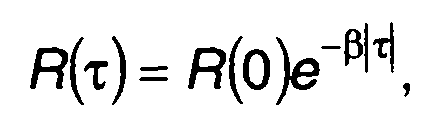спектральная плотность мощности случайного процесса на входе

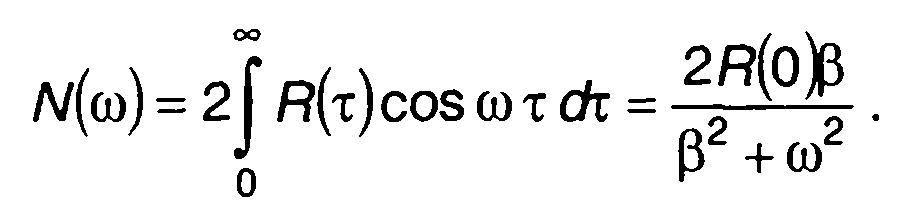
Спектральная плотность мощности случайного процесса на вы­ходе цепи

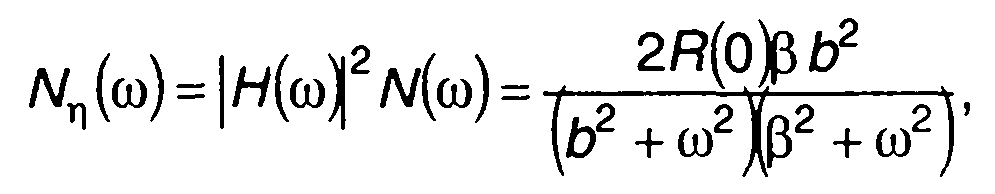
корреляционная функция случайного процесса на выходе (рис. 21.3)

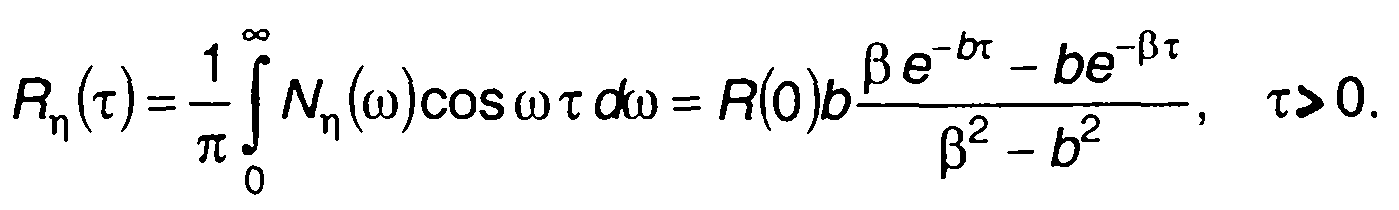
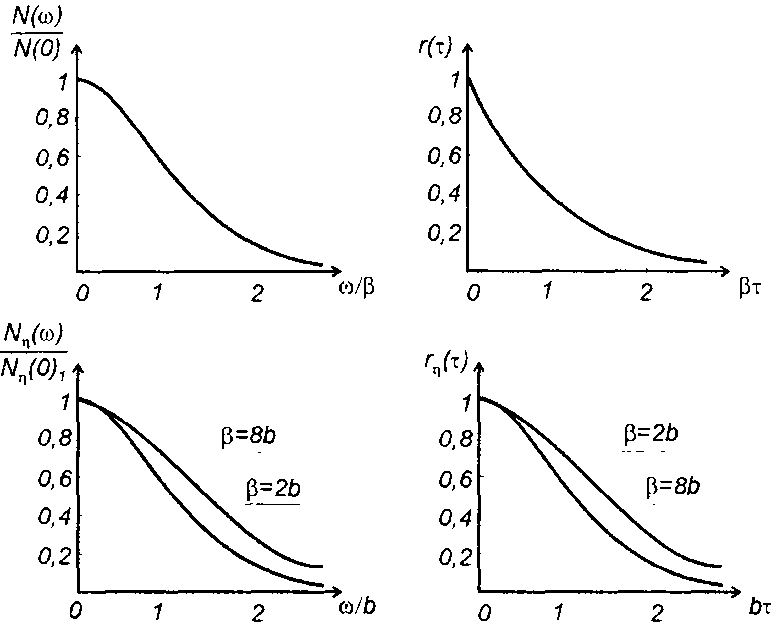
Рис.21.3

2. Корреляционная функция случайного процесса на входе цепи

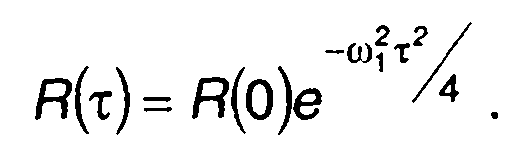
Спектральная плотность мощности случайного процесса на входе

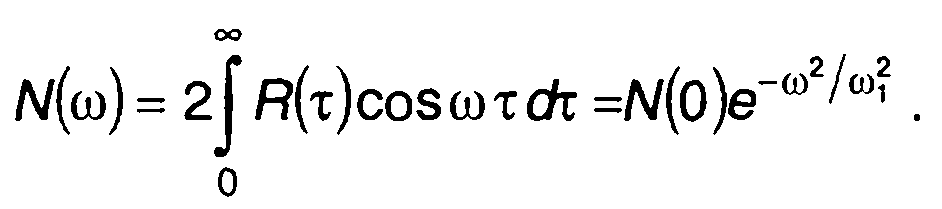
Спектральная плотность мощности случайного процесса на вы­ходе цепи

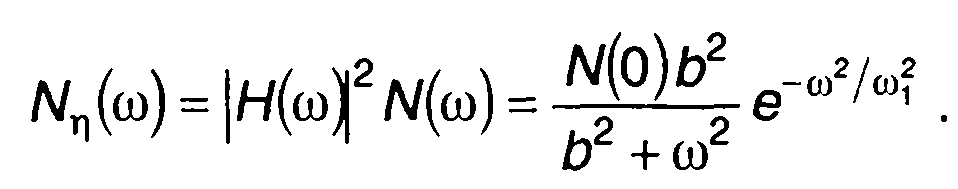
Корреляционная функция случайного процесса на выходе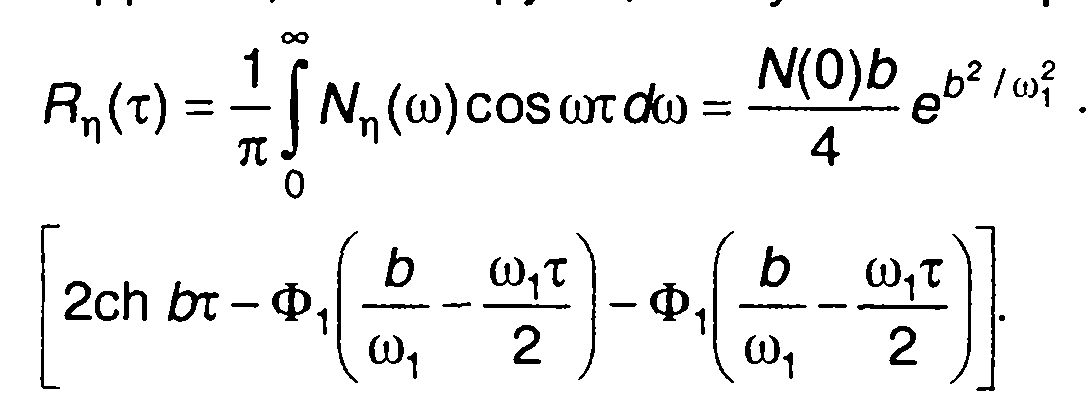

Если случайный процесс на входе представляет белый шум, то спектральная плотность мощности случайного процесса на выходе цепи определяется только частотной характеристикой цепи

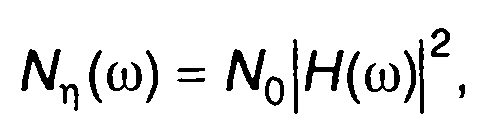(21.32)

где N₀ - спектральная плотность мощности белого шума.

При подаче на вход цепи белого шума корреляционная функция случайного процесса на выхода определяется выражением

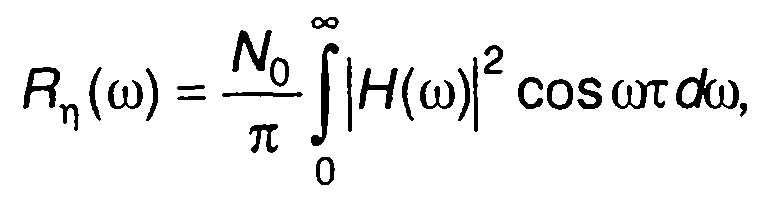(21.33)

т.е. определяется косинус-преобразованием Фурье квадрата моду­ля частотной характеристики цепи (с коэффициентом N₀). Ранее

эта корреляционная функция была определена с использованием импульсной характеристики.

При описании линейных цепей используется понятие полосы пропускания, или эквивалентной шумовой полосы. Эквивалентная шумовая полоса определяется как полоса пропускания цепи с иде­альной (прямоугольной) амплитудно-частотной характеристикой, соответствующей реальной цепи. Соответствие устанавливается по равенству среднего квадрата (дисперсии) случайного процесса на выходе цепи при подаче на вход белого шума. Для низкочастот­ной цепи эквивалентная шумовая полоса Д может быть определе­на из равенства (рис. 21.4,а)

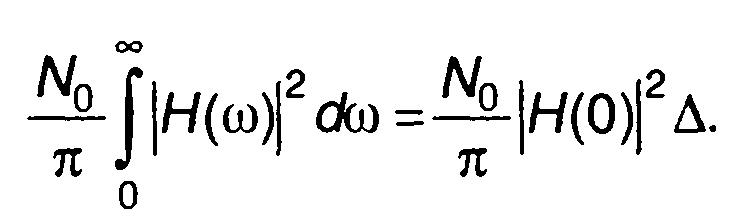
Таким образом, для ∆ получим следующее выражение

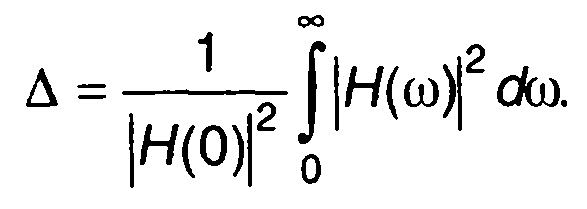(21.34)

В общем случае эквивалентная шумовая полоса определяется как (рис. 21.4,б)

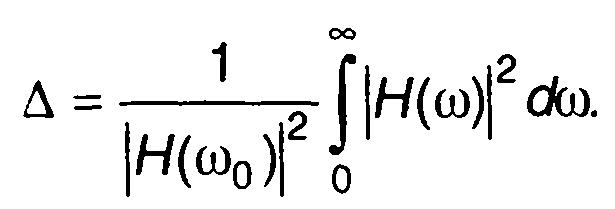(21.35)

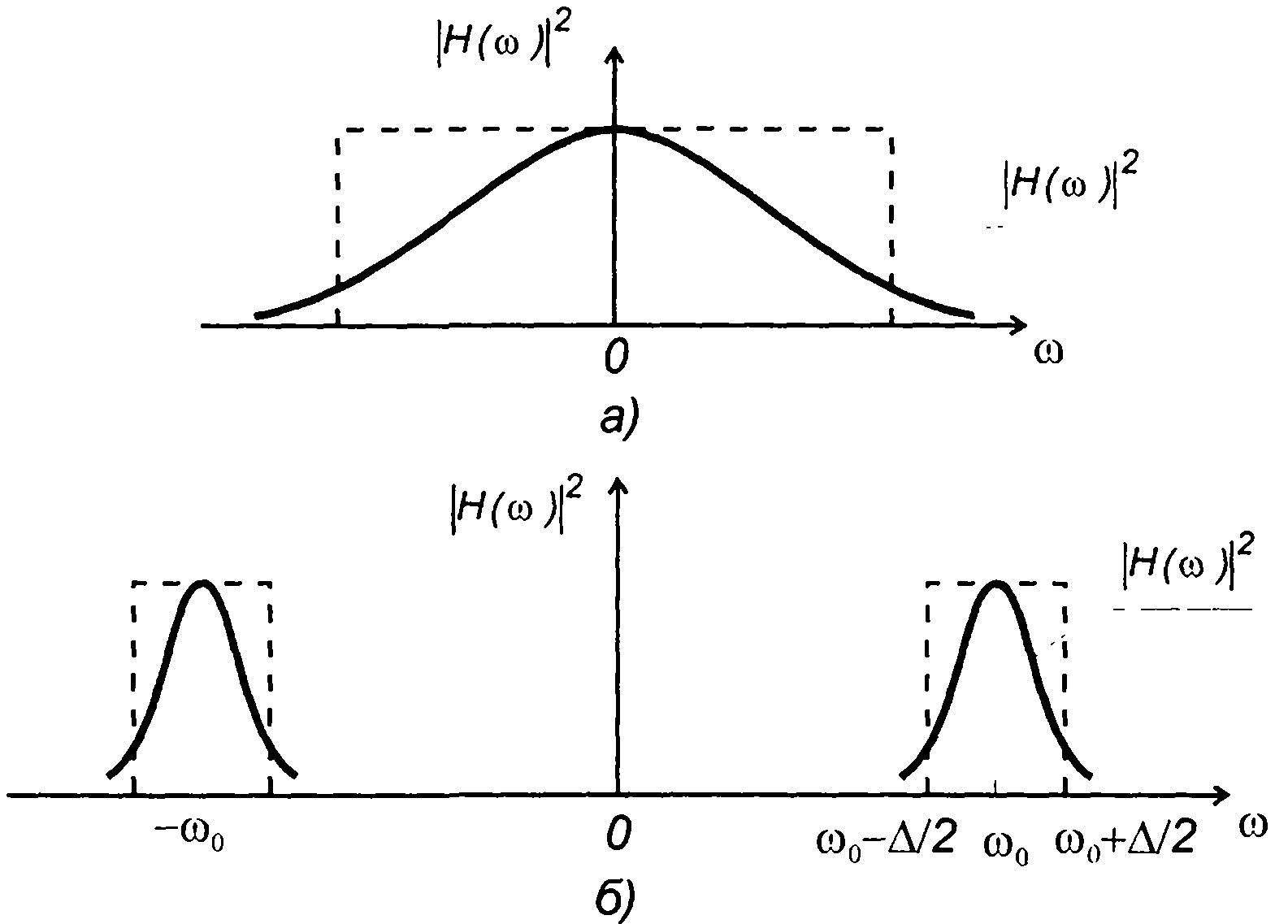
Рис.21.4

где ω₀ - характерная точка внутри полосы пропускания цепи, на­пример, получаемая из равенства:

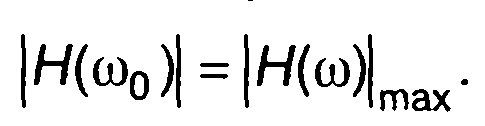
Из теоремы Парсеваля следует:

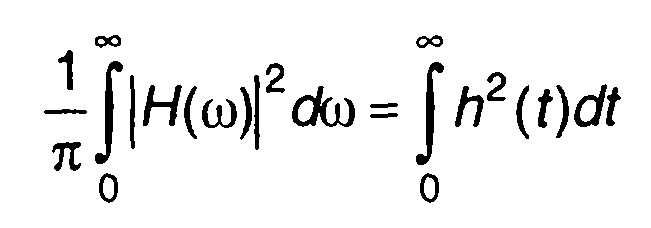(21.36)

Учитывая, что

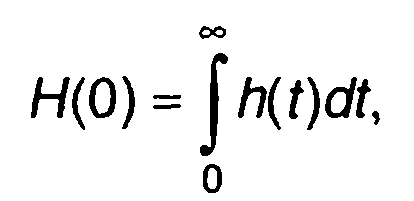
для эквивалентной шумовой полосы получим

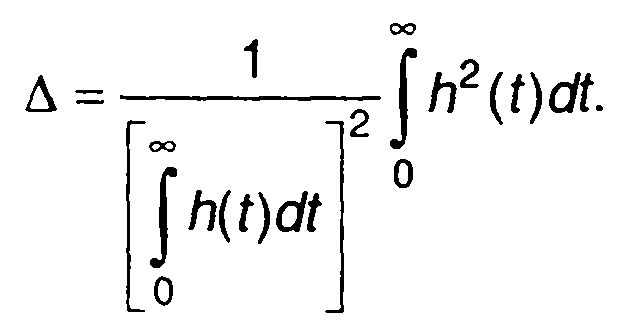(21.37)

Таким образом, (21.37) определяет эквивалентную шумовую полосу через импульсную характеристику цепи. Так для RС-цепи (табл. 21.1, п.1) с использованием частотной характеристики (вы­ражение (21.35)) получим

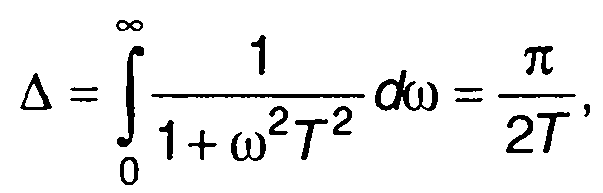
или с использованием импульсной характеристики (выражение (21.37))

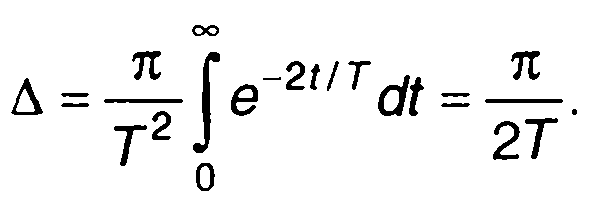
21.5. Оптимальные линейные цепи

Передача сигналов сопровождается шумами. Поэтому при приеме сигнала важно выбирать такие характеристики цепи, при которых влияние сопутствующих шумов будет минимальным. Цепь с такими характеристиками называют оптимальной цепью или оп­тимальным фильтром. Критерии оптимальности могут быть раз­личными, зависят в первую очередь от задач, решаемых при прие­ме сигнала. Если решается задача обнаружения сигнала на фоне шума, то в качестве критерия оптимальности целесообразно принять максимум отношения сигнал/шум на выходе цепи. При из­мерении параметров принимаемого сигнала в качестве критерия оптимальности принимается минимум среднего квадрата разности между сигналом на выходе цепи и его истинным значением. Воз­можны и другие критерии оптимальности. Ниже будут рассмотрены оптимальные линейные цепи, максимизирующие отношение сиг­нал/ шум.

Если на вход цепи поступает аддитивная смесь сигнал s₁(t) и шум ξ(t)^:

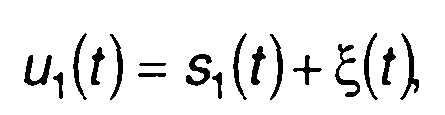(21.38)

то на выхода линейной цепи имеем

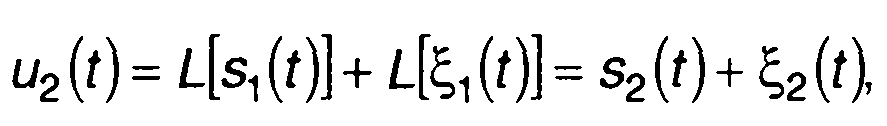(21.39)

где L - оператор линейной цепи.

В (21.57) s₂(t)=L[s₁(t)] представляет сигнал, a ξ₂(t)⁼L[ξ₁(t)] - шум на выходе цепи. Требуется определить характеристики ли­нейной цепи, при которых отношение сигнал/шум на выходе цепи в заданный момент времени