ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 23 страница

где f_{ξ 2}(x₁, х₂) - двумерная ПРВ ξ(t) и ξ(t -t₃).

При нормальном распределении случайного процесса ξ(t) раз­ность ξ(t) - ξ(t - t₃). имеет также нормальное распределение с дис­персией

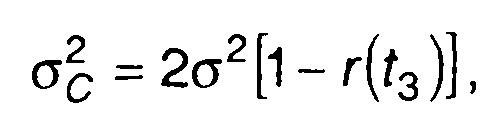(20.40)

где R(т) σ² = R(0) г(τ)=R(т)/R(0) - корреляционная функция, дис­персия и нормированная корреляционная функция ξ(t).

Таким образом, для случайной величины (20.38) при нормаль­ном распределении ξ(t) получим

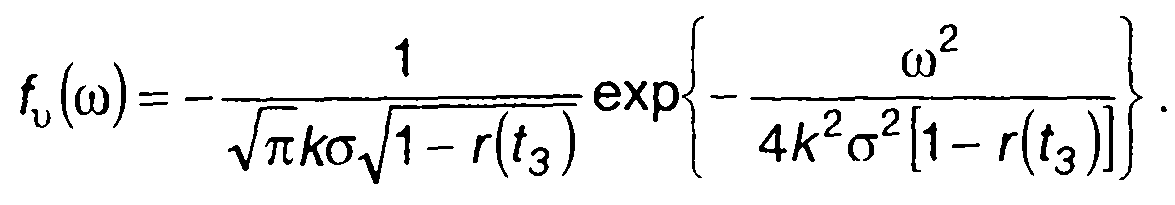(20.41)

Средняя частота случайного процесса на выходе смесителя

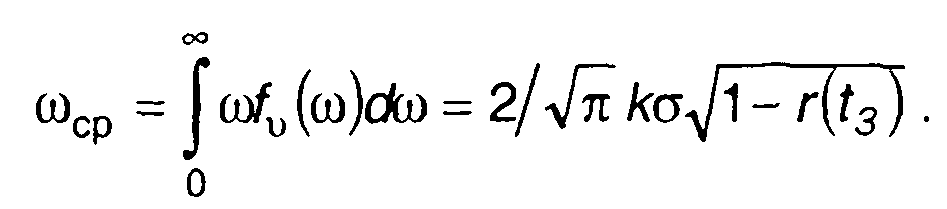(20.42)

Как следует из (20.42), для заданного значения времени за­держки средняя частота на выходе смесителя зависит от значения корреляционной функции модулирующего случайного процесса.

Длительность положительных и отрицательных выбросов слу­чайного процесса на выходе смесителя связана с частотой соот­ношением δ = π/v. Из (20.33) и (20.41) получим (рис. 20.8,а)

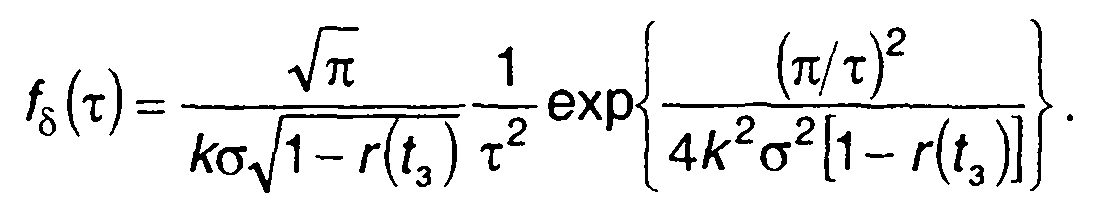(20.43)

ФРВ длительности выбросов равна (рис. 20.8,б)

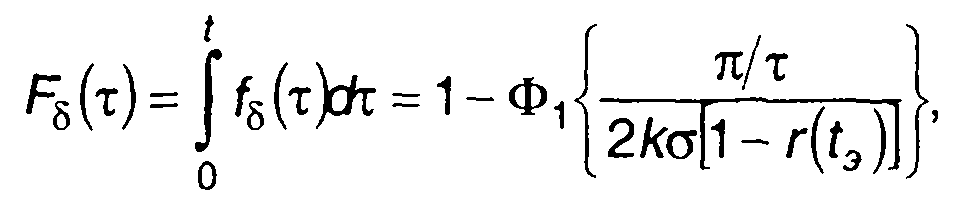(20.44)

где

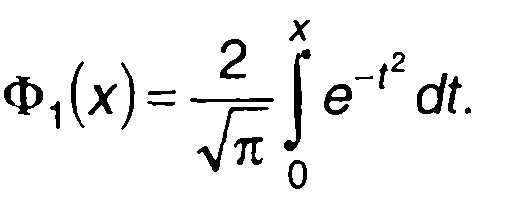
20.2.2. Распределение длительности выбросов случайного процесса, общая постановка задачи

Центрированный случайный процесс представим в виде

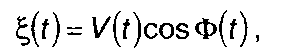(20.45)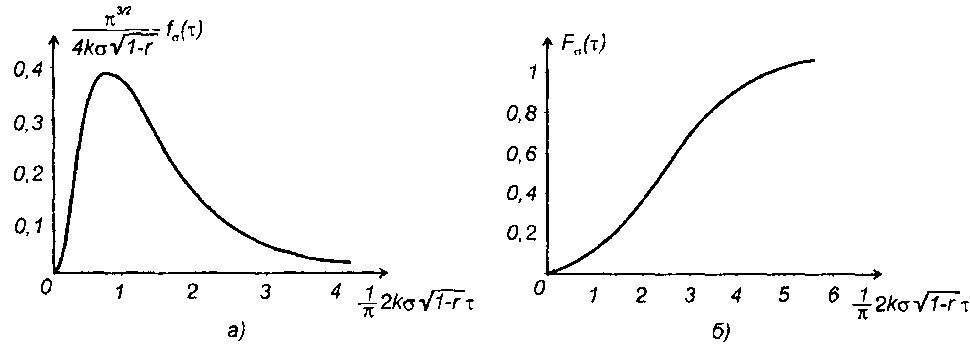

Рис.20.8

не накладывая на него условия узкополосности. Записанное выра­жение аналогично тому, какое описывает случайный процесс с уг­ловой модуляцией на выходе смесителя (п. 20.2.1). Функции V(t) и Ф(t) являются случайными функциями времени. Каждой реализа­ции ξ(t) соответствуют реализации амплитуды V(t) и частоты v(t). Двумерную ПРВ случайных величин V(t) и v(t) обозначим f_2Vv (и,ω). Дисперсия

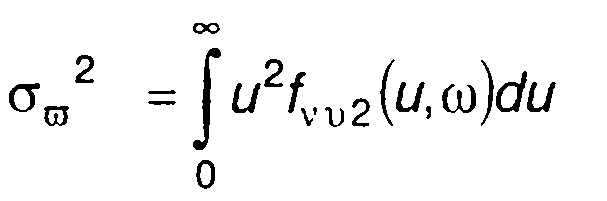(20.46)

характеризует распределение мощности случайного процесса по частоте. Такое же распределение дает и спектральная плотность мощности случайного процесса 1/πN(ω). Однако определить f_u(ω), используя (20.46), в общем случае не удается вследствие неопре­деленности задания V(t) и u(t). Задача упрощается для случайно­го процесса ri(f) с независимыми V(t) и u(t). Для него

Таким образом, для случайного процесса η(t) имеем

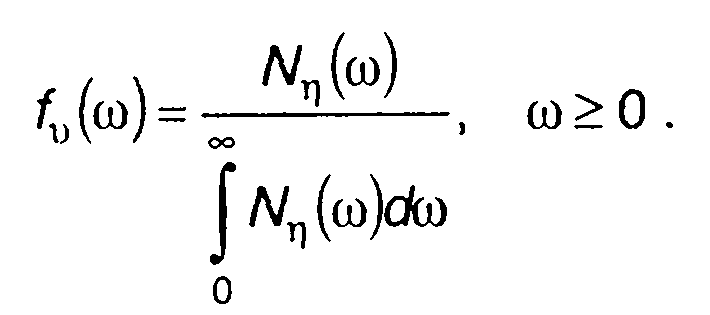(20.47)

Такая зависимость справедлива для клиппированного случайно­го процесса - случайного процесса на выходе идеального ограни­чителя

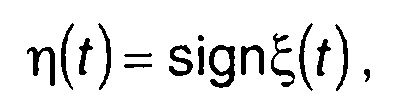(20.48)

где ξ(t) - случайный процесс на входе.

Спектральную плотность мощности случайного процесса η(t) удобнее определить через корреляционную функцию R_η(ω)

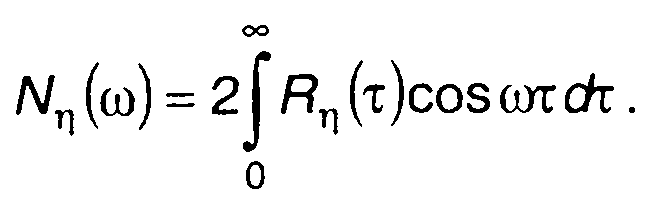(20.49)

Методы определения R_η(т) гауссовского процесса изложены в разд. 22. Для гауссовского процесса имеем

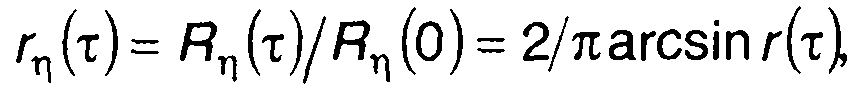(20.50)

где r(τ) - нормированная корреляционная функция исходного слу­чайного процесса ξ(t).

Таким образом, зная корреляционную функцию гауссовского процесса R(т) или соответствующий спектр N(ω), можно получить ПРВ или ФРВ частоты.

Функция распределения вероятностей частоты случайного про­цесса определяется выражением

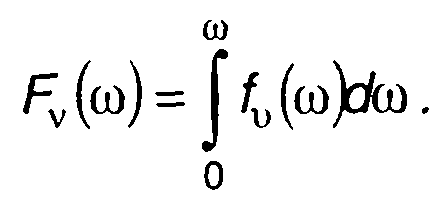(20.51)

В качестве примера рассмотрим гауссовский процесс, имеющий характеристики:

корреляционная функция (рис. 20.9,а)

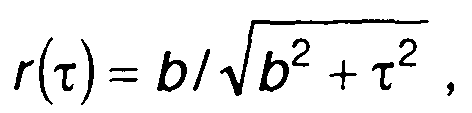
спектральная плотность мощности (рис. 20.9,а)

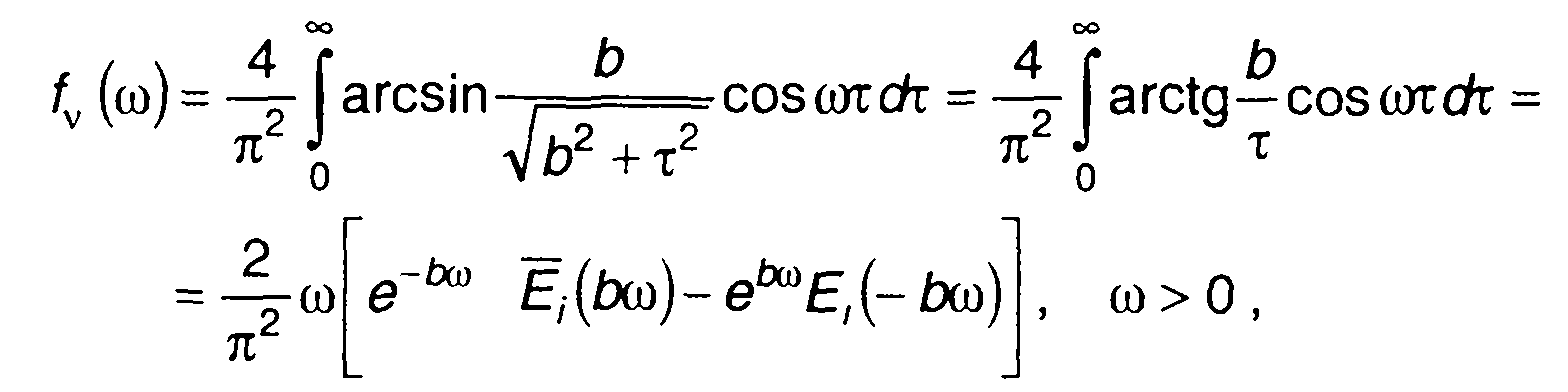
где Е(х) - интегральная показательная функция.

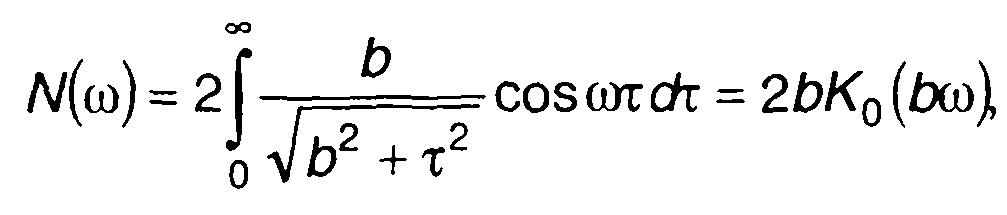
где Ко(х) - модифицированная функция Бесселя.

Плотность распределения вероятностей частоты случайного процесса описывается выражением

График ПРВ частоты изображен на рис. 20.9,б.

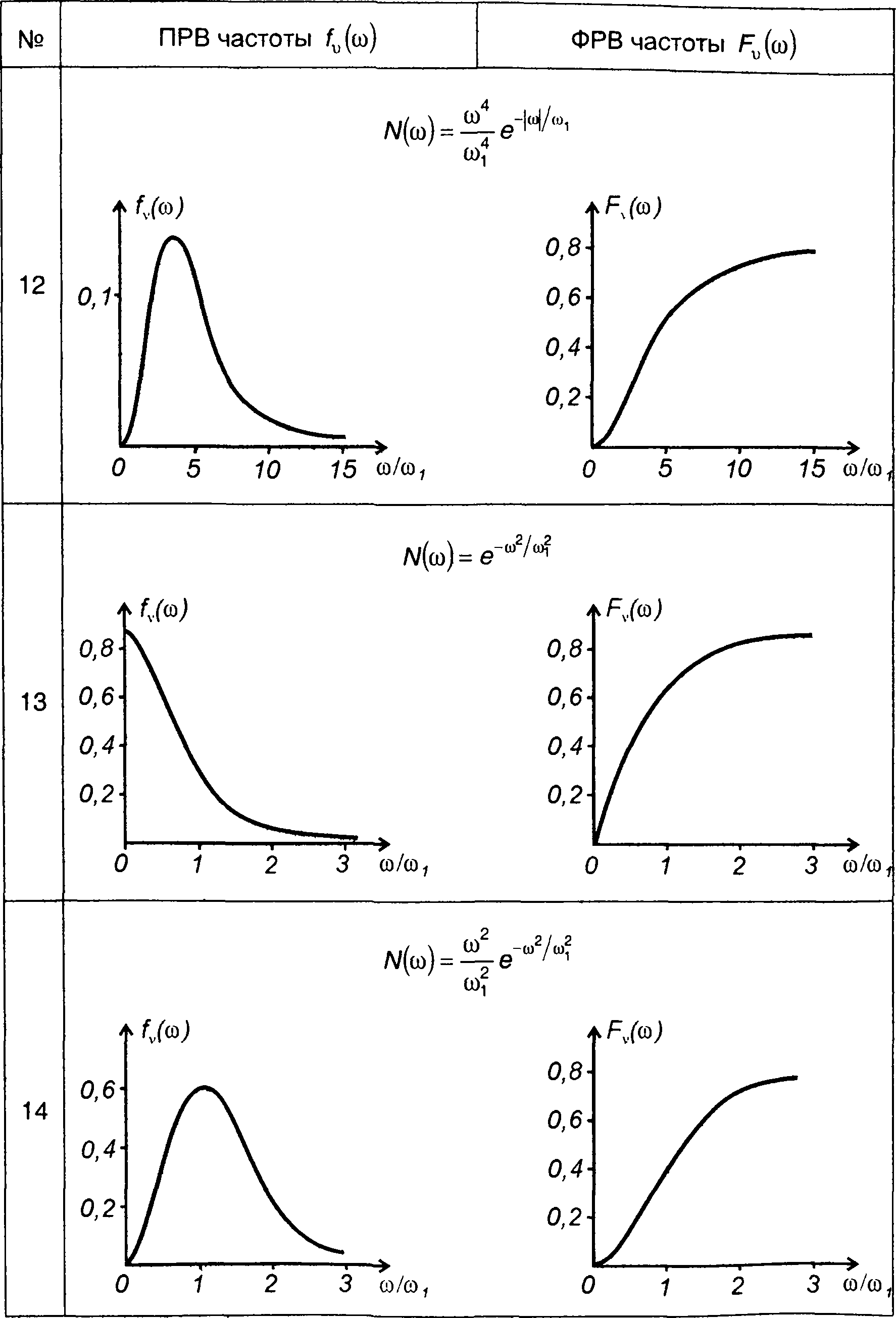
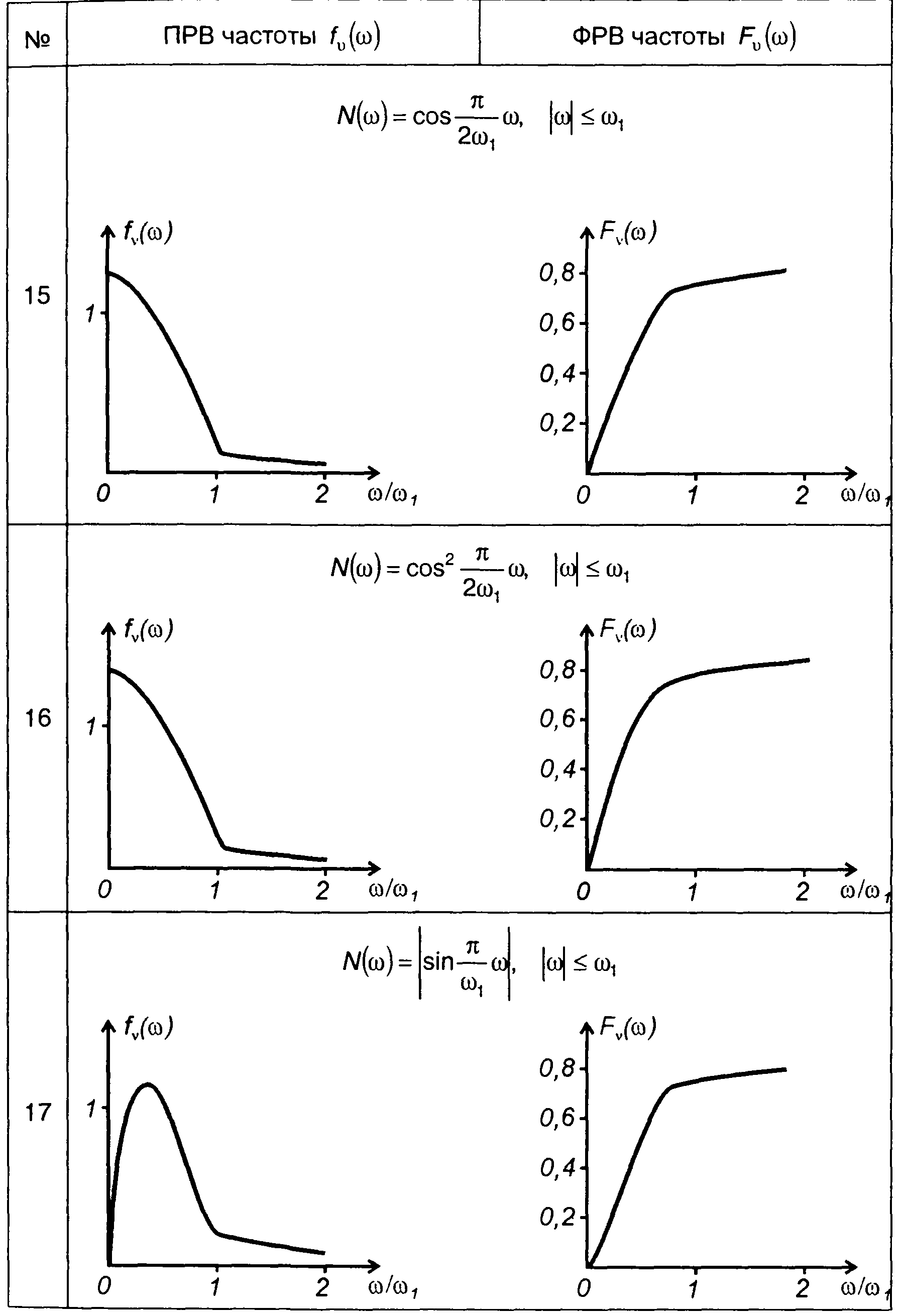
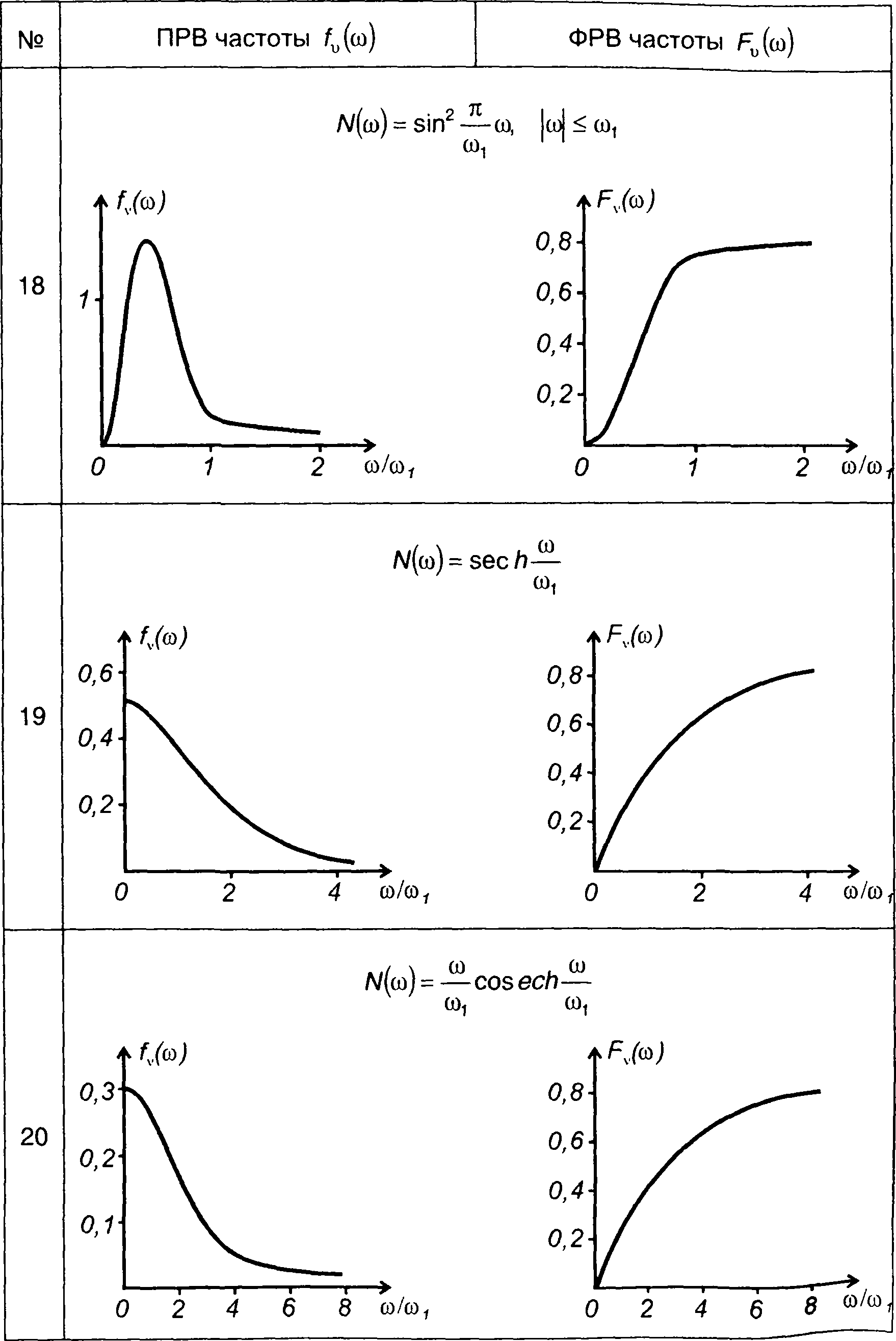
На рис. 20.10 - 20.12 изображены графики ПРВ частоты гауссовских процессов, характеристики которых приведены в табл. 18.1.

На рис. 20.10 для характеристик - табл. 18.1, п.4

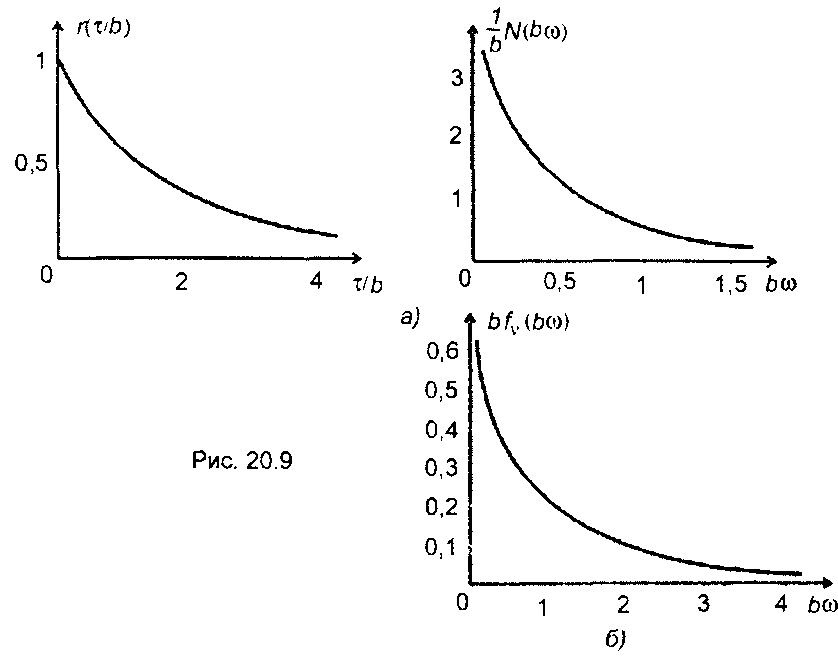
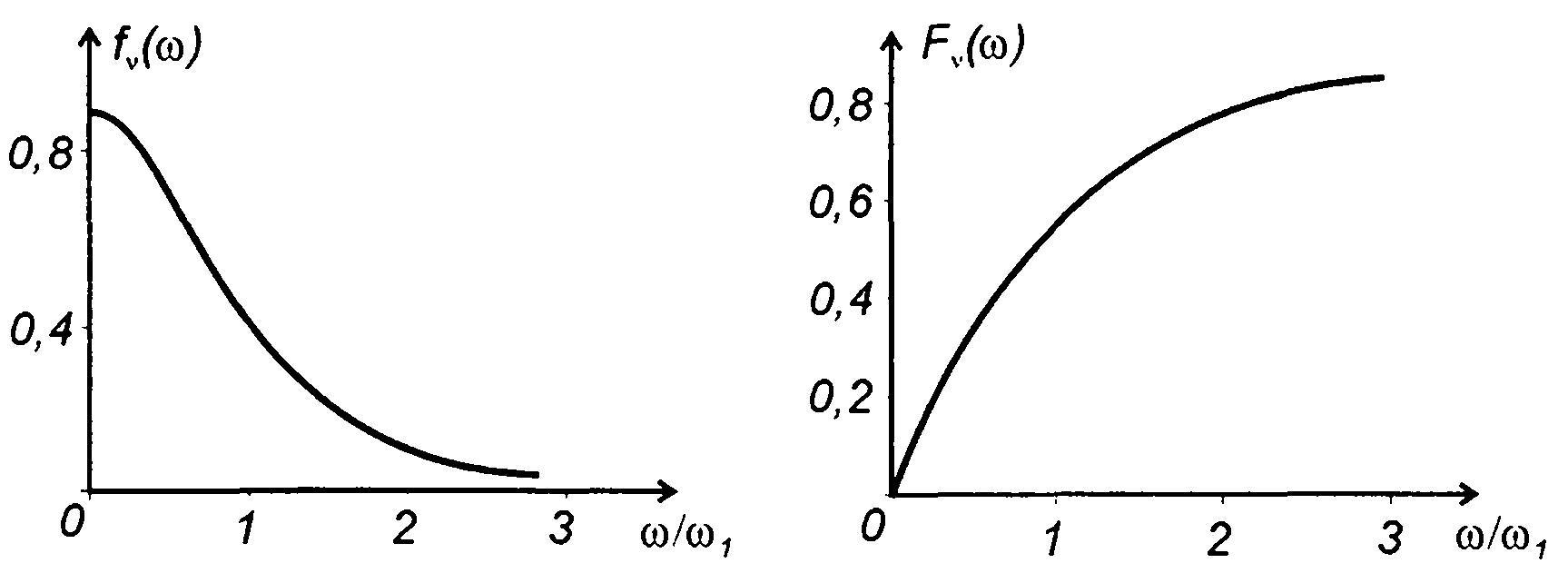
Рис. 20.10

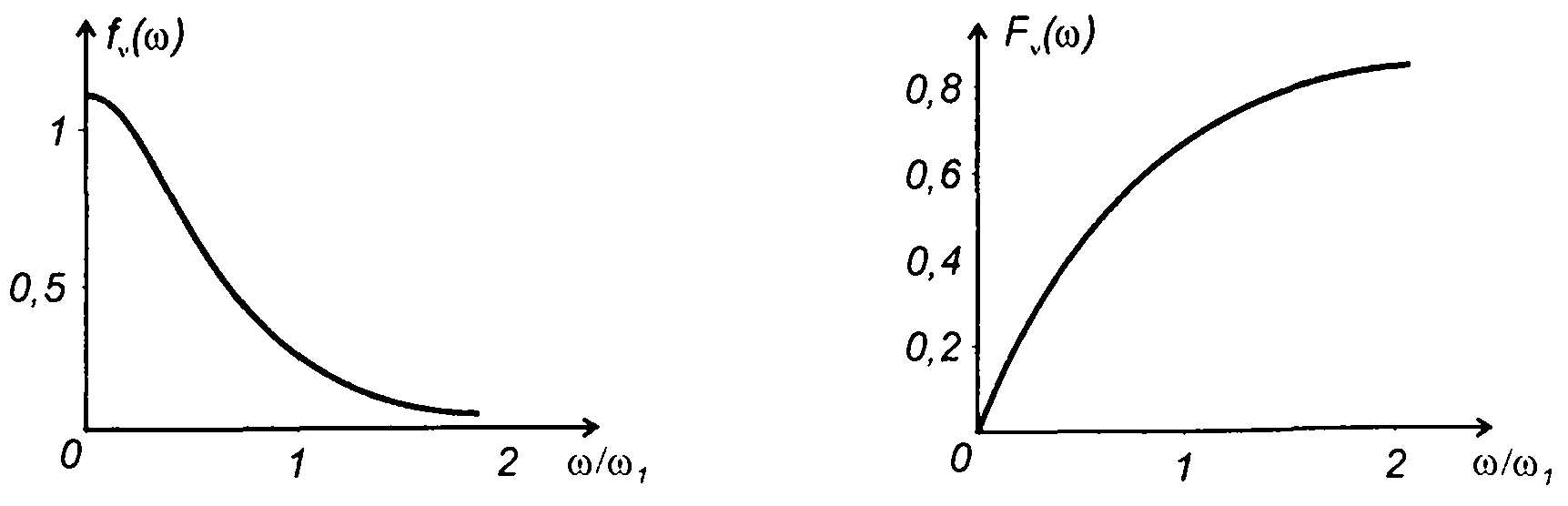
Рис. 20.11

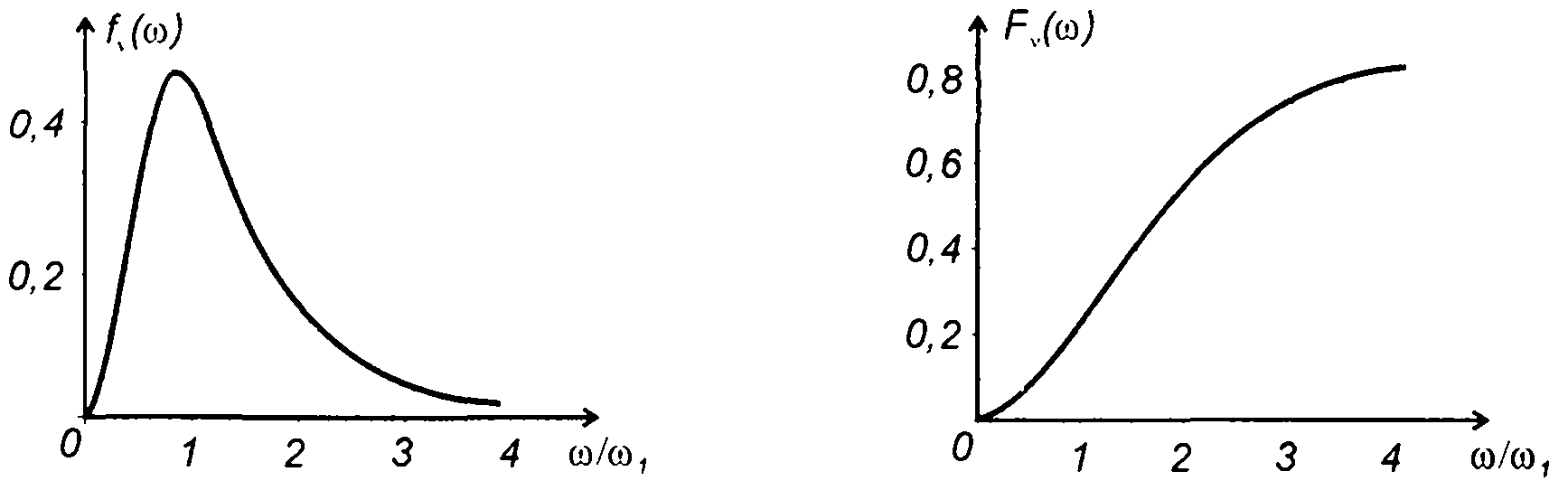
Рис. 20.12

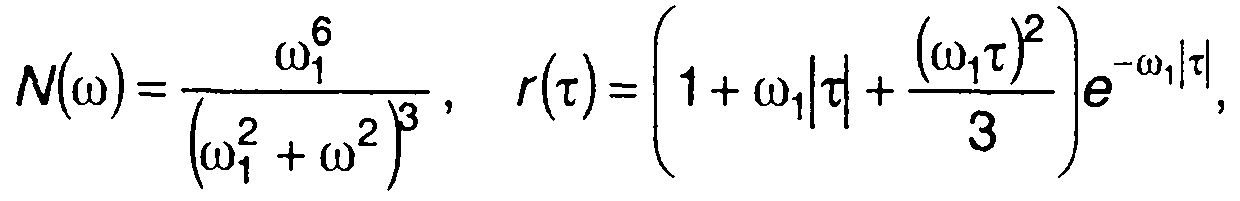
на рис. 20.11 - для характеристик-табл. 18.1, п.5

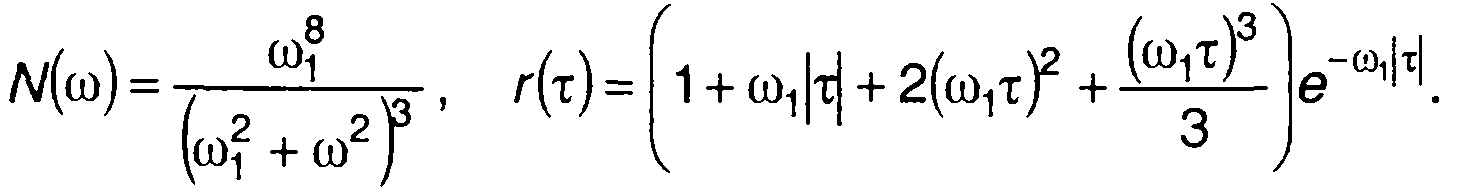
на рис. 20.12 - для характеристик - табл. 18.1, п.6

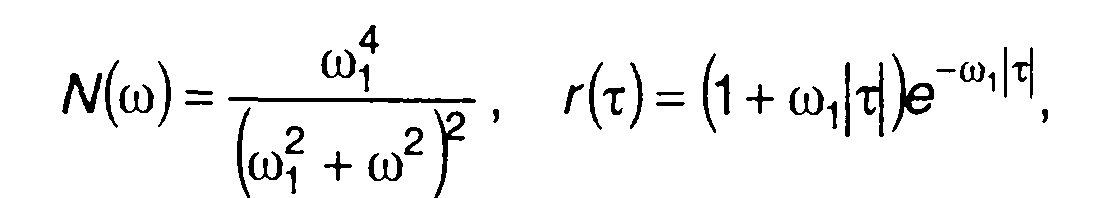
В табл. 20.2 изображены графики ПРВ и ФРВ частоты гауссов­ских процессов, характеристики которых приведены в табл. 18.1.

Период следования выбросов центрированного случайного процесса относительно нулевого уровня Т связан с частотой v со­отношением

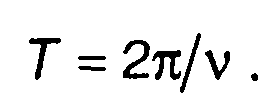(20.52)

Для гауссовского процесса длительности положительных и от­рицательных выбросов в среднем равны и связаны с частотой со­отношением

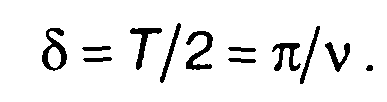(20.53)

С учетом (20.52) и (20.53) выражения для ПРВ периода и дли­тельности выбросов случайного процесса определим через ПРВ частоты в виде

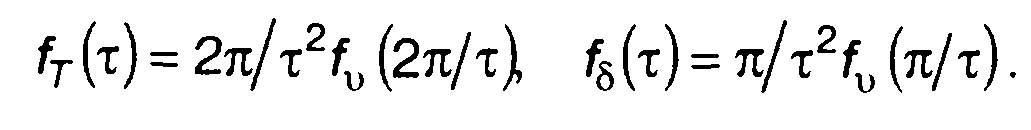(20.54)

Исходя из (20.54) запишем выражения для f_T(τ) и f_δ(τ) с исполь­зованием г_п(т)

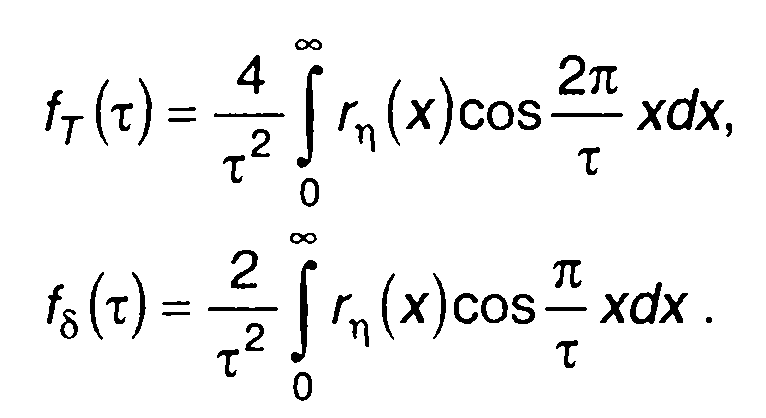(20.55)

Таблица 20.2.

Плотность и функция распределения вероятностей частоты гауссовского процесса

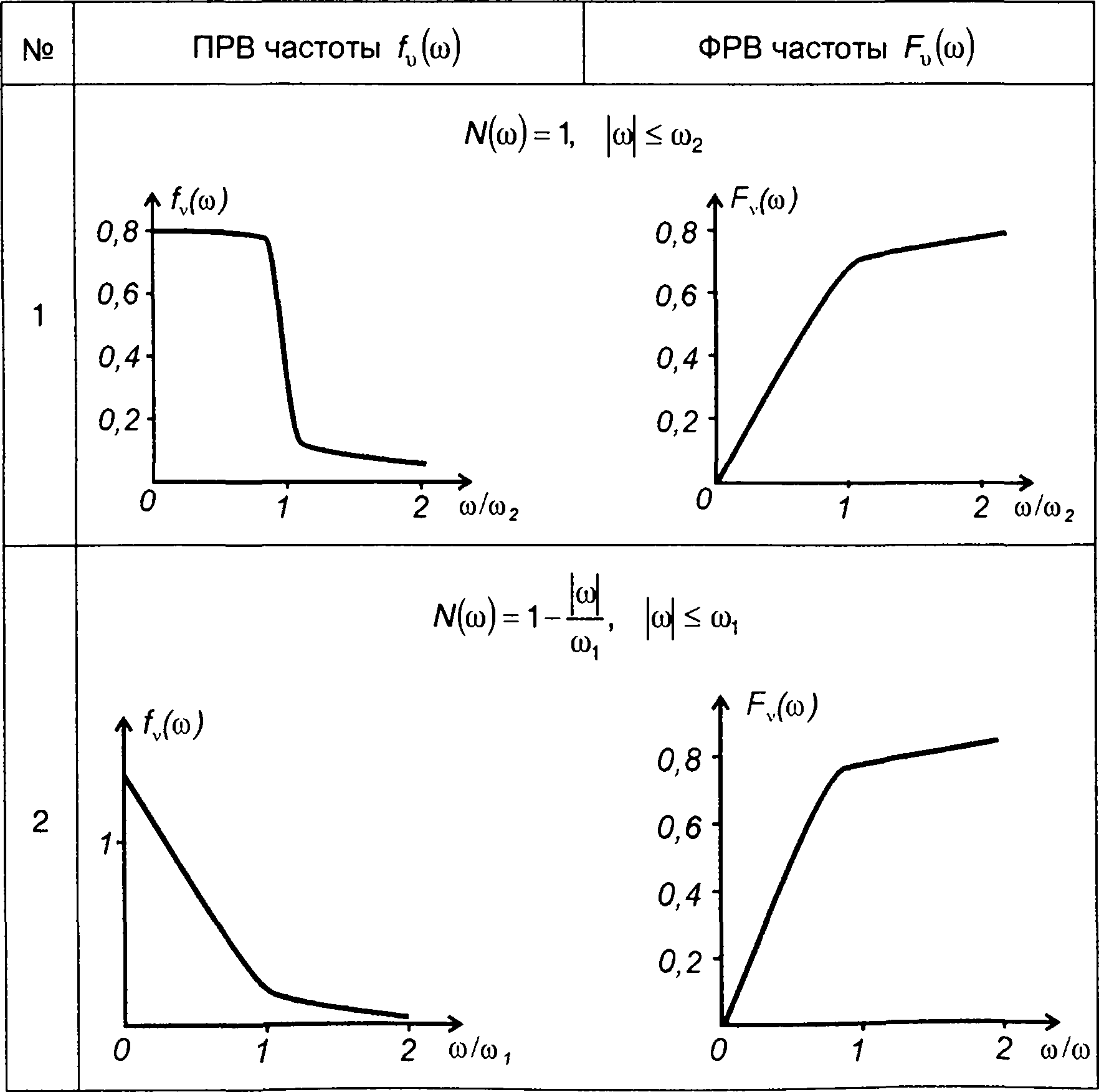
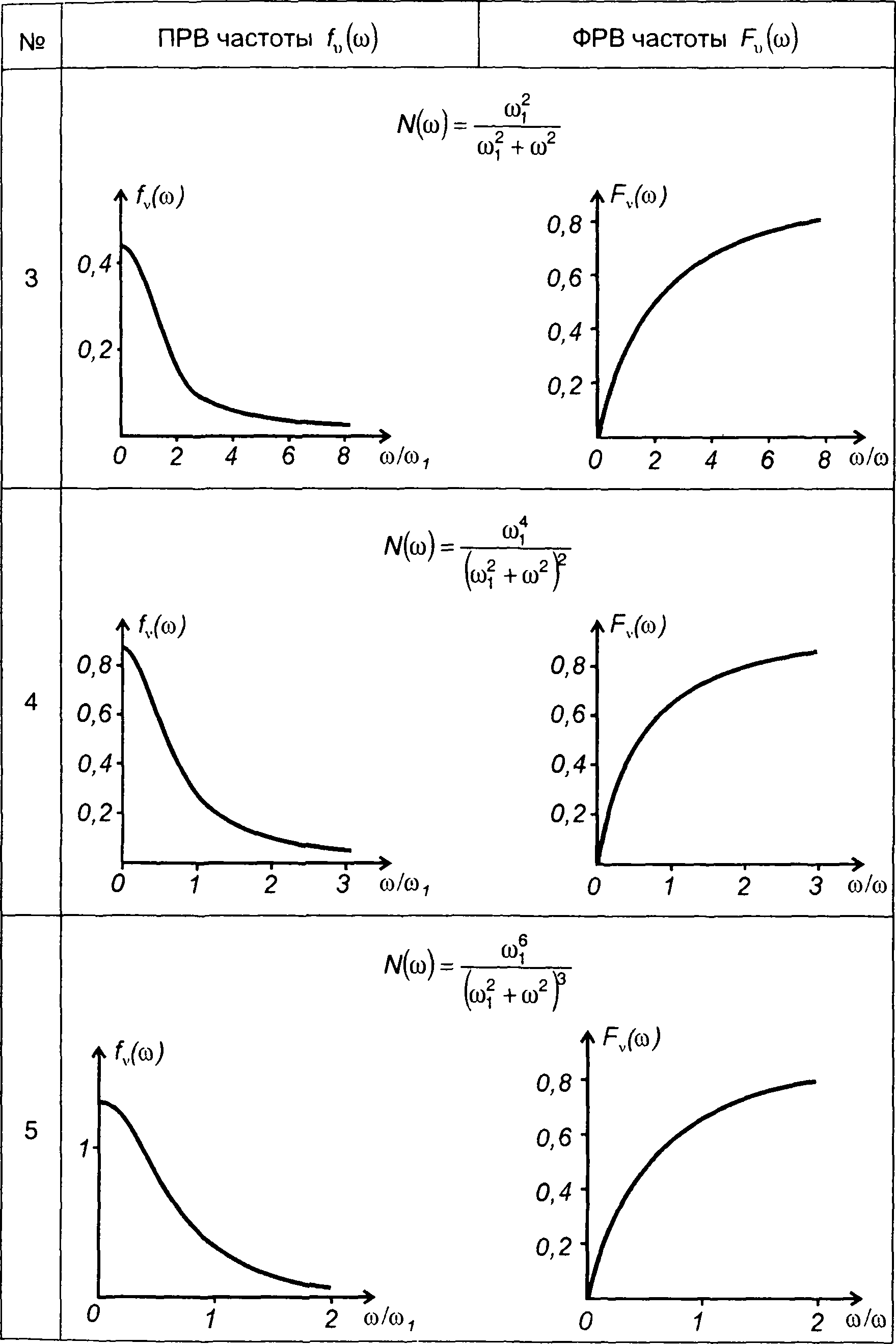
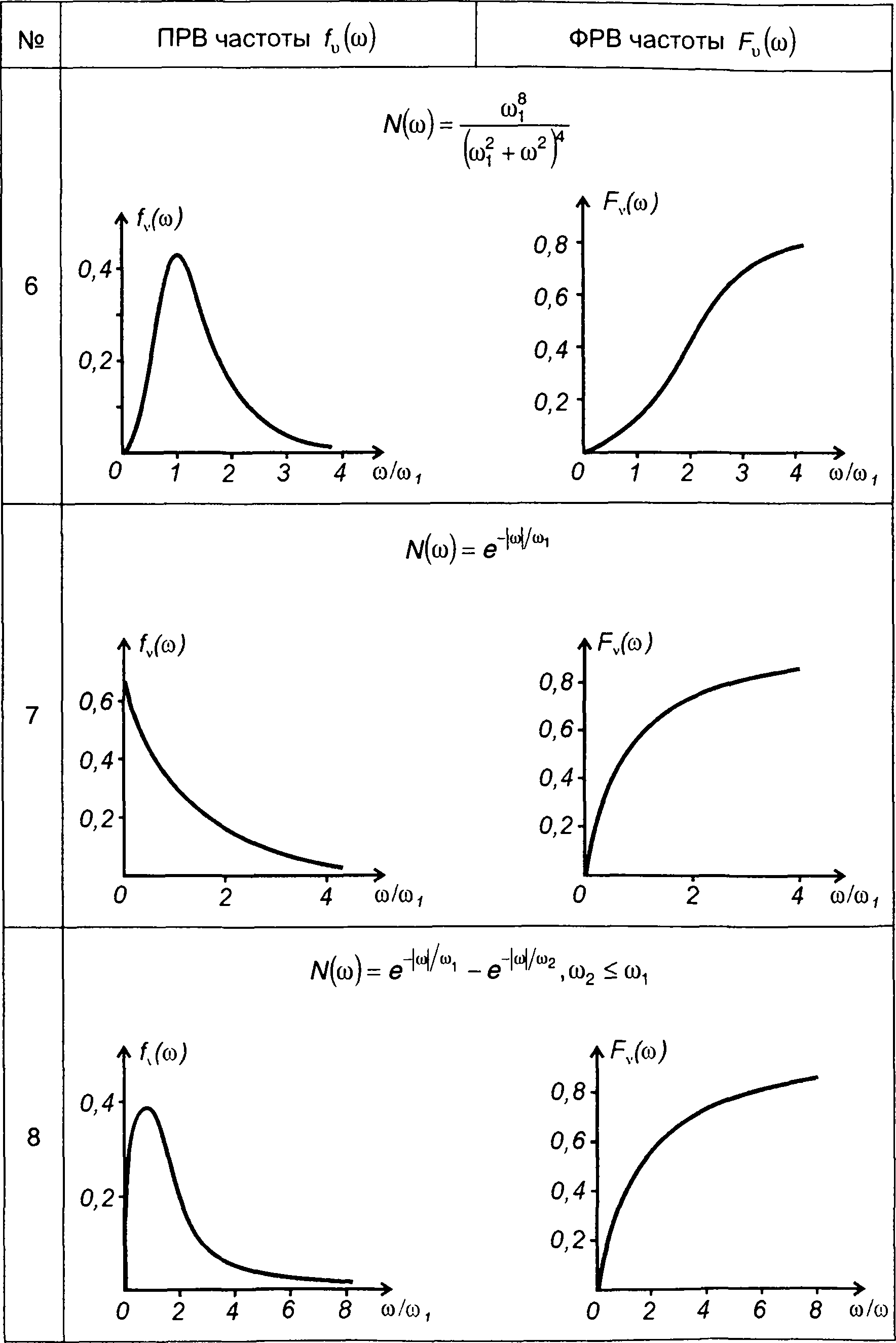
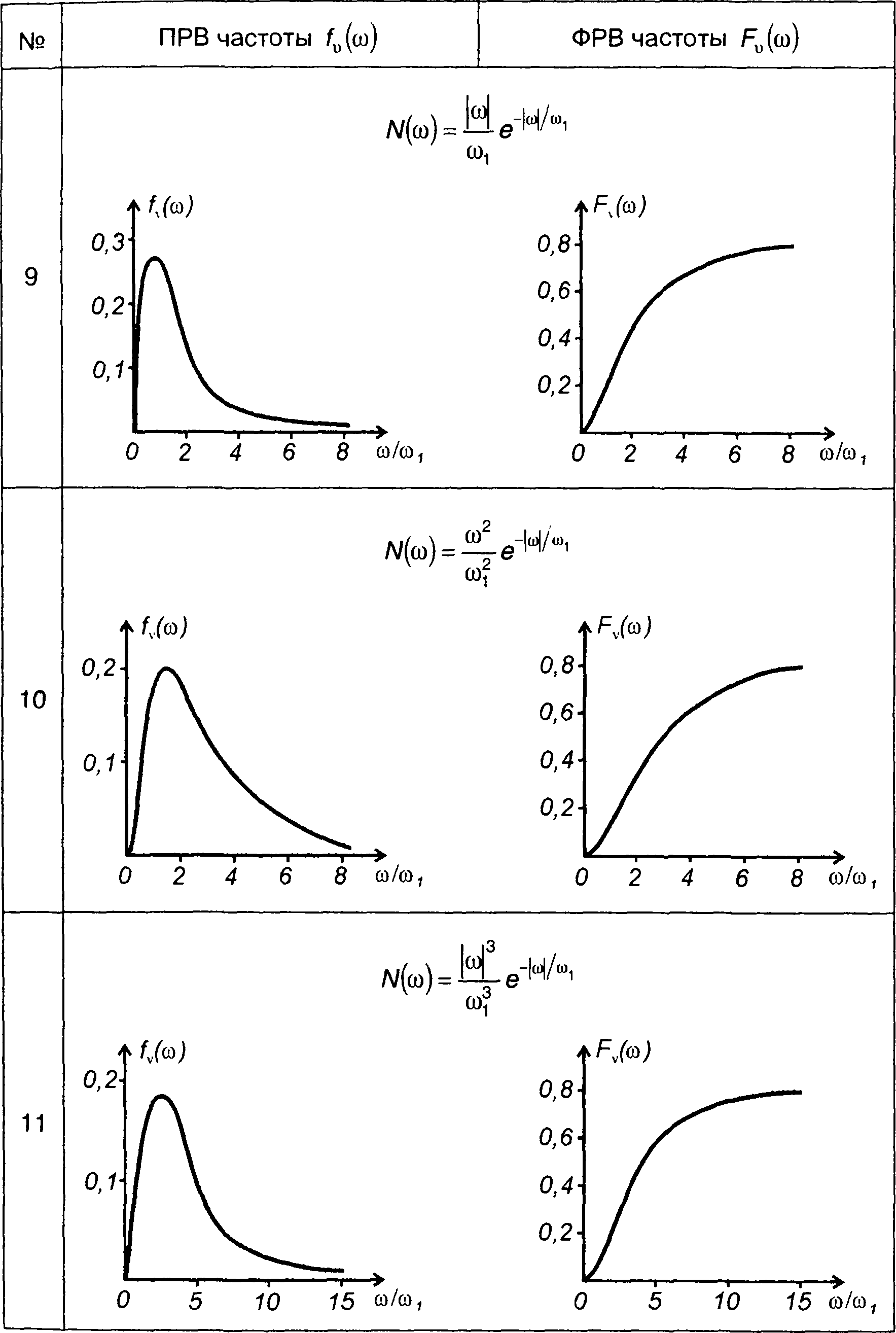
Для гауссовского процесса получим

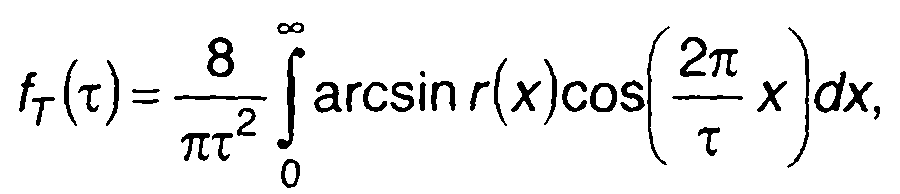(20.56)

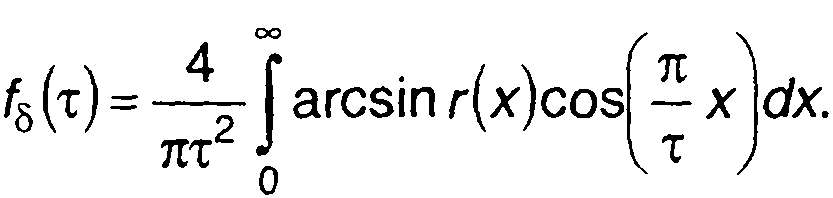(20.57)

В качестве примера рассмотрим гауссовский процесс, имеющий корреляционную функцию вида (рис. 20.9,а)

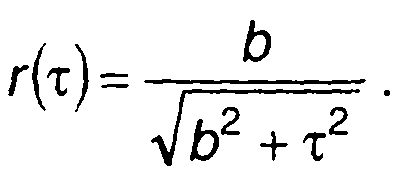
Исходя из (20.56) и учитывая результат ранее решенного при­мера, получим

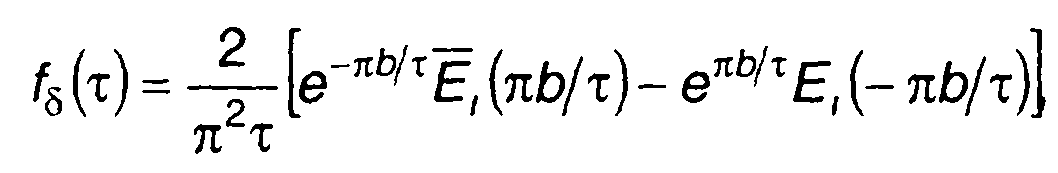
где Е(х) - интегральная показательная функция.

При расчете ПРВ (ФРВ) длительности выбросов гауссовского процесса можно воспользоваться разложением arcsin r(т) в ряд

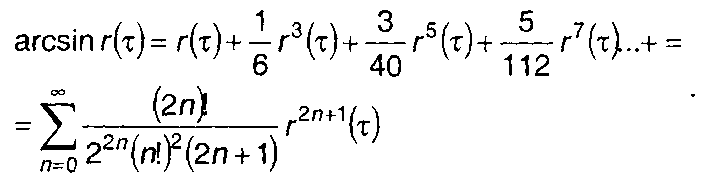(20.58)

После подстановки (20.58) в (20.57) получим

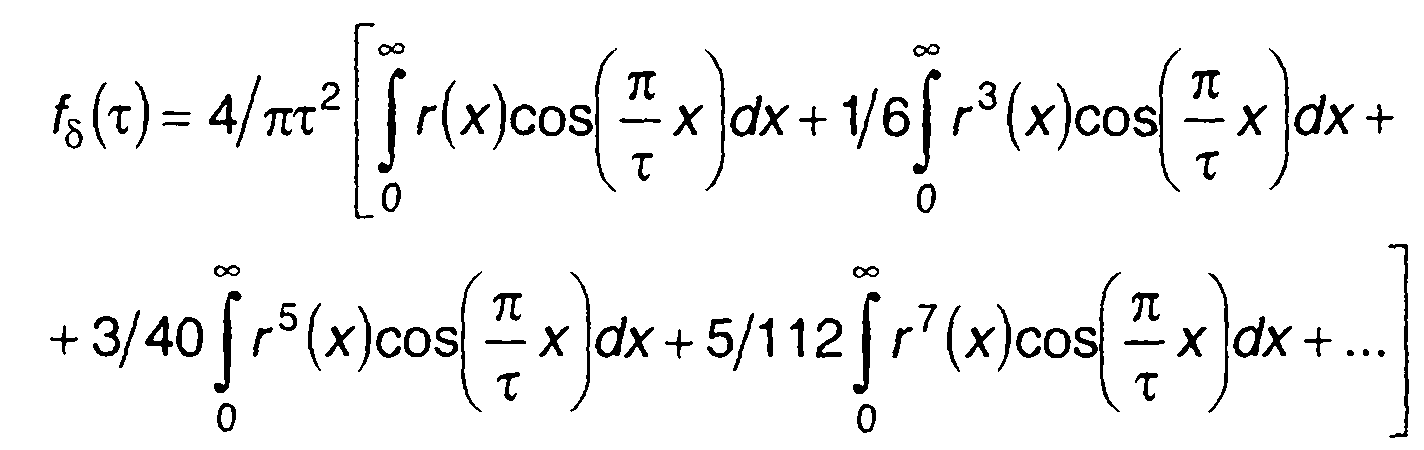(20.59)

или

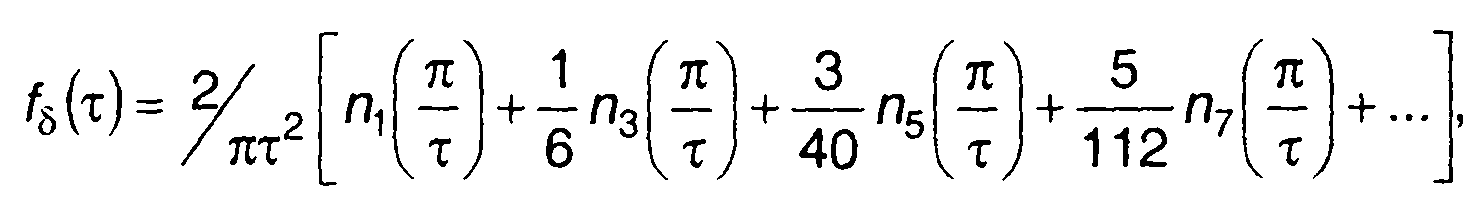
где

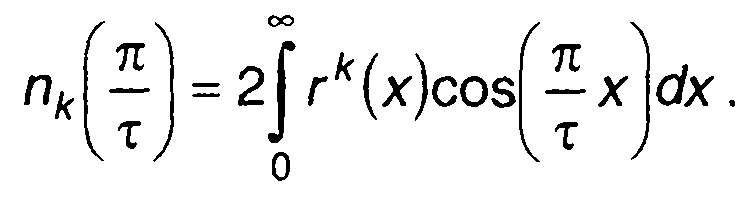(20.60)

Так при 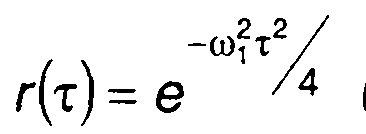(20.60) примет вид

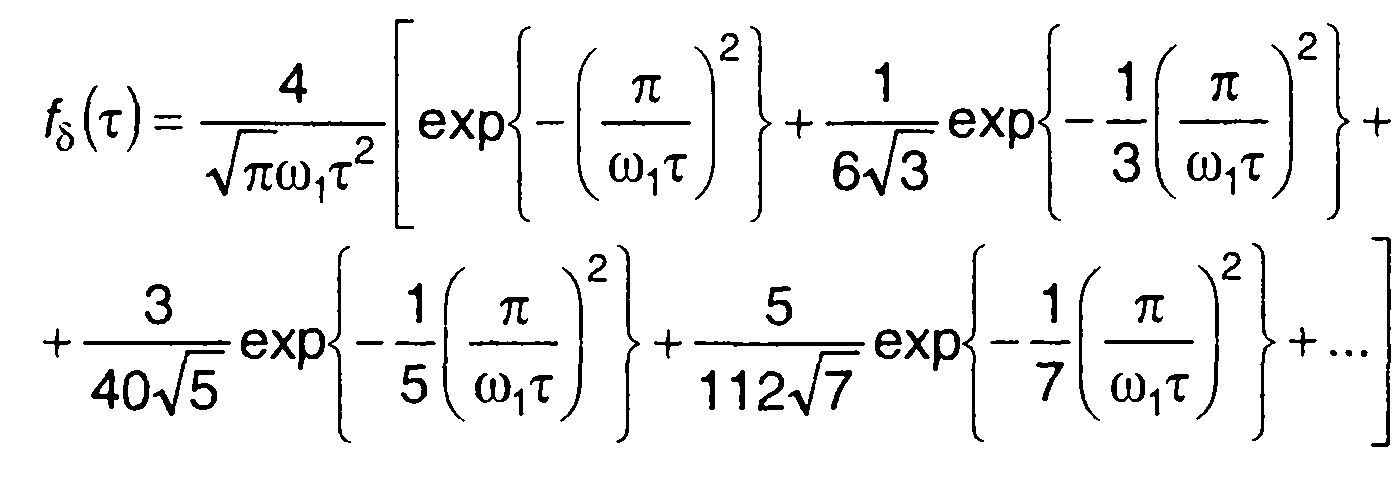
или

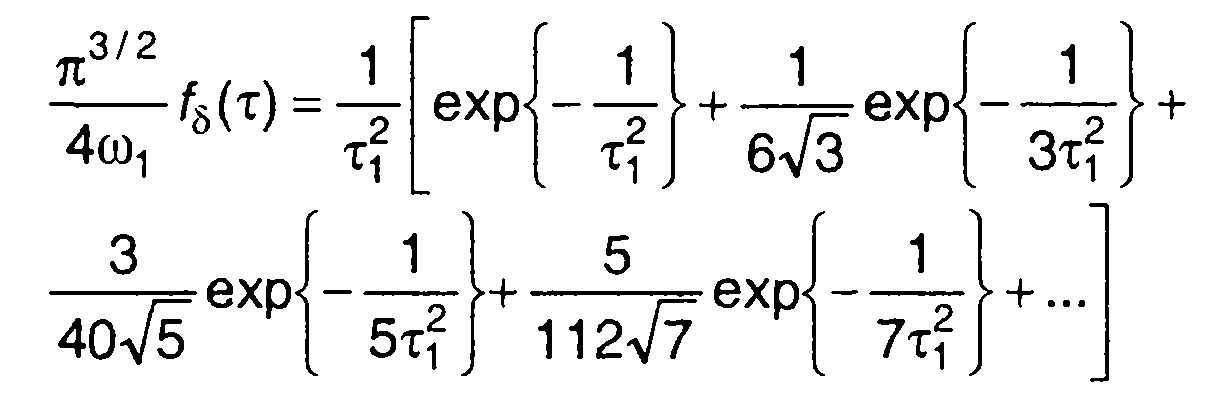
где т₁ = тω₁ / π.

Графики ПРВ и ФРВ длительности выбросов гауссовского про­цесса с рассматриваемой характеристикой приведены на рис. 20.13,а,б. На рис. 20.13, пунктирной линией проведены графи­ки ПРВ и ФРВ длительности выбросов, полученный с использова­нием методики, изложенной в п. 20.1. Сравнение графиков позво­ляет оценить ошибку, появляющуюся при использовании прибли­женного метода.

Графики ПРВ и ФРВ длительности выбросов центрированных гауссовских процессов для нулевого уровня и некоторых характе­ристик (спектра или корреляционной функции) изображены на рис. 20.14-20.16.

Для характеристик - табл. 18.1, п.4

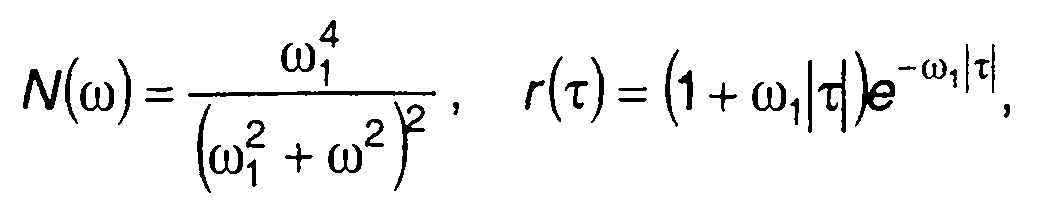
на рис. 20.14.

Для характеристик - табл. 18.1, п.5

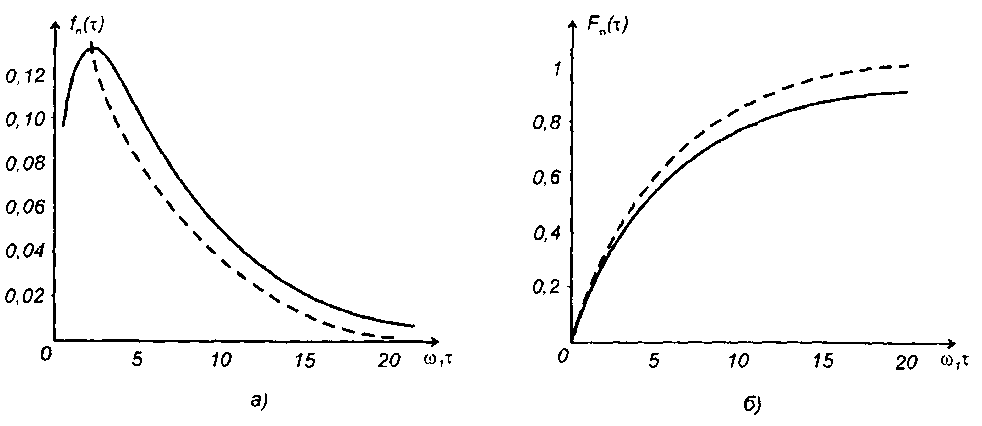
Рис. 20.13

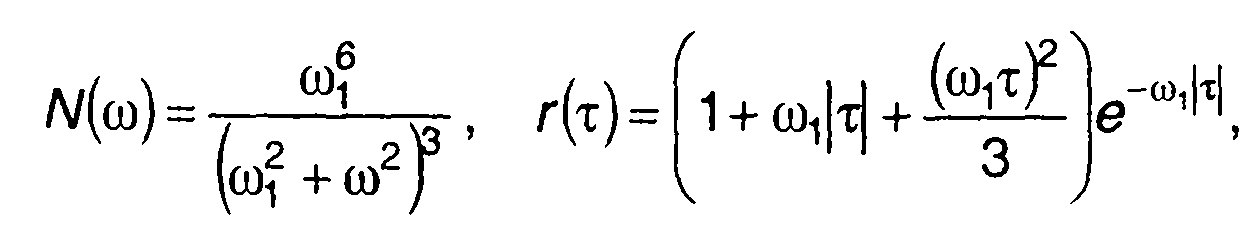
на рис.20.15.

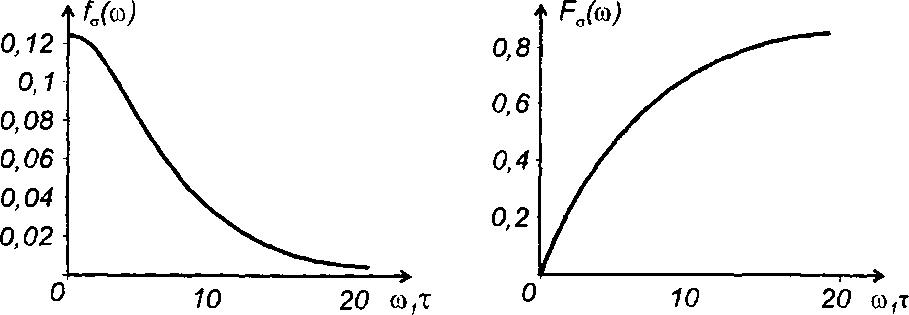
Рис. 20.15

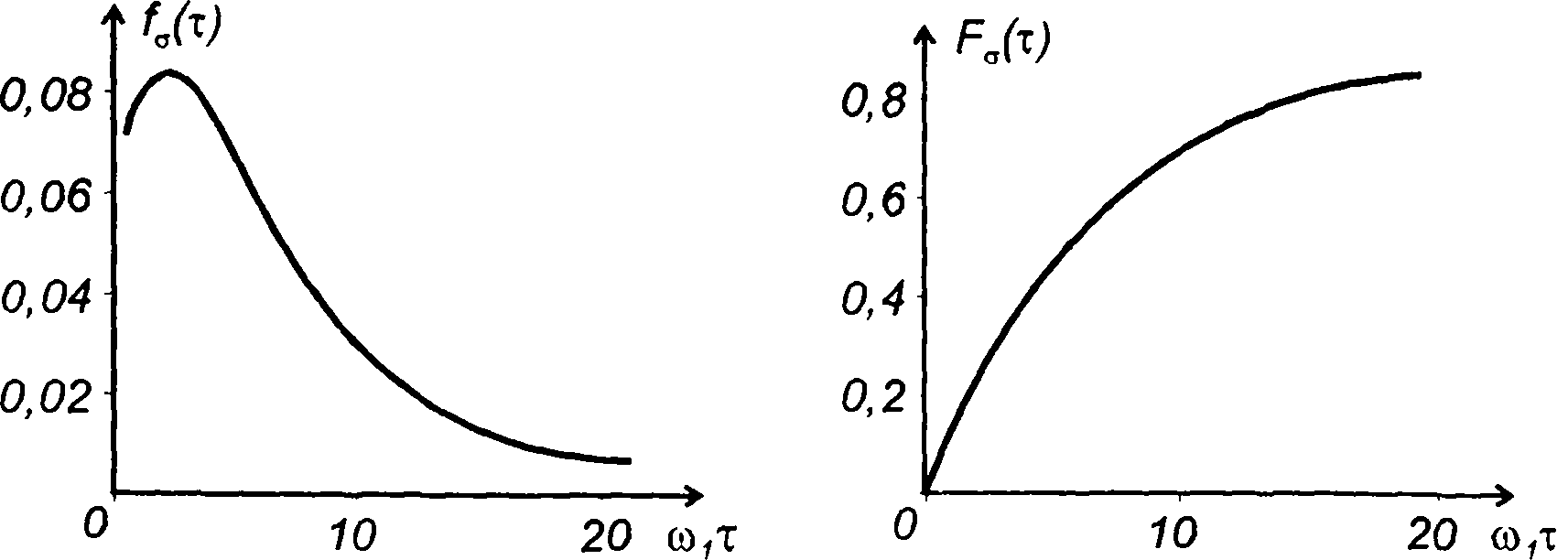
Рис. 20.14

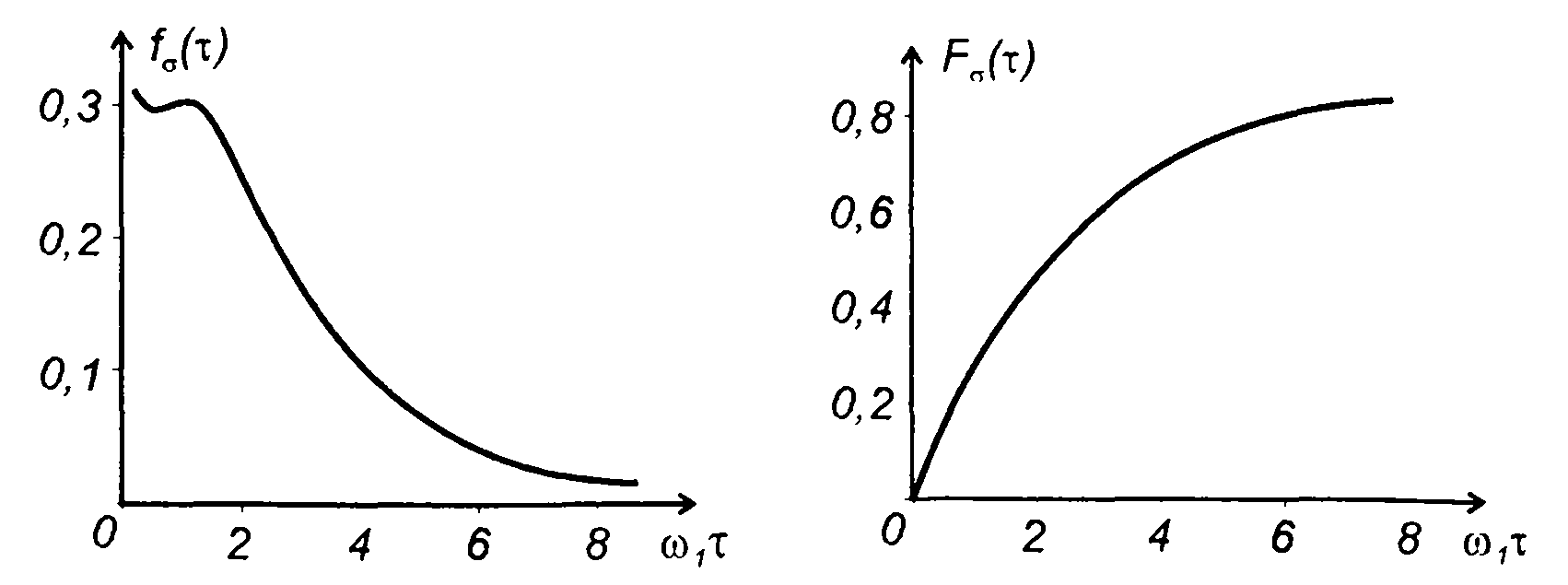
Рис.20.16

Для характеристик - табл. 18.1, п.6 на рис.20.16.

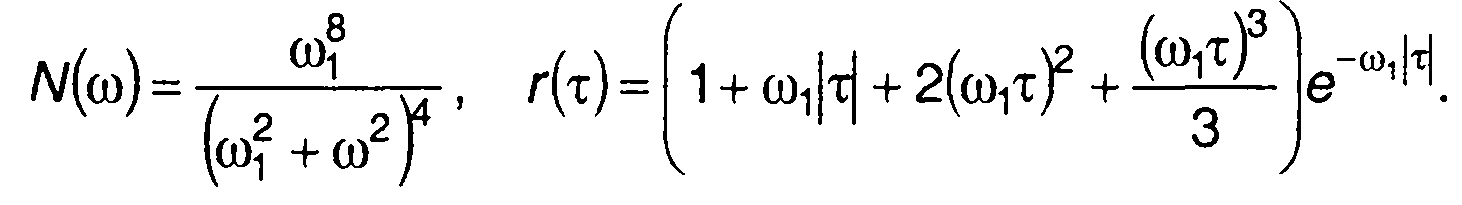
Вид графиков ПРВ длительности выбросов (рис.20.14 - 20.16), соответствует результатам экспериментального определения ПРВ случайных процессов, имеющих те же характеристики [20].

Графики ПРВ и ФРВ длительности выбросов гауссовских про­цессов с различными характеристиками (табл. 18.1), полученные с использованием описанного подхода, включены в табл. 20.3.

Все изложенное касалось распределения длительности выбро­сов центрированного гауссовского процесса относительно нулевого уровня. При уровне, отличном от нулевого, необходимо учитывать различие в длительности отрицательных и положительных выбро­сов. Можно считать, что в среднем длительность отрицательных выбросо вотносительно уровня х определяется как

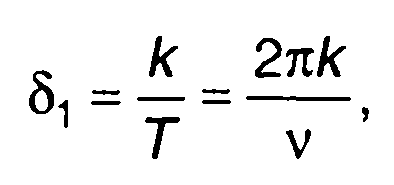(20.61)

где Т - период следования выбросов, определяемый как 2π/v, k= F₁(x), F₁(x) - одномерная ФРВ случайного процесса ξ(t).

Для положительных выбросов запишем

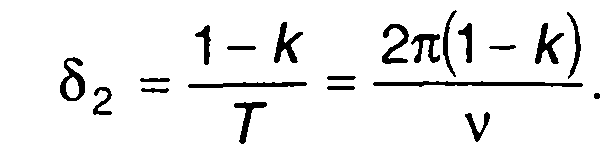(20.62)

Таким образом, зная распределение частоты случайного про­цесса, можно получить и распределение длительности отрица­тельных и положительных выбросов

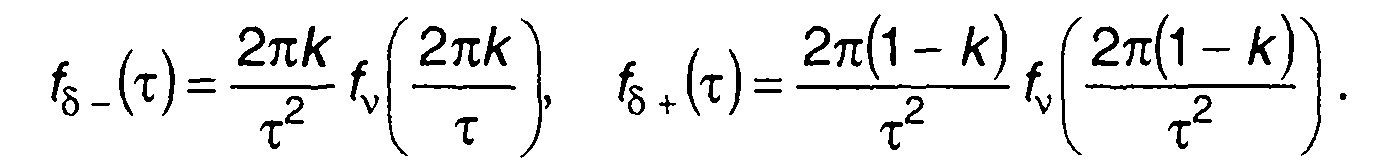(20.63)

Имея ПРВ длительности выбросов, можно определить и сред­нее значение длительности выбросов

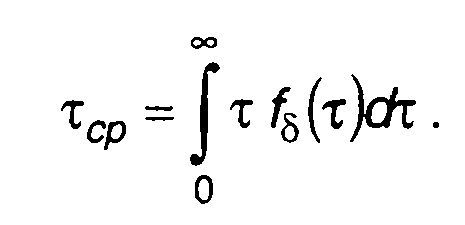(20.64)

Однако сложность выражений для ПРВ длительности выбросов заставляет выбрать несколько иной путь. Используя его, получим выражения для средней частоты следования выбросов и средней

Таблица 20.3.

Плотность и функция распределения вероятностей длительности выбросов гауссовского процесса

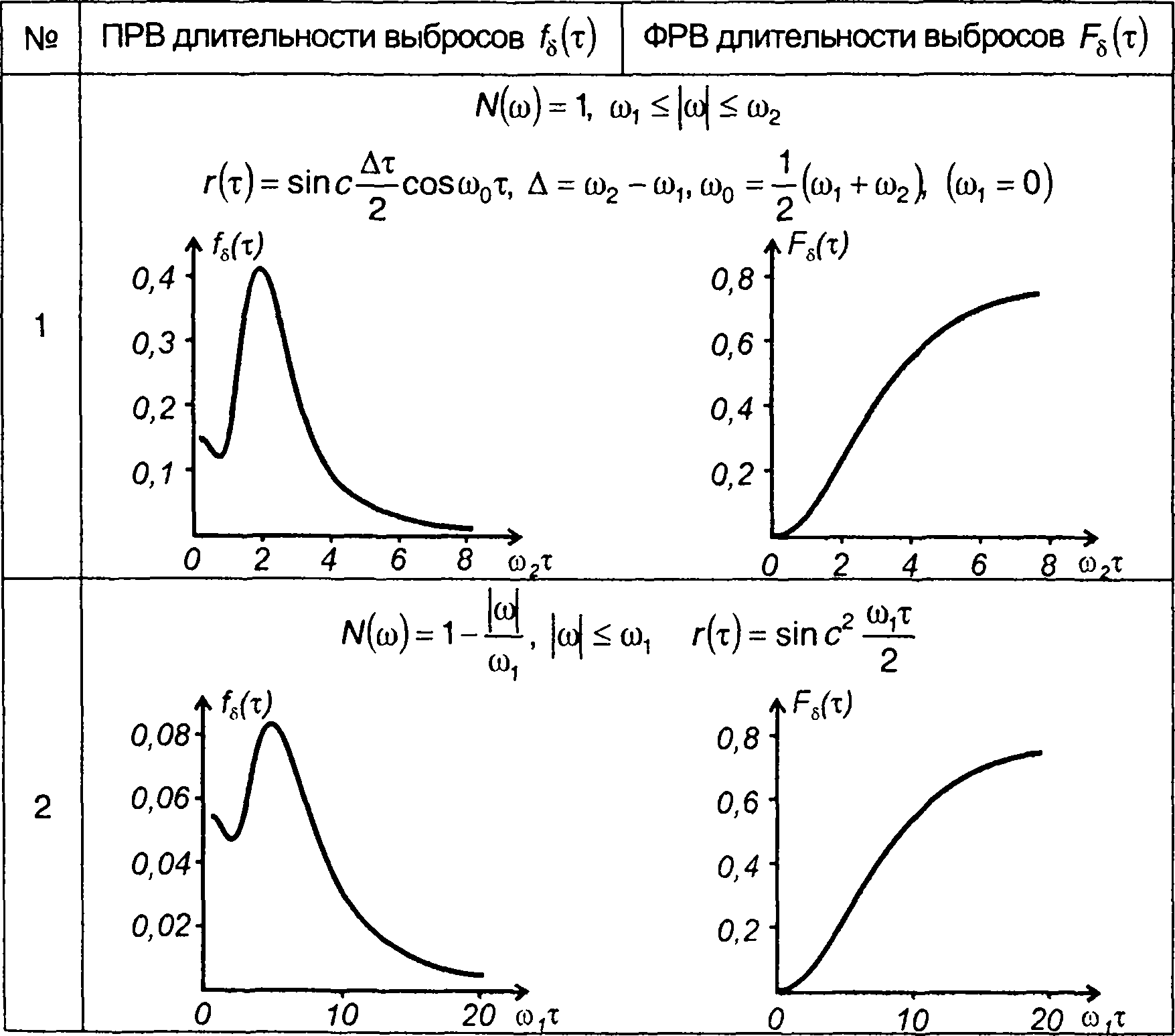
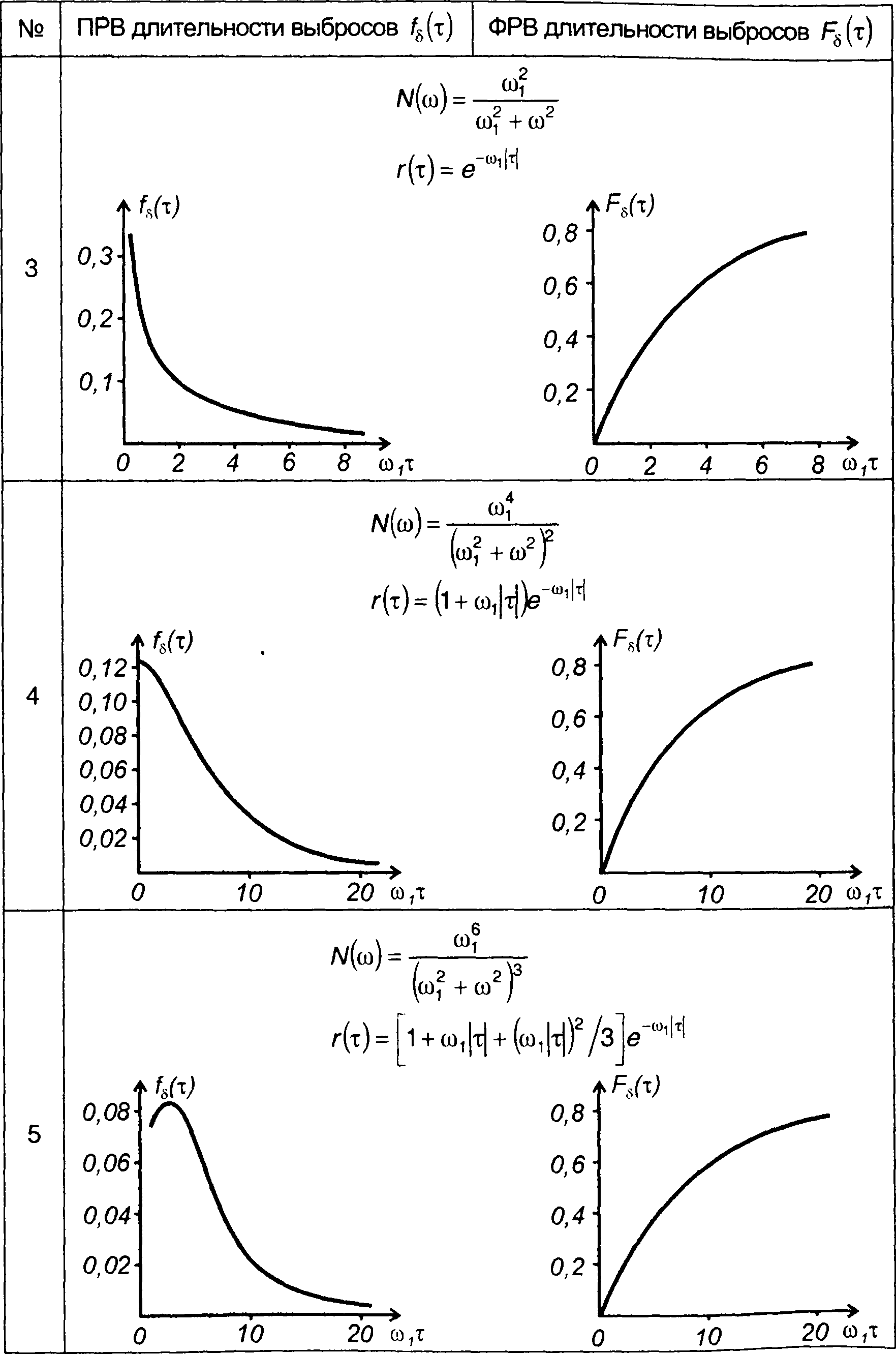
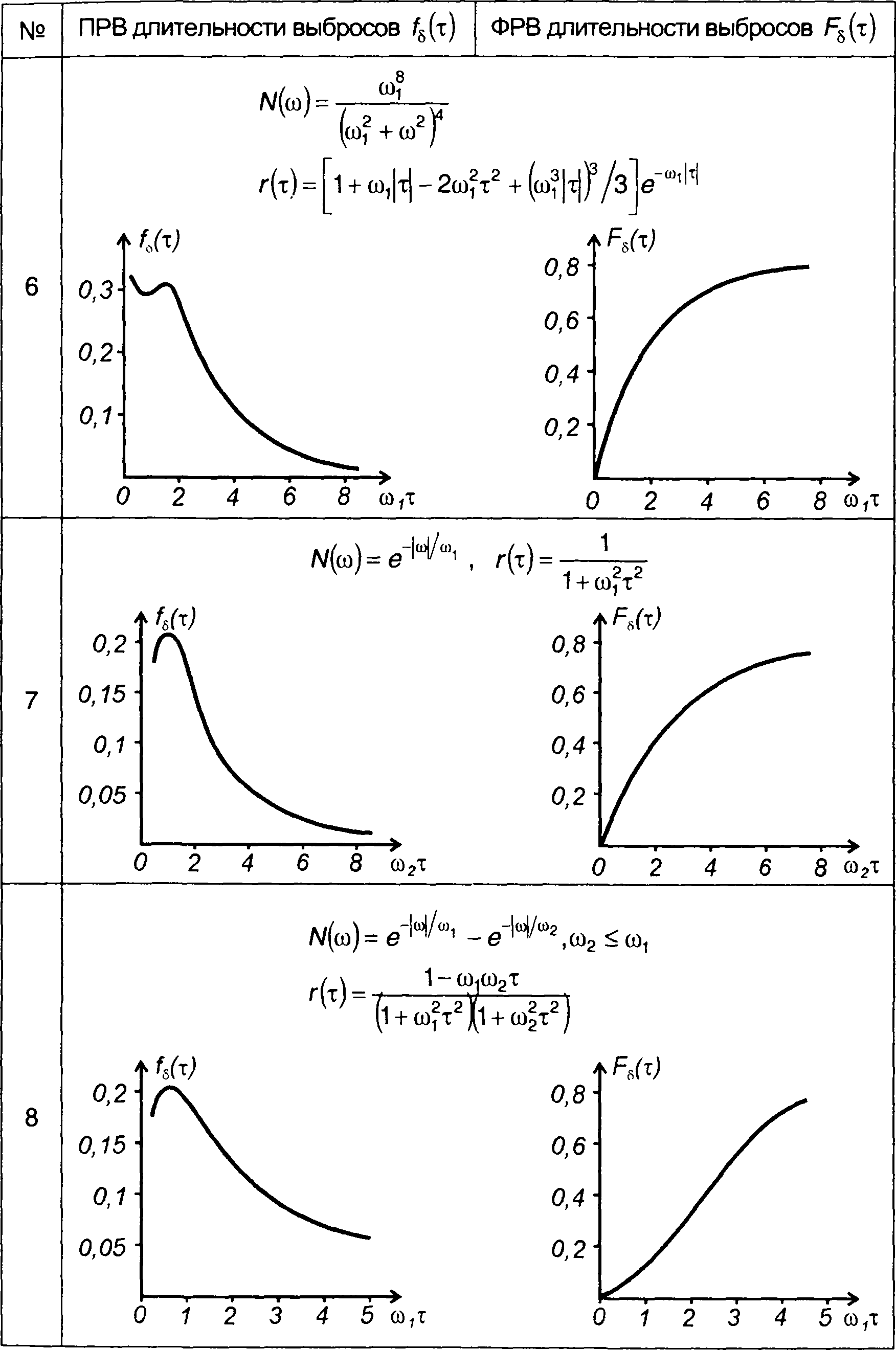
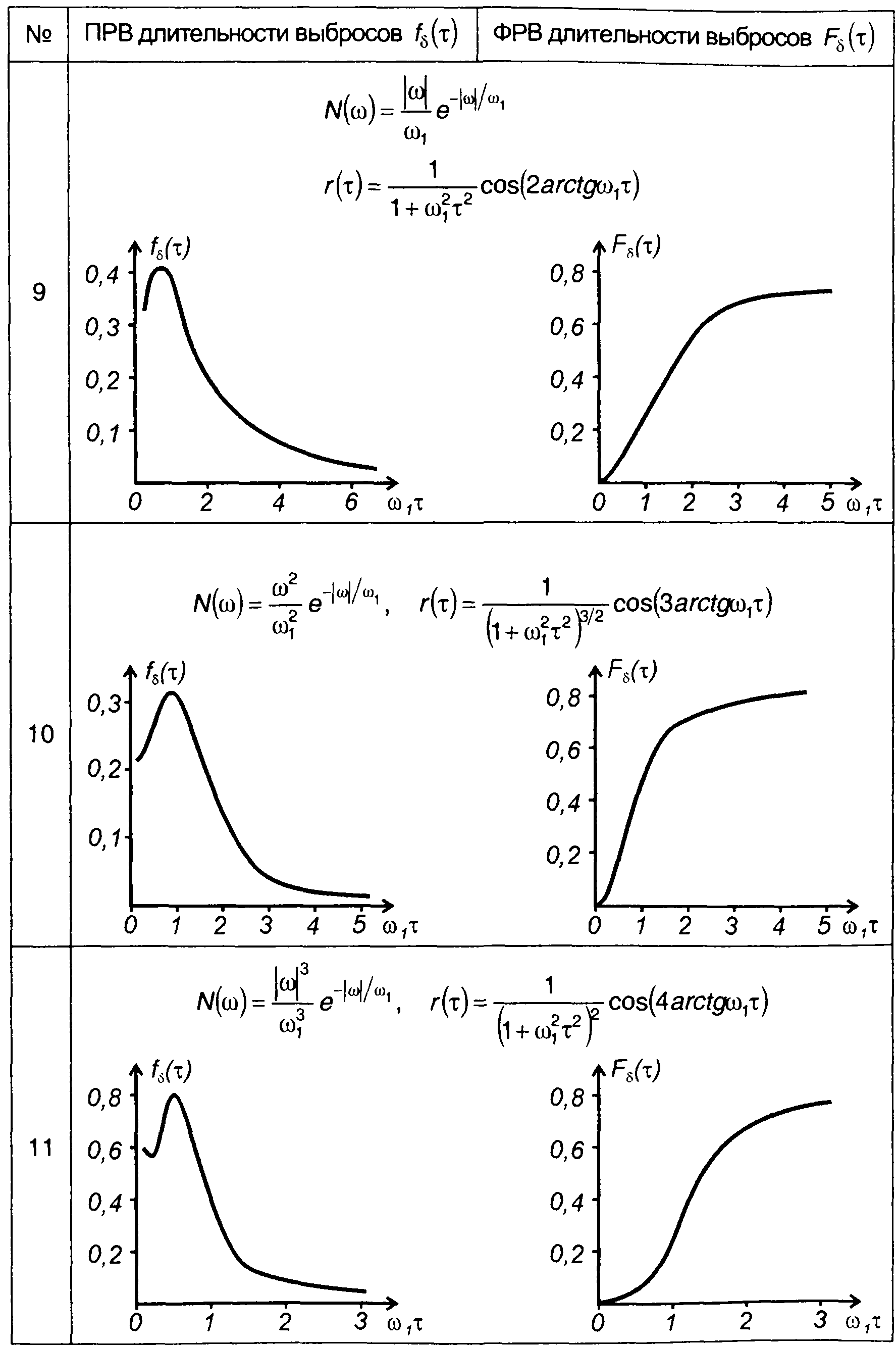
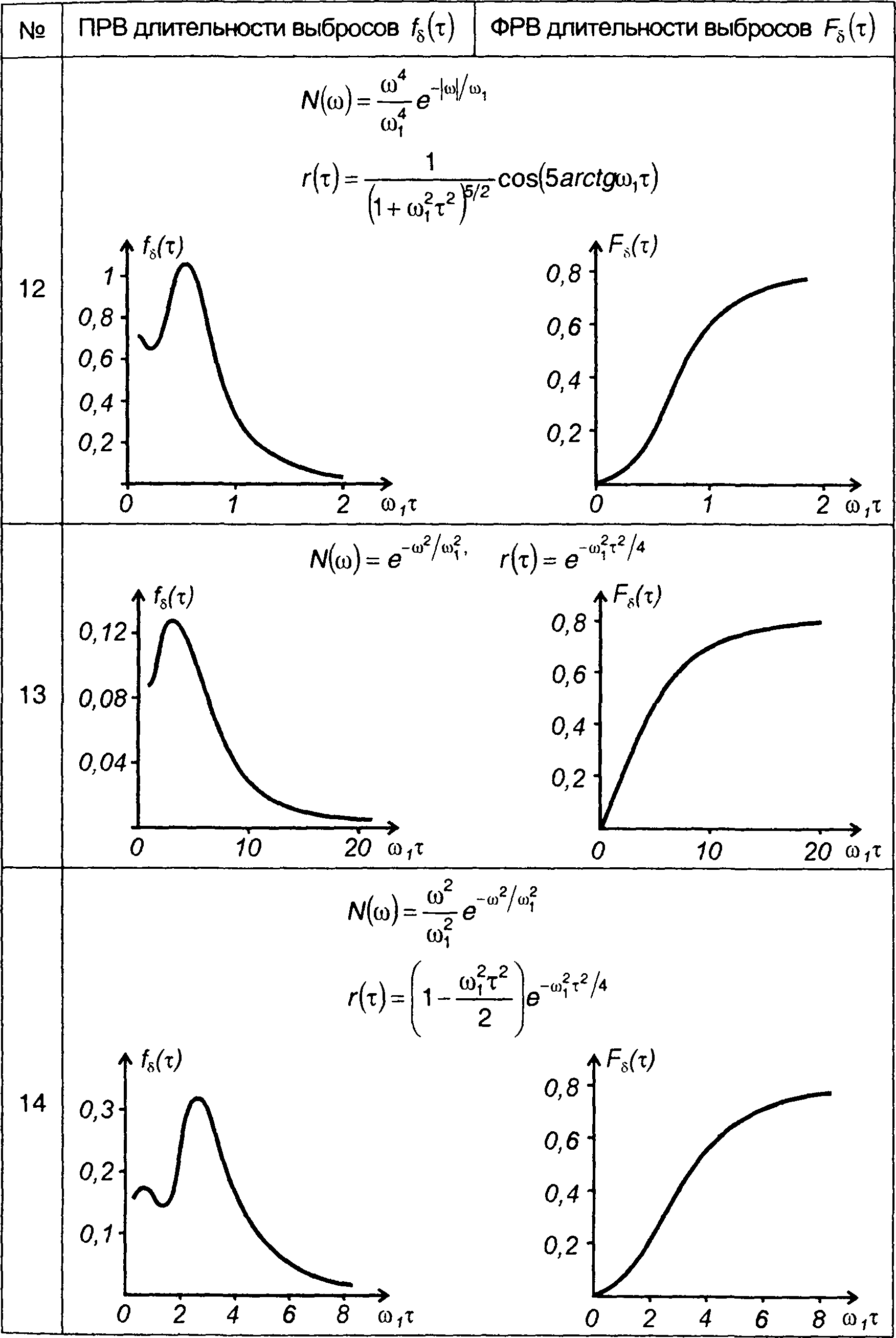
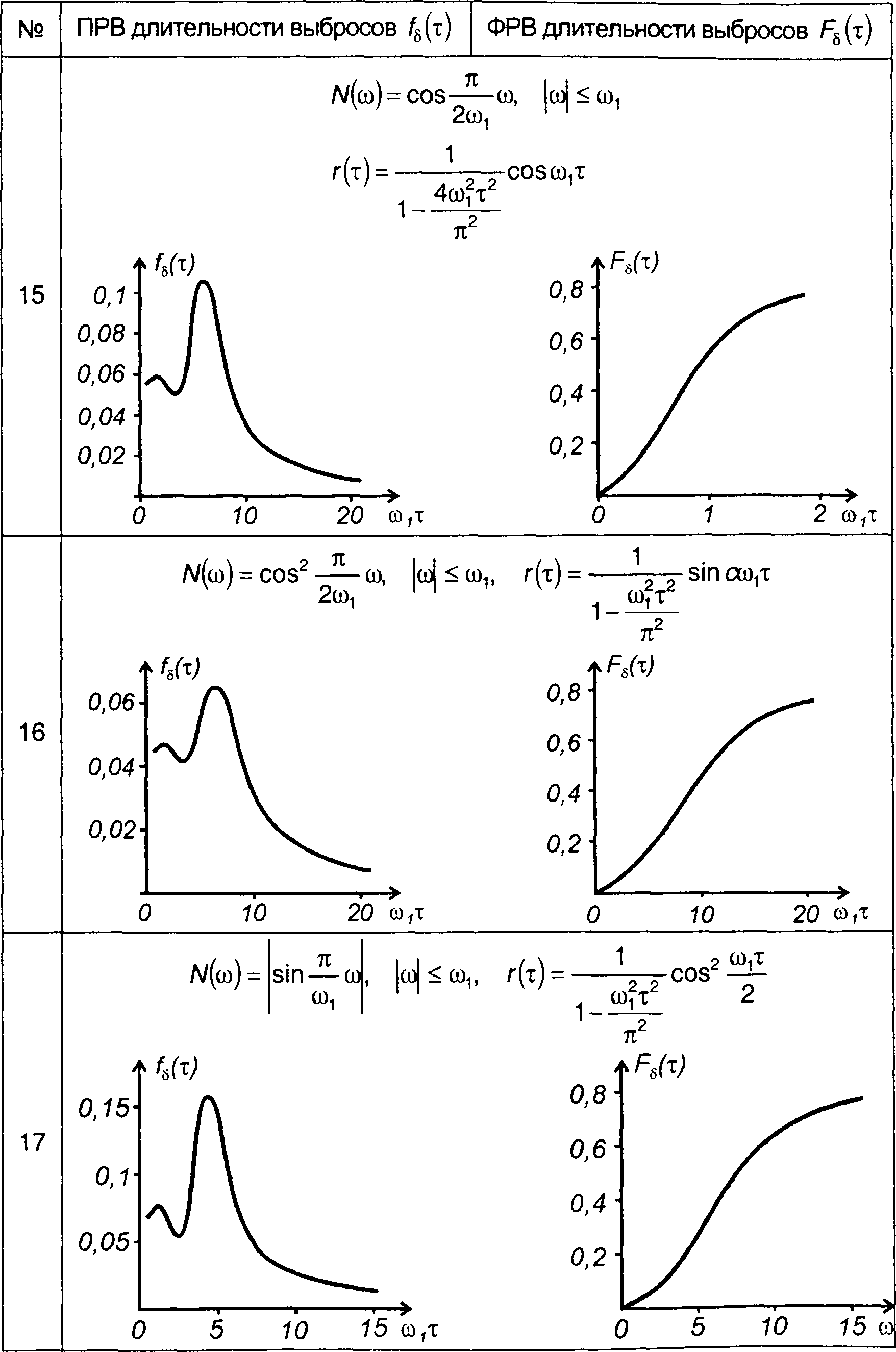
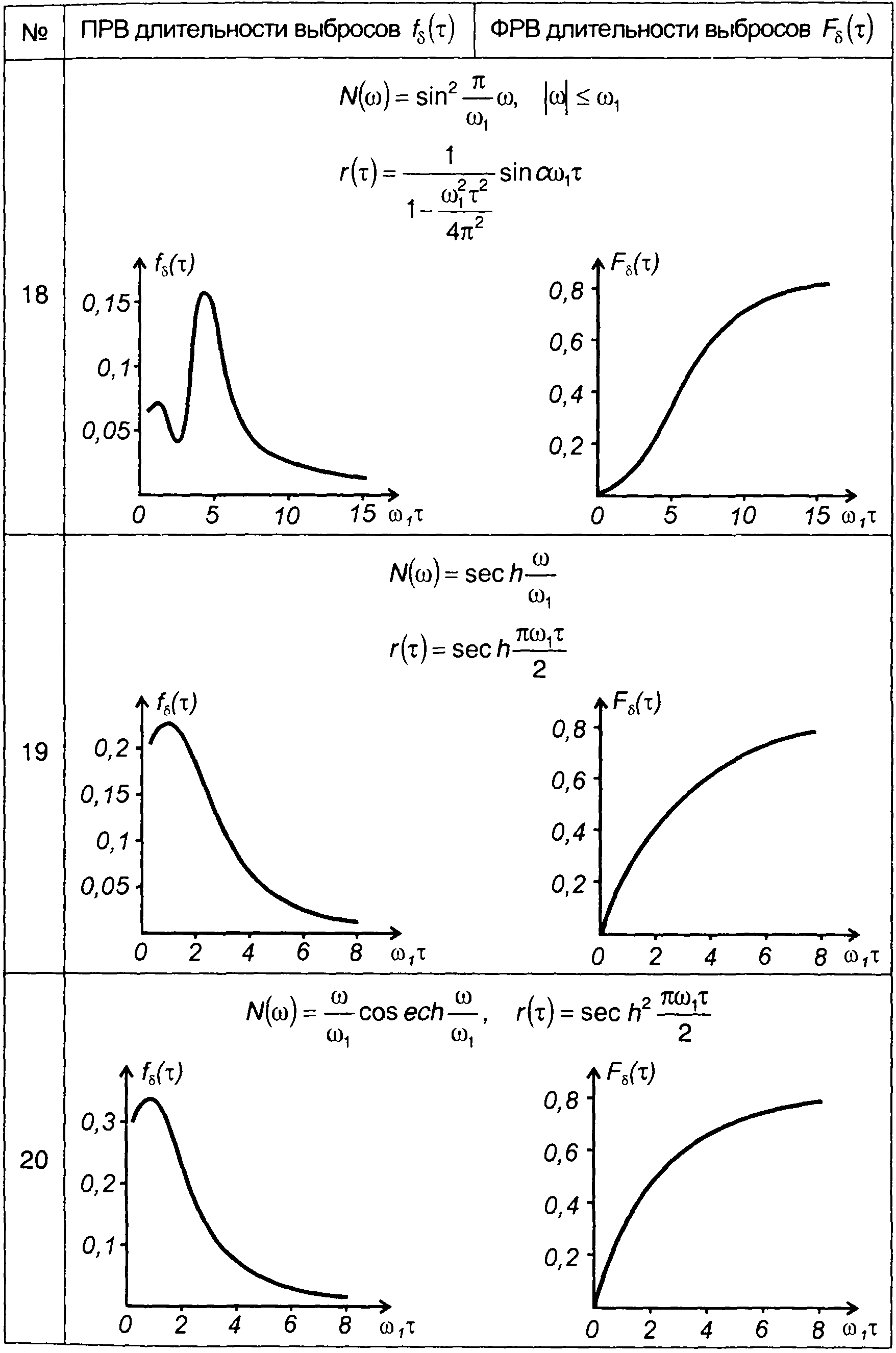
длительности выбросов гауссовского процесса относительно нуле­вого уровня.

20.2.3. Среднее значение длительности выбросов

Рассмотрим случайный процесс η(t) - центрированный гаус­совский процесс на выходе идеального ограничителя в моменты времени t₁ и t₂(t₂ t₁= ∆t). Случайный процесс в моменты време­ни t₁ и t₂ принимает значения ±1. Полная группа событий описы­вается вероятностями:

Р ++ - вероятность превышения нулевого уровня в моменты времени t₁ и t₂ ;

Р -- - вероятность непревышения нулевого уровня в моменты времени t₁ и t₂ ;

Р+- - вероятность превышения нулевого уровня в момент вре­мени t₁ и непревышения в момент времени t₂;

Р- + - вероятность непревышения нулевого уровня в момент времени t₁ и превышения в момент времени t₂.

Очевидно,

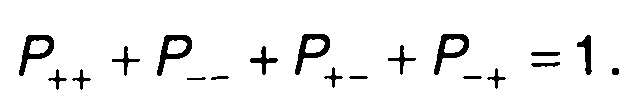(20.65)

Корреляционная функция случайного процесса η(t) определя­ется выражением

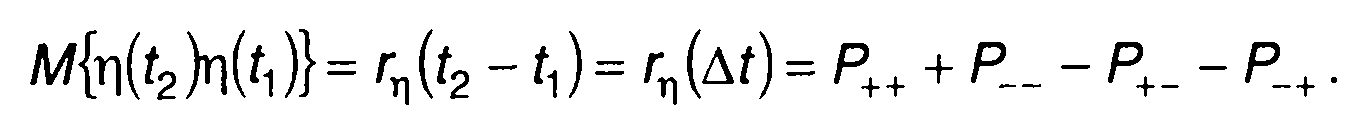(20.66)

Учитывая для гауссовского процесса равенство

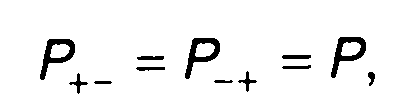(20.67)

из (20.65) и (20.66) получим выражение для вероятности несовпа­дения знаков случайного процесса в моменты времени t₁ и t₂ ;

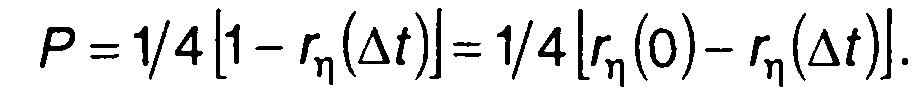(20.68)

Величина

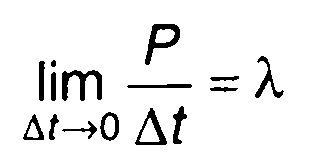(20.69)

представляет среднюю частоту следования выбросов случайного

процесса (подробнее см. п. 20.3). С учетом (20.68) запишем

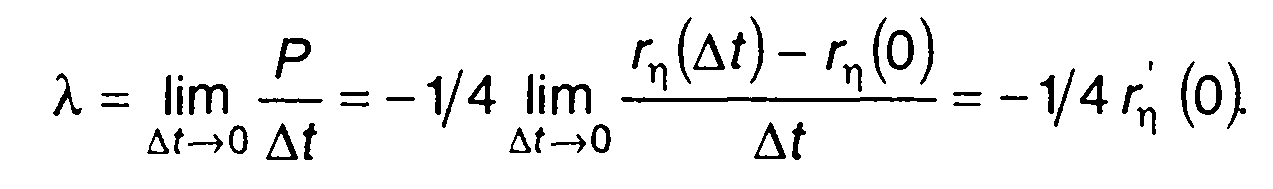(20.70)

С учетом (20.50) получим

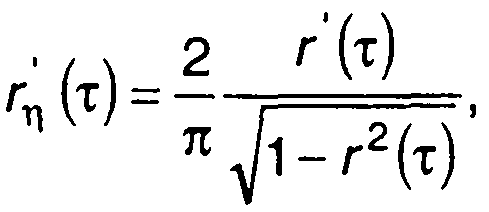(20.71)

где r(т) - нормированная корреляционная функция исходного слу­чайного процесса ξ(t).

Предел в (20.71) при т → 0 найдем, применяя правило Лопиталя

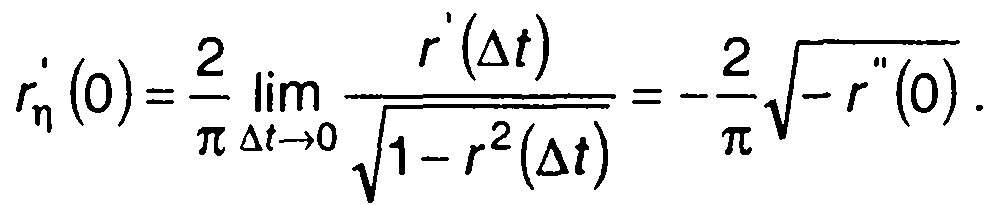(20.72)

Подставляя (20.72) в (20.70), запишем

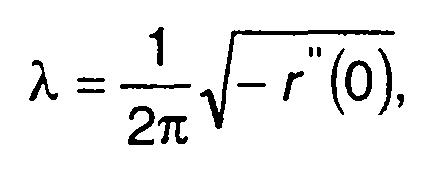(20.73)

что совпадает с результатом, полученным ранее.

Среднее значение длительности выбросов относительно нуле­вого уровня равно

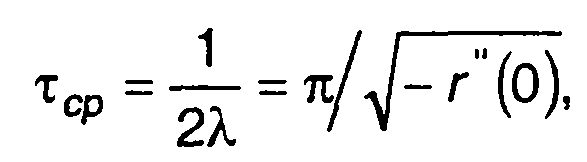(20.74)

что совпадает с (20.16).

Приведенные соотношения, связывающие ПРВ длительности выбросов и частотные характеристики случайного процесса, могут быть использованы и при решении обратной задачи - определении спектра случайного процесса по ПРВ длительности выбросов. Та­кая задача возникает, например, при экспериментальной обработ­ке реализации случайного процесса, когда в качестве исходной характеристики наиболее просто получить ПРВ длительности вы­бросов.

20.2.4. Решение обратной задачи

ПРВ частоты случайного процесса связана с ПРВ периода вы­бросов соотношением

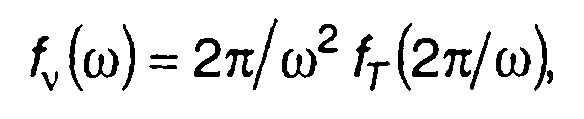(20.75)

где f_T (т) - ПРВ периода выбросов, которая может быть получена аналогично (20.54).

Плотность распределения вероятностей частоты описывает нормированную спектральную плотность мощности случайного процесса на выходе идеального ограничителя

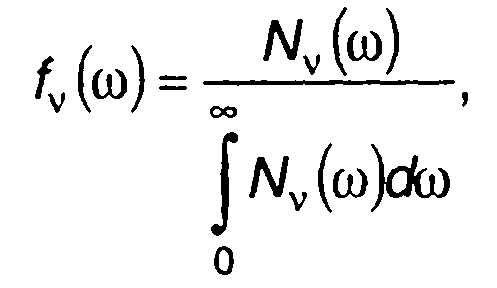(20.76)

характеризует спектр исходного случайного процесса.

Для гауссовского процесса от N_η(ω) перейдем к корреляцион­ной функции случайного процесса

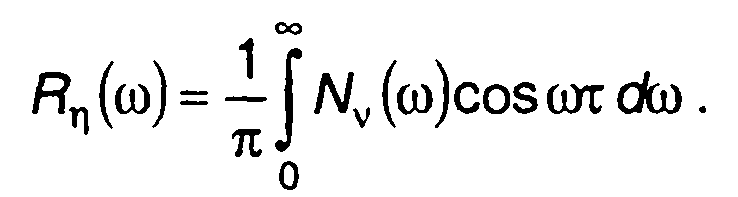(20.77)

Используя соотношение, связывающее r_η(т) с нормированной корреляционной функцией исходного случайного процесса r(т):

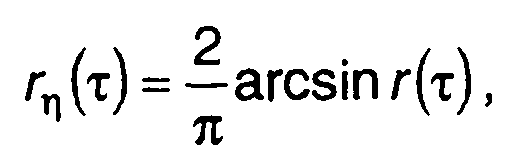(20.78)

можно получить корреляционную функцию и спектр исходного случайного процесса

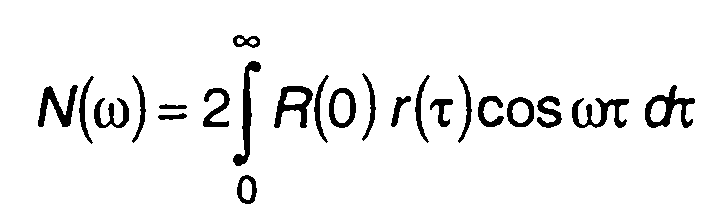(20.79)

В качестве примера рассмотрим случайный процесс, для кото­рого ПРВ периода выбросов имеет вид

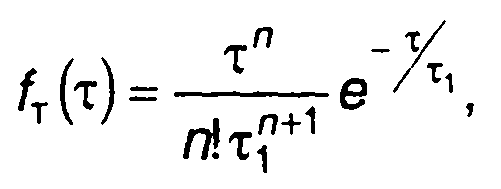
где т₁ = const, n = 1,2,...

Из (20.75) получим

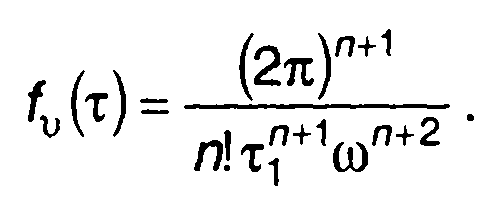
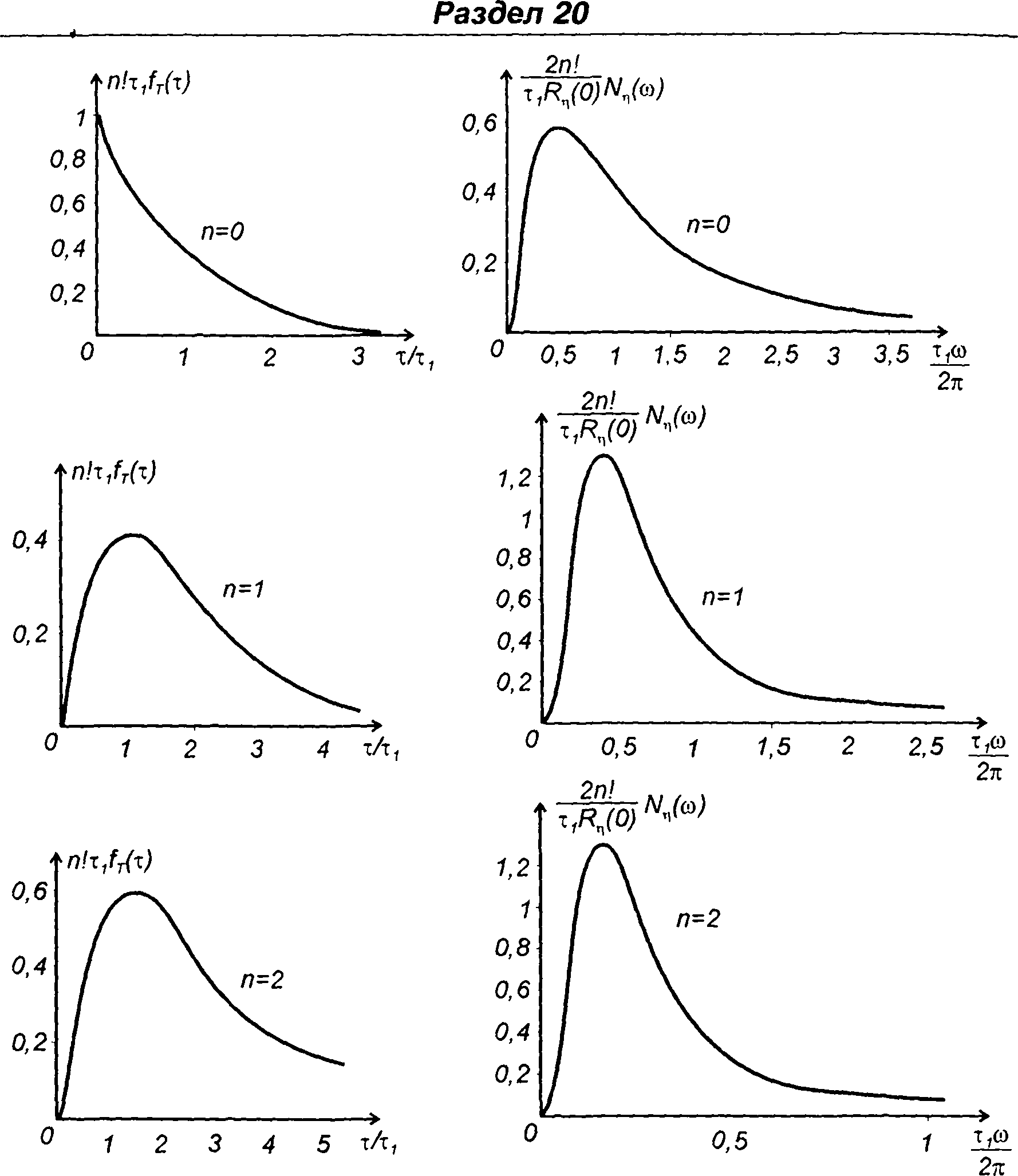
Рис.20.17

С учетом (20.76) найдем (рис. 20.17)

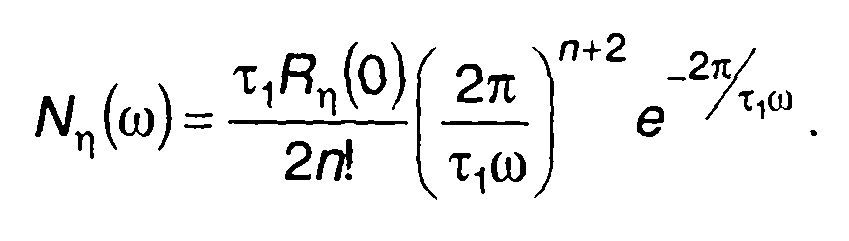
Величина N_η(ω) дает представление о спектре случайного про­цесса, от нее можно перейти к спектру исходного случайного про­цесса.

20.3. Средняя частота следования и средняя длитель­ность выбросов случайного процесса

Имея ФРВ или ПРВ длительности выбросов, можно определить математическое ожидание - среднюю длительность выбросов и другие моменты распределения. С учетом того, что ранее было по­лучено приближенное решение для ПРВ длительности выбросов (п. 20.1) и решение для ограниченных условий (п. 20.2), целесообраз­но задачу по определению моментных характеристик выбросов рас­смотреть отдельно, не связывая ее с нахождением ПРВ длительности выбросов. Рассмотрение проводится для двух случаев: когда извест­но совместное распределение случайного процесса и его производ­ной, и когда известна только двумерная ФРВ случайного процесса.

20.3.1. Определение характеристик выбросов

с использованием совместного распределения случайного процесса и его производной

Рассмотрим стационарный случайный процесс ξ(t) на интерва­ле времени [t, t + T]. Разобьем интервал T на n участков длитель­ностью ∆t=T/n. Обозначим вероятность пересечения случайным процессом уровня х снизу вверх (с положительным значением про­изводной) каждого участка р . Среднее значение числа пересече­ний случайным процессом уровня х на всем интервале Т равно nр.

Средняя частота пересечений уровня х случайным процессом сни­зу вверх оценивается выражением

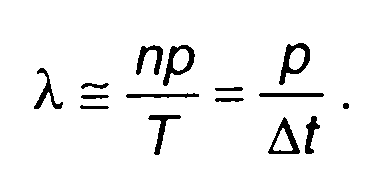(20.80)

Чем меньше значение ∆t, тем точнее записанное выражение. Точное значение λ. получим при ∆t→0

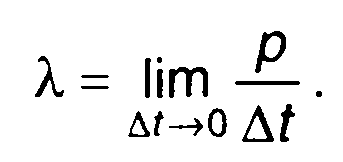(20.81)

Величина р определяется вероятностью одновременного вы­полнения следующих неравенств:

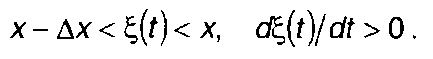(20.82)

Если f_ξη(х,у) - двумерная ПРВ случайного процесса ξ(t) и его производной η(t)= dξ(t)/dt в момент времени t, то вероятность вы-

полнения неравенств (20.82) определяется как

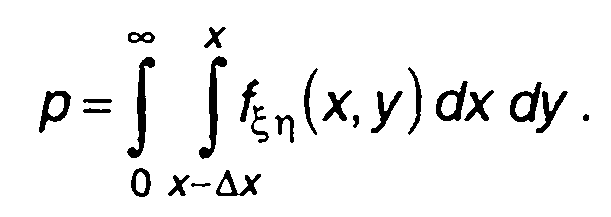(20.83)

При достаточно малом значении ∆x внутренний интеграл в (20.83) можно представить в виде

где 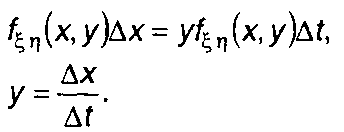(20.84)

С учетом (20.84) выражение (20.83) примет вид

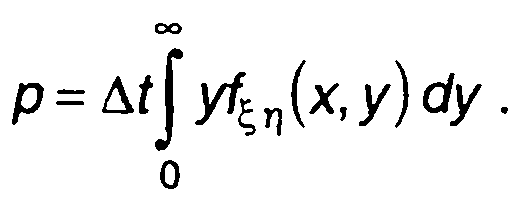(20.85)

Из (20.81) с учетом (20.85) получим

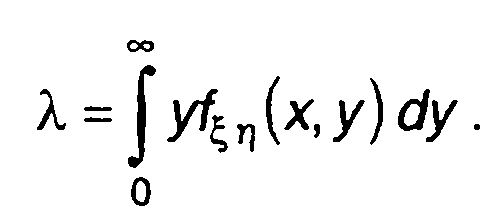(20.86)

Таким образом, зная совместную ПРВ случайного процесса и его производной для одного и того же момента времени, можно оп­ределить среднюю частоту следования нулей случайного процесса (при пересечении уровня снизу вверх). Эта частота совпадает со средней частотой положительных выбросов случайного процесса.

Аналогично получается выражение для средней частоты нулей случайного процесса при пересечении им уровня х сверху вниз. Оно совпадает с (20.86). Этим же выражением определяется и средняя частота следования отрицательных выбросов.

Используя λ, можно определить среднюю длительность выбро­сов относительно заданного уровня.

Для эргодических случайных процессов среднее время непре­вышения уровня х на интервале времени Т может быть определе­но как TF₁(х), где F₁(х) - ФРВ случайного процесса. Среднее число выбросов на интервале времени T равно λ T.

Таким образом, средняя длительность отрицательных выбросов равна

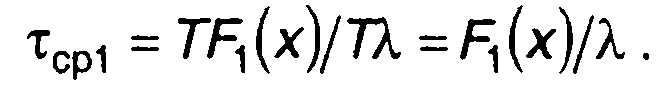(20.87)

Средняя длительность положительных импульсов определяется аналогично

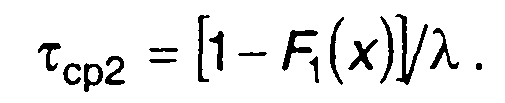(20.88)

Конкретизируем полученные результаты для гауссовского про­цесса. Совместная ПРВ центрированного гауссовского процесса и его производной в один и тот же момент времени описывается вы­ражением (разд. 16)

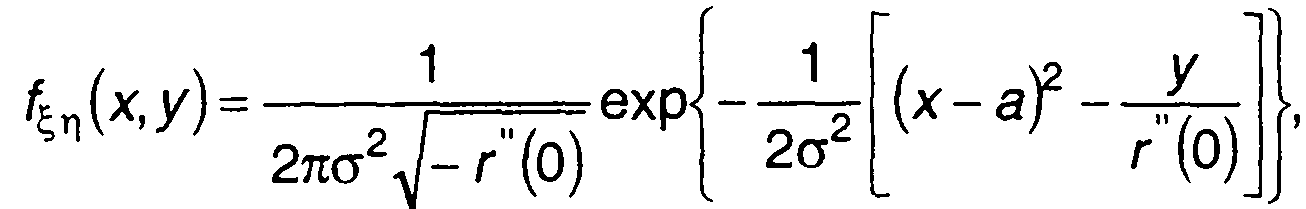(20.89)

где а, σ2, r(т) - математическое ожидание, дисперсия и нормиро­ванная корреляционная функция случайного процесса.

Подставляя (20.89) в (20.86), для средней частоты следования выбросов гауссовского процесса получим следующее выражение

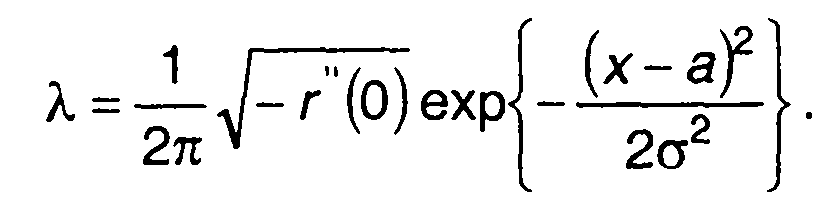(20.90)

При х = а

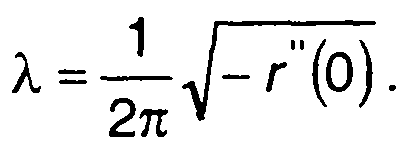(20.91)

Используя спектральную плотность мощности случайного про­цесса N(ω), запишем

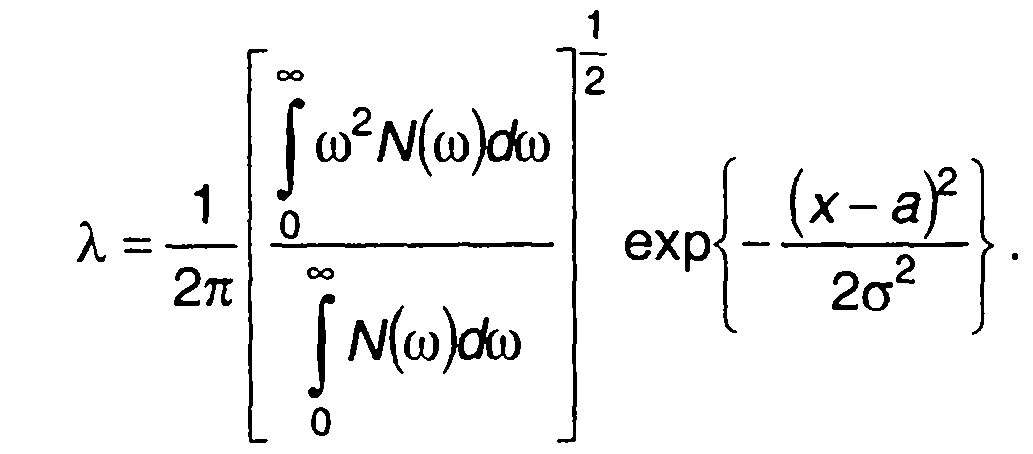(20.92)

При х = а

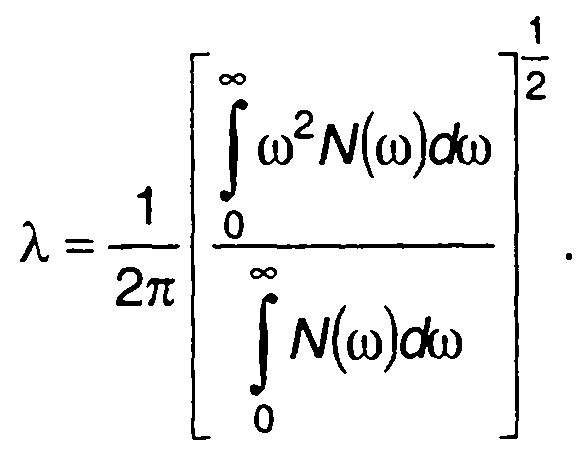(20.93)

Средняя длительность отрицательных выбросов гауссовского процесса с учетом (20.90) определяется выражением

где 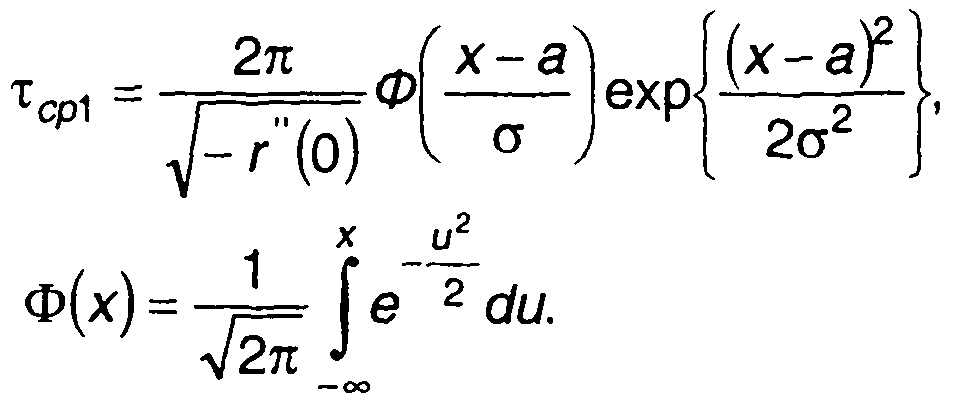(20.94)

Средняя длительность положительных выбросов

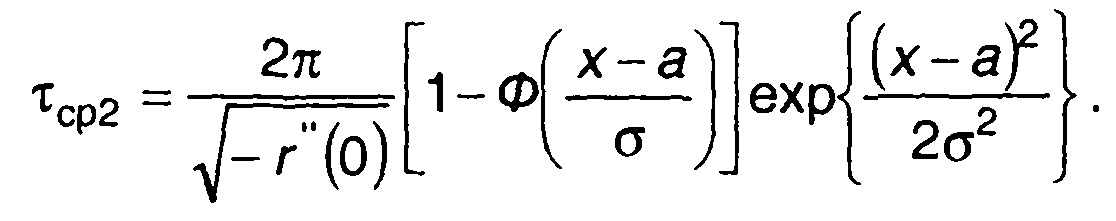(20.95)

При х = а

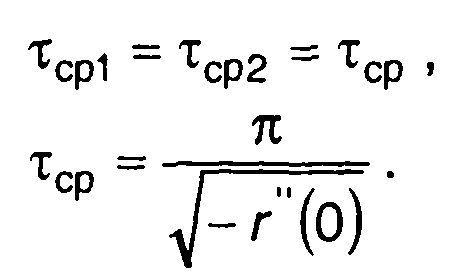(20.96)

Таким образом, определены средняя частота следования вы­бросов и средняя длительность выбросов с использованием со­вместной ПРВ случайного процесса и его производной. Получен­ные выражения совпадают с соответствующими выражениями, приведенными в п. 20.1 и п. 20.2.2.

Средняя частота следования выбросов и средняя длительность выбросов могут быть также определены с использованием только двумерной ПРВ случайного процесса.

20.3.2. Определение характеристик выбросов с использованием двумерной ПРВ случайного процесса

Как было установлено, средняя частота пересечений случай­ным процессом заданного уровня снизу вверх определяется сле­дующим предельным соотношением

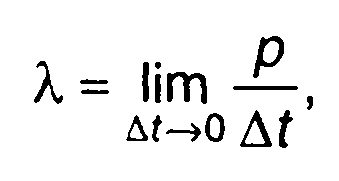(20.97)

где р - вероятность пересечения случайным процессом уровня х снизу вверх интервала длительностью ∆t.

Вероятность хотя бы одного пересечения случайным процессом уровня х снизу вверх на интервале времени [t, t + ∆t] можем опре­делить как

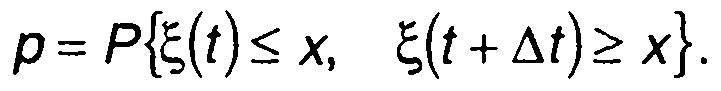(20.98)

Используя двумерную ПРВ случайного процесса ξ(t) для мо­ментов времени t и t + ∆t, выражение для р запишем в виде

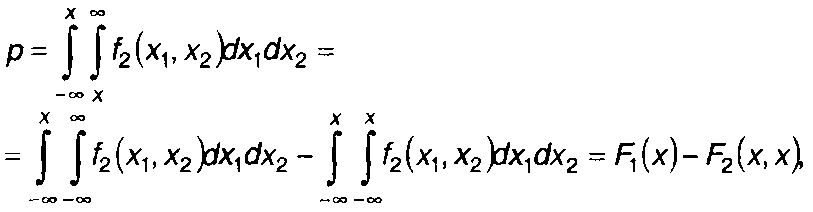(20.99)

где f2(x₁,x₂), F₁(x₁), F₂(x₁,x₂) - ПРВ и ФРВ случайного процесса.

С учетом (20.97) выражение для средней частоты следования выбросов случайного процесса примет вид

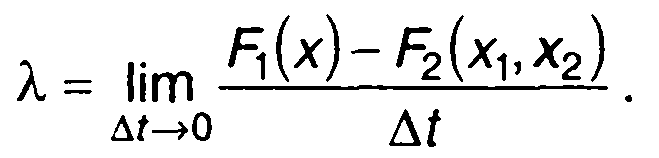(20.100)

Таким образом, имея двумерную ФРВ случайного процесса, можно определить среднюю частоту следования его выбросов.

Для гауссовского процесса, воспользовавшись соотношениями, полученными в разд. 16, найдем

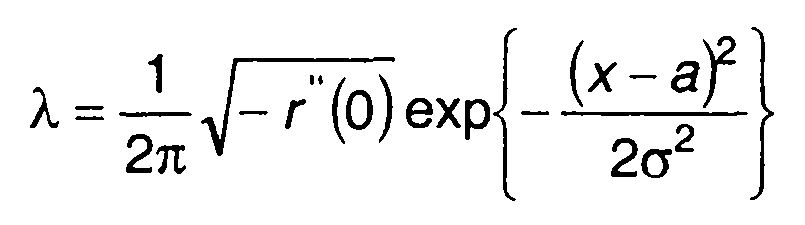(20.101)

что совпадает с (20.90).

Аналогично можно получить выражения для других средних ха­рактеристик случайного процесса: средней частоты пересечений случайным процессом заданного уровня сверху вниз, средней час­тоты следования выбросов, средней длительности отрицательных и положительных выбросов.

Как следует из сопоставления результатов, оба подхода (с ис­пользованием совместной ПРВ случайного процесса и его произ­водной и с использованием двумерной ПРВ случайного процесса) дают идентичные выражения. Они совпадают и с результатами, полученными на основе решения для ПРВ длительности выбросов, приведенными в п. 20 1.

20.4. Средняя частота следования экстремумов случайного процесса

Подходы к определению характеристик выбросов, изложенные в § 20.3, позволяют найти и среднюю частоту следования макси­мумов случайного процесса. Определим ее, используя двумерную ПРВ случайного процесса.

Рассмотрим стационарный случайный процесс ξ(t) на интерва­ле времени [t, t + T]. Интервал Т разобьем на л участков длитель­ностью ∆t-T/n. Средняя частота следования максимумов слу­чайного процесса определяется выражением, аналогичным (20.97)

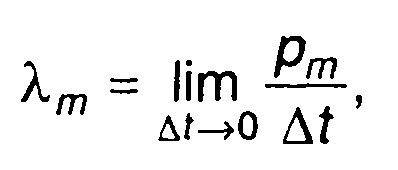(20.102)

где р_т - вероятность появления максимума случайного процесса

на интервале времени ∆t.

Вероятность того, что случайный процесс имеет хотя бы один максимум на интервале ∆t, определяется выражением

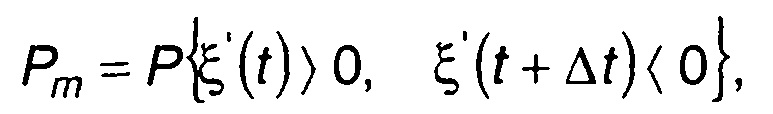(20.103)

если существует производная случайного процесса ξ(t). Зная дву­мерную ПРВ производной случайного процесса, для вероятности (20.103) запишем

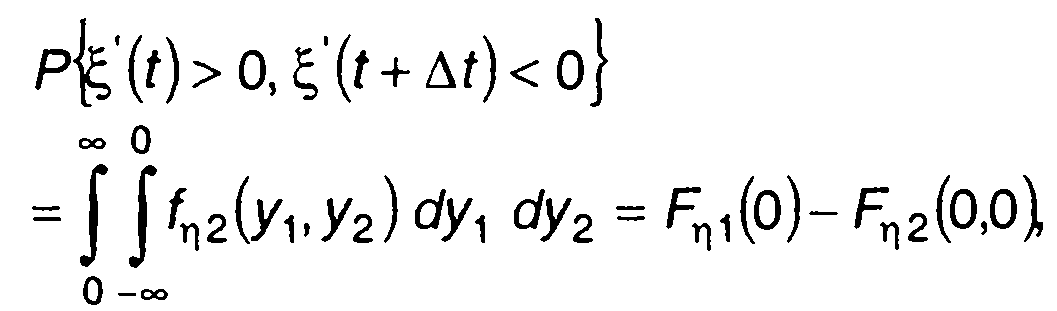(20.104)

где. f_η2(y,y), F_η1(y), F_η2(y,y) - ПРВ и ФРВ производной случайного процесса η(t) = ξ`(t).