ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 27 страница

23.4.1. Оценка корреляционной функции случайного про­цесса при ограниченном времени наблюдения

При наблюдении случайного процесса на выходе перемножите­ля в течение времени t_k оценкой корреляционной функции центри­рованного процесса ξ(t) будет величина

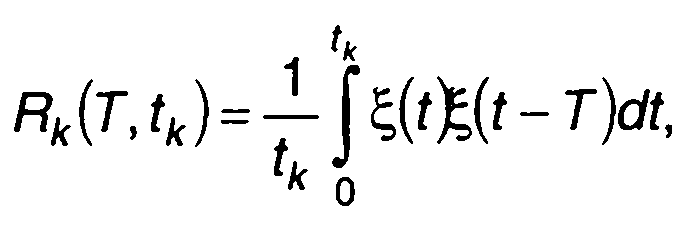(23.30)

где Т- смещение во времени на одном из входов перемножителя. Математическое ожидание R_k(T,t_k) равно

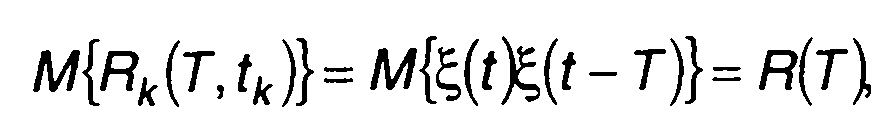(23.31)

где R(т) - корреляционная функция случайного процесса ξ(t). Результат усреднения (23.31) показывает, что R_k(T,t_k) являет­ся несмещенной оценкой корреляционной функции ξ(t). Поэтому ошибку определения корреляционной функции по (23.30) можно оценивать, оперируя только средним квадратическим отклонением R_k(T,t_k)

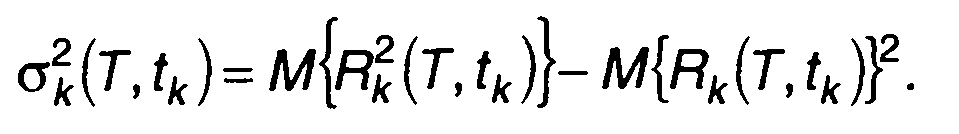(23.32)

Первое слагаемое в (23.32) определяется выражением

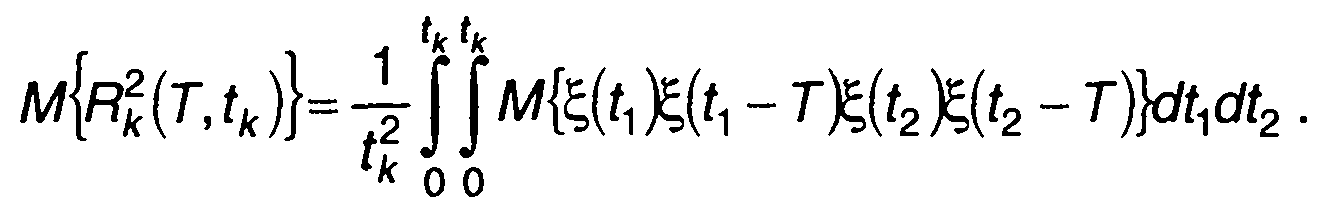(23.33)

Подставляя (23.31) и (23.33) в (23.32), запишем

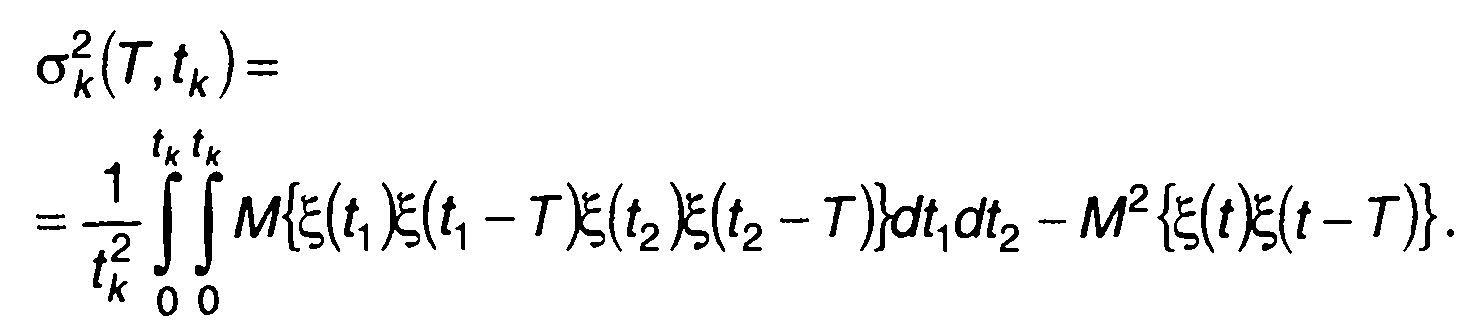(23.34)

Для гауссовского процесса 4(0 подынтегральное выражение в (23.34) можем записать в виде

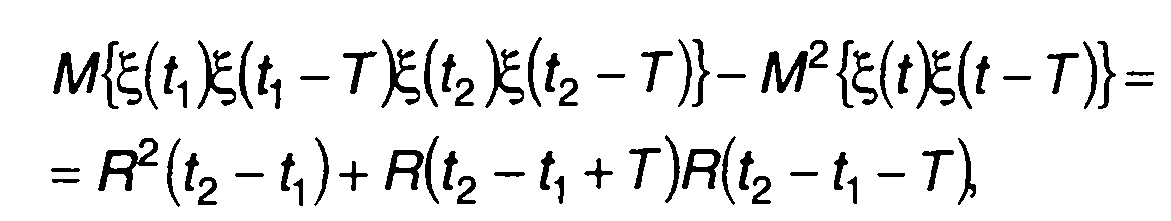(23.35)

где R(т) - корреляционная функция ξ(t).

Подставив (23.35) в (23.34), получим

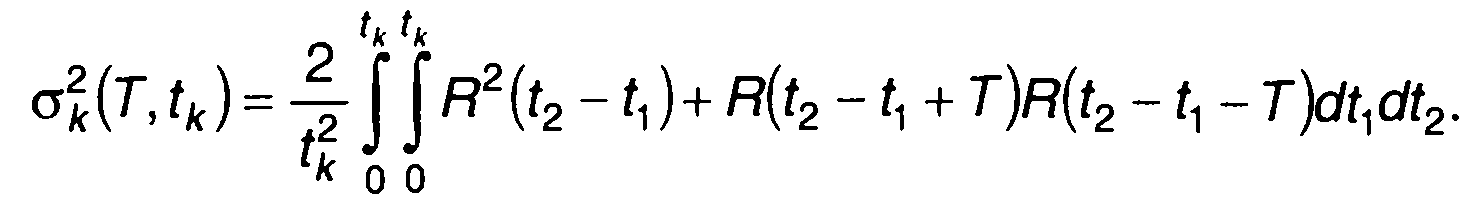(23.36)

Производя замену переменных, как это было сделано в § 23.3, получим

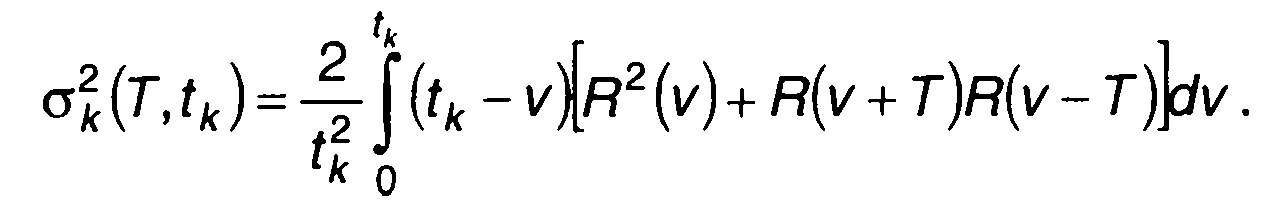(23.37)

Выражение (23.37) дает зависимость дисперсии от времени на­блюдения t_k при заданной корреляционной функции случайного процесса.

Относительная ошибка определения корреляционной функции равна

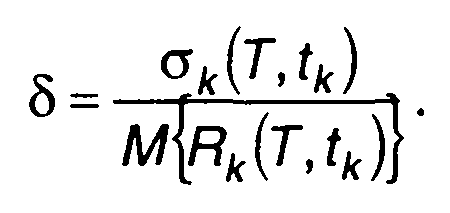(23.38)

Подставив в (23.38) выражение для σ_k(T,t_k) и R_k(T,t_k), запи­шем

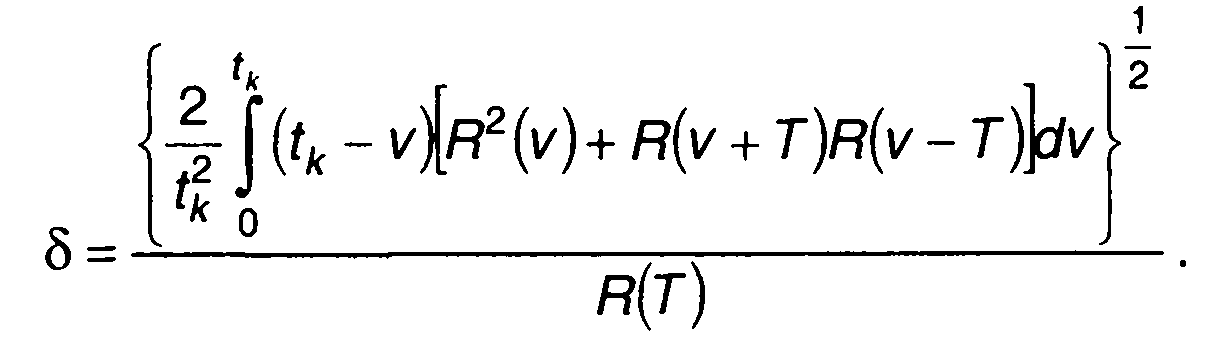(23.39)

В качестве призера рассмотрим случайный процесс, имеющий корреляционную функцию вида

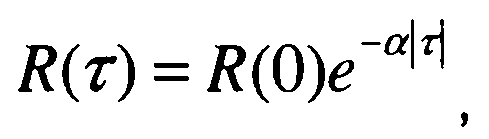
где а - постоянная величина.

Подставив выражение для корреляционной функции в (23.39), получим

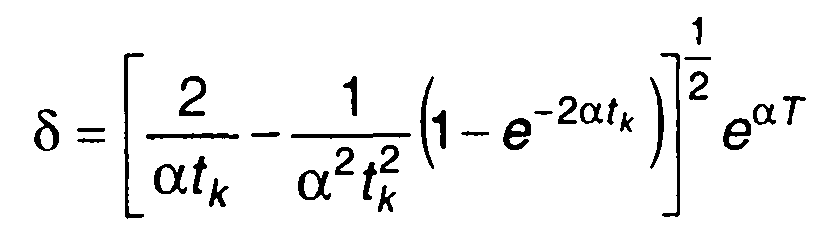
или

где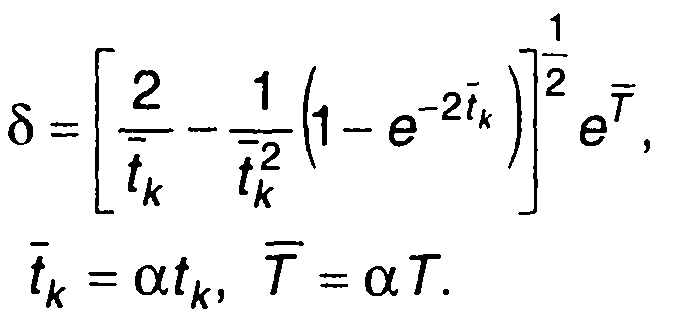

Как следует из записанных выражений, ошибка зависит от: кор­реляционной функции случайного процесса, R(т); задержки слу­чайного процесса на входе, Т; времени наблюдения, t_k.

Для условий примера - ошибка определяется параметрами а, T и t_k.

При T=0 (рис. 23.6)

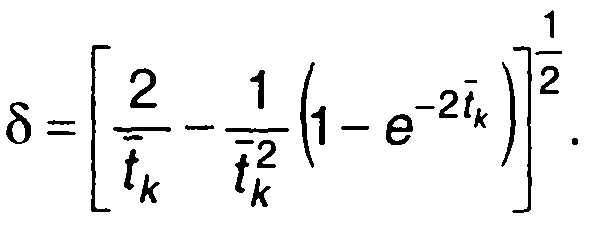
При достаточно большом значении t_k можно пользоваться сле­дующим приближенным равенством

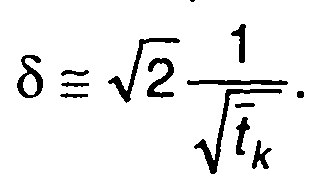
Принимая интервал корреляции τ_к = 3/ a, (R(τ_k)≤ 0,05R(0)), последнее выражение для δ можем записать в виде

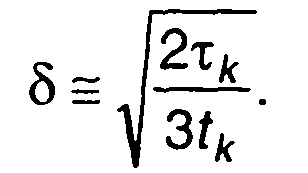
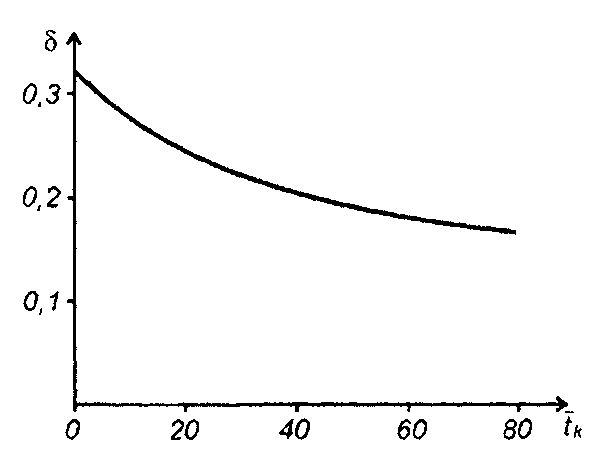
Рис. 23.6

Время наблюдения практически не влияет на определение кор­реляционной функции случайного процесса при значении t_k > 300τ_к. При выполнении этого неравенства ошибка определе­ния корреляционной функции составит менее 5%.

23.4.2. Аппаратурное определение корреляционной функции случайного процесса за ограниченное время

При определении корреляционной функции случайного процес­са за ограниченное время t_k случайный процесс на выходе корре­лятора описывается выражением

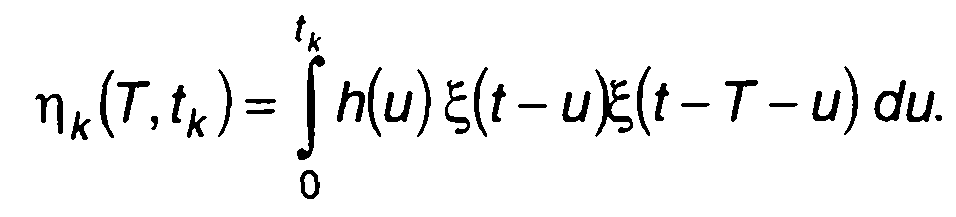(23.40)

Моменты первого и второго порядков η_k(T,t_k) равны

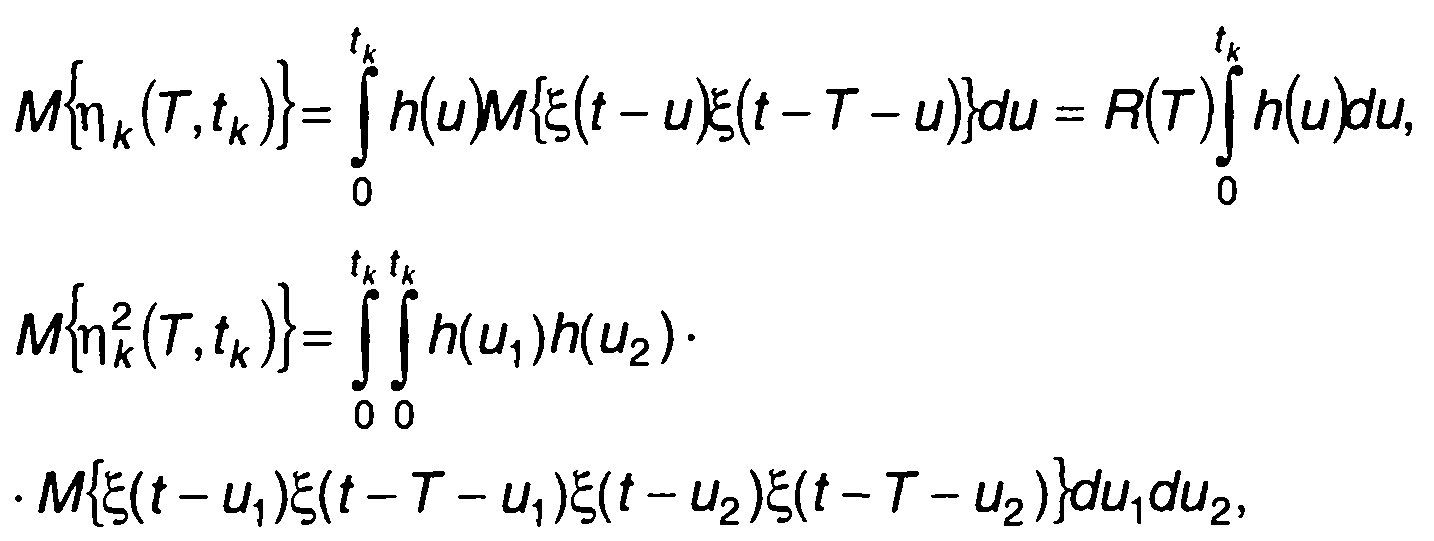(23.41)

где R(т) - корреляционная функция случайного процесса ξ(t) Дисперсия случайного процесса η_k[T,t_k) определяется как

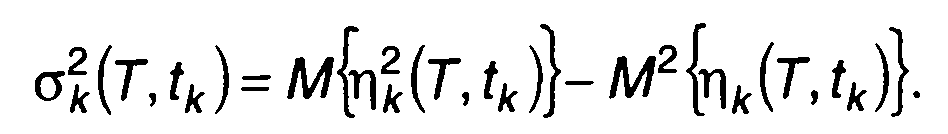(23.42)

Подставляя (23.41) в (23.42) и используя представление момен­та четвертого порядка гауссовского процесса с помощью моментов второго порядка, получим

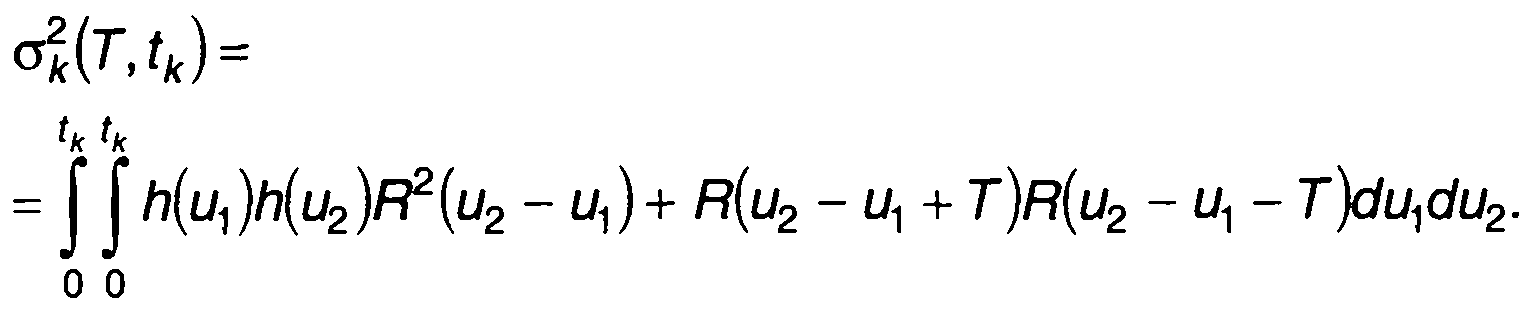(23.43)

Произведя замену переменных в (23.43), выражение для σ_k²(T,t_k) запишем в виде

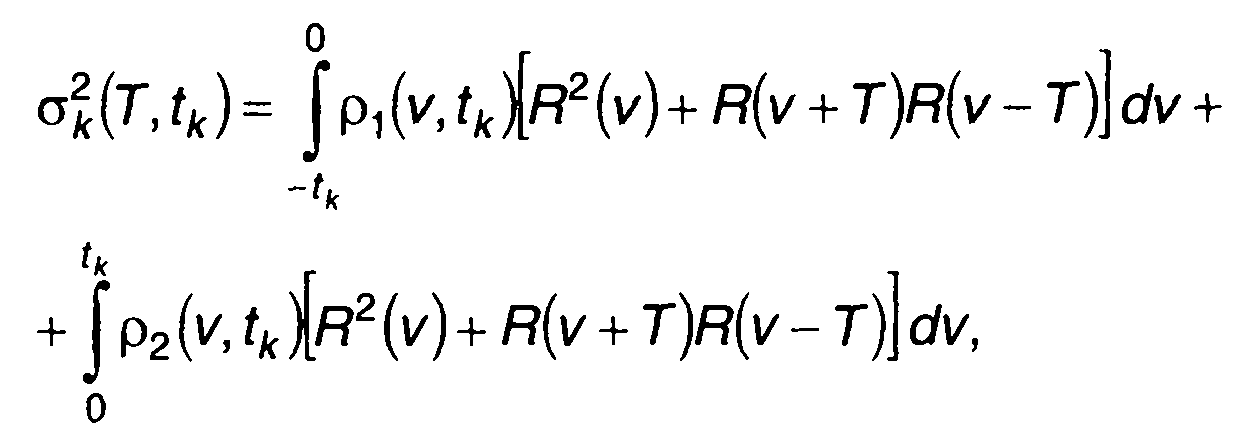(23.44)

где

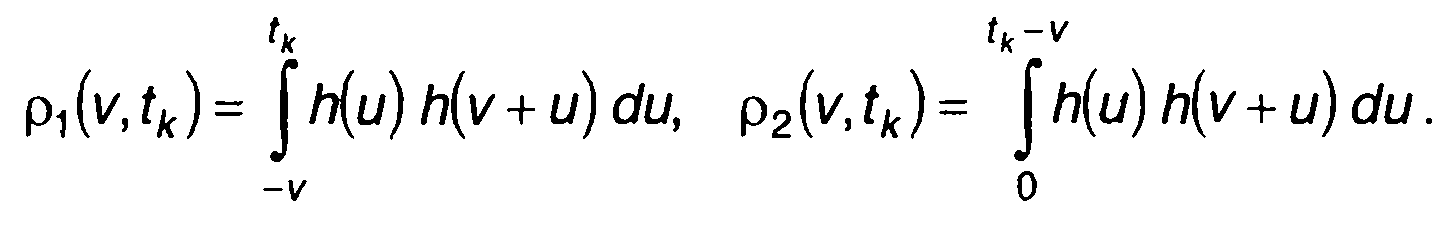(23.45)

Относительная ошибка оценки корреляционной функции опре­деляется выражением

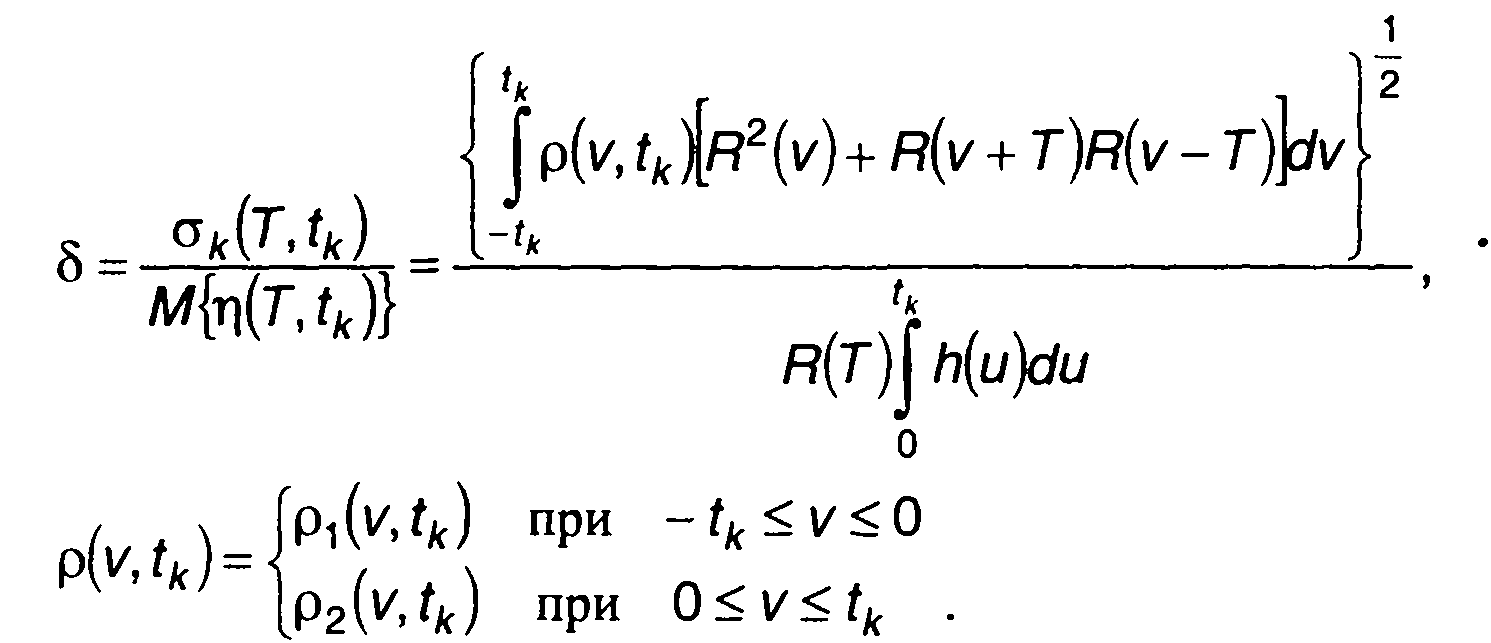(23.46)

Ошибка зависит от времени измерения корреляционной функ­ции, вида корреляционной функции, вида и параметров фильтра коррелятора.

При T = 0

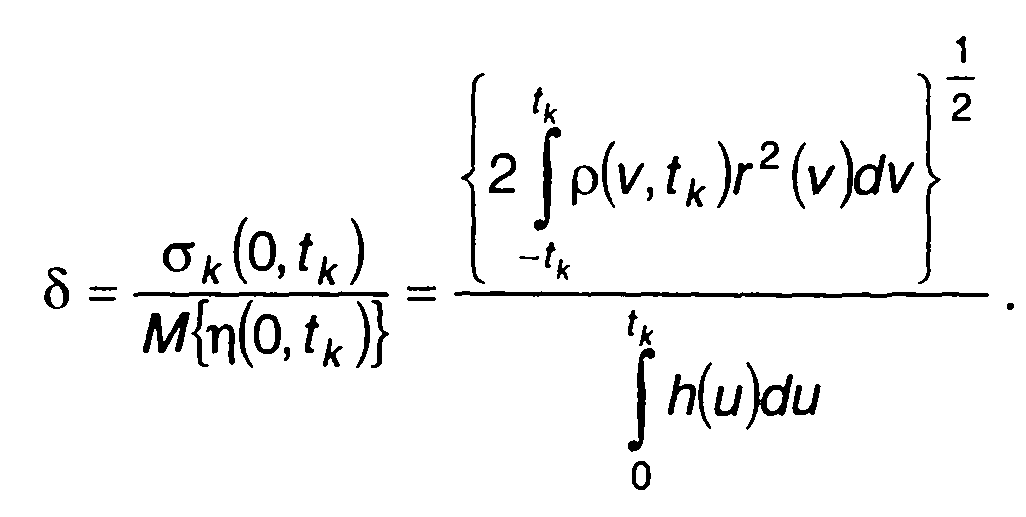(23.47)

Для RC - фильтра с импульсной характеристикой h(t) = bе^-bt , и корреляционной функцией экспоненциального вида

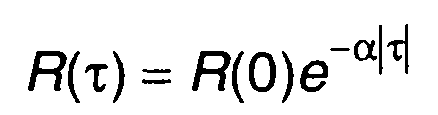
из (23.47) получим

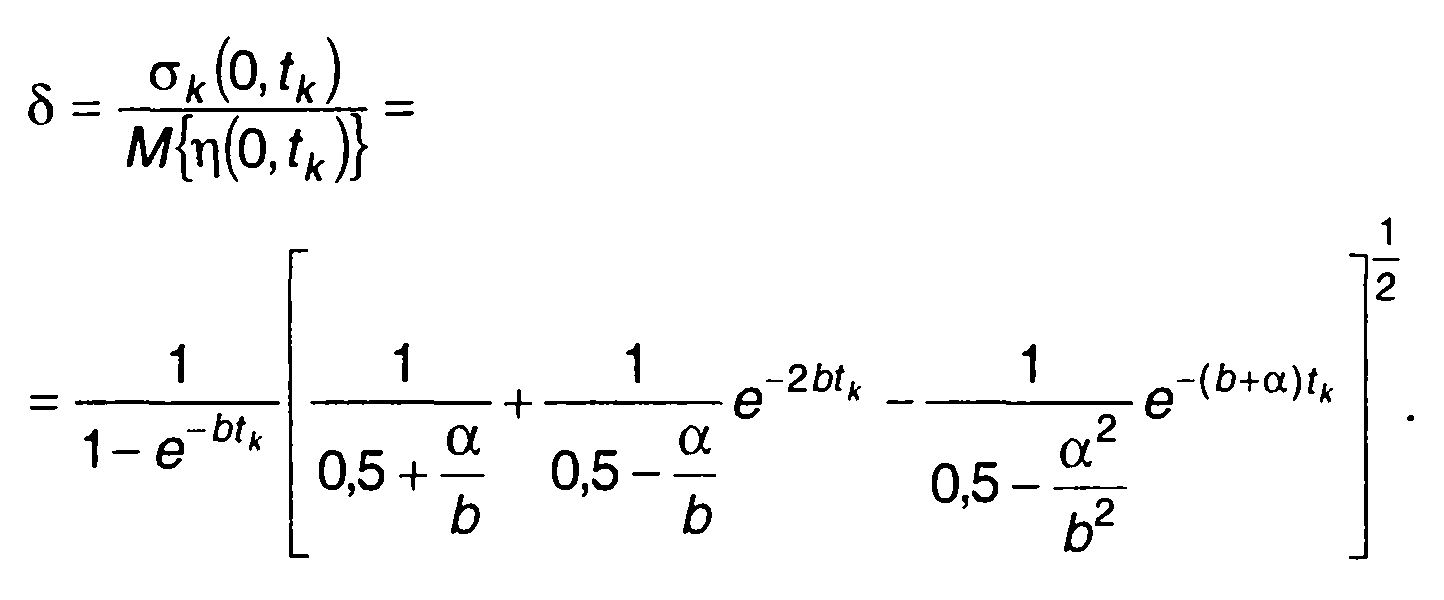
При t_k→∞ имеем

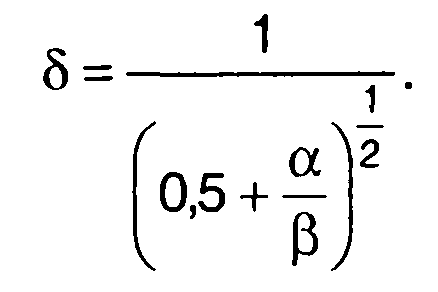
Сравнение выражений для относительной ошибки при ограни­ченном времени измерения и неограниченно большом показывает, что для условий примера при t_k>T = (1 / b) влиянием времени из­мерения на ошибку можно пренебречь, ошибка составляет доли процента.

23.5. Характеристики сигнала на выходе корреляционного транспонатора

Оценкой корреляционной функции случайного процесса являет­ся постоянная составляющая на выходе коррелятора при фиксиро­ванном значении задержки на входе. Изменение во времени за­держки на входе позволяет наблюдать корреляционную функцию в заданном интервале значений задержки (рис. 23.7). Если задержка т изменяется во времени с постоянной скоростью

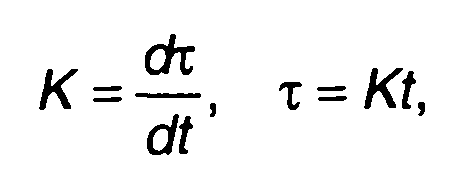(23.48)

то, не учитывая возможные ошибки, сигнал на выходе коррелятора при некоторых условиях (определенных в дальнейшем) можно представить в виде (постоянный коэффициент принят равным еди­нице)

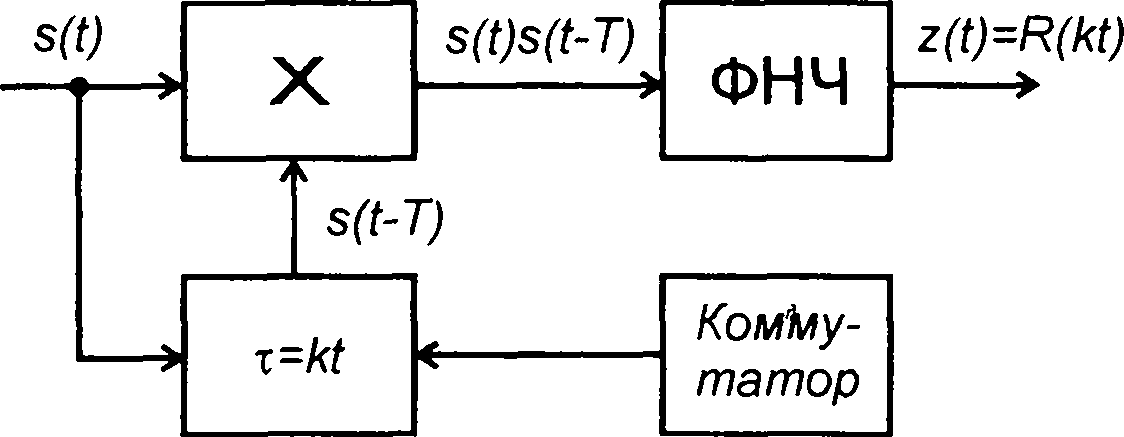
Рис.23.7

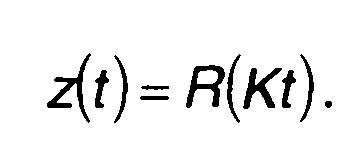(23.49)

Спектральную плотность этого сигнала определим преобразо­ванием Фурье

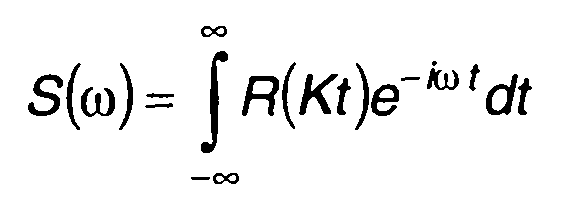(23.50)

С учетом (23.48) можно записать

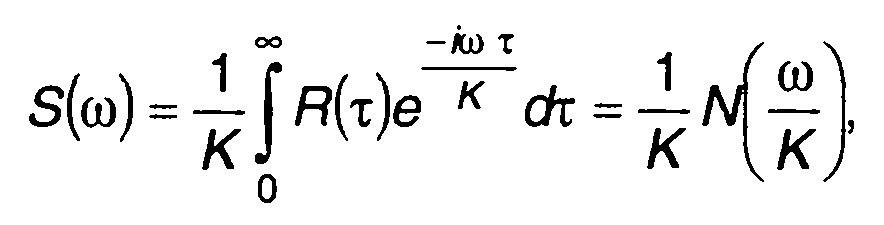(23.51)

где N(ω) - спектральная плотность мощности случайного процесса на входе

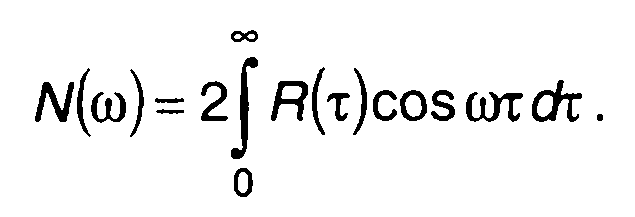(23.52)

Сравнение (23.51) и (23.52) показывает, что спектр сигнала на выходе коррелятора при изменении задержки во времени повторя­ет по форме спектральную плотность мощности случайного про­цесса на входе; происходит изменение масштаба по оси частот: изменяется положение спектра на оси частот и его ширина (рис. 23.8). Этот результат вытекает непосредственно из свойств преобразования Фурье.

Однако сделанные выводы справедливы при условии, что сиг­нал на выходе коррелятора соответствует корреляционной функ­ции. При аппаратурной реализации условия, выполняемые на практике, отличаются от принятых.

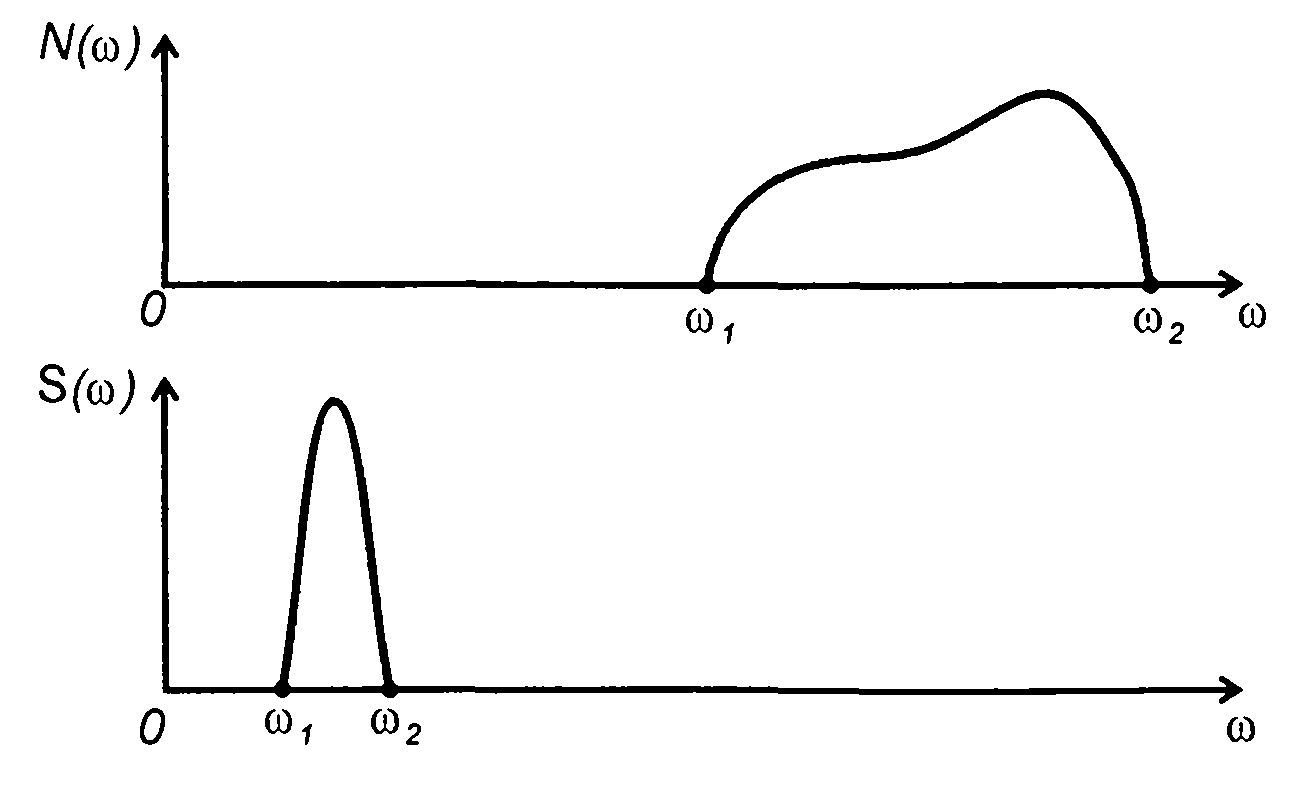
Рис. 23.8

Сигнал оценки корреляционной функции при постоянном значе­нии задержки на входе представляет постоянную составляющую на выходе перемножителя. При изменении задержки во времени этот сигнал на выходе безинерционного перемножителя изменяет­ся в соответствии с изменением корреляционной функции R(Kt).

При прохождении сигнала через фильтр коррелятора возникают искажения, которые приводят к изменению сигнала на выходе. Ес­ли изменение задержки во времени происходит после того, как сиг­нал на выходе фильтра принял установившееся значение R(0), то в момент времени t (соответствующий задержке т = Kt) сигнал бу­дет описываться выражением

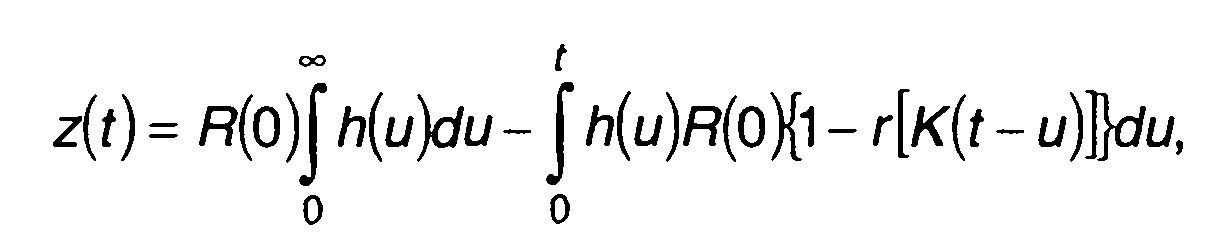(23.53)

где h(t) - импульсная характеристика фильтра.

Сигнал, описываемый (23.53), только приближенно соответству­ет корреляционной функции (рис. 23.9). Степень соответствия оп­ределяется соотношением параметров корреляционной функции, фильтра и скорости изменения задержки во времени. Степень со­ответствия (23.53) и (23.49) можно оценить относительным значе­нием разности

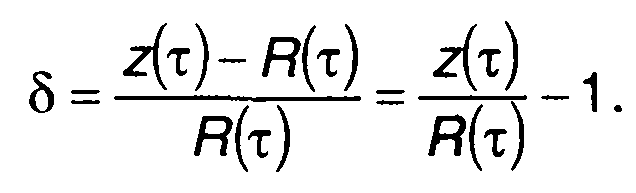(23.54)

Так для RC -фильтра

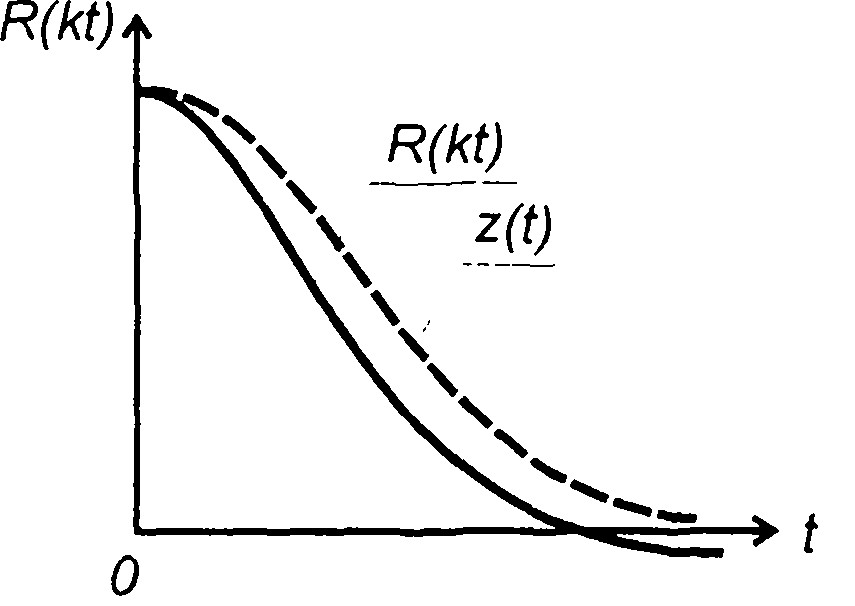
Рис. 23.9

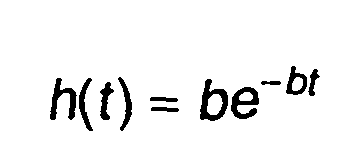
и корреляционной функции экспоненциального вида

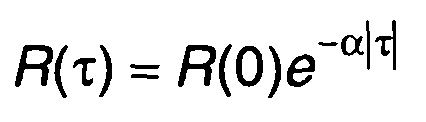
из (23.53) получим

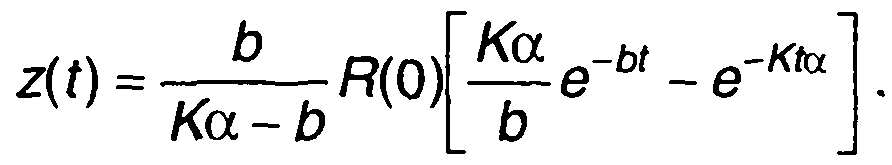
Переходя к т, запишем

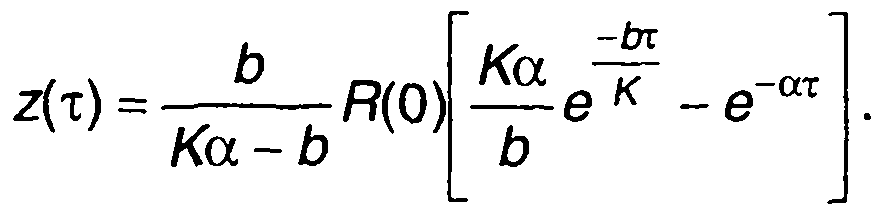
Ошибка определения корреляционной функции найдется из (23.54), рис. 23.10.

Как следует из записанного выражения и приведенных графи­ков, ошибка зависит от:

Ка - крутизны корреляционной функции и скорости изменения задержки во времени;

b/Ка - соотношения между крутизной корреляционной функ­ции, скоростью изменения задержки и постоянной фильтра; т - значения задержки, для которого ведется рассмотрение. Ошибка, сопровождающая транспонирование спектра, может быть определена как

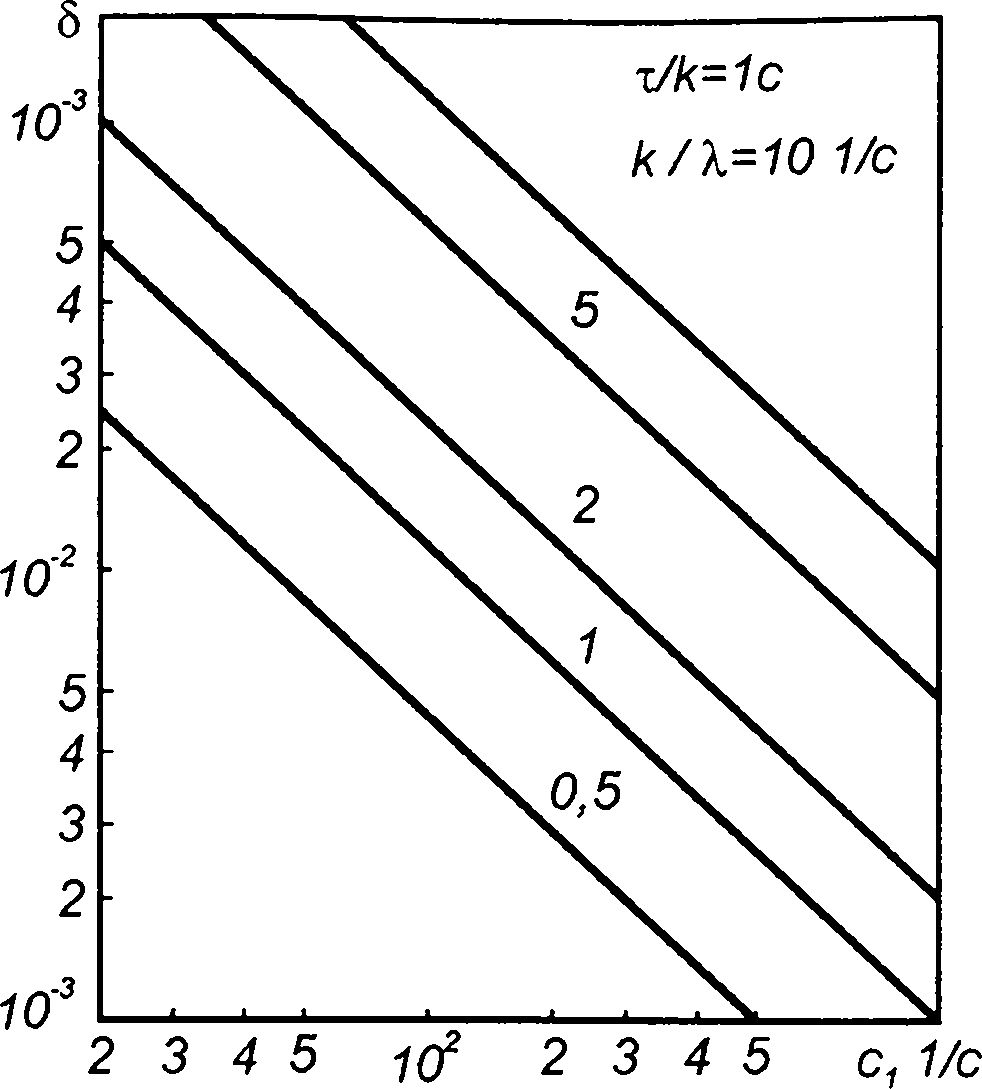
Рис. 23.10

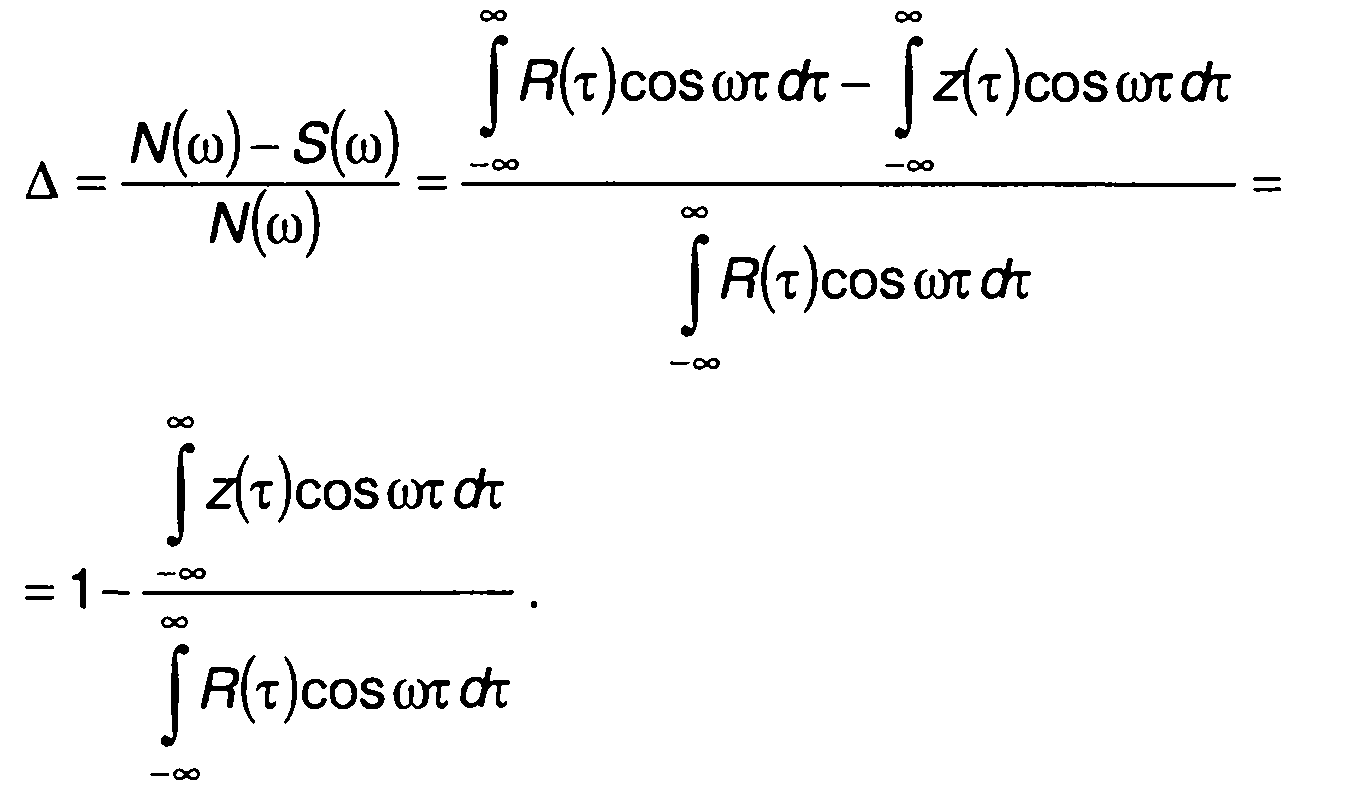(23.55)

Для условий рассмотренного примера получим

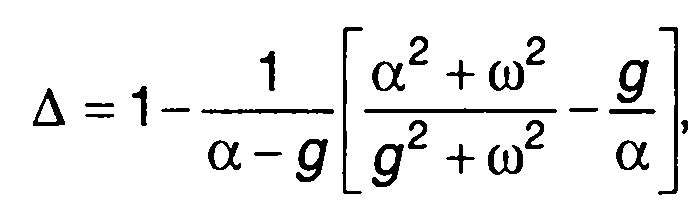
где g = b/К = 1/ТК; Т- постоянная времени фильтра.

Ошибка зависит от тех же параметров, которые влияют на точ­ность определения корреляционной функции. При заданном виде корреляционной функции ошибка определяется соотношением

между скоростью изменения задержки и постоянной времени фильтра. Для каждой корреляционной функции можно установить такую скорость изменения задержки и выбрать параметры фильтра таким образом, что ошибка, возникающая при транспонировании спектра не будет превышать допустимого значения.

Если на вход перемножителя подается гармоническое колеба­ние

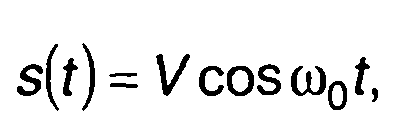(23.56)

то при постоянной задержке τ на выходе выделяется постоянная составляющая, соответствующая корреляционной функции

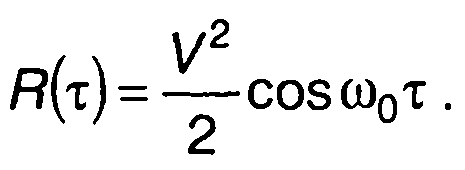(23.57)

При изменении задержки во времени с постоянной скоростью на выходе фильтра выделяется сигнал (по аналогии с (23.49))

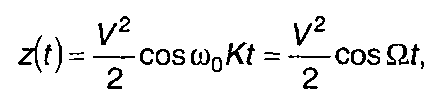(23.58)

где К - скорость изменения задержки во времени, Ω = Кω₀.

Таким образом, коррелятор с переменной задержкой на одном из входов выполняет функции преобразователя частоты. При К = 10^-3 на выходе выделяется также гармоническое колебание с частотой на три порядка меньше частоты колебания на входе (рис. 23.11). На рисунке изображены спектральная плотность сигнала на входе S₁(ω) и выходе S₂(ω) преобразователя.

Наряду со схемной простотой корреляционный преобразова­тель частоты обеспечивает помехоустойчивость системы. Если на коррелятор помимо гармонического колебания воздействует шум, корреляционная функция которого R_n(т) = R_n(0)г_n(т), то при изме­нении во времени задержки (t = Kt) на выходе преобразователя

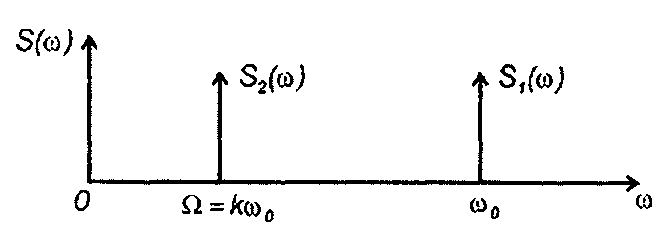
Рис. 23.11

выделяется непериодическое колебание z_n(t) = R_n(0)r_n(Kt). При достаточно большом значении т (или t) значение z_n(t) может быть получено достаточно малым (рис. 23.12).

Помимо постоянной составляющей (при переменной задержке т - медленно меняющаяся во времени составляющая) на выходе коррелятора присутствуют флуктуации (рис. 23.12). При нормаль­ном распределении шума корреляционная функция флуктуаций на выходе перемножителя определяется выражением (23.10)

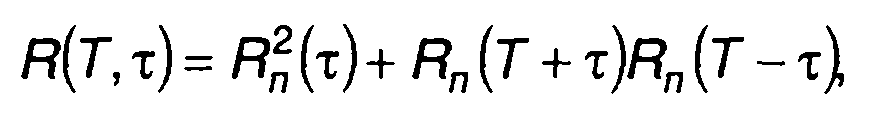(23.59)

где R_n(т) - корреляционная функция шума на входе.

При достаточно большом значении Т имеем

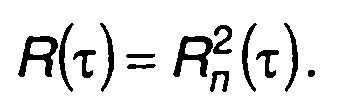(23.60)

Спектральная плотность мощности флуктуаций на выходе пе­ремножителя определится выражением

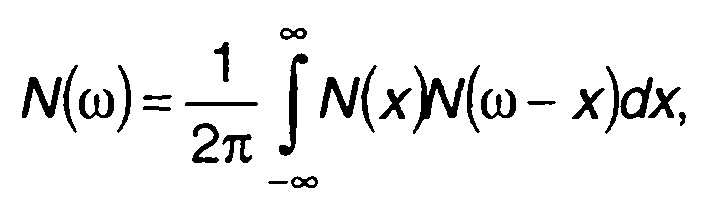(23.61)

где N(ω) - спектральная плотность шума на входе.

Спектральная плотность мощности колебания на выходе фильтра

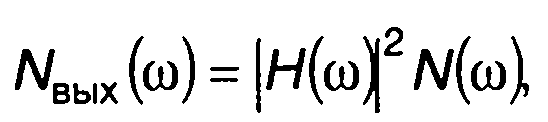(23.62)

Дисперсия колебания на выходе фильтра описывается выраже­нием

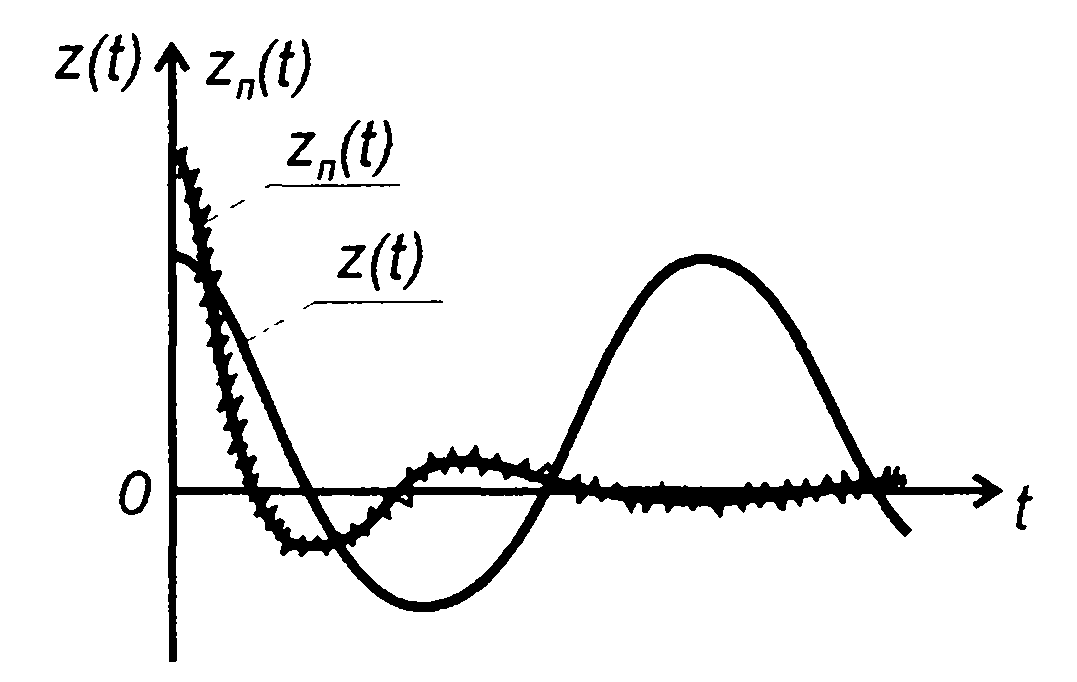
Рис. 23.12

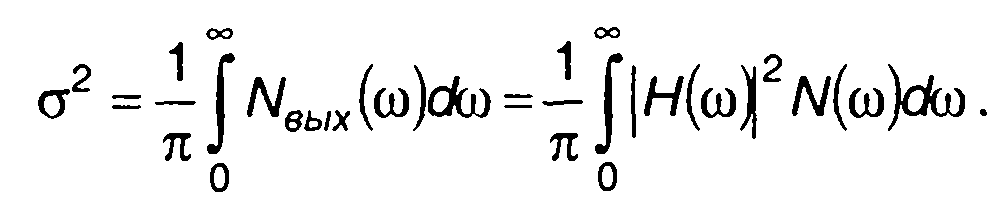(23.63)

Для узкополосного фильтра

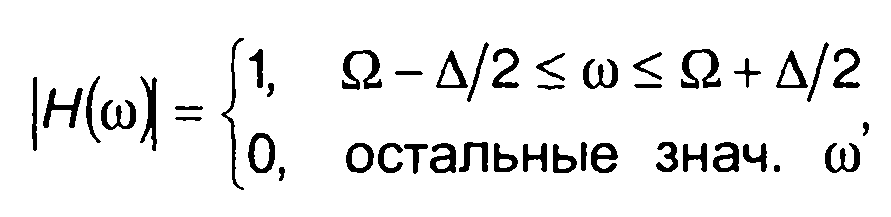(23.64)

из (23.63) получим

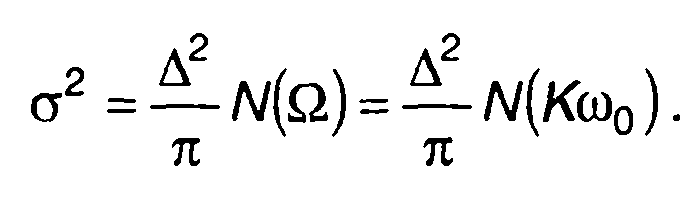(23.65)

Как следует из (23.65), σ² зависит от спектральной плотности мощности шума (на выходе перемножителя) в полосе пропускания фильтра и ширины полосы пропускания фильтра. Сужая полосу пропускания фильтра, можно добиться снижения уровня флуктуа­ций шума на выходе. Ограничения, накладываемые на выбор по­лосы пропускания, обусловлены ее влиянием на передачу гармо­нического колебания.