ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 25 страница

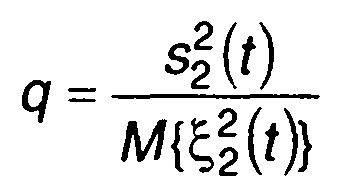(21.40)

было бы максимальным.

Сигнал на выходе цепи определяется выражением

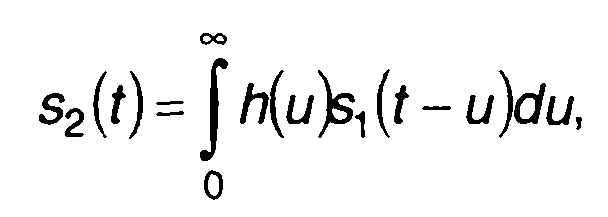(21.41)

где h(t) - импульсная характеристика цепи.

Шум на входе цепи чаще всего можно рассматривать как белый. На практике это означает, что ширина полосы частот, занимаемая шумом, значительно больше ширины полосы пропускания цепи. Дисперсия шума на выходе цепи при подаче на вход белого шума описывается выражением (21.21). Учитывая, что корреляционная функция белого шума равна R(т) = N₀δ(т), получим

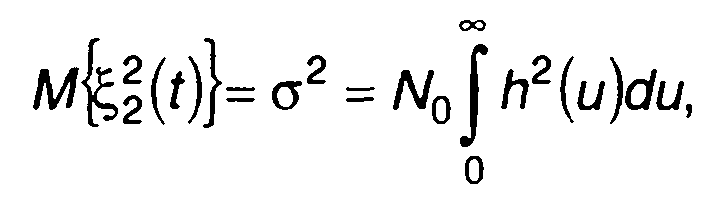(21.42)

где N₀- спектральная плотность мощности белого шума на входе цепи.

Отношение сигнал/шум на выходе цепи в момент времени t₀ определим с учетом (21.41) и (21.42)

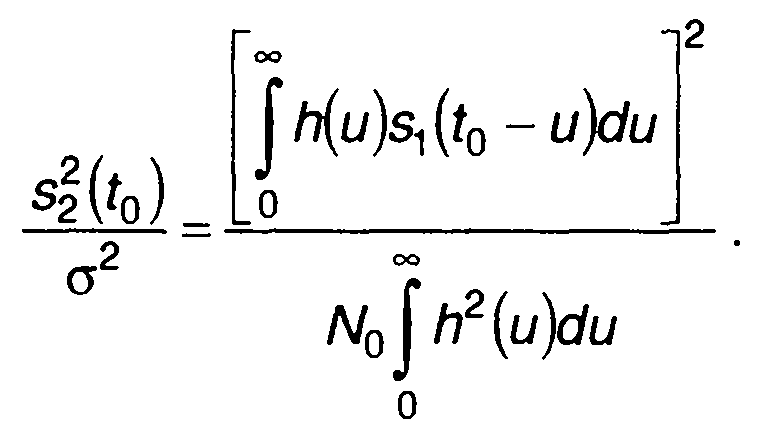(21.43)

Найдем такую импульсную характеристику цепи, которая обес­печивала бы максимальное отношение сигнал/шум (21.43). Для этого обратимся к неравенству Буняковского-Шварца

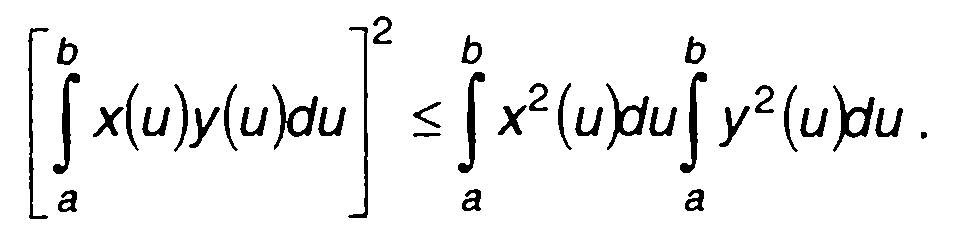(21.44)

Равенство в (21.44) имеет место при х(и) = kу(и), где k - посто­янная величина. С учетом (21.44) выражение (21.43) запишем в виде неравенства

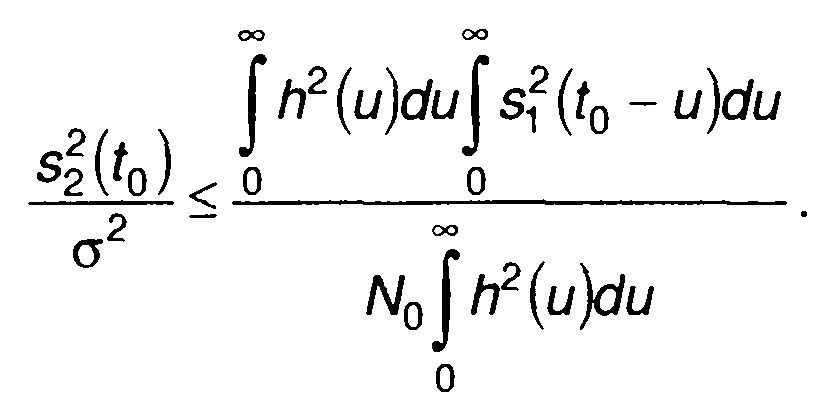(21.45)

Анализ (21.45) показывает, что максимум отношения сиг­нал/шум получается когда выполняется равенство

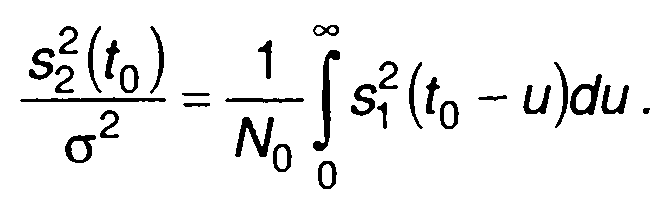(21.46)

Равенство выполняется при условии

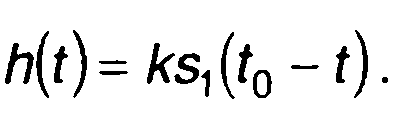(21.47)

Постоянная величина k не влияет на вид импульсной характе­ристики и ее можно не рассматривать, т.е. полагать

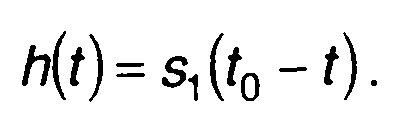(21.48)

Таким образом, максимум отношения сигнал/шум обеспечива­ется линейной цепью, имеющей импульсную характеристику, опре­деляемую видом сигнала. Цепь, имеющая импульсную характери­стику, описываемую (21.48) называется согласованной цепью или согласованным фильтром. Как следует из (21.48), импульсная ха­рактеристика такой цепи с точностью до постоянной величины яв­ляется зеркальным отражением сигнала, сдвинутым на t₀ по оси времени.

Если сигнал s₁(t) имеет спектральную плотность S₁(ω), то сме­щению во времени на t₀ соответствует умножение на множитель

задержки е^-iωt0

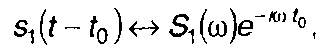(21.49)

где знак ↔ означает соответствие по Фурье.

Величине s,(t₀-t) соответствует комплексно-сопряженная ве­личина S₁* (ω)e^iωt0. Следовательно, частотная характеристика со­гласованного фильтра, обеспечивающего максимум отношения сигнал/шум, описывается выражением

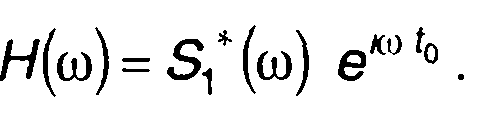(21.50)

В качестве примера приведем характеристики фильтра, согла­сованного с прямоугольным импульсом. Импульсная характеристи­ка цепи, максимизирующей отношение сигнал/шум в момент вре­мени t₀ = т_u имеет вид

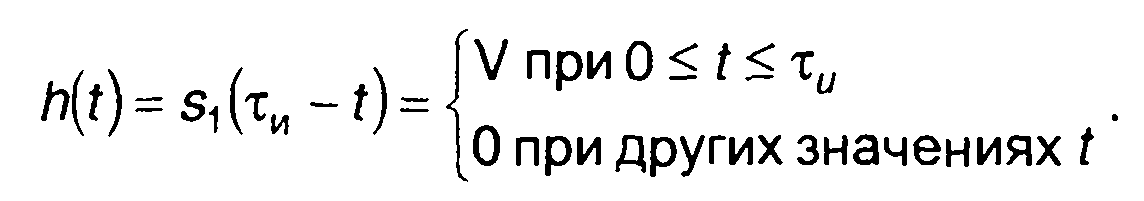
Такую импульсную характеристику имеет интегрирующая цепь с постоянной времени х_и.

Другой пример согласованного фильтра приведен в разд. 11 - рассматривается фильтр, согласованный с ЛЧМ сигналом.

Максимальное отношение сигнал/шум на выходе согласованно­го фильтра определяется с учетом следующего:

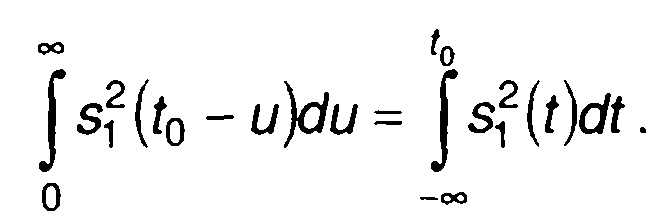(21.51)

Выражение (21.51) определяет энергию сигнала за интервал времени до момента t₀. Таким образом, максимальное отношение

сигнал/шум на выходе согласованного фильтра равно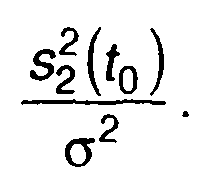

Рассмотрение проводилось для случая воздействия на цепь бе­лого шума. Однако тот же подход может быть использован и в об­щем случае - при воздействии на цепь шума, имеющего произ­вольную спектральную плотность мощности.

В ряде случаев целесообразно несколько изменить постановку за­дачи оптимизации: задана структура линейной цепи, необходимо вы­брать параметры цепи таким образом, чтобы обеспечивалось макси­

максимальное отношение сигнал/шум на выходе. В качестве примера тако­го подхода рассмотрим RС-цепь с импульсной характеристикой

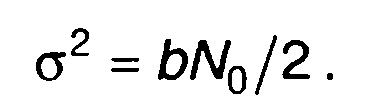
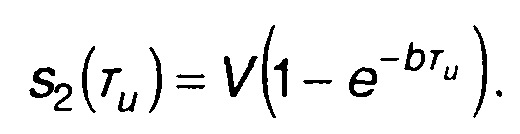
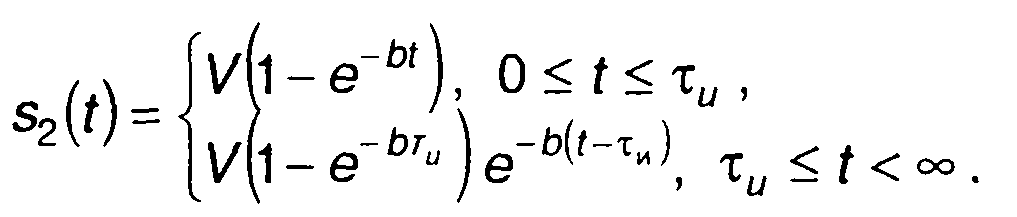
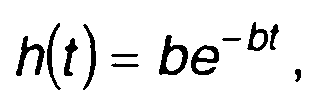
где 1/b = RC- постоянная времени цепи.

При воздействии на цепь сигнала в виде прямоугольного им­пульса сигнал на выходе цепи описывается выражением (рис. 21.5)

Сигнал на выходе цепи достигает максимального значения в момент времени t = τ_и . Таким образом, имеем

Дисперсия шума на выходе цепи равна

Следовательно, отношение сигнал/шум определяется выраже­нием

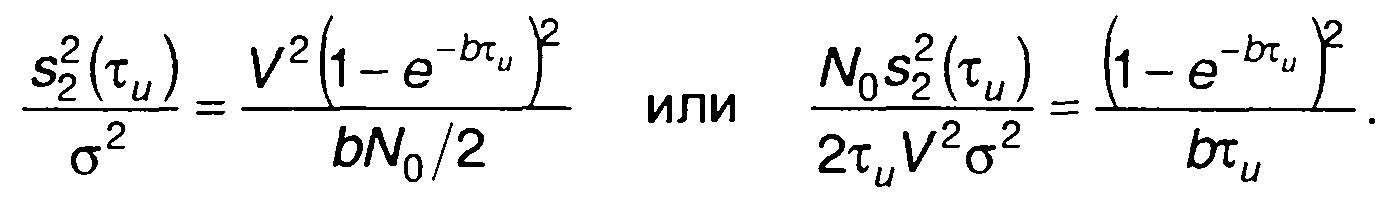
Это отношение зависит от выбора постоянной времени цепи 1/b (рис. 21.6). Значение b, при котором отношение сигнал/шум достигает максимального значения, определяется из условия

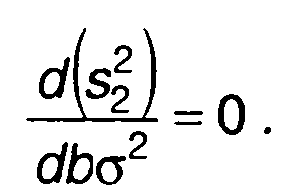
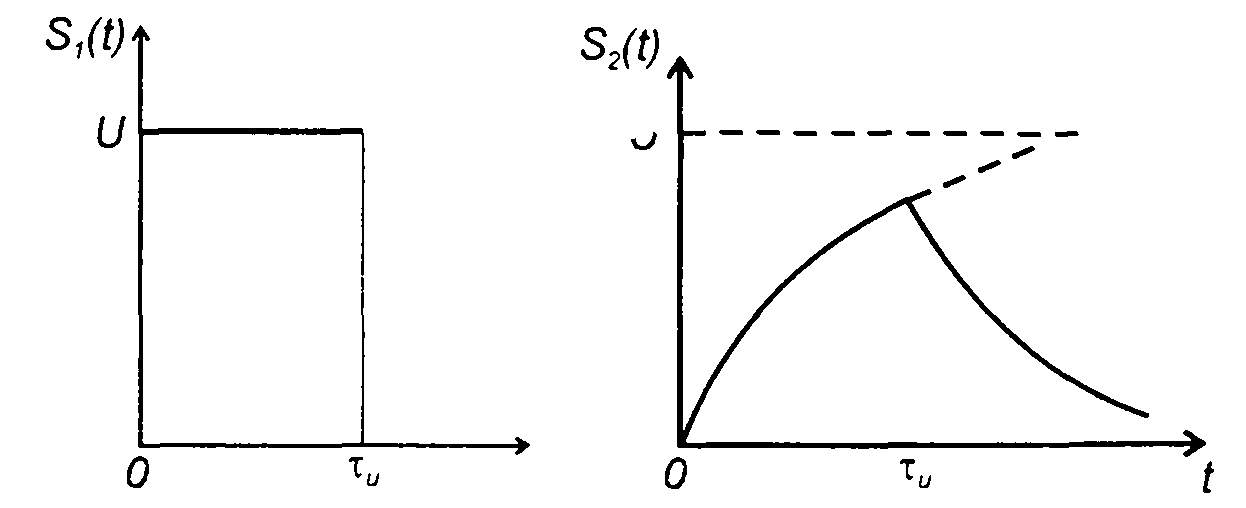
Рис. 21.5

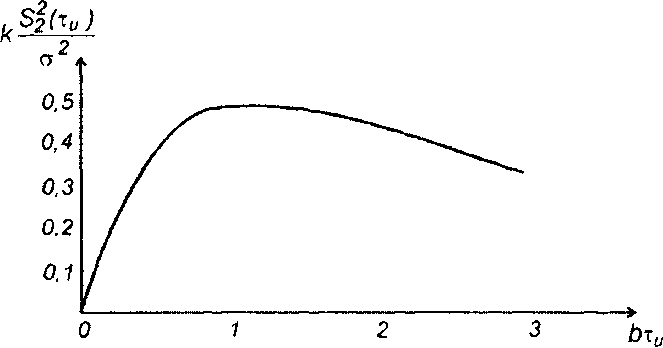
Рис. 21.6

С учетом выражения для отношения сигнал/шум условие, по­зволяющее находить значение b, соответствующее максимуму, запишется в виде

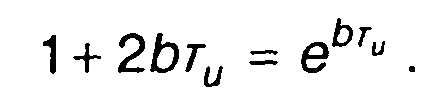
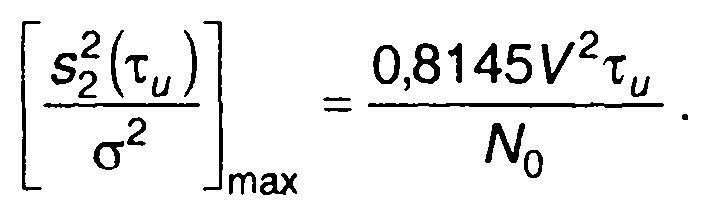
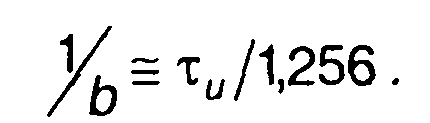
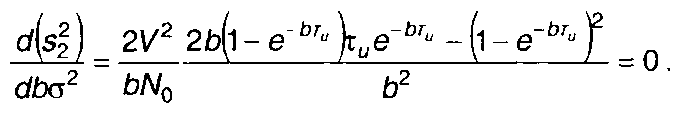
От записанного выражения можно перейти к следующему

Решение последнего уравнения дает следующее значение по­стоянной времени цепи

Приведенное значение постоянной цепи соответствует макси­мальному отношению сигнал/шум в момент времени τ_u. Макси­мальное отношение получим при подстановке bτ_u = 1,256 в выра­жение для отношения сигнал/шум

Раздел 22.

НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

В разделе описываются основные методы анализа случайных процессов на выходе нелинейных устройств. Рассмотрение про­водится для безынерционных преобразователей, отклик которых в выбранный момент времени является функцией воздействия в тот же момент времени. Описание методов иллюстрировано при­мерами, полезными для практики исследования случайных про­цессов.

В разд. 15 и 17 приведены выражения для ПРФ или ФРВ слу­чайного процесса после его преобразования. Однако анализ на их основе часто сопряжен с трудностями, не всегда преодолимыми на практике. По этой причине при рассмотрении нелинейных преобра­зований часто ограничиваются менее полными характеристиками случайного процесса, в первую очередь, корреляционной функцией и спектром. Описания случайного процесса на выходе преобразо­вателя с использованием только указанных характеристик расши­ряет число возможных подходов к анализу, которые требуют от­дельного рассмотрения.

22.1. Прямой метод определения характеристик случайного процесса на выходе нелинейного устройства

Прямой метод анализа основан на использовании соотношений, связывающих характеристики распределения случайного процесса на входе ξ(t) и выходе устройства ξ(t). Если на вход нелинейного устройства, имеющего характеристику

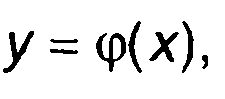(22.1)

которая задает взаимно однозначное соответствие х и у, воздейст­вует случайный процесс ξ(t). имеющий ПРВ f_ξ1(x), то ПРВ случай­ного процесса на выходе η(t) определяется соотношениями, при­веденными в разд. 15.

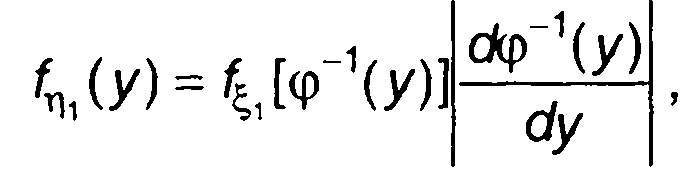(22.2)

где φ^-1 (у)-функция, обратная φ(х).

Математическое ожидание случайного процесса на выходе не­линейного устройства может быть найдено как

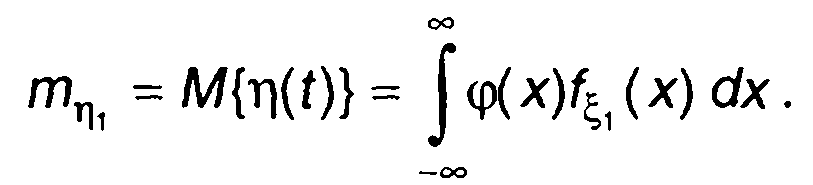(22.3)

Момент п-го порядка:

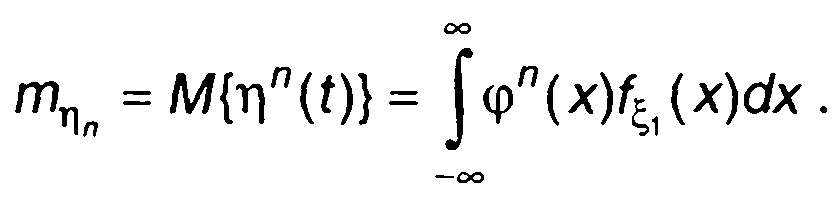(22.4)

Второй начальный момент (ковариационная функция) случайно­го процесса на выходе определяется с использованием двумерной ПРВ случайного процесса на входе f_ξ2{х₁,х₂) выражением

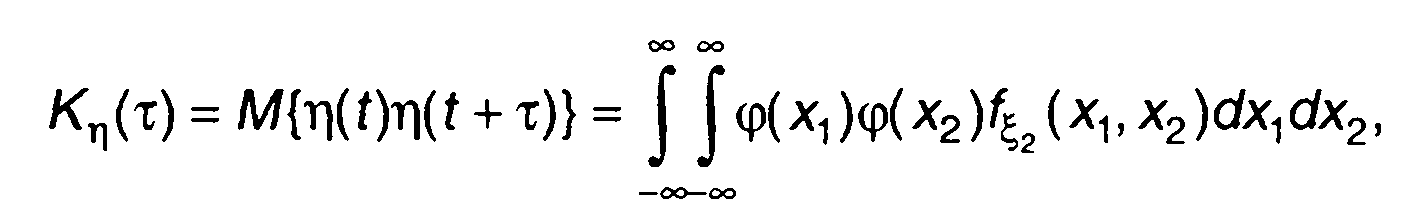(22.5)

где X₁, х₂ - значения случайного процесса ξ(t) в моменты времени t и t + τ.

Корреляционная функция случайного процесса на выходе нели­нейного преобразователя равна

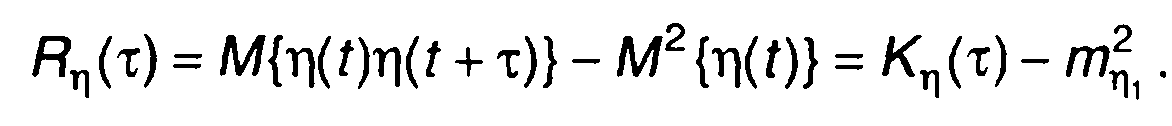(22.6)

При определении корреляционной функции может оказаться полезным разложение двумерной ПРВ случайного процесса ξ(t) в ряд по ортонормированной системе многочленов (разд. 16)

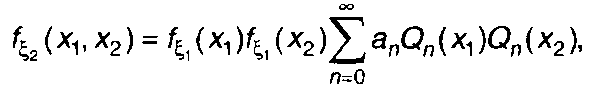(22.7)

где {Q_n(x)} - ортогональная система функций;

Нелинейные преобразования случайных процессов

Подставив (22.7) в (22.5), получим

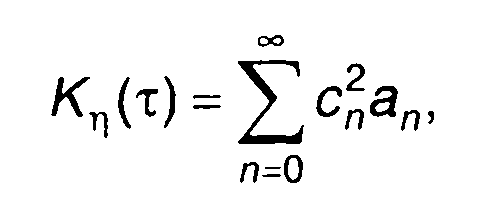(22.8)

где

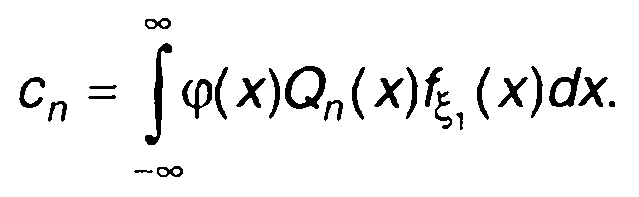(22.9)

Конкретизируем полученное выражение для случая стационар­ного гауссовского процесса на входе

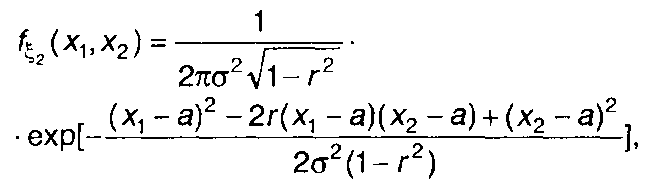(22.10)

где а, σ², r — математическое ожидание, дисперсия и нормирован­ная корреляционная функция случайного процесса ξ(t).

Ковариационная функция случайного процесса на выходе нелиней­ного устройства η(t) определяется (22.5) с подстановкой в него (22.10)

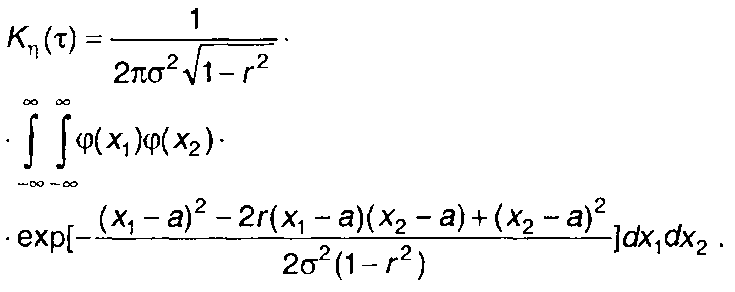(22.11)

Переходя к нормированным величинам и обозначая a/σ=q, выражение (22.11) запишем в виде

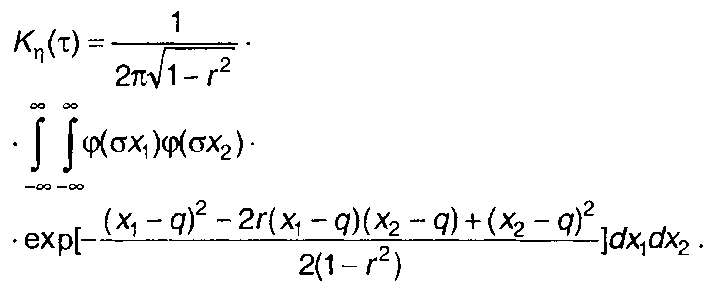(22.12)

Используя разложение двумерной ПРВ гауссовского процесса ξ(t) в ряд по многочленам Эрмита (разд. 6)

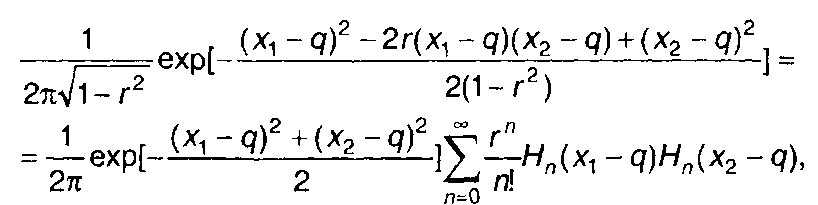(22.13)

где Н_п(х) - многочлен Эрмита, выражение для К_η(т) получим в виде

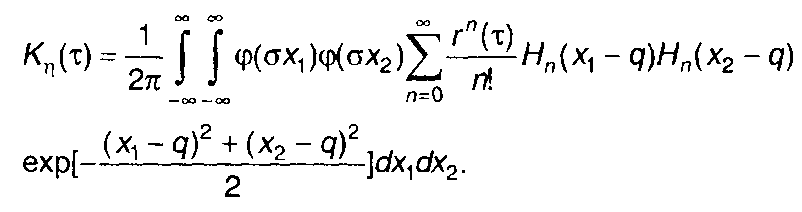(22.14)

Разделив переменные интегрирования в (22.14), запишем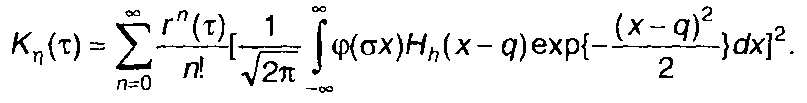

Обозначим

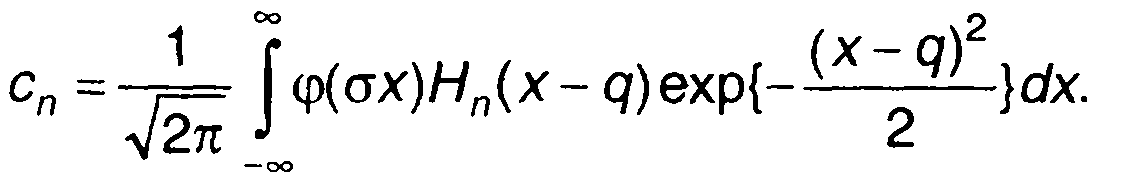(22.15)

Выражение для Кη(τ) примет вид

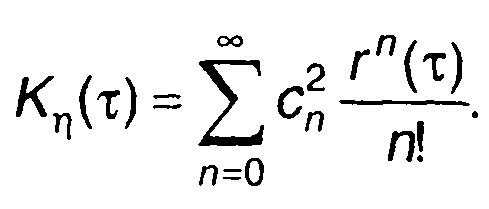(22.16)

Таким образом, записано выражение для ковариационной функции на выходе нелинейного устройства в виде ряда, члены которого содержат степени r(т) и коэффициенты сn, определяе­мые характеристикой нелинейного устройства.

Спектральную плотность мощности случайного процесса на вы­ходе нелинейного устройства N_η(ω) определим исходя из (22.16)

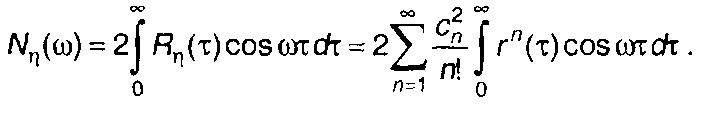(22.17)

При расчёте (22.17) можно воспользоваться следующим при­ближенным решением [16]

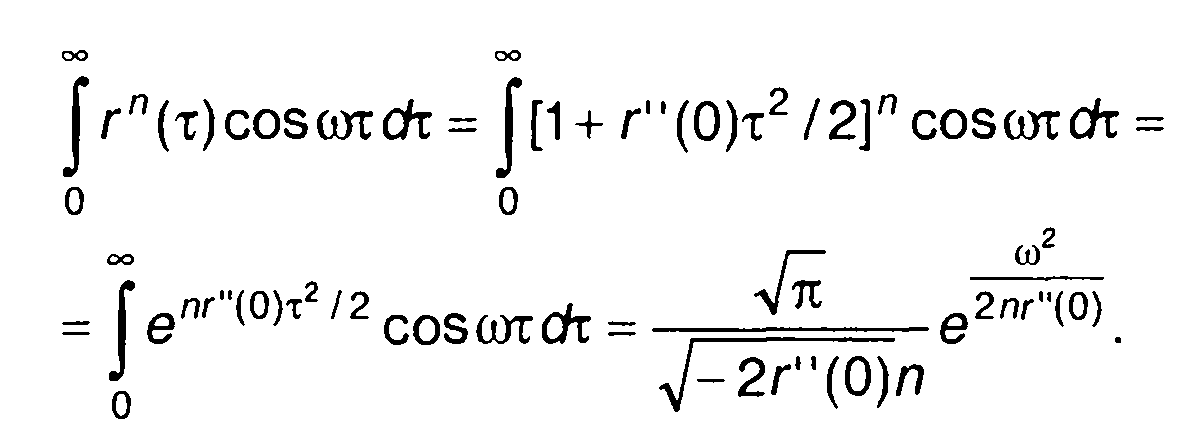(22.18)

С учетом приведенного приближенного решения выражение для спектра на выходе нелинейного устройства запишется в виде

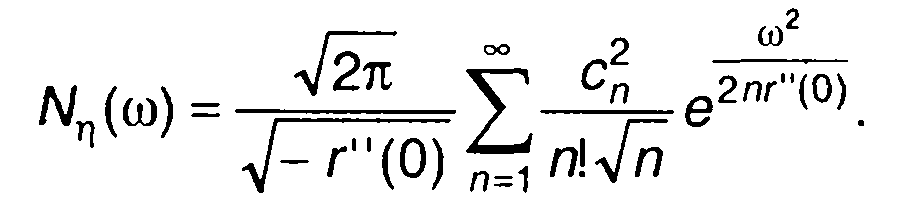(22.19)

Как следует из (22.19), спектральная плотность мощности слу­чайного процесса на выходе нелинейного устройства описывается выражением в виде ряда, члены которого определяются корреля­ционной функцией случайного процесса на входе (ее второй про­изводной при т = 0) и характеристикой нелинейного устройства.

В качестве примеров рассмотрим характеристики случайных процессов на выходе некоторых видов нелинейных устройств, на­ходящих достаточно широкое применение в радиотехнике. Помимо иллюстрации возможностей изложенного подхода, рассматривае­мые примеры представляют и самостоятельный интерес.

22.2. Случайный процесс на выходе нелинейного устройства со степенной характеристикой

Одним из узлов радиотехнических систем различного назначе­ния является детектор. Он представляет последовательно вклю­ченные нелинейный элемент и фильтр. Нелинейный элемент обычно имеет степенную характеристику, одностороннюю или дву­стороннюю. Ниже рассматриваются нелинейные элементы с ли­нейной и квадратичной характеристиками.

22.2.1. Односторонняя линейная характеристика

Характеристика нелинейного устройства имеет вид (рис. 22.1)

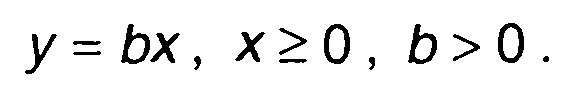(22.20)

Функция распределения вероятностей случайного процесса на выходе такого устройства η(t) определяется как

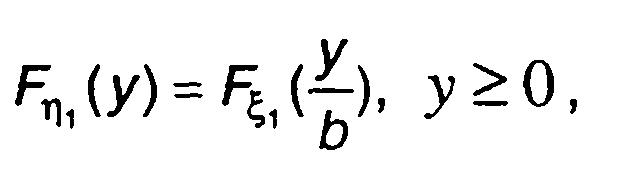(22.21)

где F_ξ1(x) - ФРВ случайного процесса на входе.

Переходя к ПРВ случайного процесса η(t), получим

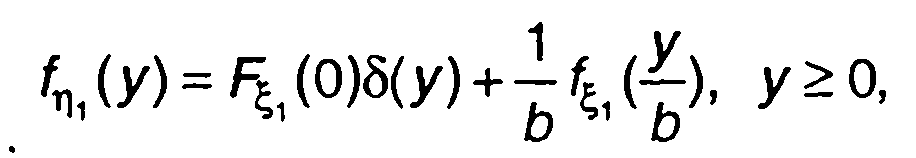(22.22)

где f_ξ1(x) - ПРВ случайного процесса на входе ξ(t); δ(t) - им­пульсная функция.

Моменты распределения вероятностей n-го порядка случайного процесса на выходе устройства определяются выражением

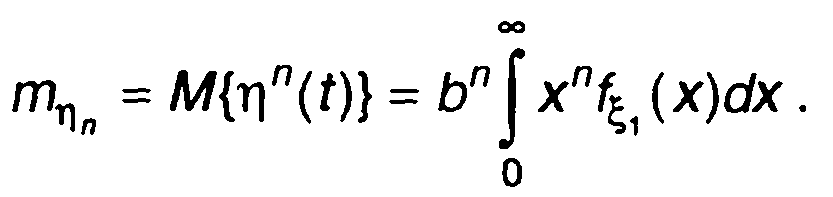(22.23)

Если f_ξ1(x) является четной функцией, то моменты распреде­ления четных порядков случайного процесса на выходе устройства (22.23) можем получить в виде

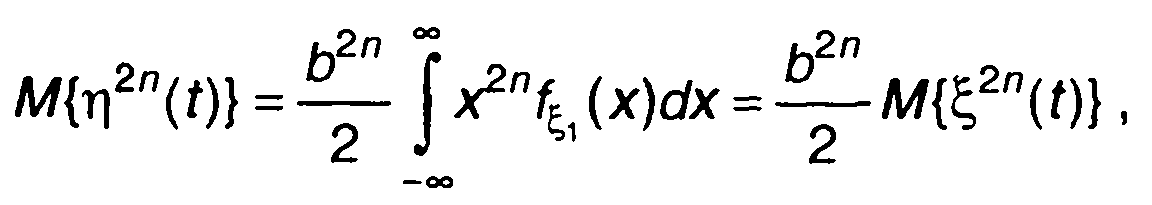(22.24)

т. е. выразить через моменты распределения четных порядков случайного процесса на входе.

Рис. 22.1

Ковариационная функция случайного процесса на выходе уст­ройства определяется как

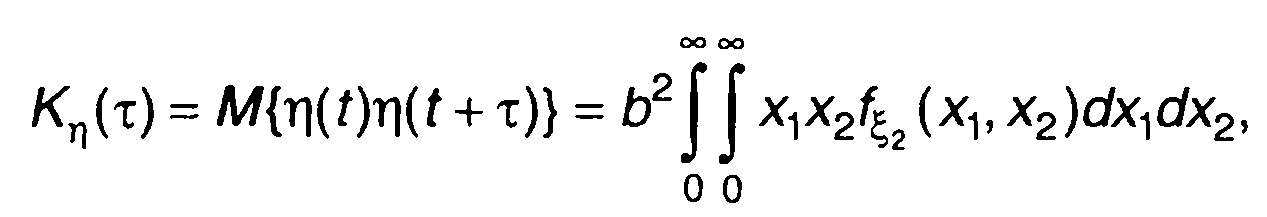(22.25)

где f_ξ1(x₁,x₂) - двумерная ПРВ случайного процесса на входе ξ(t);

x₁,x₂ - значения ξ(t) в моменты времени t и t + т.

Конкретизируем полученные результаты применительно к нор­мальному и релеевскому распределению случайного процесса на входе нелинейного устройства.

Нормальное распределение. Для центрированного гауссов­ского процесса на входе, имеющего ПРВ

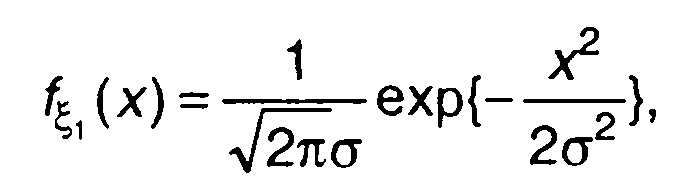
из (22.22) получим

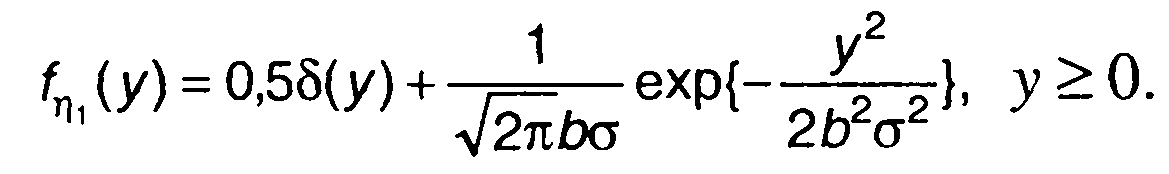(22.26)

График f_η1(х) изображен на рис. 22.2.

Учитывая четность функции ПРВ гауссовского процесса, момен­ты распределения вероятностей η(t) четных порядков найдем из (22.24)

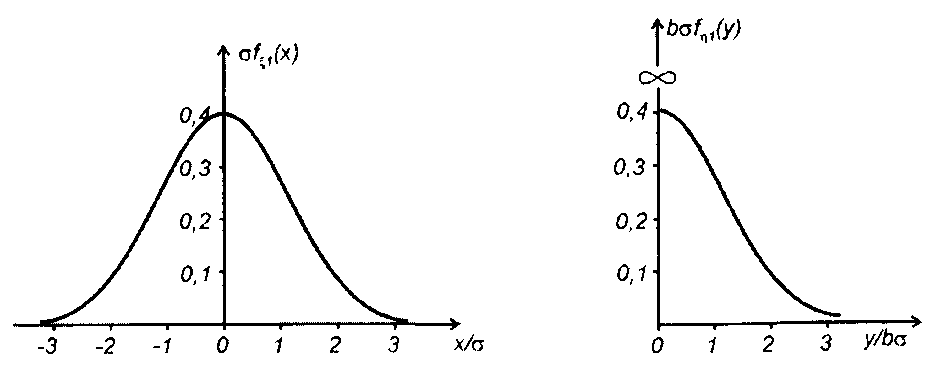
Рис. 22.2

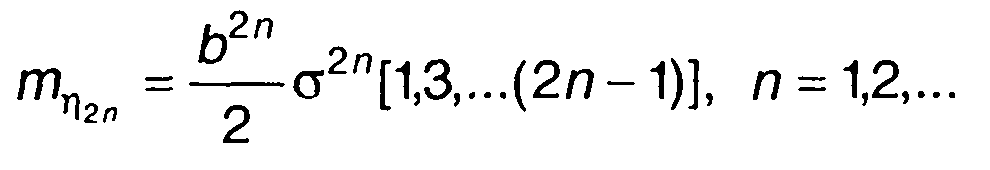(22.27)

Моменты нечетных порядков находятся непосредственно из (22.23)

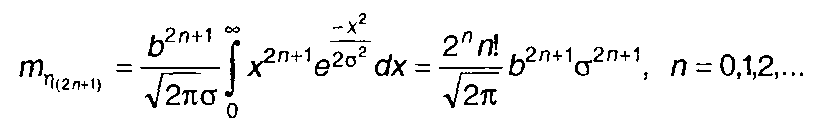(22.28)

В частности, математическое ожидание η(t) равно

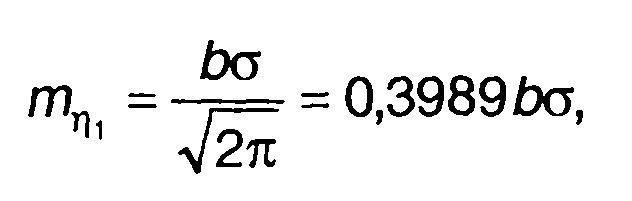
дисперсия

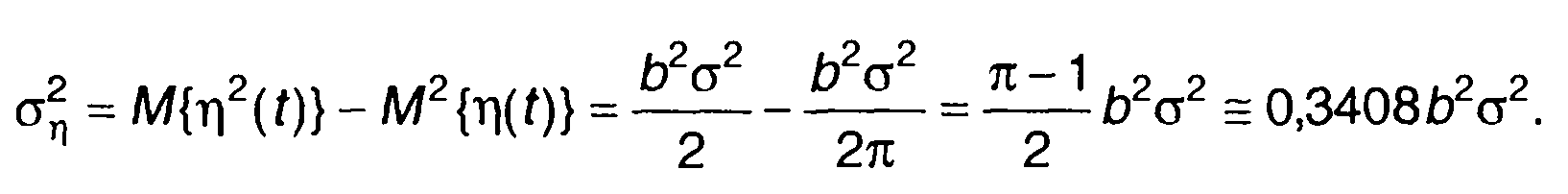
Ковариационная функция случайного процесса на выходе нели­нейного устройства определяется из (22.11) с учетом выражения для двумерной ПРВ гауссовского процесса (а = 0)

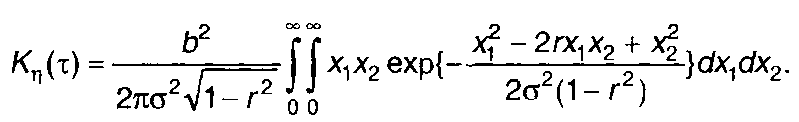(22.29)

Решение двойного интеграла в (22.29) дает

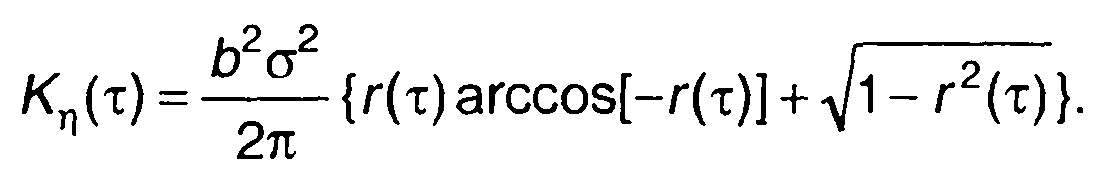(22.30)

Аналогичный результат получается при использовании разло­женияK_η(τ) в ряд (22.16). Коэффициенты ряда описываются

(22.15)

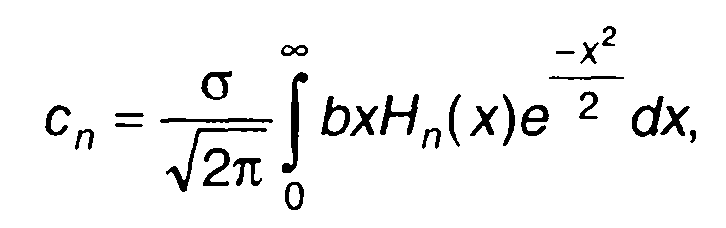(22.31)

где Н_п(х) - многочлен Эрмита.

Из (22.31) находятся следующие выражения для с_n

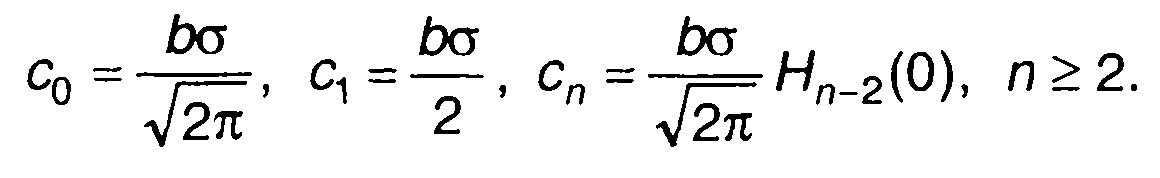(22.32)

Подставляя (22.31) в (22.16), выражение для К_η(т) запишем в виде

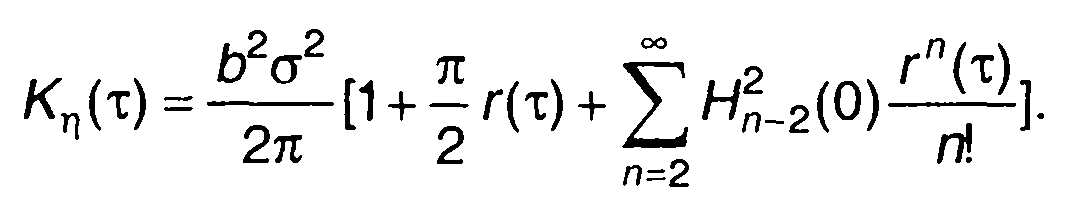(22.33)

С учетом следующих равенств для многочленов Эрмита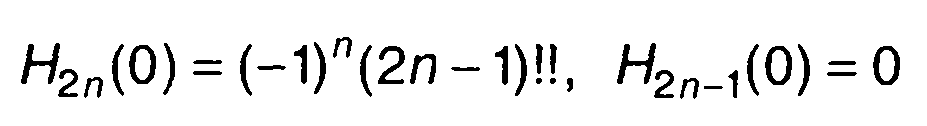

выражение для К_η(т) получается из (22.33) в виде

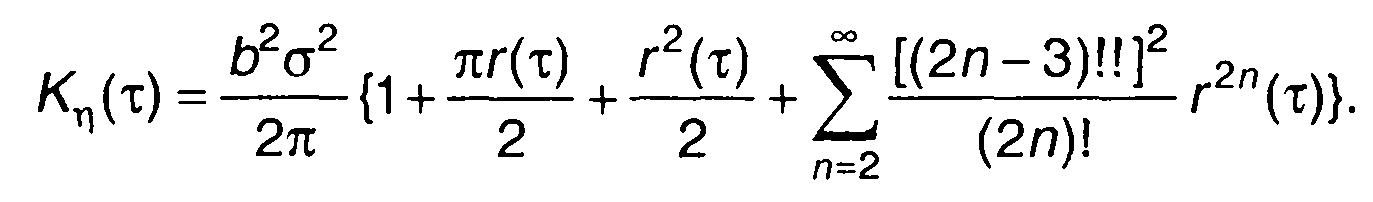
От него перейдем к следующему

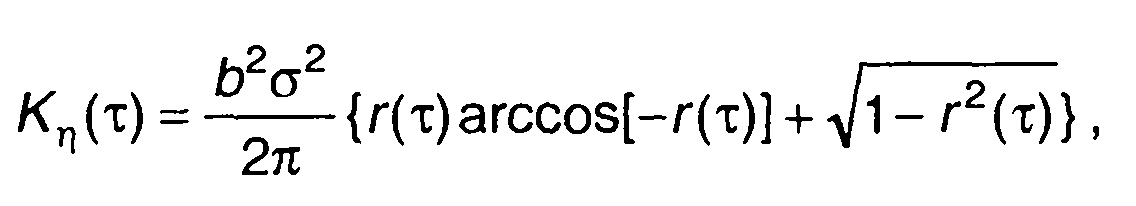
что совпадает с (22.30).

С учетом полученного результата запишем выражения для кор­реляционной функция и дисперсии случайного процесса на выходе

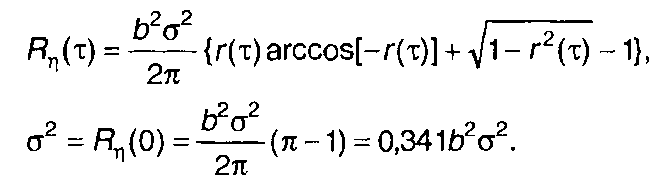(22.34)

Спектральная плотность мощности случайного процесса на вы­ходе нелинейного устройства определяется преобразованием Фу­рье (22.34)

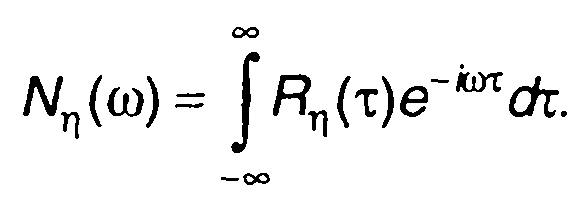(22.35)

Для удобства вычисления (22.35) целесообразно R_η(т) пред­ставить в виде ряда. С этой целью используем разложения

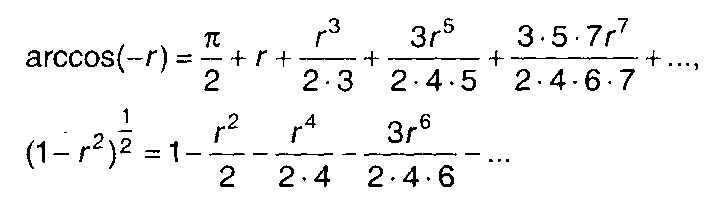
Ограничиваясь членами, содержащими r в степени не выше второй, выражение для R_η(т) получим в виде

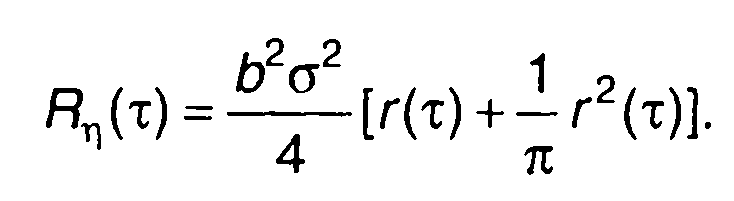(22.36)

Подставляя (22.36) в (22.35), находим

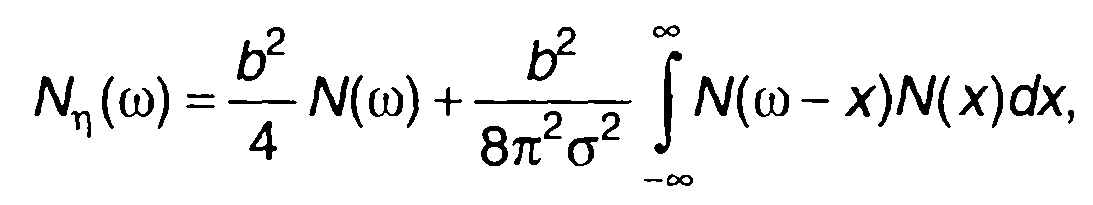(22.37)

где N(ω) - спектральная плотность мощности случайного процесса на входе.

В качестве примера рассмотрим случайный процесс, имеющий спектральную плотность мощности

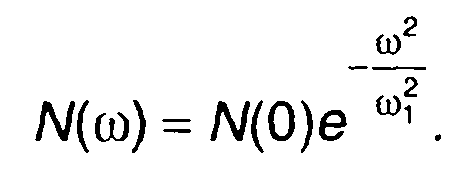
Ей соответствует корреляционная функция

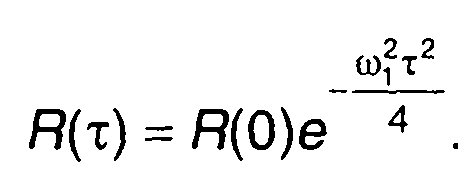
Спектральная плотность мощности случайного процесса на вы­ходе нелинейного устройства описывается выражением

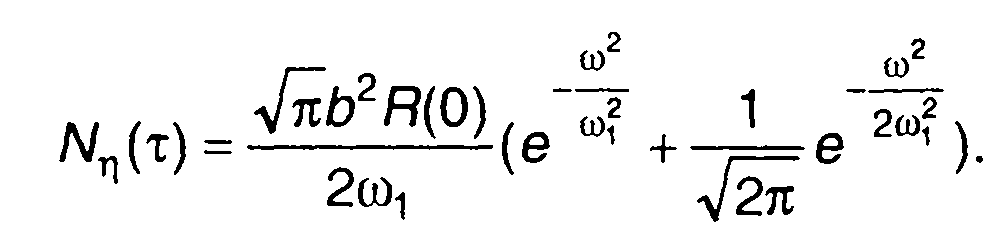
Релеевское распределение. Практический интерес представ­ляет нелинейное преобразование (22.20) случайного процесса ξ(t), имеющего релеевское распределение. Такое распределение имеет огибающая узкополосного гауссовского процесса (разд. 20). Одномерная и двумерная ПРВ ξ(t) описываются выражениями

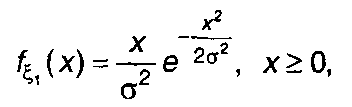(22.38)

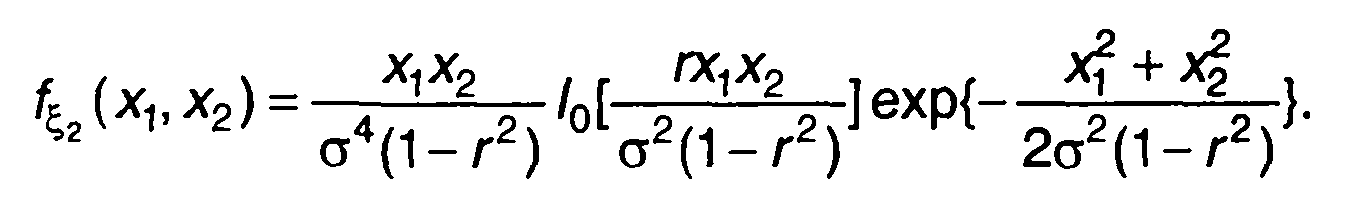(22.39)

Плотность распределения вероятностей случайного процесса на выходе устройства находится из (22.22) с учетом (22.38)

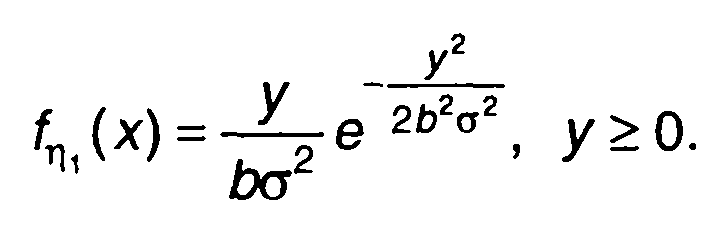(22.40)

Моменты распределения вероятностей η(t) определяются как

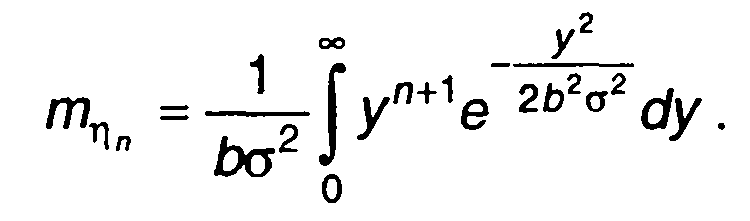(22.41)

Моменты распределения нечетных порядков: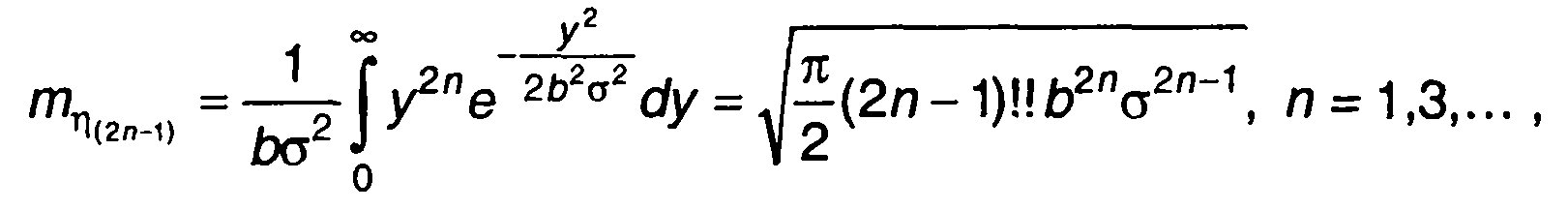

четных порядков:

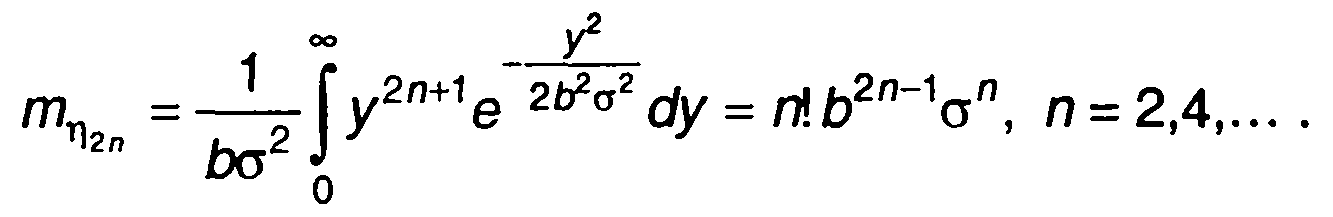
Математическое ожидание и дисперсия равны

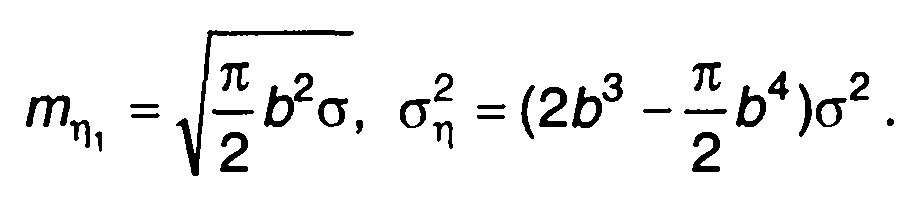(22.42)

Выражение для ковариационной функции η(t) запишем, под­ставляя (22.39) в (22.25)

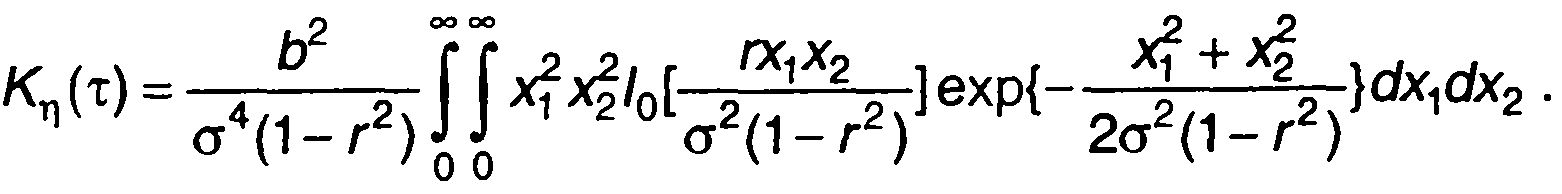(22.43)

Решение (22.43) с использованием соотношения

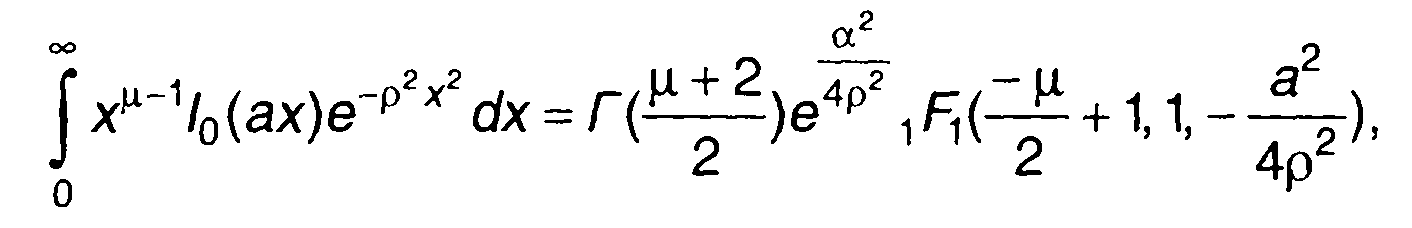(22.44)

где Г(х) - гамма-функция; ₁ F ₁(х₁, х₁, х₁) - гипергеометрическая функция, в виде

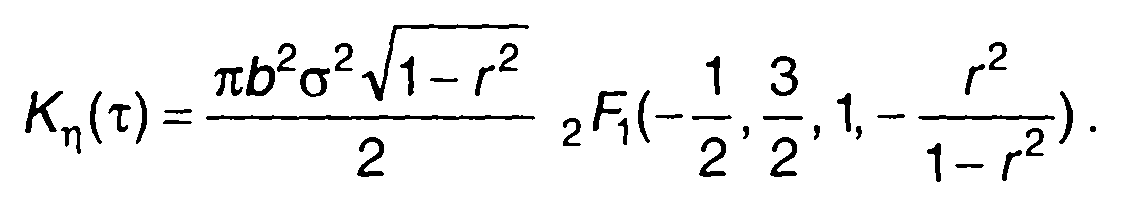(22.45)

Преобразование гипергеометрической функции приводит (22.45) к следующему виду

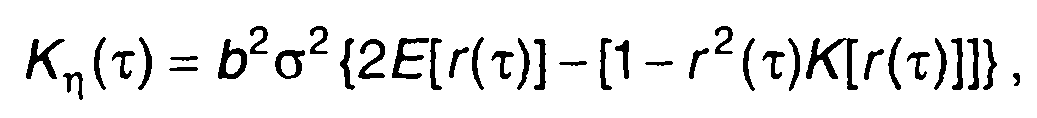(22.46)

где К{х} - полный эллиптический интеграл первого рода; Е (х) - полный эллиптический интеграл второго рода.

22.2.2. Односторонняя квадратичная характеристика

Характеристика нелинейного устройства имеет вид (рис. 22.3)

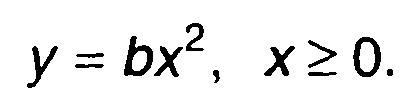(22.47)

Функция распределения вероятности случайного процесса на выходе определяется выражением

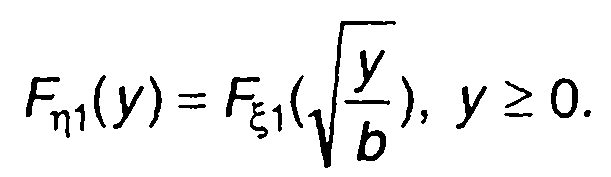(22.48)

Плотность распределения вероятности случайного процесса на выходе равна

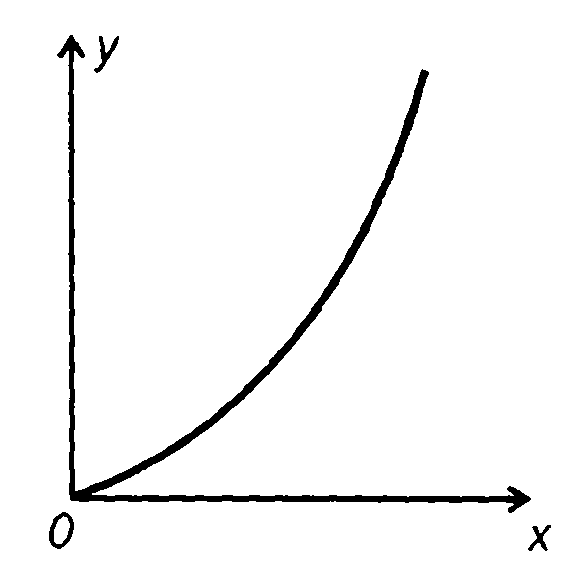
Рис. 22.3

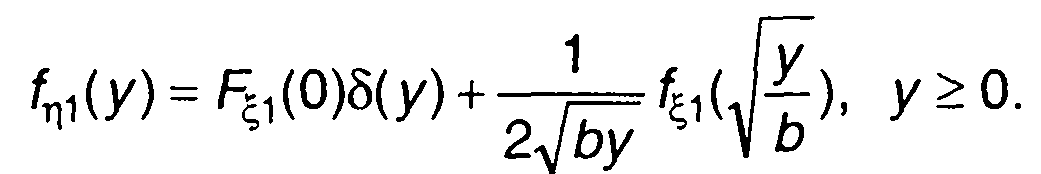(22.49)

Начальные моменты η(t) определяются выражением

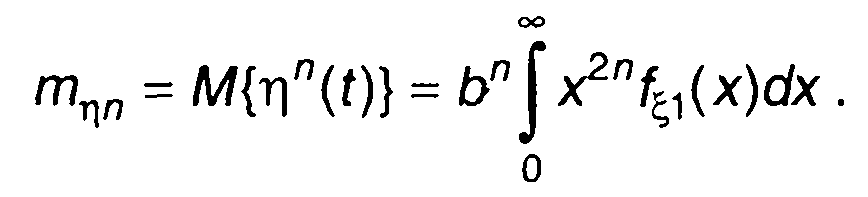(22.50)

Ковариационная функция случайного процесса на выходе уст­ройства

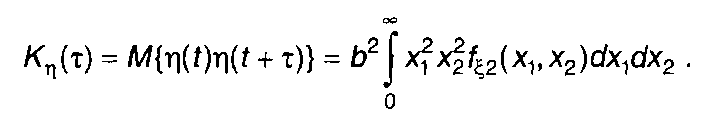(22.51)

Конкретизируем полученные выражения для нормального и релеевского распределения случайного процесса на входе ξ(t)

1. Нормальное распределение.

Для гауссовского процесса на входе

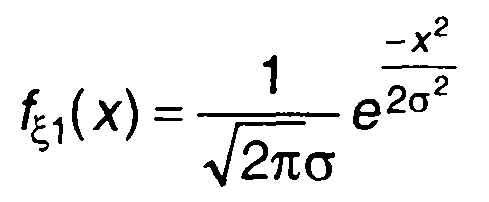
из (22.49) получим (рис. 22.4)

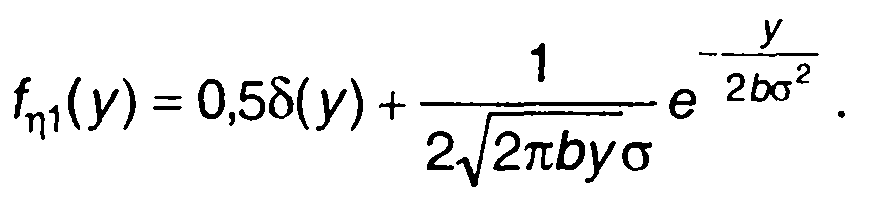(22.52)

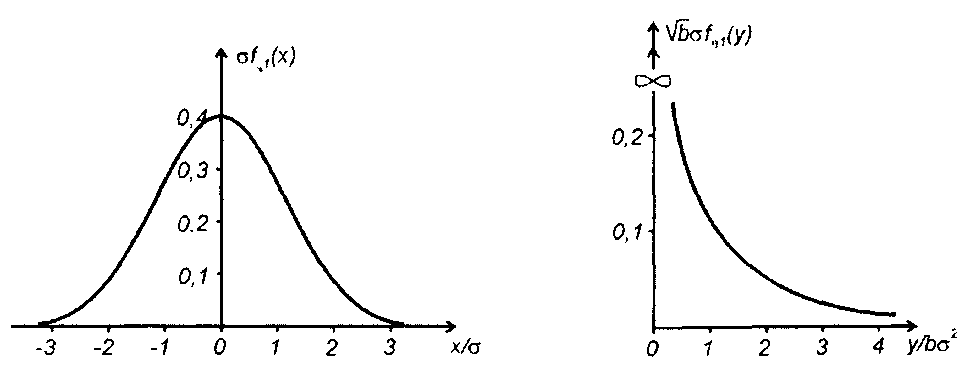
Рис. 22.4

Начальные моменты n-го порядка определяются выражением

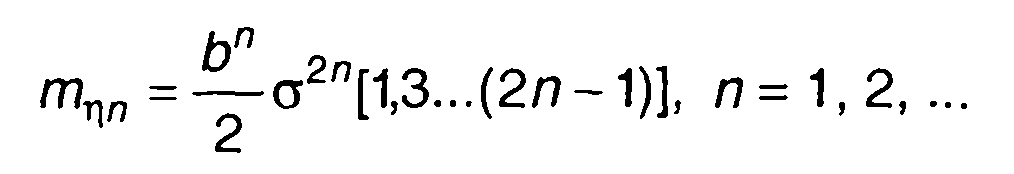(22.53)

2. Релеевское распределение.

Плотность распределения вероятности случайного процесса на входе определяется (22.38). Из (22.49) получим

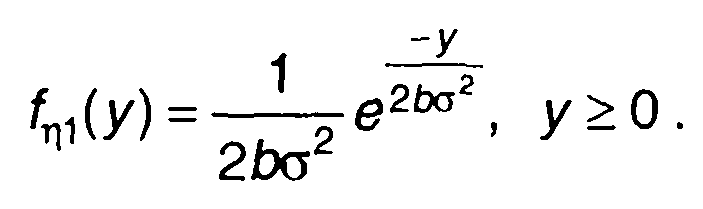(22.54)

Момент n-го порядка:

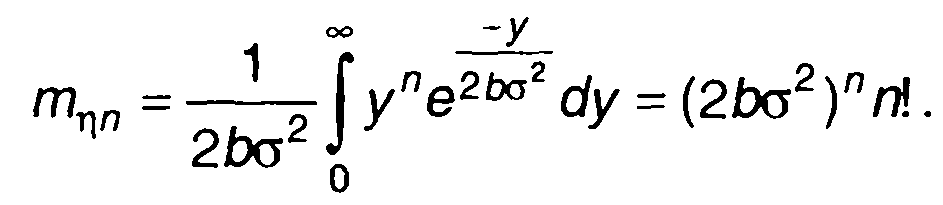(22.55)

Ковариационная функция η(t) определяется (22.5). С учетом (22.39) и (22.47) запишем

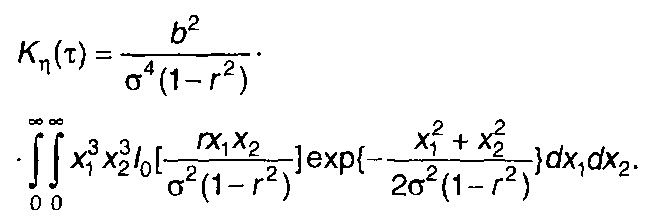(22.56)

Произведя замену переменных z₁ = x₁², z₂ = x₂², (22.56) перепи­шем в виде

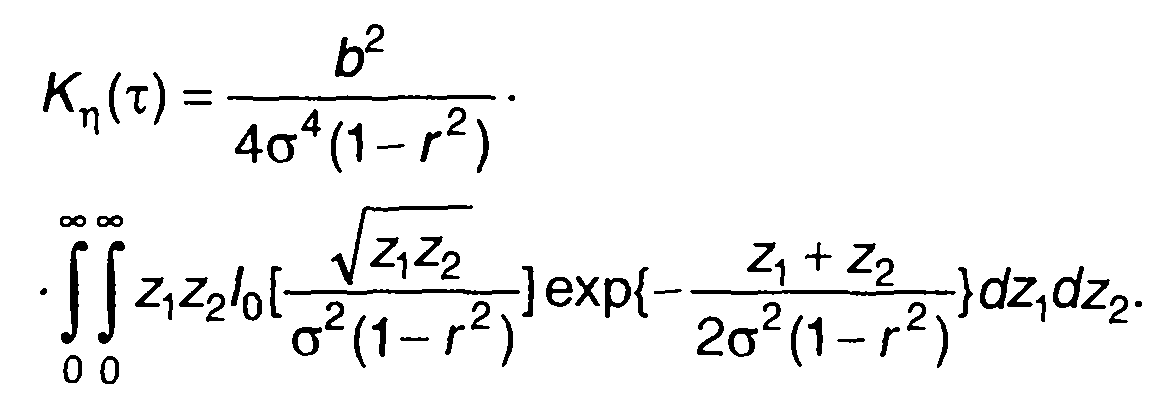(22.57)

Разложение функции Бесселя в ряд

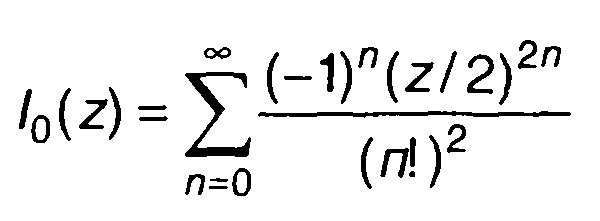
и почленное интегрирование в (22.57) дает

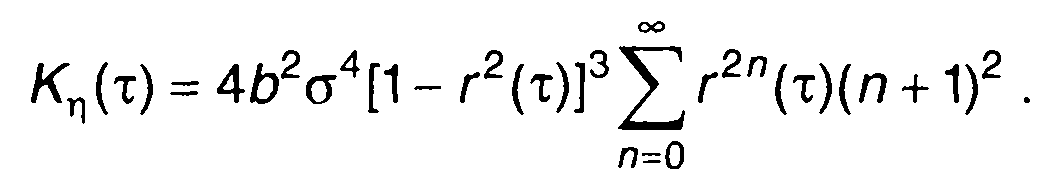(22.58)

С учетом равенства

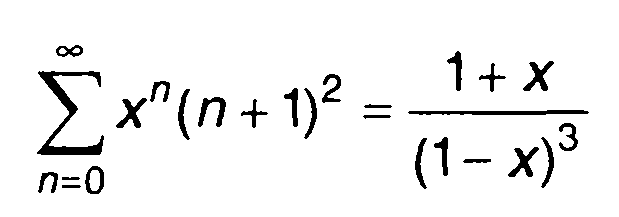
из (22.57) получим

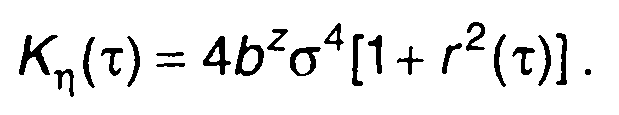(22.59)

Корреляционная функция η(t)

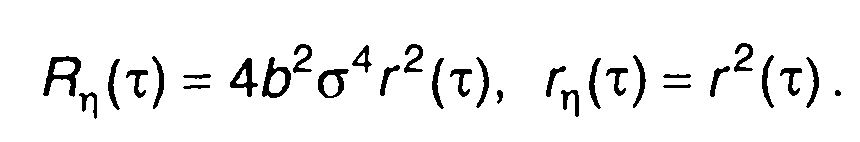(22.60)

Ковариационную функцию случайного процесса на выходе рас­сматриваемого нелинейного устройства можно также определить, используя разложение двумерной ПРВ по ортогональным много­членам. В качестве ортогональной системы многочленов для ПРВ целесообразно выбрать систему многочленов Лагерра, а в качест­ве весовой функции - одномерную ПРВ.

Двумерную ПРВ случайного процесса на выходе устройства найдем, используя подход, изложенный в разд. 17. Двумерная ПРВ случайного процесса на входе описывается (22.39). Переходя от переменных х₁, и х₂ к переменным

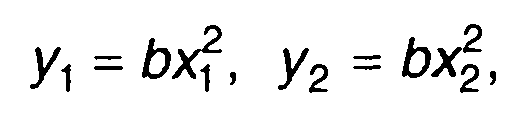(22.61)

получим якобиан преобразования

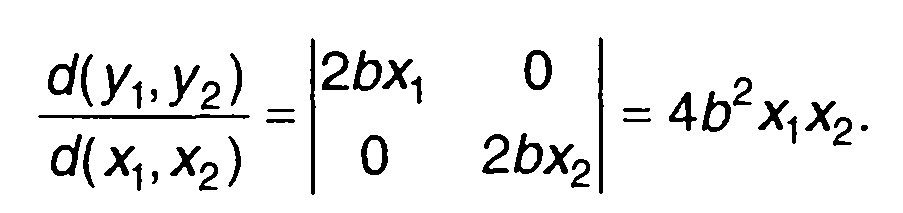(22.62)

Двумерная ПРВ η(t) будет иметь вид

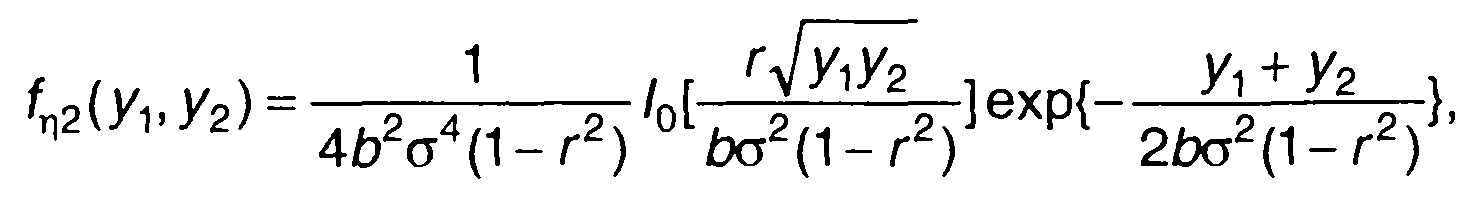(22.63)

где I₀ (х) - модифицированная функция Бесселя первого рода.

При r=0(τ→∞) имеем

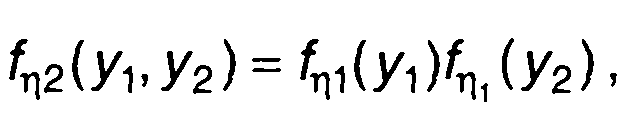
где одномерные ПРВ f_η1(y) описываются (22.38).

Разложение двумерной ПРВ (22.63) в ряд по многочленам Ла­герра имеет вид

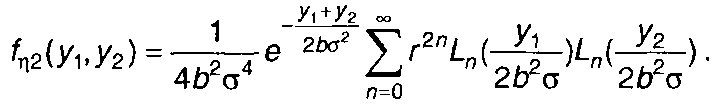(22.64)

Используя разложение (22.64), выражение для ковариационной функции случайного процесса на выходе устройства η(t) запишем в виде

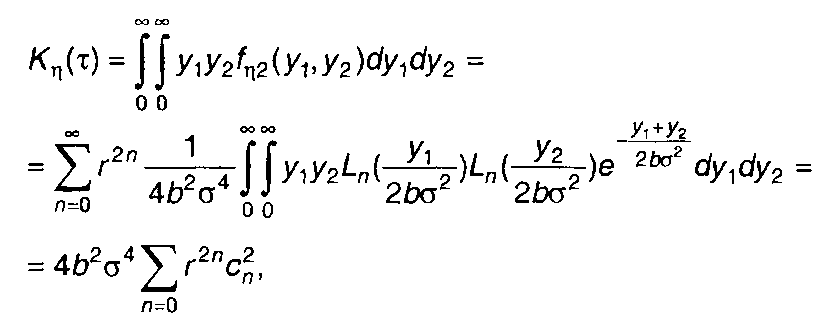(22.65)

где

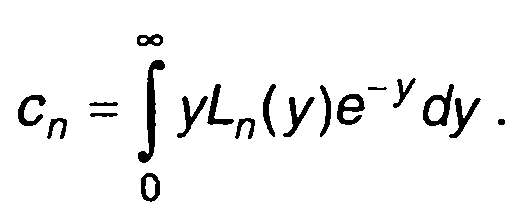
С учетом определения многочленов Лагерра (разд. 15) найдем

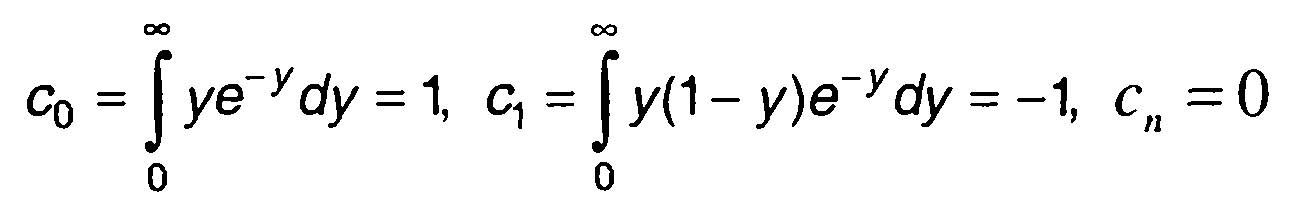
при n≥2. (22.66)

Подставив значения коэффициентов с_nв (22.65), получим

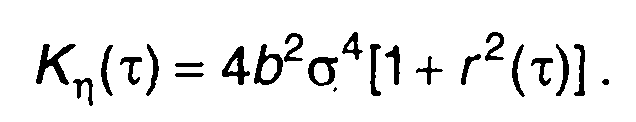(22.67)

Корреляционная функция случайного процесса на выходе

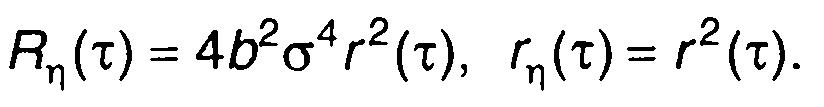(22.68)

22.2.3. Двусторонняя квадратичная характеристика

Характеристика нелинейного устройства имеет вид (рис. 22.5)

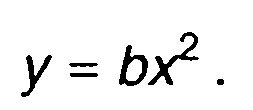(22.69)

Плотность распределения вероятности случайного процесса на выходе устройства описывается выражением (разд. 15)

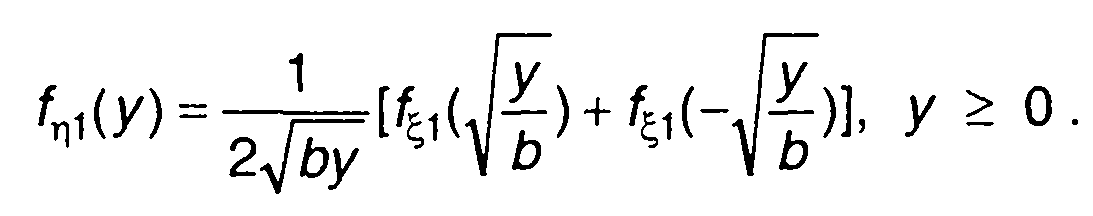(22.70)