ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 26 страница

Момент n-го порядка:

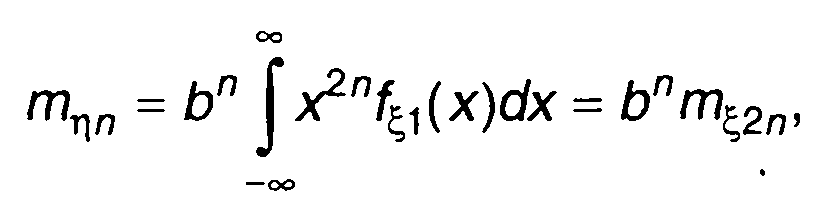(22.71)

где т_ξ2n - момент распределения 2 n-порядка случайного процес­са на входе нелинейного устройства.

Ковариационная функция случайного процесса на выходе уст­ройства определяется выражением

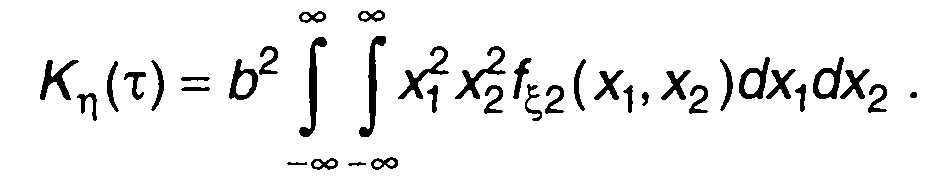(22.72)

1. Нормальное распределение ξ(t).

Для гауссовского процесса на входе из (22.70) получим (рис. 22.6)

Рис. 22.5

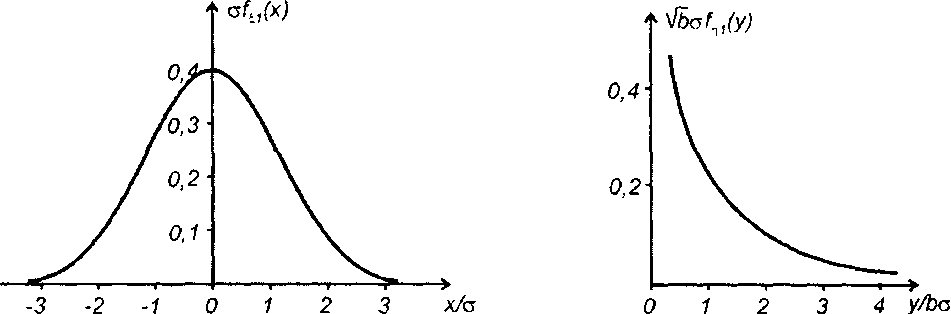
Рис. 22.6

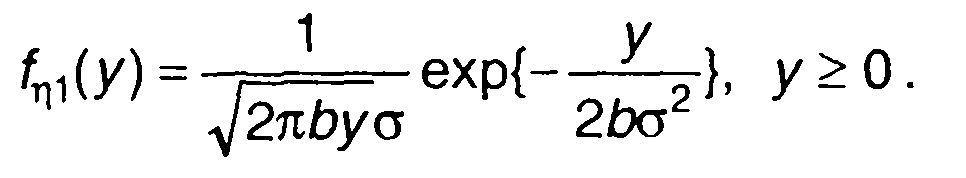(22.73)

Момент n-го порядка равен

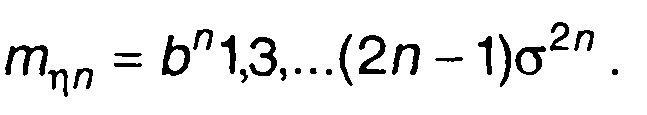(22.74)

В частности, математическое ожидание и дисперсия:

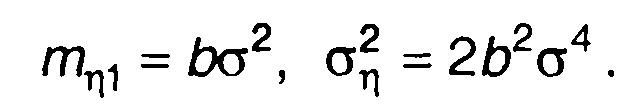(22.75)

Выражение для ковариационной функции случайного процесса на выходе запишем в виде

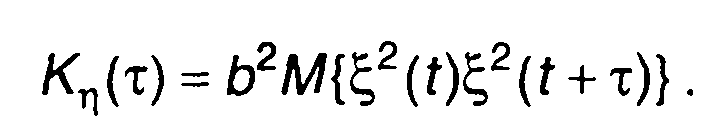(22.76)

Для гауссовского процесса из (22.76) получим

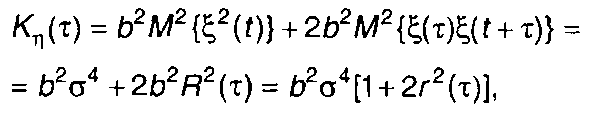(22.77)

где r(т) - нормированная корреляционная функция случайного процесса на входе.

Корреляционная функция η(t)

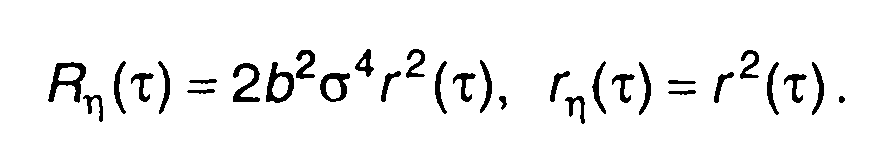(22.78)

Спектральная плотность мощности переменной составляющей случайного процесса на выходе устройства определяется выраже­нием

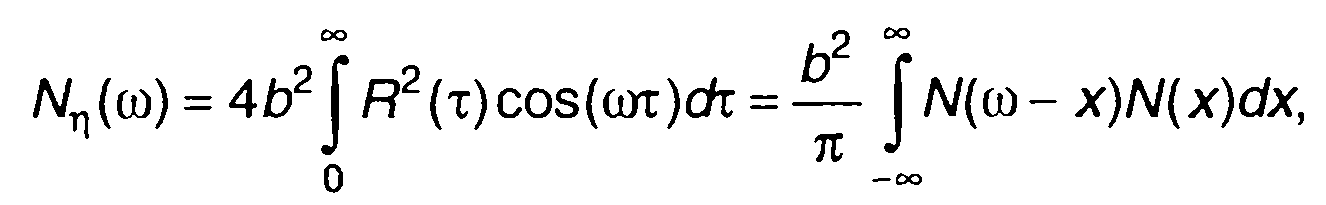(22.79)

где R(т), N(ω) - корреляционная функция и спектральная плотность мощности случайного процесса на входе.

Так для гауссовского процесса на входе, имеющего спектраль­ную плотность и корреляционную функцию

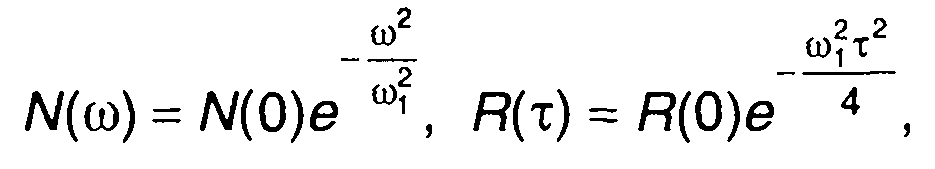
получим

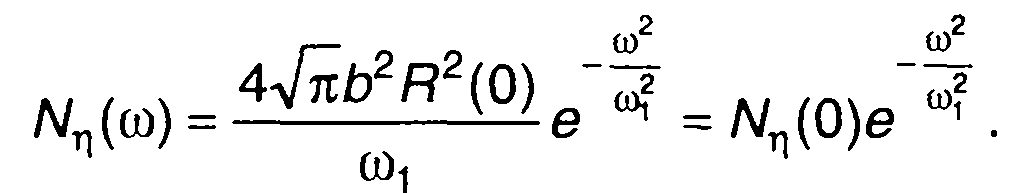
22.3. Метод преобразований

При определении корреляционной функции случайного процес­са на выходе нелинейного устройства может оказаться полезным метод, основанный на использовании преобразования Лапласа характеристики нелинейного устройства. Этот метод анализа не­линейных преобразований гауссовских процессов в некоторых слу­чаях позволяет обойти трудности, с которыми приходится сталки­ваться при применении прямого метода.

22.3.1. Содержание метода

Второй начальный момент случайного процесса на выходе не­линейного устройства η(t) описывается выражением (22.5)

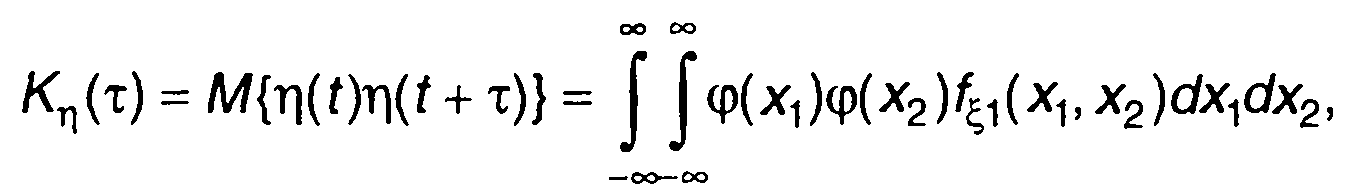(22.80)

где ф(х) - характеристика нелинейного устройства.

Если характеристика нелинейного устройства допускает преоб­разование Лапласа: прямое

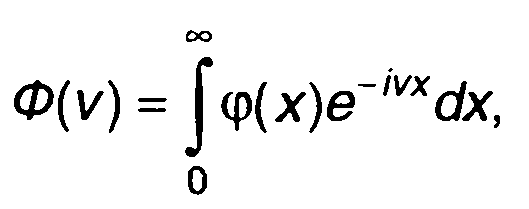
обратное

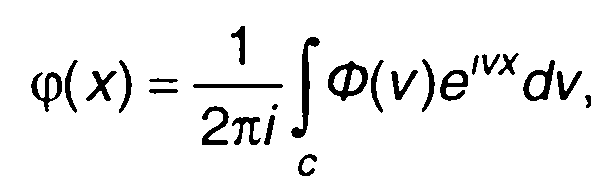(22.81)

где с - контур интегрирования, то, используя преобразование Лап­ласа характеристики нелинейного устройства, (22.80) можем пред­ставить в виде

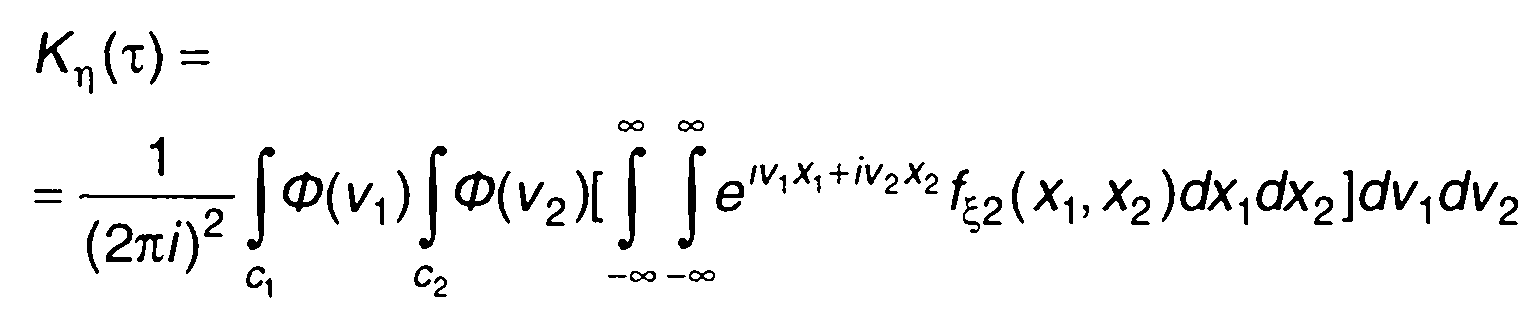(22.82)

Внутренний интеграл в (22.82) представляет двумерную харак­теристическую функцию случайного процесса на входе

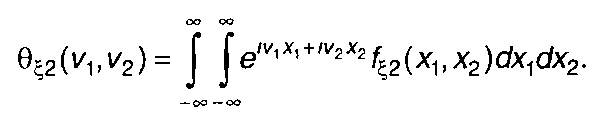(22.83)

Таким образом, выражение для К_η(т) запишется в виде

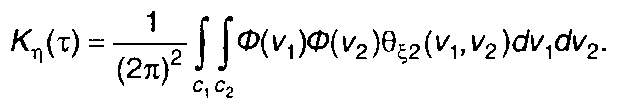(22.84)

Контуры интегрирования для некоторых распространенных ви­дов нелинейных устройств приведены в [20].

Основные трудности при использовании (22.84) связаны с опре­делением двумерной характеристической функции случайного процесса на входе. Для гауссовского процесса характеристическая функция описывается достаточно просто и метод преобразований для ряда характеристик нелинейных устройств оказывается эф­фективным.

Характеристическая функция центрированного гауссовского процесса ξ(t) равна (разд. 16)

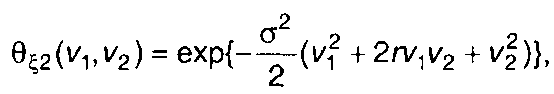(22.85)

где σ², r(т) - дисперсия и нормированная корреляционная функция случайного процесса на входе ξ(t).

Подставив (22.85) в (22.84) и используя разложение экспонен­циального сомножителя в ряд

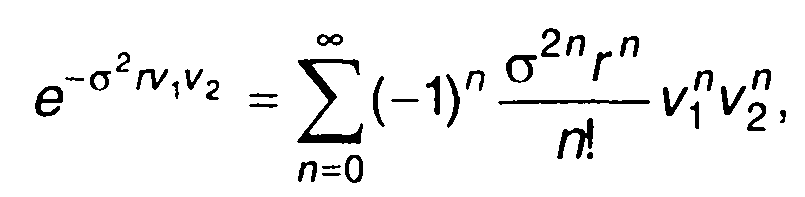(22.86)

получим

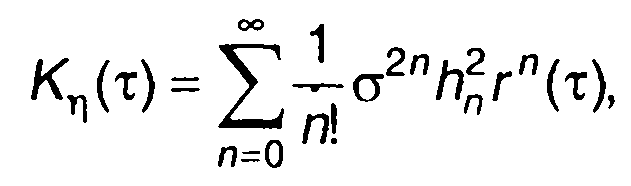(22.87)

где

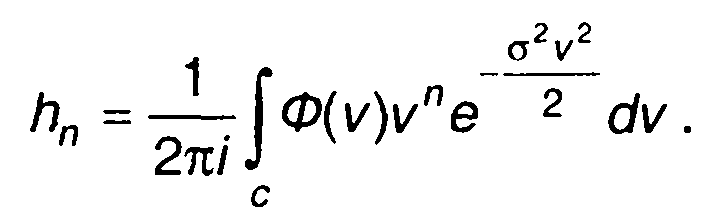(22.88)

Таким образом, записано выражение для ковариационной функции случайного процесса на выходе нелинейного устройства в виде ряда по степеням нормированной корреляционной функции гауссовского процесса на входе, коэффициенты ряда определяют­ся характеристикой нелинейного устройства.

Преобразование Лапласа некоторых видов характеристик нели­нейных устройств приведены в табл. 22.1. Там же даны выражения для соответствующих коэффициентов разложения h_n. Расширени­ем табл. 22.1 является таблица в [20].

Спектральная плотность мощности случайного процесса на вы­ходе устройства определяется преобразованием Фурье его корре­ляционной функции.

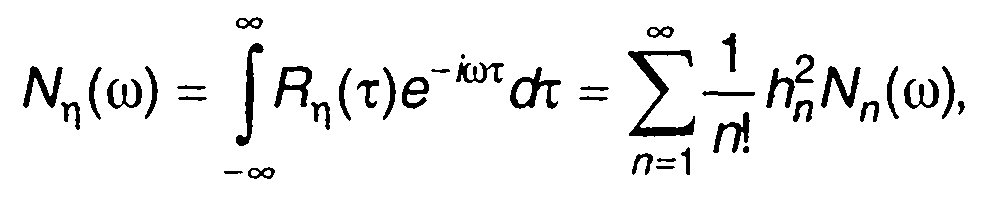(22.89)

где

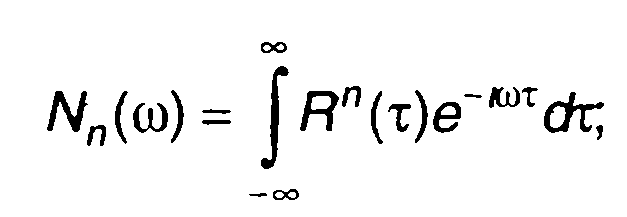
R(т) - корреляционная функция случайного процесса на входе.

Рассмотрим примеры использования метода преобразований при получении характеристик случайного процесса на выходе не­линейного устройства со степенной характеристикой и идеального ограничителя.

66 5

22.3.2. Нелинейные устройства с односторонней степенной характеристикой

Характеристика нелинейного преобразователя имеет вид

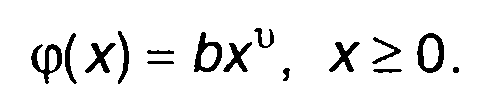(22.90)

Преобразование Лапласа (22.90):

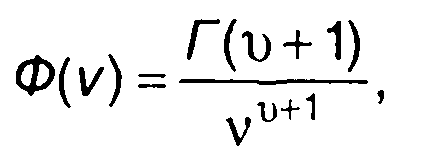(22.91)

где Г(х) - гамма-функция.

Таблица 22.1

Характеристики нелинейных устройств.

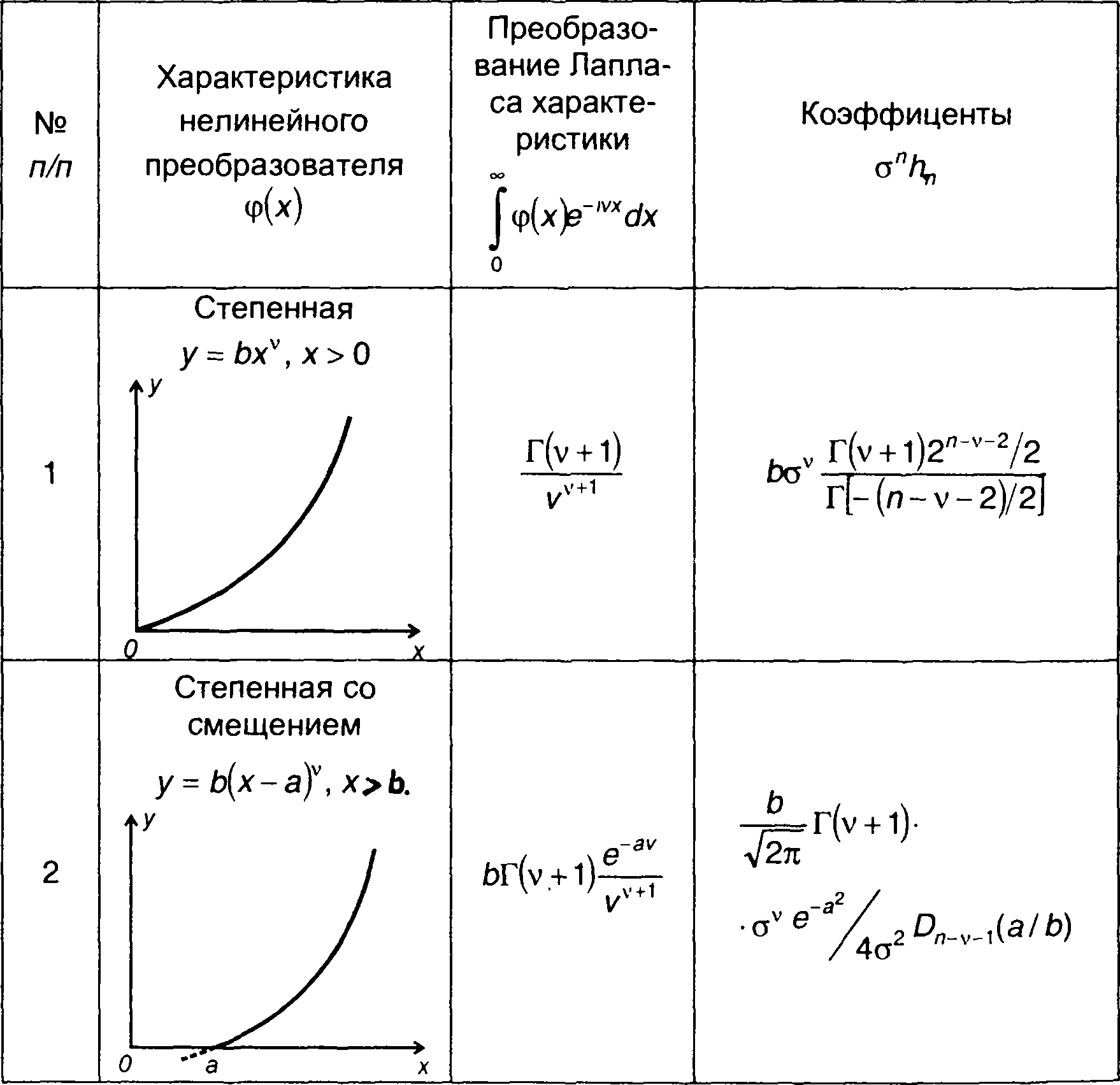
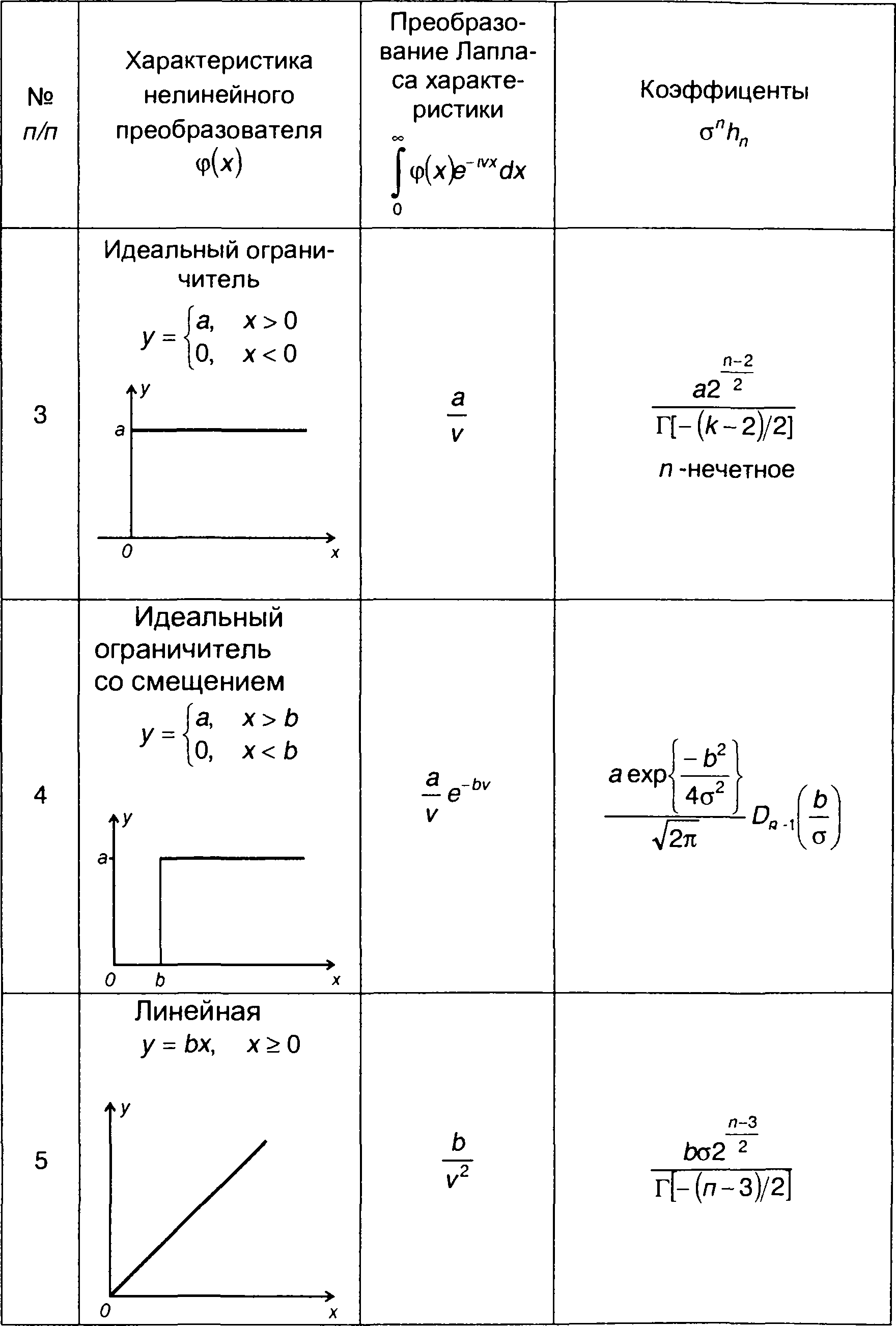
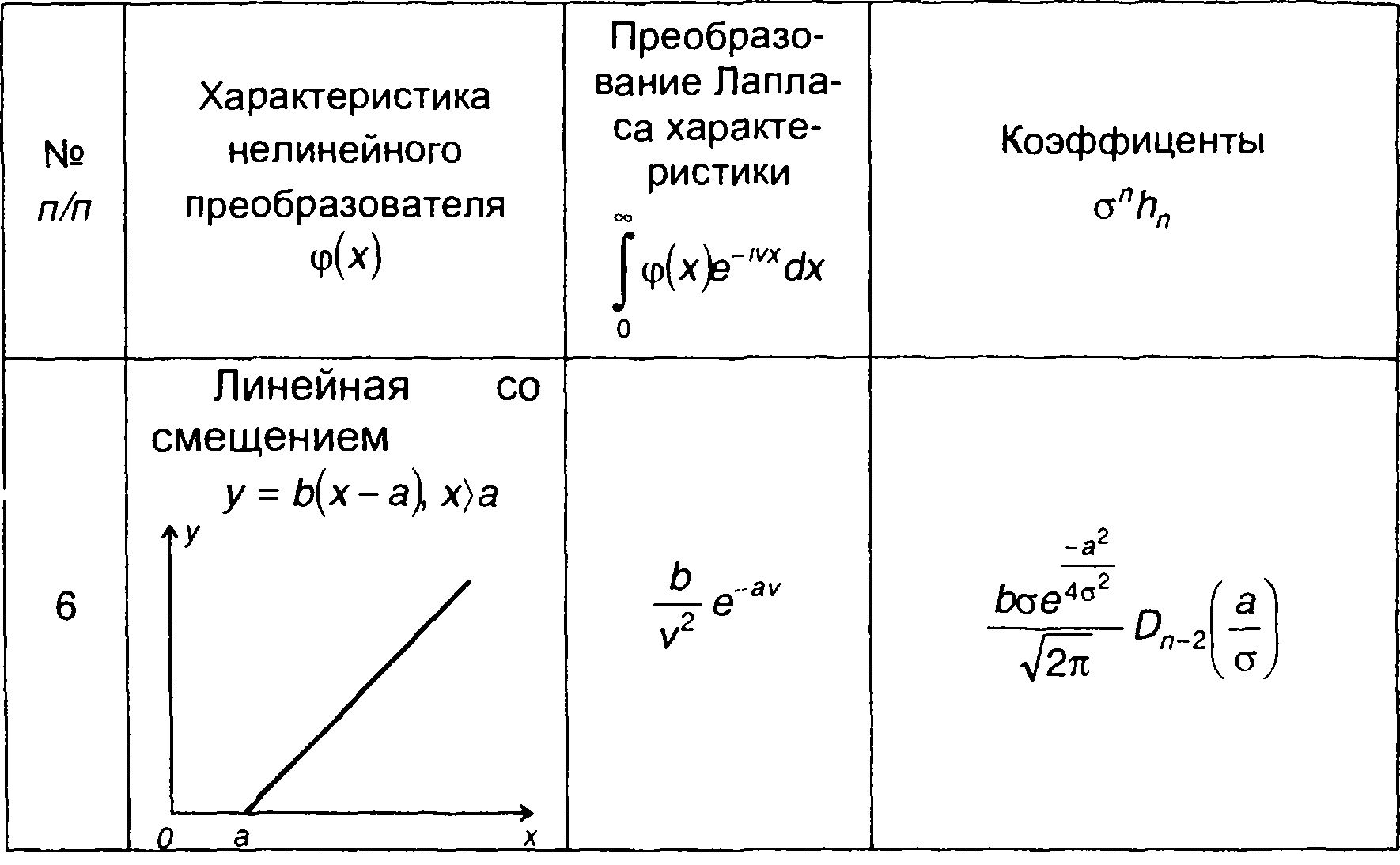
Примечание: Г(х) - гамма-функция; D(x) - функция Вебера, D_n(x)= е^-x(2/4) Н_n(х) Н(х) - многочлен Эрмита.

С учетом (22.91) из (22.88) найдем

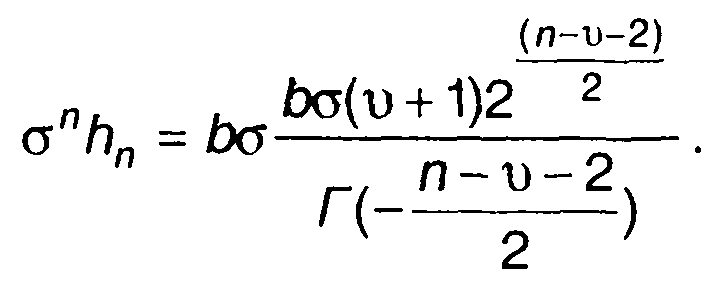(22.92)

При v = 1 из (22.87) с учетом (22.92) получим

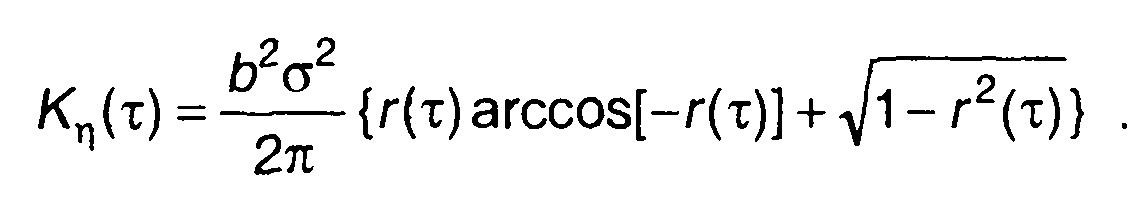(22.93)

Выражение (22.93) совпадает с полученным ранее прямым ме­тодом (22.32).

22.3.3. Идеальный ограничитель

Характеристика ограничителя имеет вид

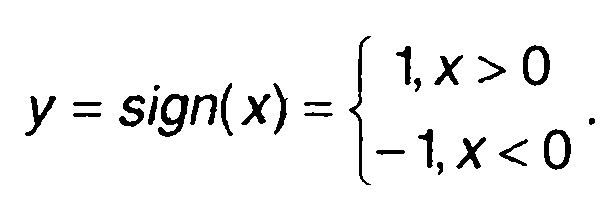(22.94)

Преобразование Лапласа характеристики

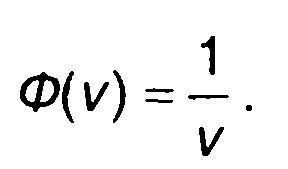(22.95)

Для центрированного гауссовского процесса на входе выраже­ние (22.87) принимает вид

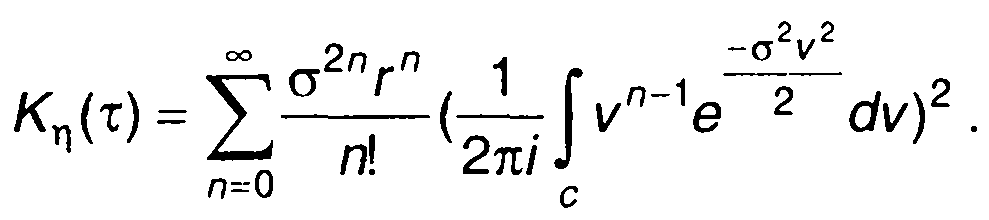(22.96)

Из (22.96) после ряда преобразований можно получить сле­дующее выражение для ковариационной функции случайного про­цесса на выходе

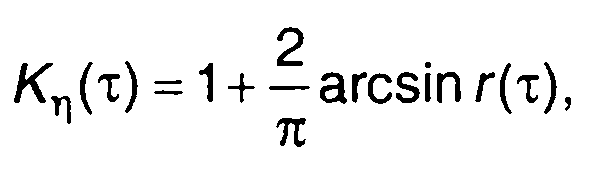(22.97)

где r(т) - нормированная корреляционная функция случайного процесса на входе идеального ограничителя.

Корреляционная функция случайного процесса на выходе иде­ального ограничителя описывается выражением

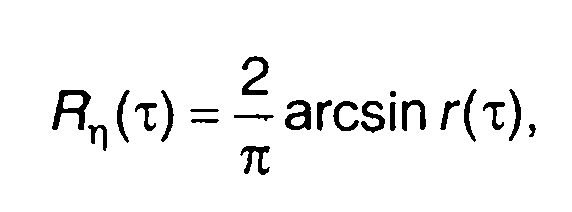(22.98)

соответствующая спектральная плотность мощности:

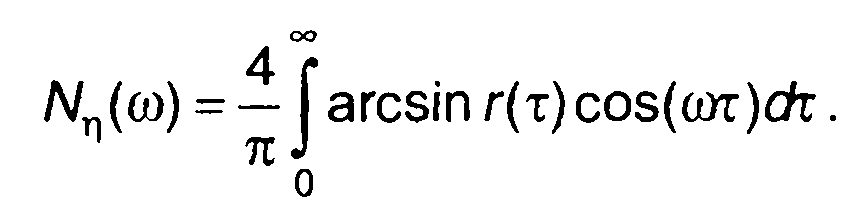
22.4. Метод производных

Если случайный процесс на входе нелинейного устройства яв­ляется гауссовским, в ряде случаев появляется возможность упро­стить операции получения корреляционной функции случайного сигнала на выходе.

Упрощения связаны с использованием выражений для произ­водных ковариационной функции случайного процесса на выходе устройства исходя из нормированной корреляционной функции случайного процесса на входе.

22.4.1. Производные корреляционной функции случайного процесса на выходе нелинейного элемента

При подаче на вход нелинейного устройства гауссовского про­цесса ξ(t) выражение для ковариационной функции случайного процесса на выходе η(t) (22.84) имеет вид

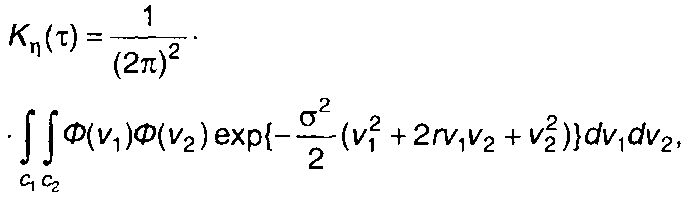(22.99)

где σ², r(т) - дисперсия и нормированная корреляционная функция случайного процесса на входе.

Дифференцирование (22.99) по г(т) дает следующее выраже­ние

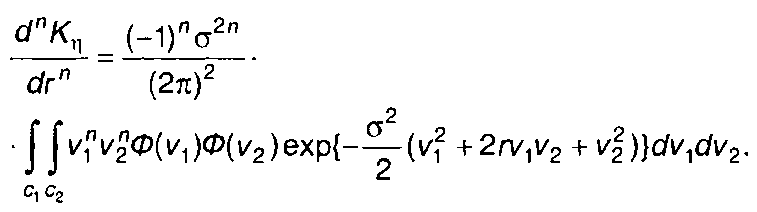(22.100)

Подставляя вместо двумерной характеристической функции га­уссовского процесса в (22.100) ее определение через ПРВ

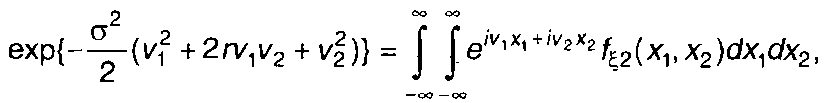
запишем

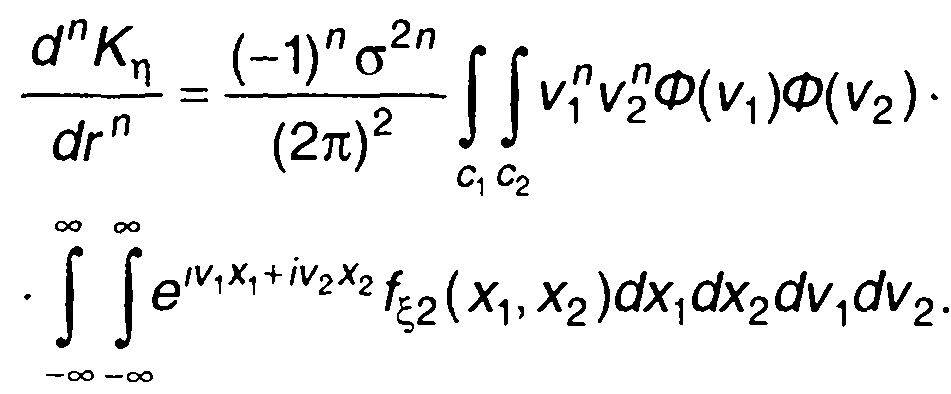(22.101)

В (22.101) переменные интегрирования v, и v₂ разделяются. Для каждого интеграла имеет место следующее равенство

Нелинейные преобразования случайных процессов

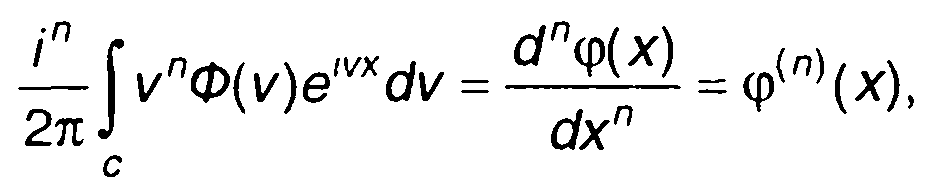(22.102)

где φ(х) - характеристика нелинейного устройства.

Это равенство получается при дифференцировании (22.81). С учетом (22.102) из (22.101) получим

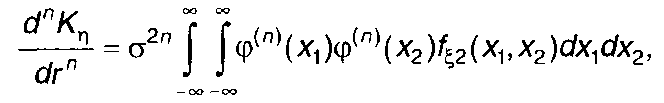(22.103)

где f_ξ2(x₁,x₂) - двумерная ПРВ гауссовского процесса на входе.

Записанное соотношение позволяет получить производную кор­реляционной функции на выходе нелинейного устройства, удобно в том случае, когда имеется достаточно простое решение двойного интеграла (22.103). Такое решение получается, в частности, в том случае, когда характеристика нелинейного элемента представляет многочлен и решение интеграла в (22.103) становится очевидным. Нелинейные устройства с такой характеристикой и рассматрива­ются в качестве примеров.

22.4.2. Односторонняя линейная характеристика

Характеристика нелинейного устройства имеет вид

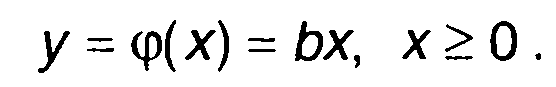(22.104)

Вторая производная (22.104) представляет импульсную функцию

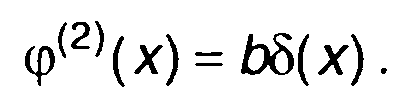(22.105)

Подставляя (22.105) в (22.103), получим

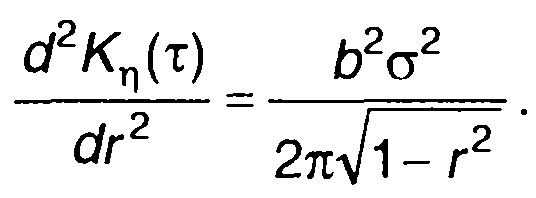(22.106)

Решение (22.106) с учетом начальных условий при r = 0

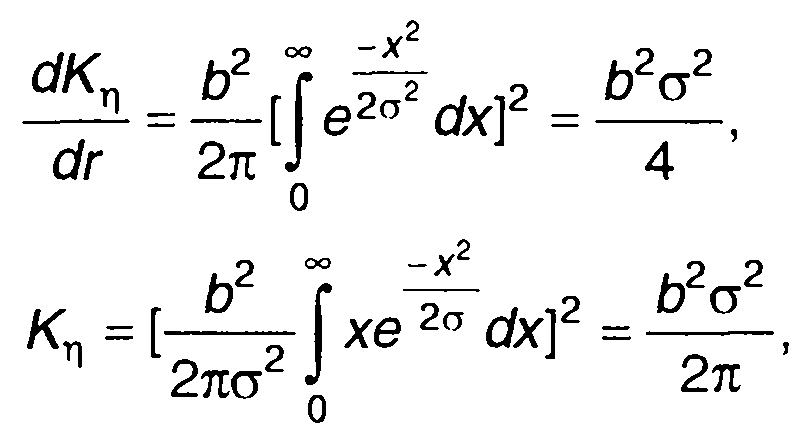(22.107)

дает

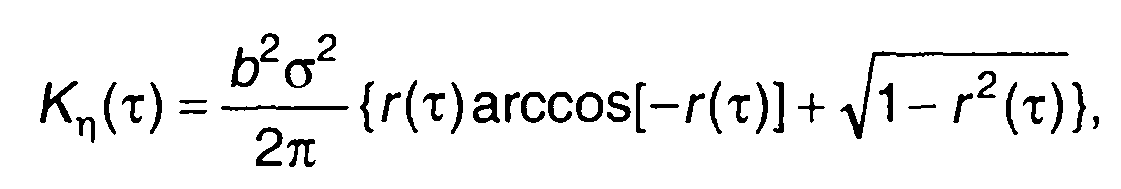(22.108)

что совпадает с (22.30).

22.4.3. Односторонняя квадратичная характеристика

Характеристика нелинейного устройства имеет вид

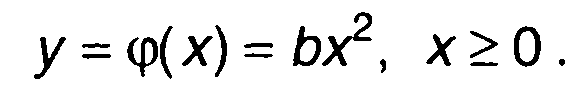(22.109)

Для такой характеристики

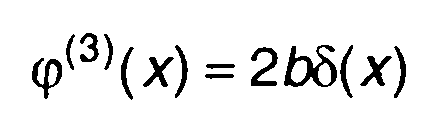(22.110)

из (22.103) получим

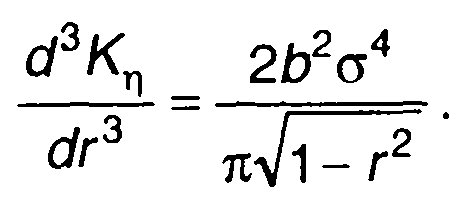(22.111)

Начальные условия при r = 0

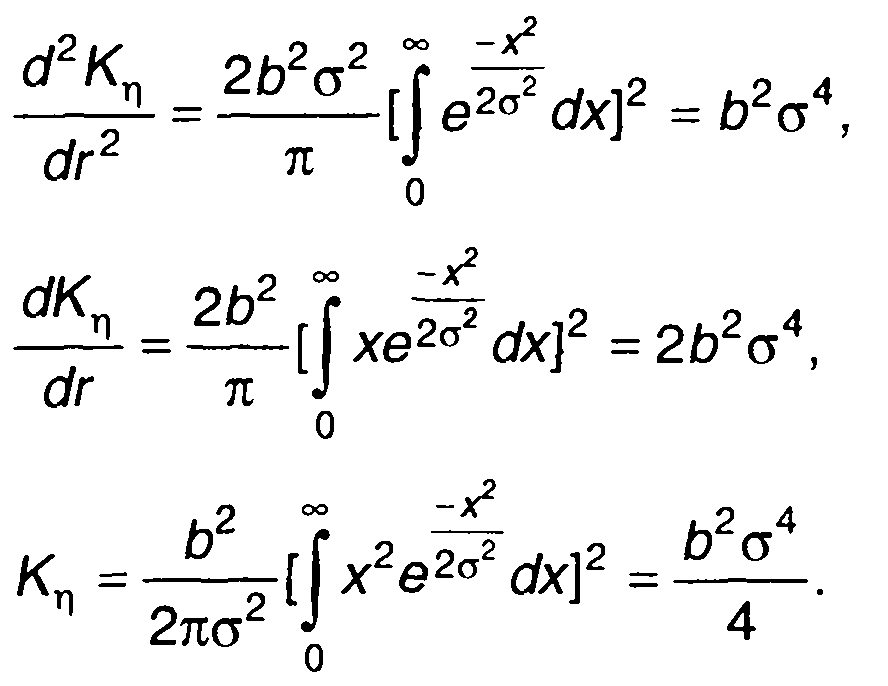(22.112)

Из (22.111) с учетом (22.112) получим

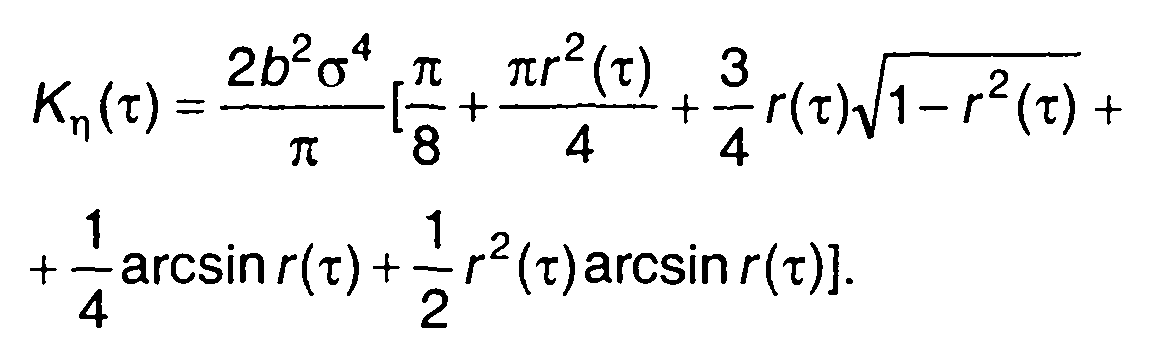(22.113)

22.4.4. Идеальный ограничитель

Характеристика идеального ограничителя имеет вид

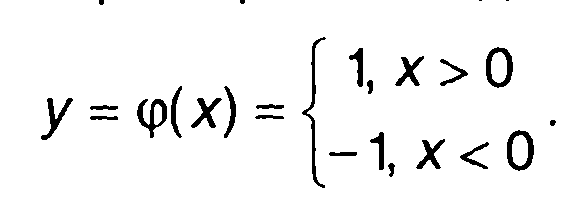(22.114)

Для такой характеристики получим

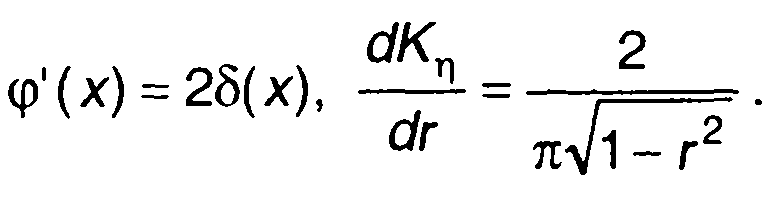(22.115)

Начальные условия при

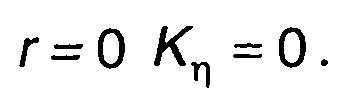(22.116)

Из (22.115) с учетом (22.116) находим

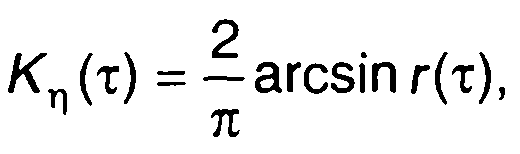(22.117)

что совпадает с (22.98) результатом, полученным методом преобразо­ваний.

Раздел 23.

АНАЛИЗ ХАРАКТЕРИСТИК СЛУЧАЙНОГО ПРОЦЕССА НА ВЫХОДЕ МНОЖИТЕЛЬНОГО КОРРЕЛЯТОРА

Широкое применение корреляторов, в первую очередь при об­наружении сигналов и измерении характеристик сигналов и шумов, обуславливает практический интерес к их анализу. С другой сторо­ны, рассмотрение случайного процесса на выходе коррелятора является хорошей иллюстрацией применения методов анализа случайных процессов и прежде всего их линейных и нелинейных преобразований в практике исследований.

В разделе проводится анализ случайного процесса на выходе множительного коррелятора, представляющего последовательно соединенные перемножитель и фильтр, на одном из входов пере- множителя включена линия задержки (рис. 23.1).

23.1. Распределение случайного процесса на выходе перемножителя

Случайный процесс на выходе перемножителя η(t) представля­ет результат перемножения случайного процесса ξ(t) с его копией после задержки на интервал времени Г (рис. 23.1)

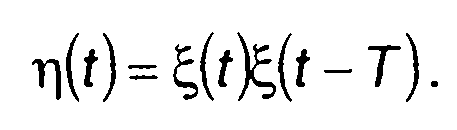(23.1)

Зная двумерную ПРВ случайных величин ξ(t) и ξ(t-T) - f_ξ2(x₁,x₂), можно определить ПРВ их произведения η(t).

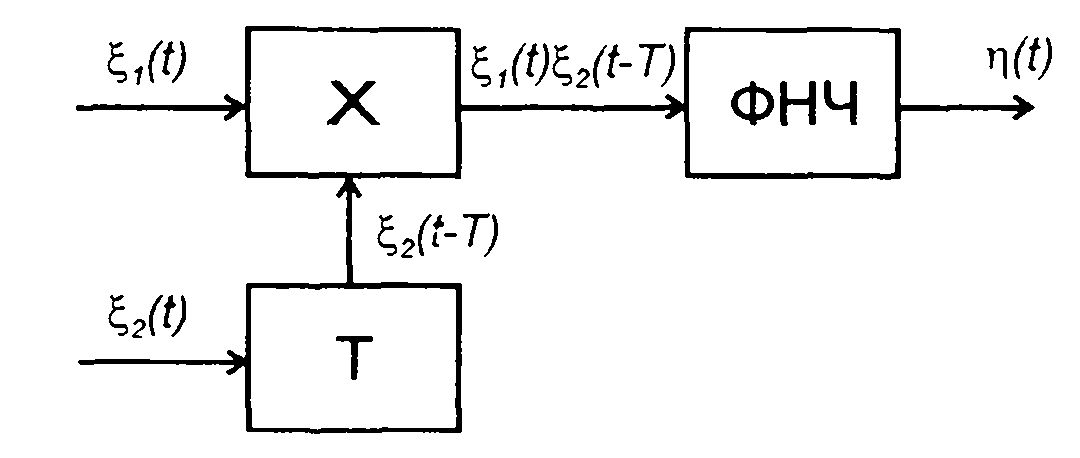
Рис. 23.1

Используя результаты, полученные в разд. 17, для ПРВ случай­ного процесса η(t) запишем следующее выражение

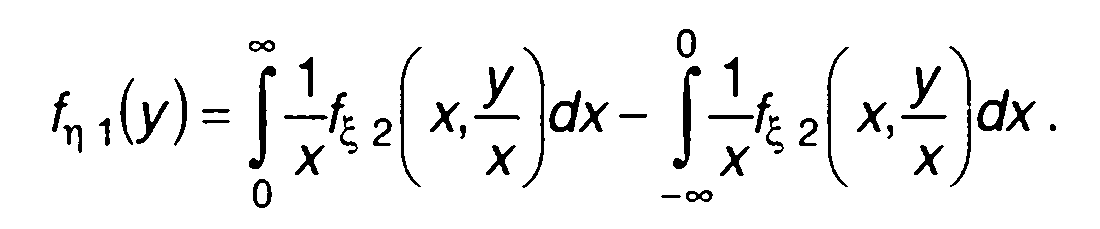(23.2)

В дальнейшем будем рассматривать ξ(t) как центрированный га­уссовский процесс. Это наиболее часто встречающийся на практике случай. Для гауссовского процесса ξ(t), имеющего двумерную ПРВ

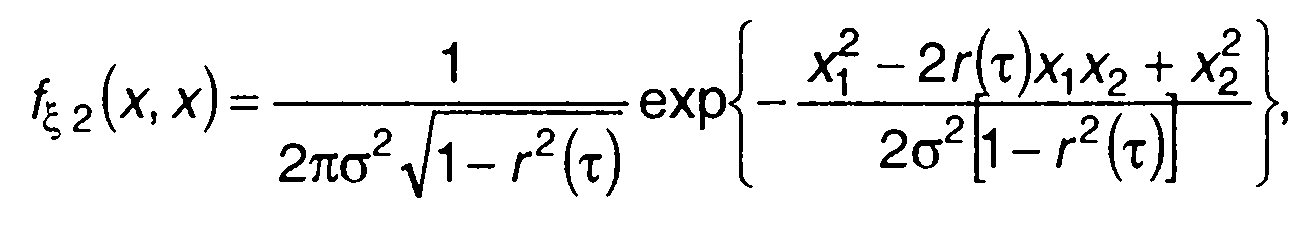(23.3)

где σ², r(τ) - дисперсия и нормированная корреляционная функ­ция ξ(t),

выражение (23.2) примет вид

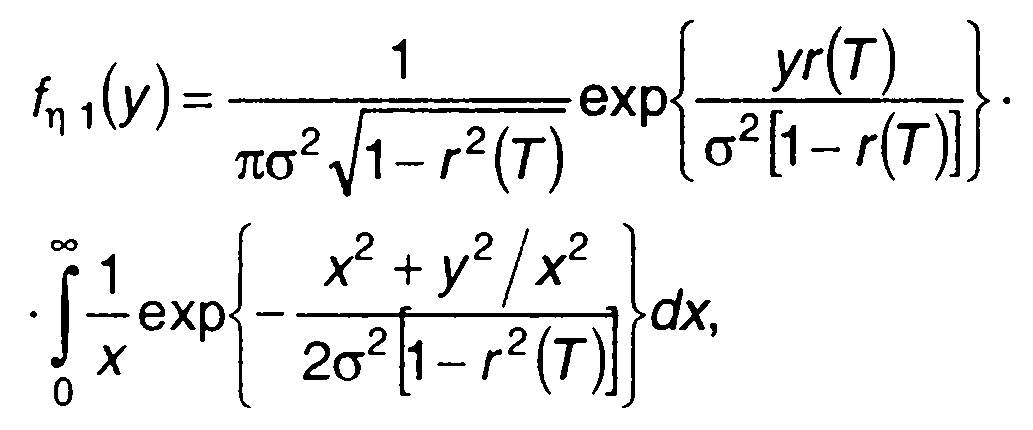(23.4)

где Т- задержка на входе коррелятора.

Решая (23.4), получаем

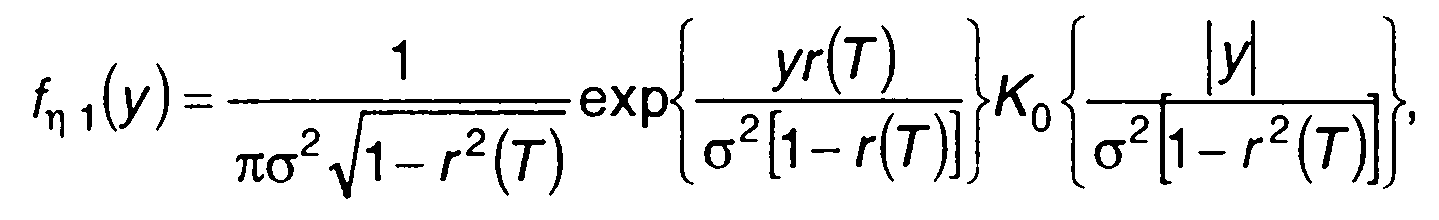(23.5)

где K₀(x) - модифицированная функция Бесселя.

Графики ПРВ случайного процесса на выходе перемножителя приведены на рис. 23.2.

23.2. Корреляционная функция и спектр случайного процесса на выходе перемножителя

Математическое ожидание случайного процесса на выходе пе­ремножителя η(t) равно

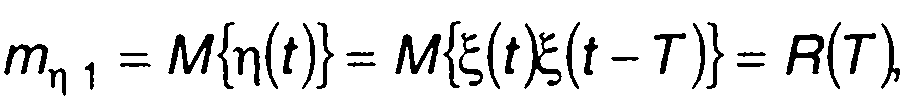(23.6)

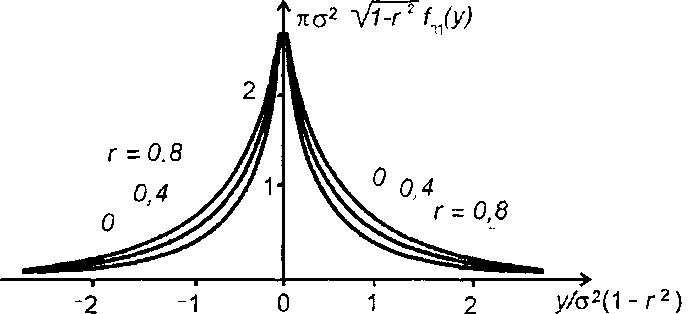
Рис. 23.2

где R(T) - корреляционная функция случайного процесса на входе ξ(t); Т - задержка случайного процесса на одном из входов пере- множителя.

Как следует из (23.6), постоянная составляющая на выходе перемножителя является несмещенной оценкой корреляционной функции случайного процесса ξ(t).

На постоянную составляющую накладываются флуктуации, ко­торые представляют источник ошибок измерения корреляционной функции (рис. 23.3).

Второй начальный момент случайного процесса на выходе перемножителя (ковариационная функция) определяется моментом четвертого порядка случайного процесса на входе

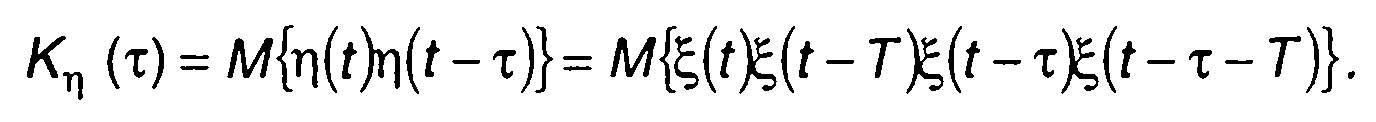(23.7)

Для гауссовского процесса 4(0 имеет место следующее равен­ство

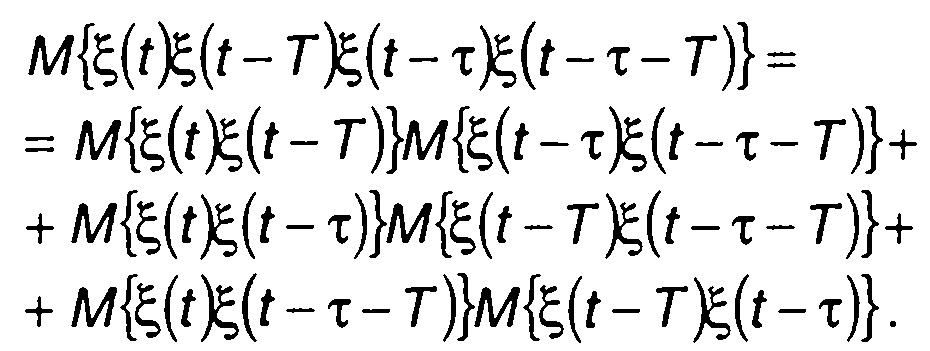(23.8)

Таким образом, выражение для ковариационной функции слу­чайного процесса на выходе перемножителя запишется в виде

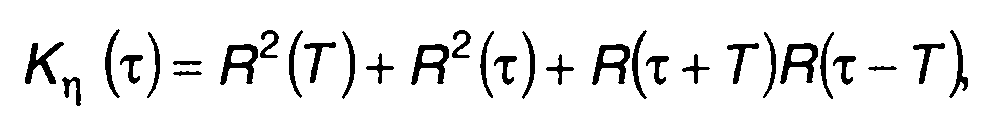(23.9)

где R(т) - корреляционная функция случайного процесса на вхо­де ξ(t).

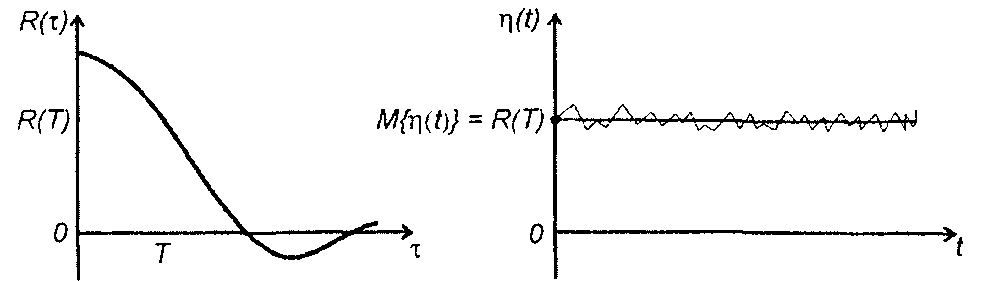
Рис. 23.3

Корреляционная функция случайного процесса η(t)

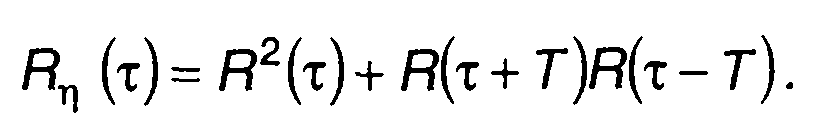(23.10)

Дисперсия η(t), характеризующая «размах» флуктуаций на вы­ходе перемножителя, определяется как

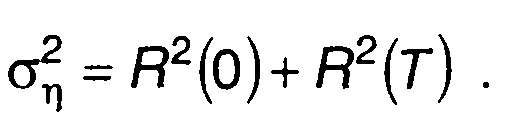(23.11)

Нормированная корреляционная функция η(t):

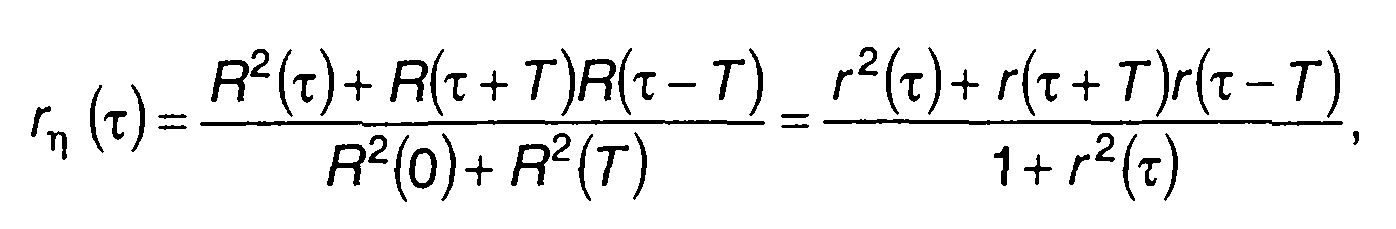(23.12)

где r(т) - нормированная корреляционная функция случайного процесса на входе ξ(t).

При Т = 0

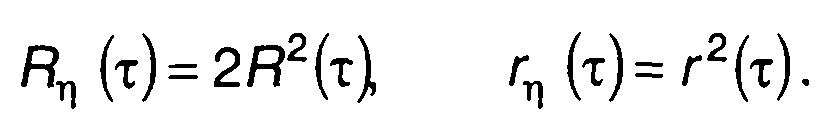(23.13)

Спектральная плотность мощности случайного процесса на вы­ходе перемножителя определяется преобразованием Фурье кор­реляционной функции R_η(т)

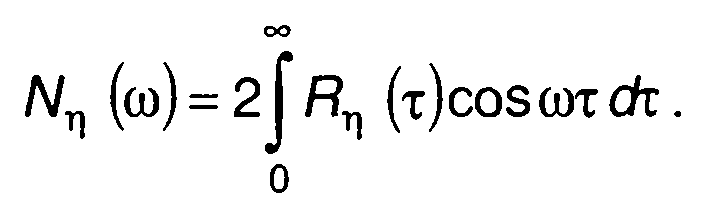(23.14)

При Т=0 выражение для N_η(ω) с учетом (23.13) можем записать

в виде свертки спектра случайного процесса на входе (свойства преобразования Фурье, разд. 3)

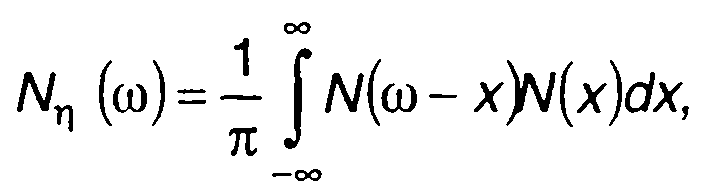(23.15)

где N(ω) - спектральная плотность мощности случайного процесса на входе ξ( t).

В качестве примера рассмотрим случайный процесс ξ(t) имеющий корреляционную функцию и спектр:

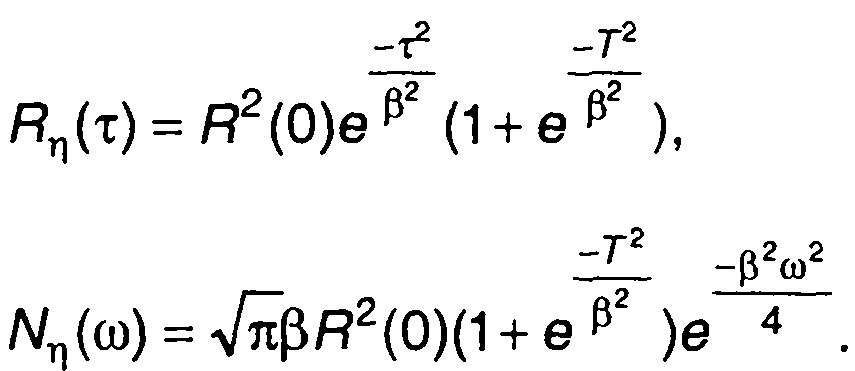
Из (23.10) и (23.14) получим (рис. 23.4)

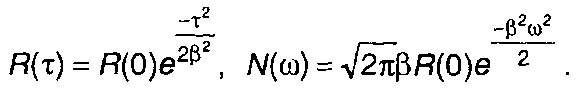
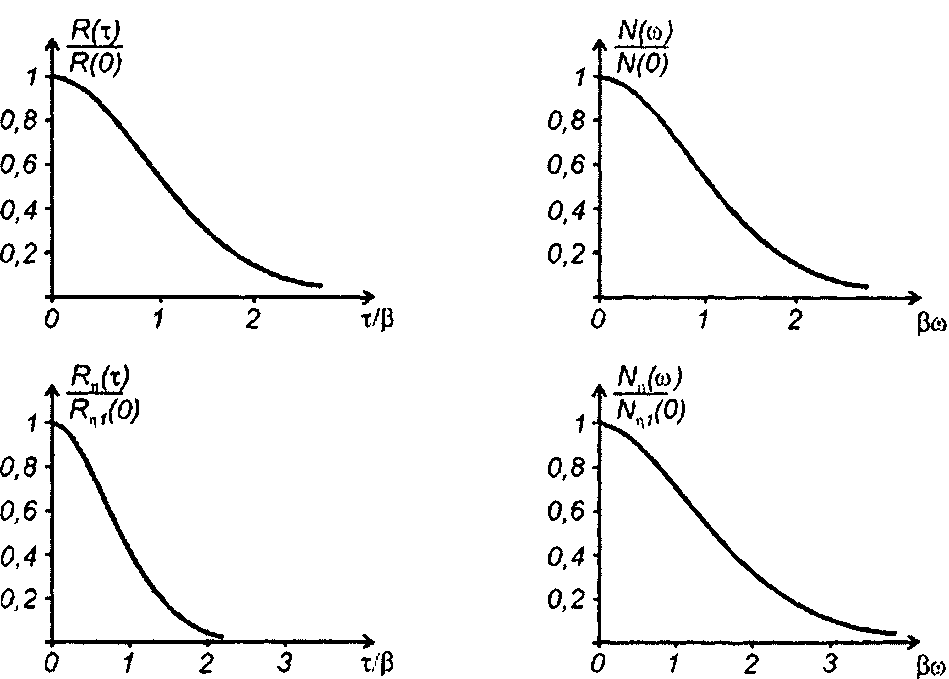
Рис. 23.4

При Т = О

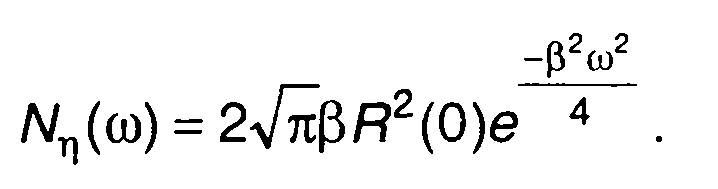
Как и следовало ожидать, корреляционная функция случайного процесса на выходе перемножителя сужается, спектр - расширя­ется.

На выходе перемножителя включен фильтр. Используя подход, описанный выше, и результаты, полученные в разд. 21, можно оп­ределить характеристики случайного процесса на выходе фильтра коррелятора.

23.3. Характеристики случайного процесса на выходе множительного коррелятора

Случайный процесс на выходе коррелятора (рис. 23.1) описы­вается выражением

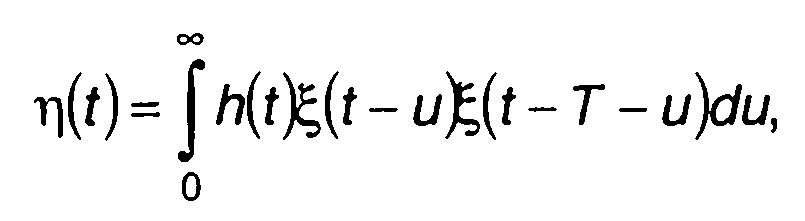(23.16)

где ξ(t) - случайный процесс на входе перемножителя; Г - за­держка на одном из входов перемножителя; h(t) - импульсная ха­рактеристика фильтра.

Как правило, ширина полосы пропускания фильтра значительно меньше ширины спектра на выходе перемножителя. Происходит нормализация случайного процесса на выходе фильтра (разд. 21). Таким образом, достаточно общим случаем, можно считать, явля­ется нормальное распределение случайного процесса на выходе коррелятора η(t); его ФРВ или ПРВ определяются математиче­ским ожиданием и корреляционной функцией случайного процесса на выходе фильтра.

Математическое ожидание случайного процесса на выходе кор­релятора равно

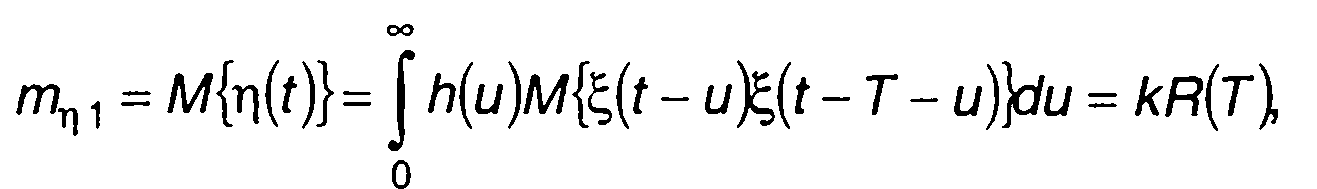(23.17)

где

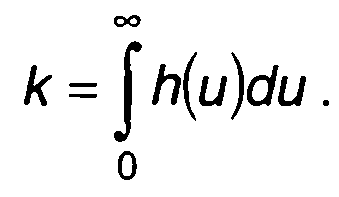
Как следует из (23.17), математическое ожидание случайного процесса на выходе коррелятора пропорционально корреляцион­ной функции случайного процесса на входе. Оно оценивается по­стоянной составляющей колебания на выходе коррелятора.

Начальный момент второго порядка случайного процесса на выходе коррелятора η(t) определяется выражением

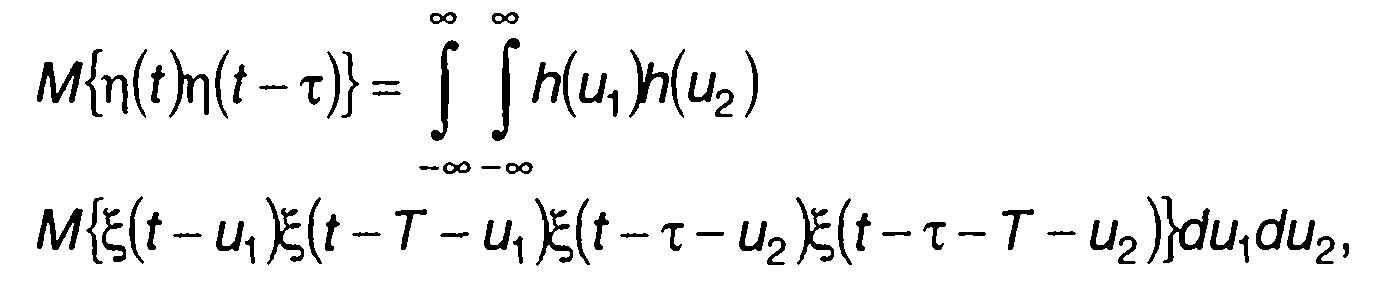(23.18)

где h(t) - определена для t≥ 0.

Для момента четвертого порядка гауссовского процесса в (23.18) запишем

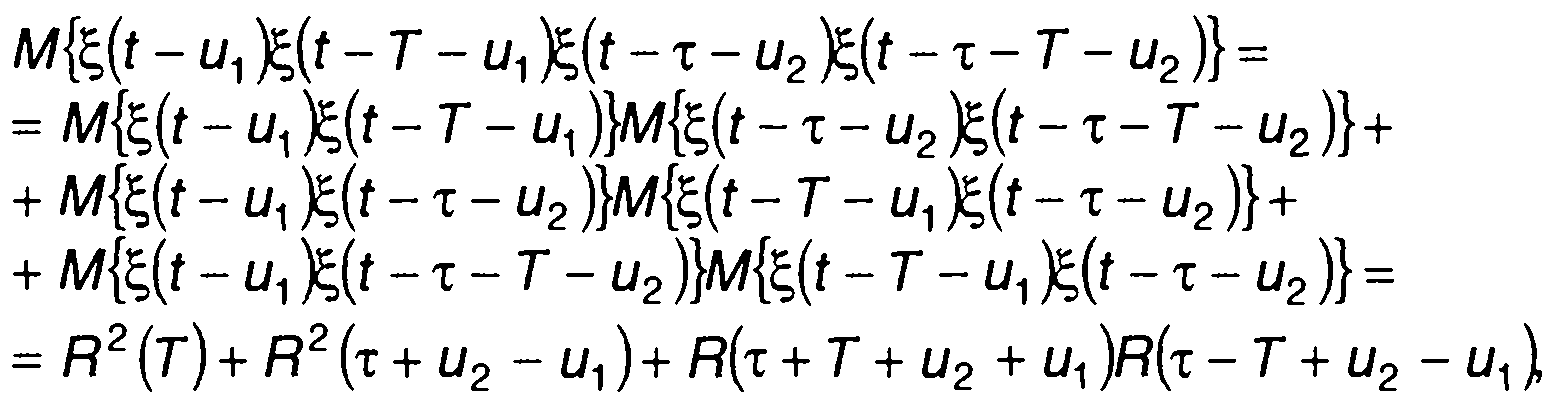(23.19)

где R(т) - корреляционная функция случайного процесса на входе

ξ(t).

Корреляционная функция случайного процесса на выходе кор­релятора определяется через начальные моменты распределения соотношением

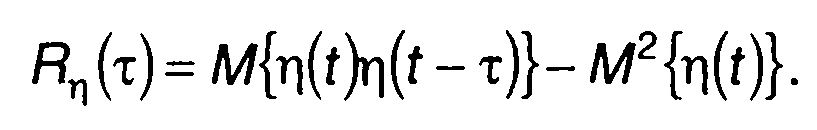(23.20)

С учетом (23.18) - (23.20) выражение для R_η(т) запишется в виде

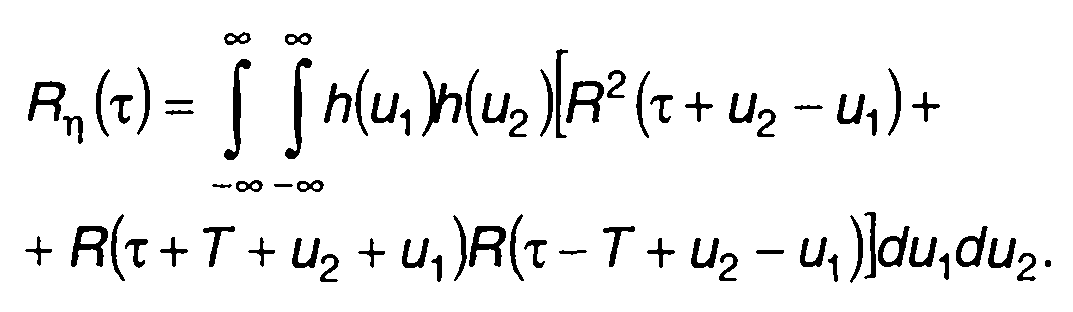(23.21)

Область интегрирования в (23.21) разобьем диагональю Перейдем от переменных и₁ и и₂ к и = и₁, v = и₂- и₁ для одной по­ловины области и к и = и₂, v = u₁- и₂ для другой. Тогда выражение для корреляционной функции случайного процесса на выходе кор­релятора получим в виде

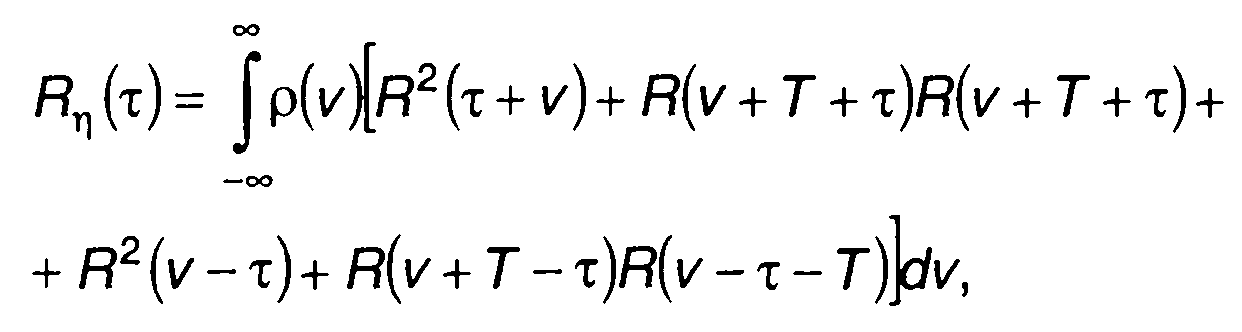(23.22)

где

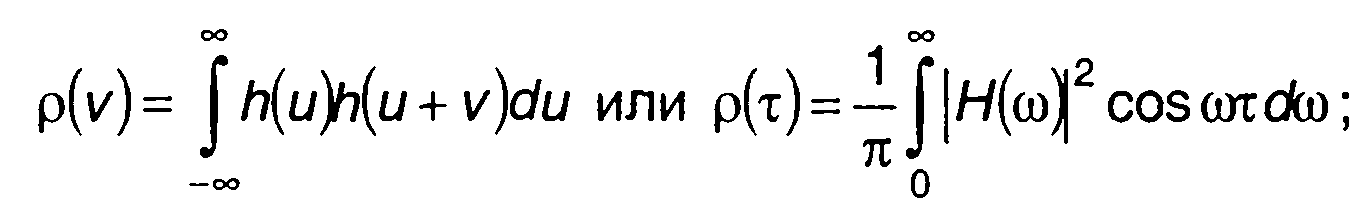
Н(ω) - частотная характеристика фильтра коррелятора.

Дисперсия случайного процесса на выходе коррелятора равна

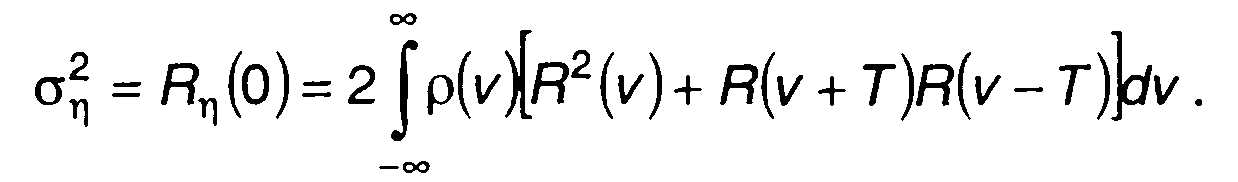(23.23)

Нормированная корреляционная функция η(t)

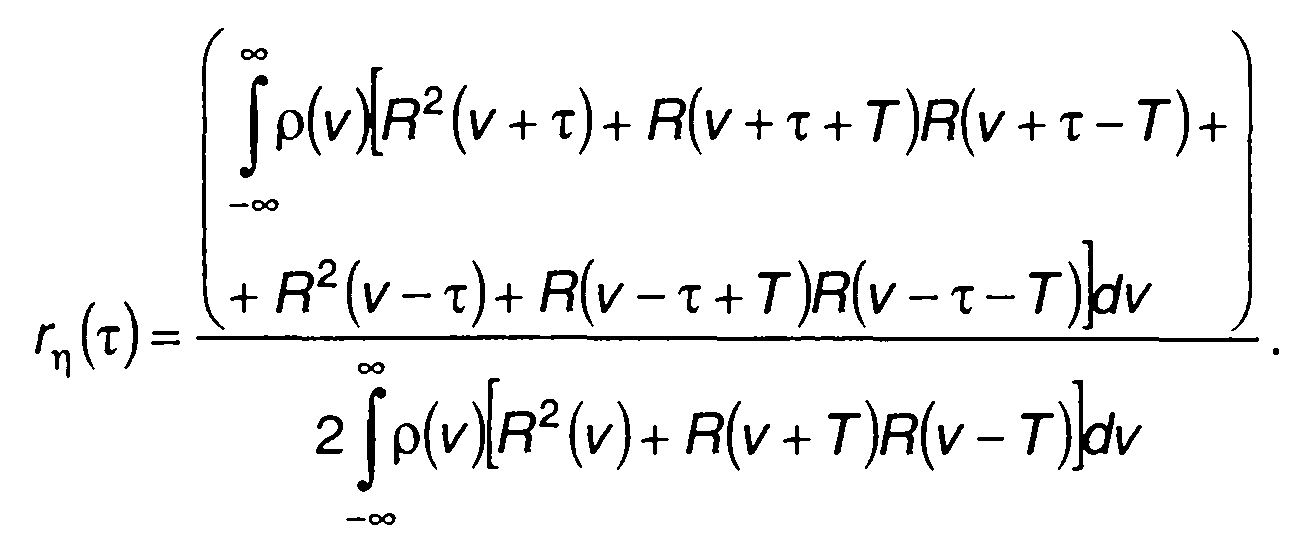(23.24)

Постоянная составляющая на выходе фильтра, как это следует из (23.17), является оценкой измеряемой корреляционной функции случайного процесса на входе ξ(t). Флуктуации, накладываемые на нее, обуславливают ошибку коррелятора. Относительная вели­чина этой ошибки может быть определена как отношение среднего квадратического отклонения случайного процесса к его математи­ческому ожиданию

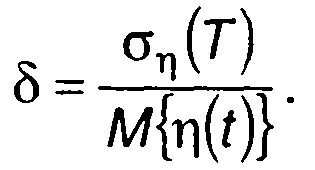(23.25)

С учетом (23.17) и (23.23) выражение для δ запишется в виде

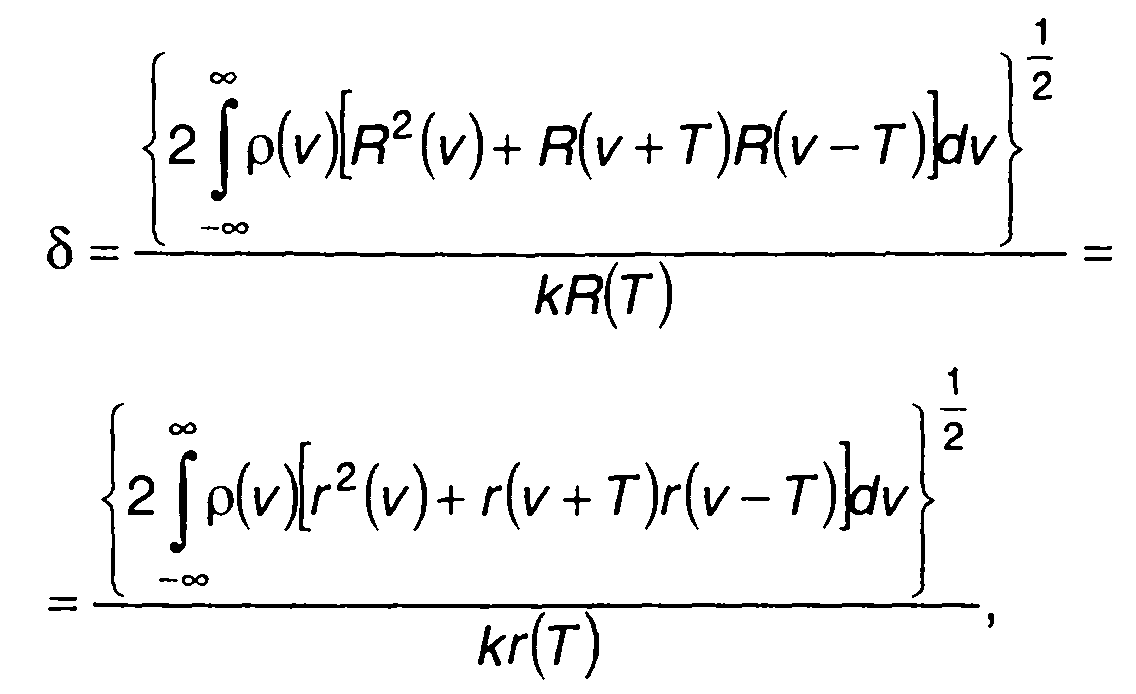(23.26)

где R(т) - корреляционная функция случайного процесса на входе; r(т) = R(т)/R(0).

Как следует из (23.26), ошибка определяется: видом и парамет­рами фильтра коррелятора, р(v); корреляционной функцией слу­чайного процесса на входе, R(т); задержкой на входе коррелятора, T.

В качестве примера рассмотрим коррелятор, содержащий фильтр, имеющий импульсную характеристику вида (например, RC- цепь)

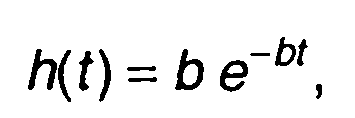
где b- постоянная величина.

Корреляционная функция случайного процесса на входе ξ(t) имеет вид

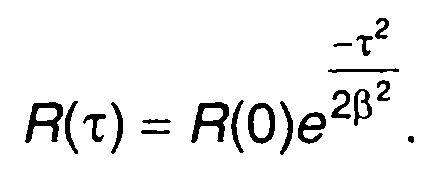
Для приведенных исходных данных из (23.22) получим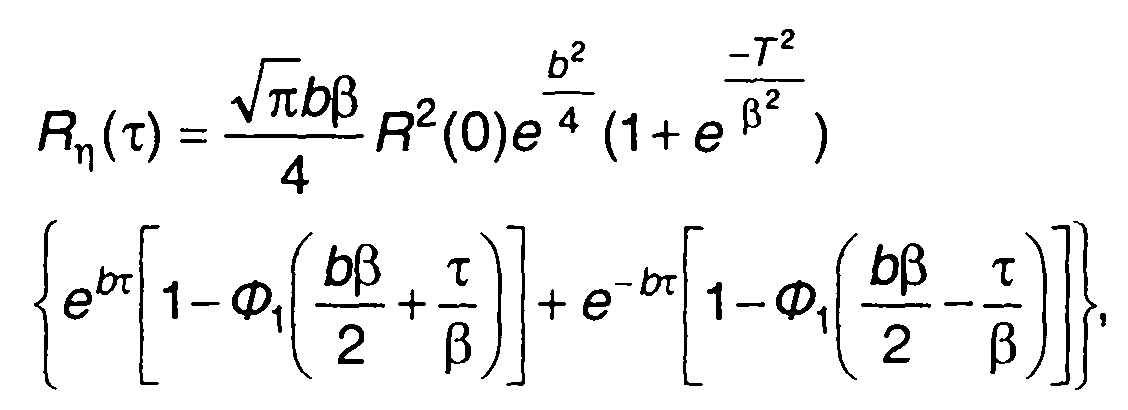

где

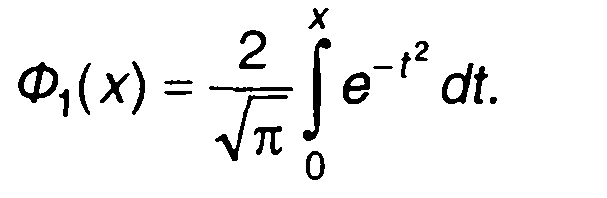
Дисперсия равна

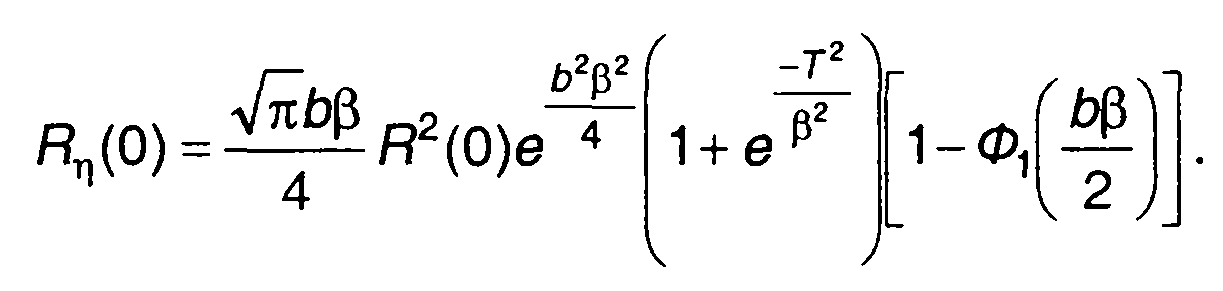
Нормированная корреляционная функция случайного процесса на выходе коррелятора

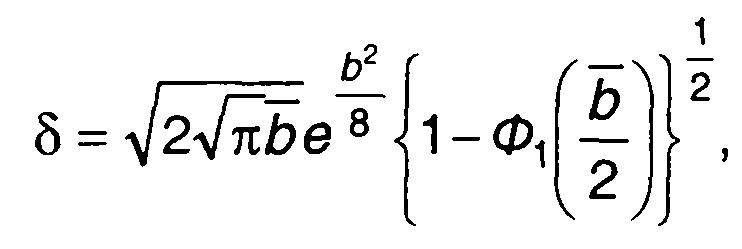
Относительная величина ошибки определяется выражением (23.26)

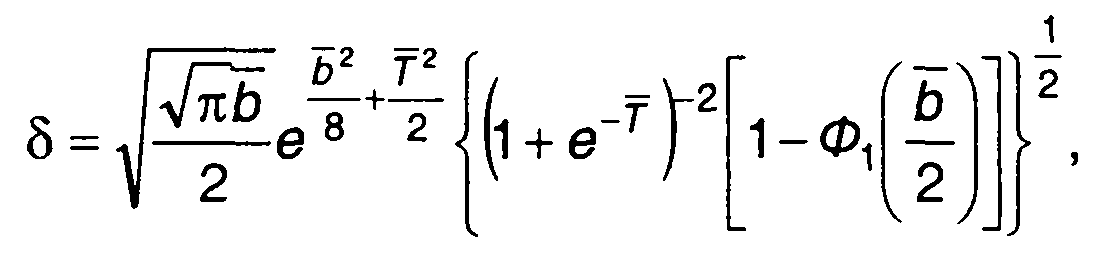
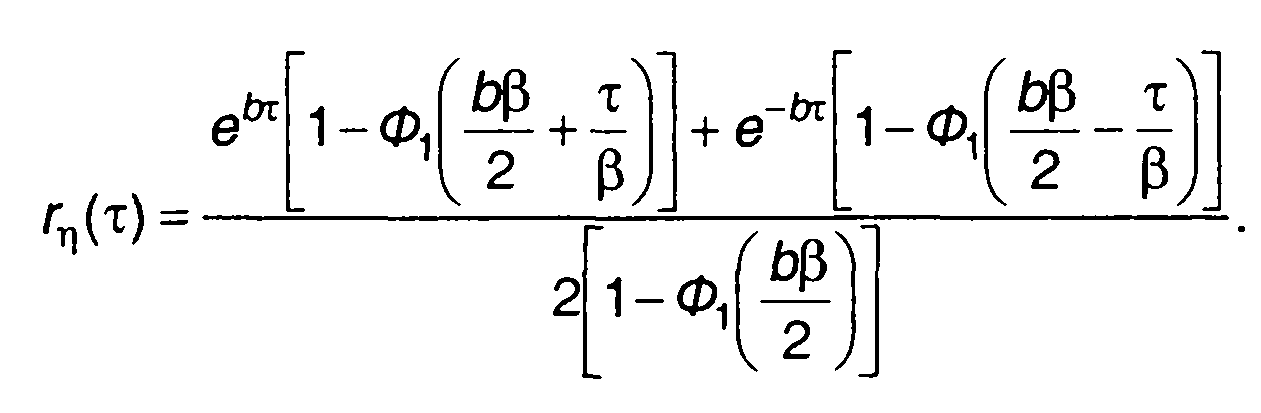
где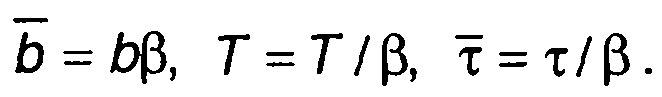

При Т – О зависит от постоянной времени фильтра 1/b и параметра корре­ляционной функции случайного процесса β, от их произведения

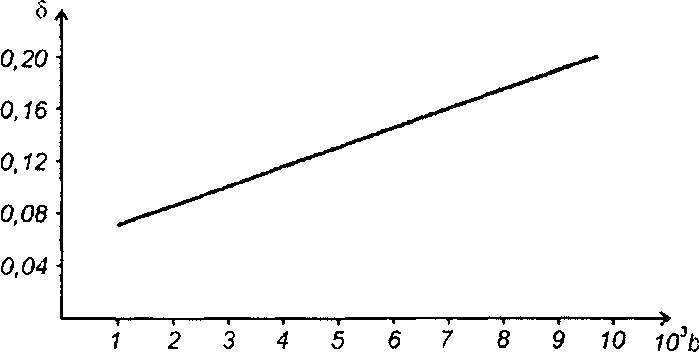
Рис. 23.5

b = bβ. На рис. 23.5 приведены графики зависимости δ от обоб­щенного параметра b в интервале значений b от 0,001 до 0,01.

При b < 0,001 можно принять δ = 1,88√b.

Принимая интервал корреляции случайного процесса на входе равным τ_к = 2,4β (R(τ_k) ≡ 0,05R(0)), можно считать, что при значе­нии постоянной времени фильтра Т = (1/ b)>500τ_к значения отно­сительной ошибки σ не превосходят 5%.

Спектральная плотность мощности случайного процесса на вы­ходе коррелятора η(t) может быть определена как преобразова­ние Фурье корреляционной функции (23.22)

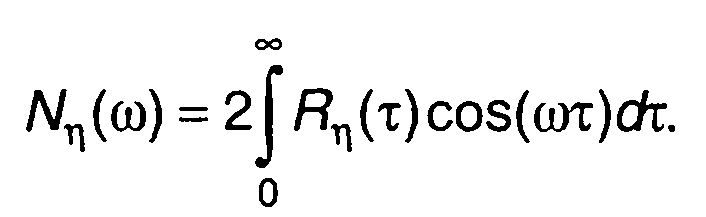
Она может быть также получена как произведение спектральной плотности мощности процесса на выходе перемножителя N_η(ω) и

квадрата модуля частотной характеристики фильтра Н(ω):

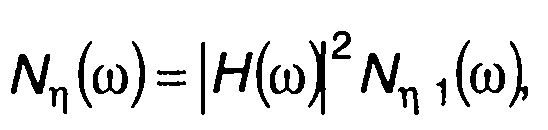(23.27)

где N_η1(ω) - спектральная плотность мощности случайного про­цесса на выходе перемножителя, определяется (23.14).

Для низкочастотного фильтра коррелятора с учетом того, что полоса пропускания фильтра значительно уже ширины спектра случайного процесса на выходе перемножителя, можно принять

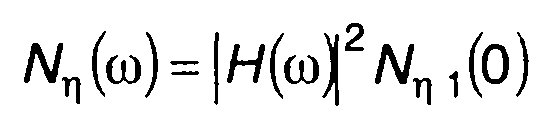(23.28)

Выражение для N_η1(0) получим из (23.14) с учетом (23.10) в виде

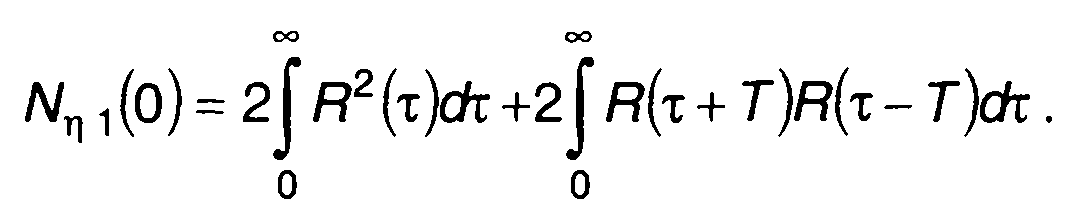(23.29)

Для условий рассмотренного выше примера получим

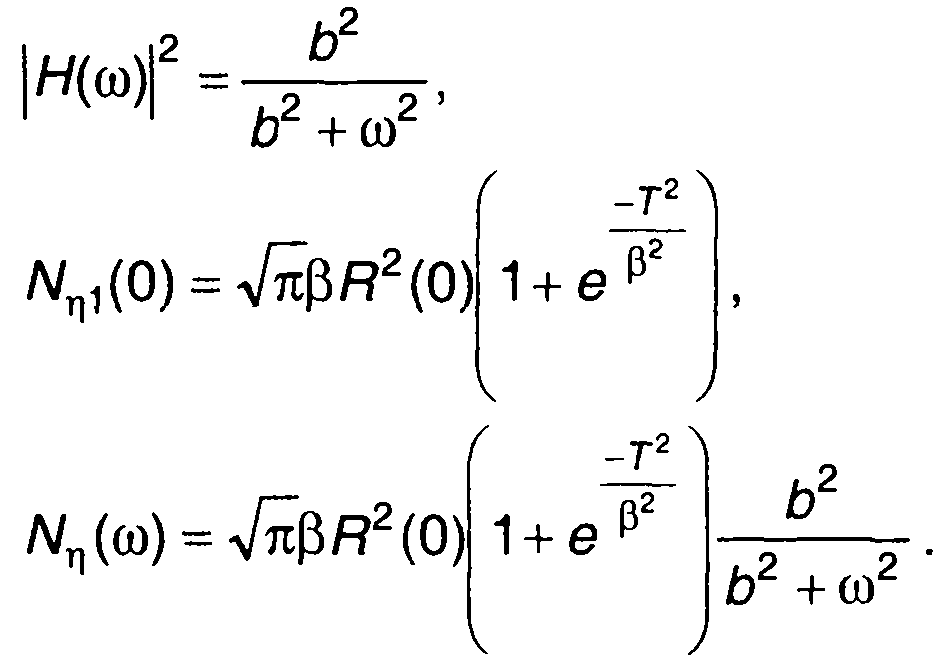
Как следует из выражения для N_η(ω), спектр случайного про­цесса на выходе коррелятора, имеющего узкополосный фильтр, определяется частотной характеристикой фильтра.

Подход к анализу случайного процесса на выходе множительно­го коррелятора может быть использован и при анализе с учетом ограниченного времени наблюдения (кратковременный анализ).

23.4. Кратковременный анализ случайного процесса на выходе множительного коррелятора

Наблюдение случайного процесса на выходе коррелятора в те­чение ограниченного интервала времени приводит к дополнитель­ным ошибкам измерения. Подход к определению этого вида оши­бок аналогичен рассмотренному в п. 23.3, что делает целесооб­разным связать материал предыдущего подраздела с оценкой ха­рактеристик случайного сигнала на выходе перемножителя и кор­релятора при кратковременном наблюдении случайного процесса.