ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 20 страница

В качестве примеров рассмотрим характеристики случайных процессов различного вида.

1. Спектральной плотности мощности, равномерной в полосе частот (рис. 18.1,а)

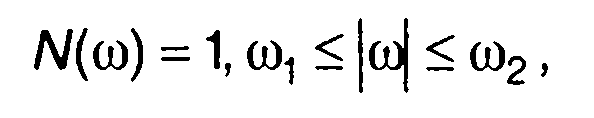
соответствует корреляционная функция случайного процесса где

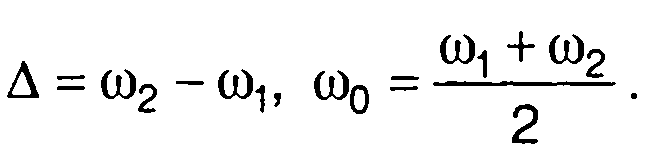
Графики r(τ) при различных соотношениях ω₁ и ω₂ приведены на рис. 18.1,6. Как следует из графиков, чем уже полоса частот, занимаемая спектром (точнее, чем меньше значение отношения ∆ω₀), тем более выражен осциллирующий характер корреляци­онной функции.

2. Спектральной плотности мощности случайного процесса (рис. 18.2,а)

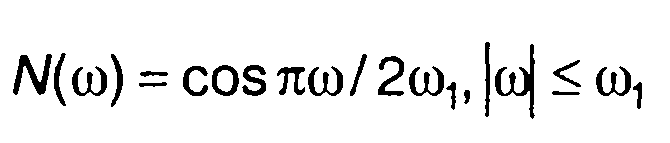
соответствует корреляционная функция (рис. 18.2,б)

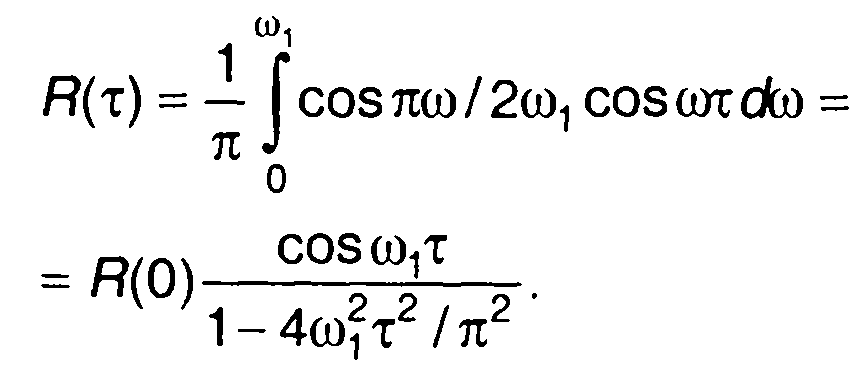
Рис. 18.1

Рис.18.2

3. Спектральной плотности мощности случайного процесса (рис. 18.3,а)

соответствует корреляционная функция (рис. 18.3,б)

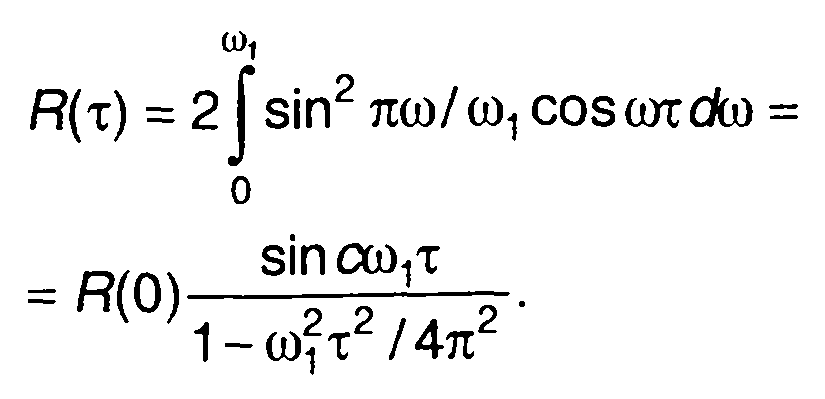
Рис. 18.3

4. Корреляционной функции случайного процесса (рис. 18.4,6) 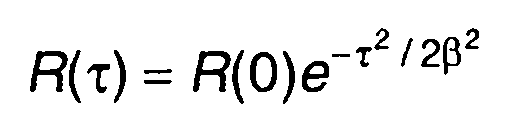соответствует спектральная плотность мощности (рис. 18.4,а)

5. Корреляционная функция телеграфного сигнала описыва­ется выражением (рис. 18.5,6)

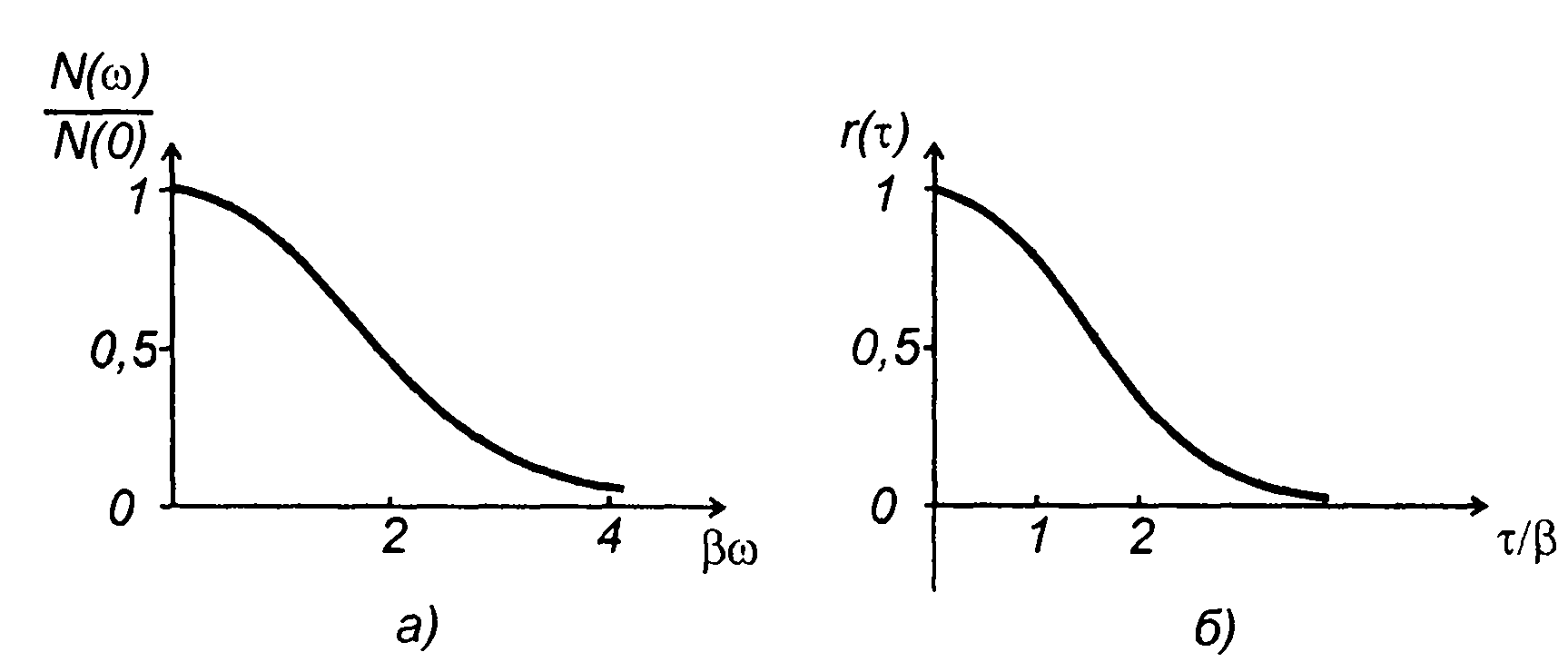
Рис. 18.4

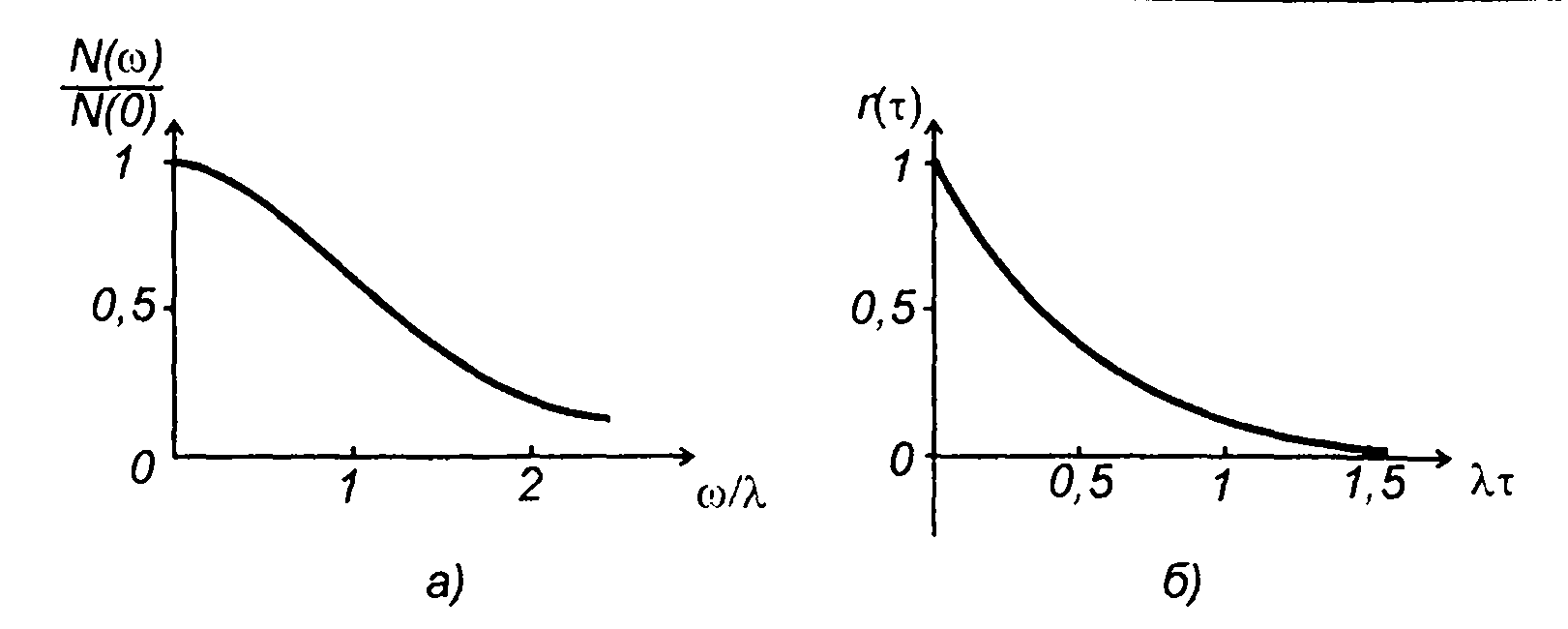
Рис. 18.5

Ей соответствует спектральная плотность мощности (рис. 18.5,а)

Число примеров спектров случайных процессов и соответст­вующих им корреляционных функций увеличивает табл. 18.1. С учетом четности функций графики N(ω) и R(т) изображены только для положительных значений ω и τ.

Условие существования преобразования Фурье, как указыва­лось, предполагает определение спектральной плотности мощно­сти только для центрированного случайного процесса. Расширить понятие спектральной плотности мощности позволяет формальный прием, основанный на определении спектральной плотности мощ­ности импульсной функции (часть 1). Преобразование Фурье им­пульсной функции определяется соотношением

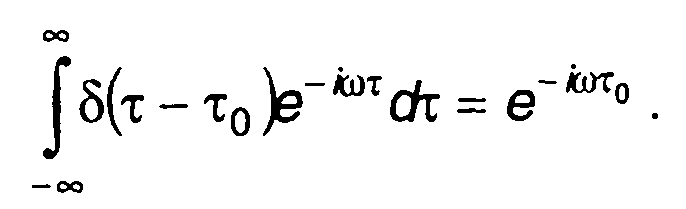(18.17)

Обратное преобразование Фурье даёт

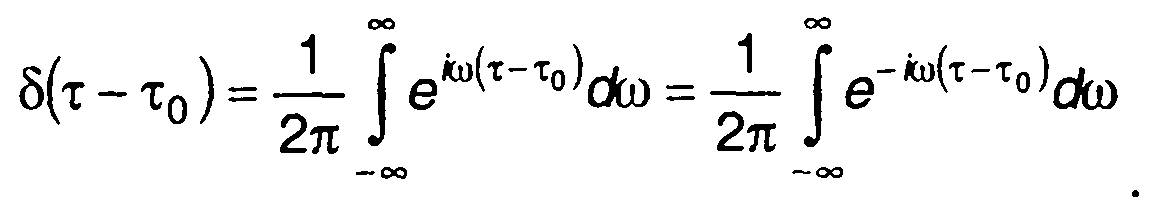(18.18)

По аналогии с (18.18) можем записать

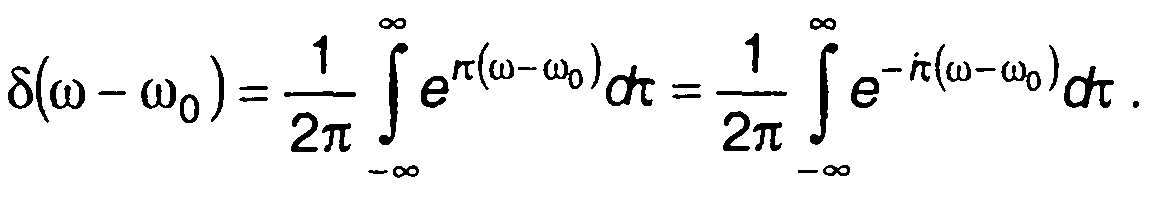(18.19)

Таблица 18.1

Спектральные плотности мощности и корреляционные функции случайных процессов

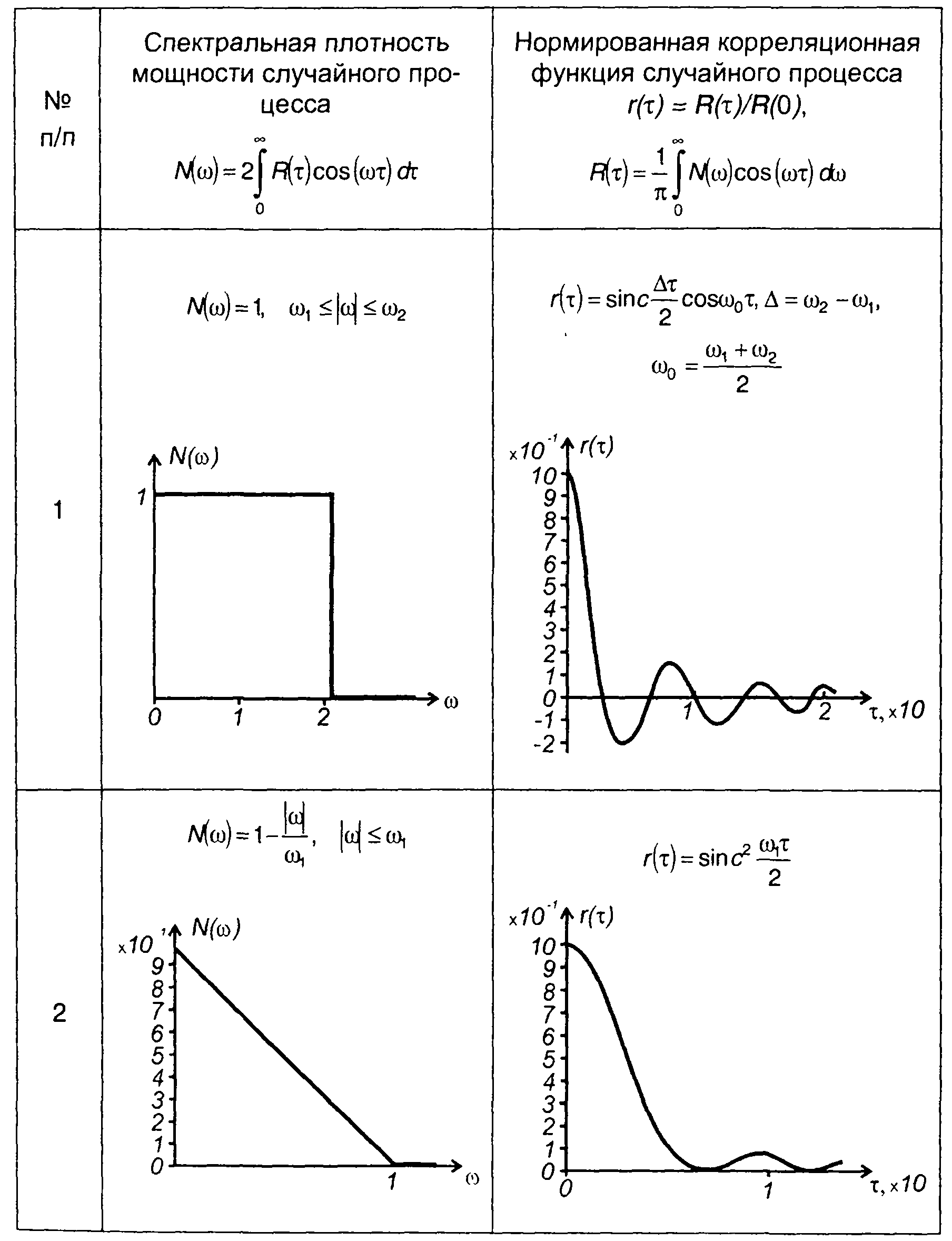
Продолжение таблицы 18.1

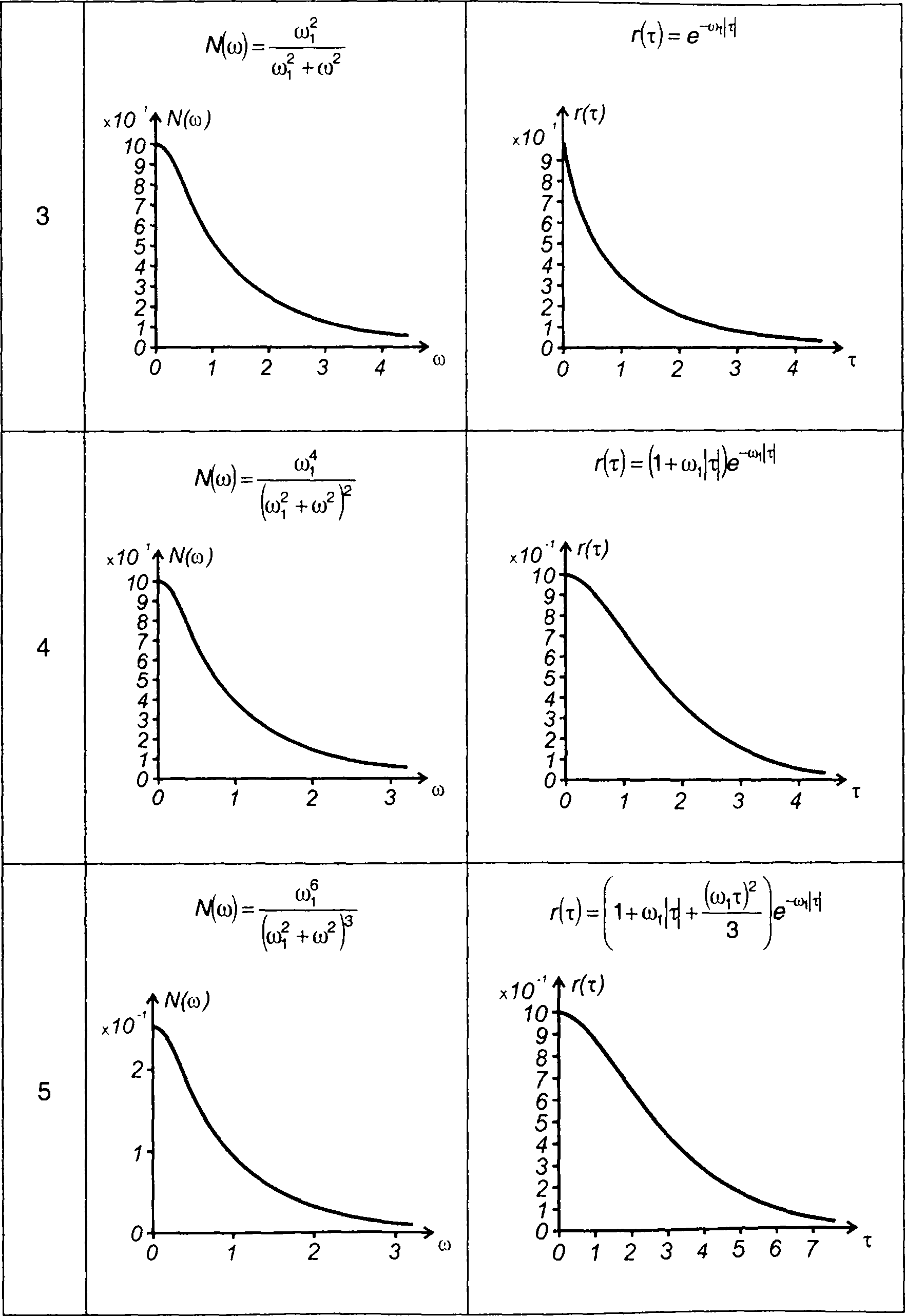
Продолжение таблицы 18.1

Продолжение таблицы 18.1

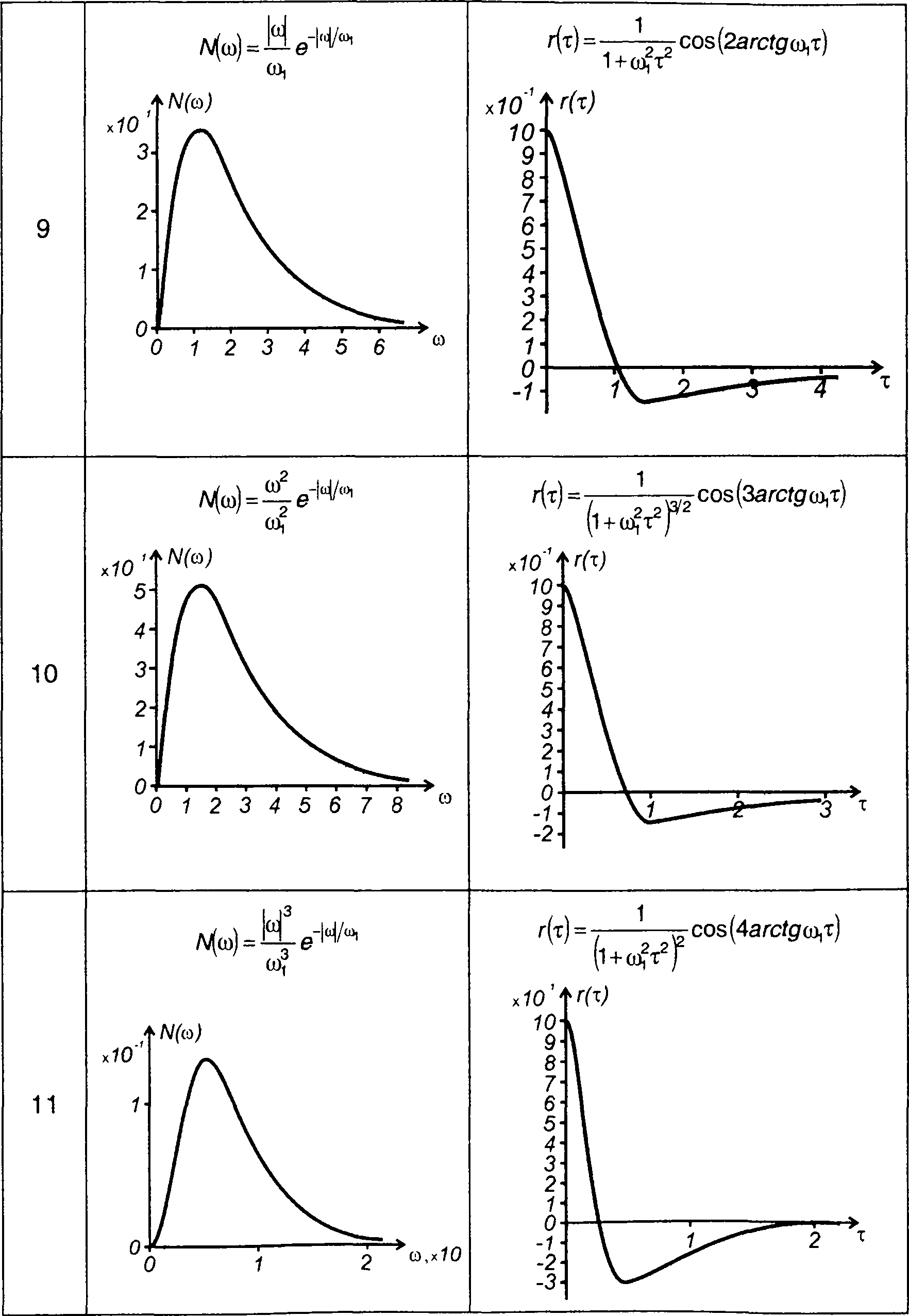
Продолжение таблицы 18.1

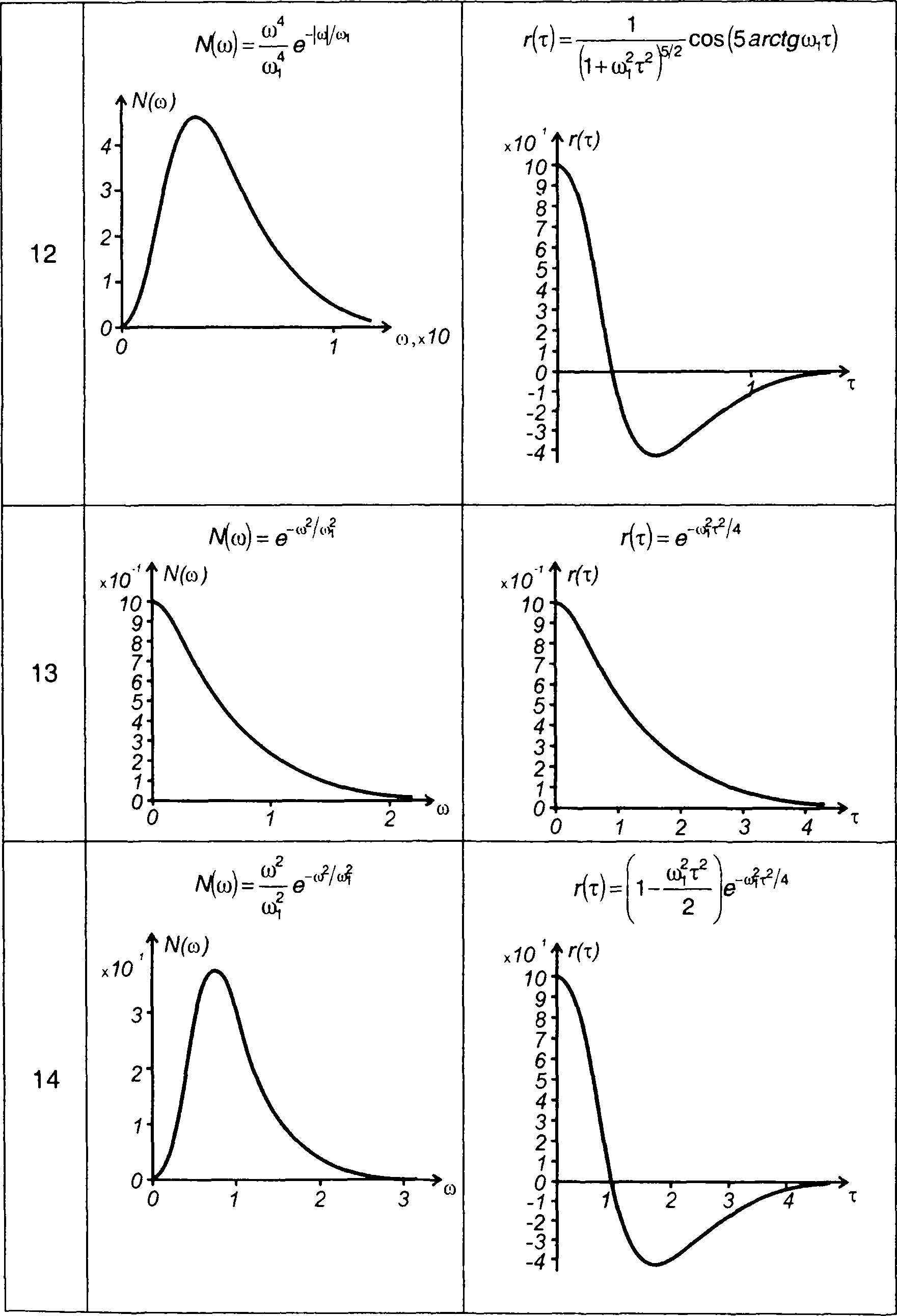
Продолжение таблицы 18.1

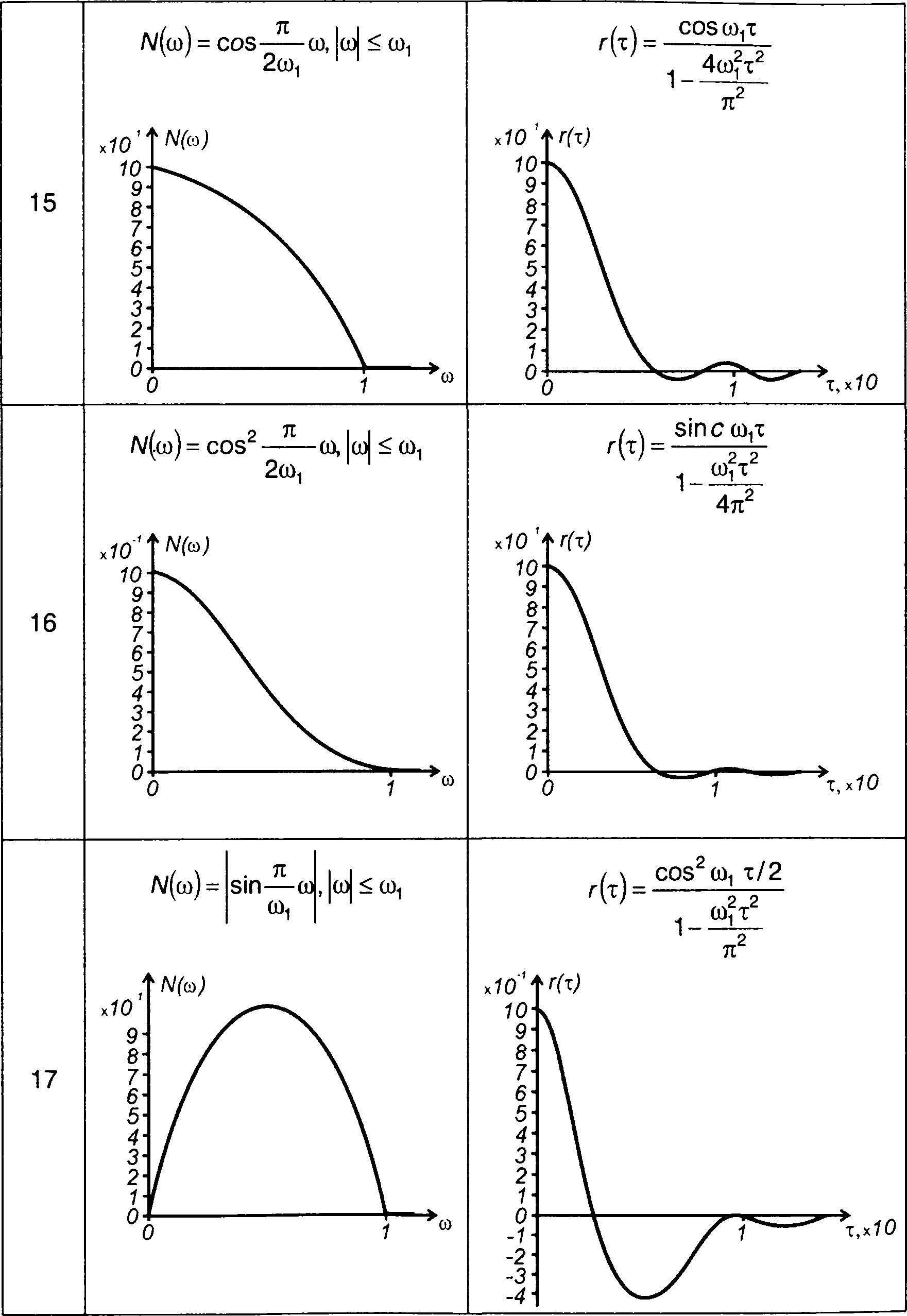
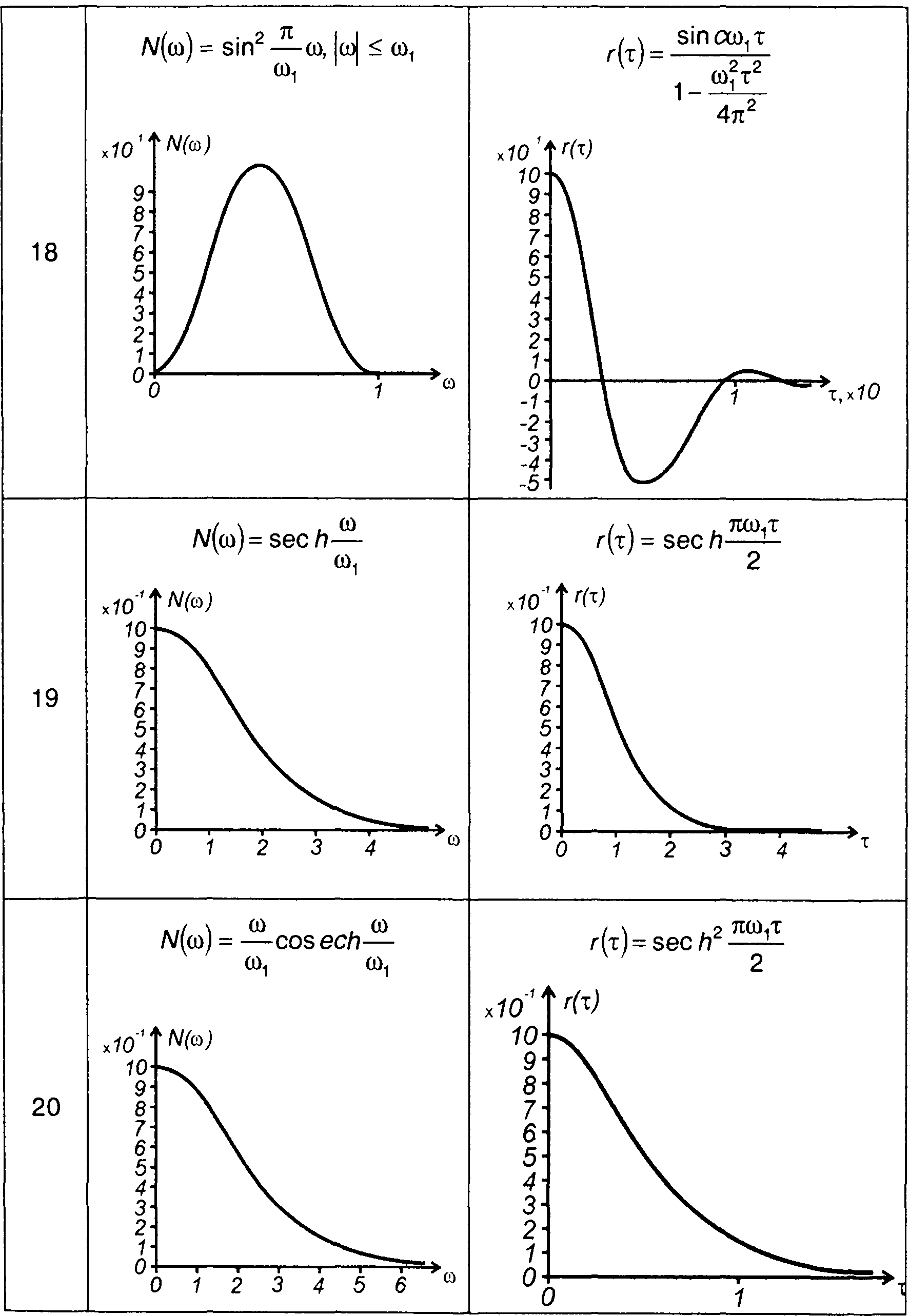
Окончание таблицы 18.1

Исходя из (18.19) получим выражения для преобразований Фу­рье некоторых неинтегрируемых функций.

1. Постоянная составляющая а (разд. 3).

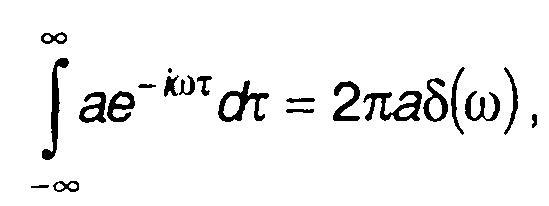(18.20)

2. Гармоническая составляющая cosω₀т (разд. 3).

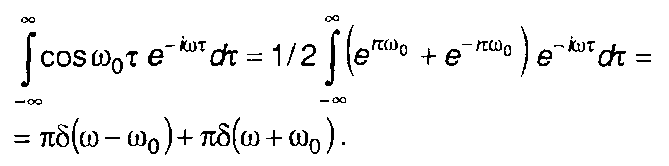(18.21)

3. Произведение R(т) и cosω₀τ.

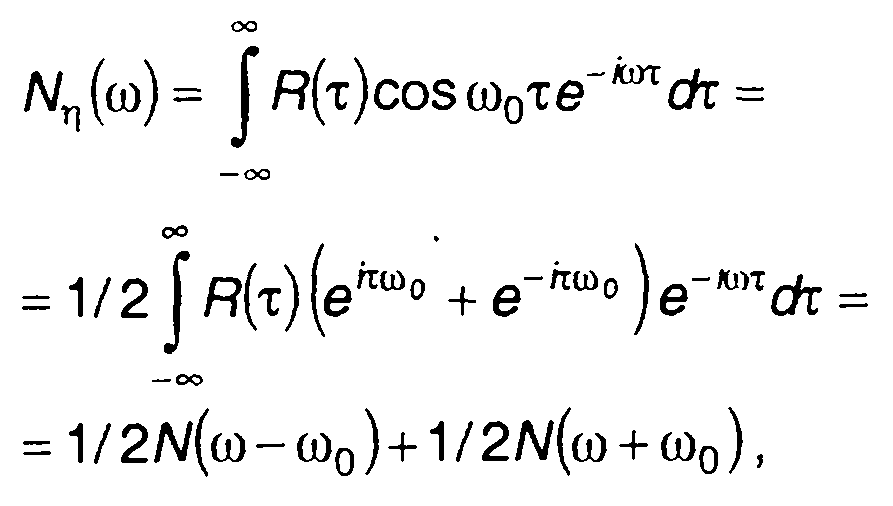(18.22)

где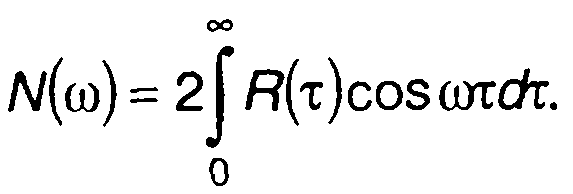

4. Одним из видов случайных процессов, с которыми приходит­ся иметь дело в практике исследований, является стационарный случайный процесс, представляющий сумму квазидетерминированных случайных процессов

(18.23)

где ξ_к- случайная величина; ω_к - постоянная величина.

Каждая составляющая ξ_к cos(ω_kt) представляет гармоническое колебание со случайной амплитудой, распределение вероятностей которой не зависит от времени

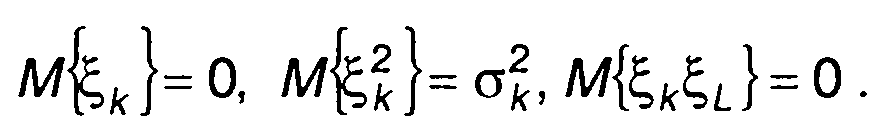(18.24)

Из (18.23) с учетом (18.24) получим корреляционную функцию случайного процесса η(t) в виде

(18.25)

Спектральная плотность мощности случайного процесса опре­деляется преобразованием Фурье R_η(т)

(18.26)

представляет совокупность импульсных функций на частотах ±ω_k.

Рассмотренный случайный процесс называется случайным про­цессом с дискретным спектром.

Приведенные соотношения, иллюстрирующие возможности расширения области преобразования Фурье, использованы в дальнейшем.

18.3.Эффективная ширина спектра случайного процесса

Если для определения ширины корреляционной функции ис­пользуется понятие интервала корреляции, то для спектра случай­ного процесса - эффективной ширины спектра. Эффективная ши­рина спектра определяется как наибольший интервал на оси час­тот, на котором спектральная плотность мощности еще имеет су­щественное для решаемой задачи значение. По аналогии с интер­валом корреляции эффективную ширину спектра случайного про­цесса можно определить на основе различных подходов.

1. Эффективная ширина спектра А определяется заданным зна­чением нормированной спектральной плотности мощности случай­ного процесса (рис. 18.б)

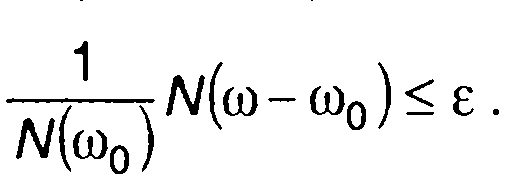(18.27)

Значение частоты ω₀ принимают равной средней частоте спек­тра, при низкочастотном спектре - равной нулю.

2. Эффективная ширина спектра определяется заданным зна­чением интеграла от нормированной спектральной плотности мощности (рис. 18.7).

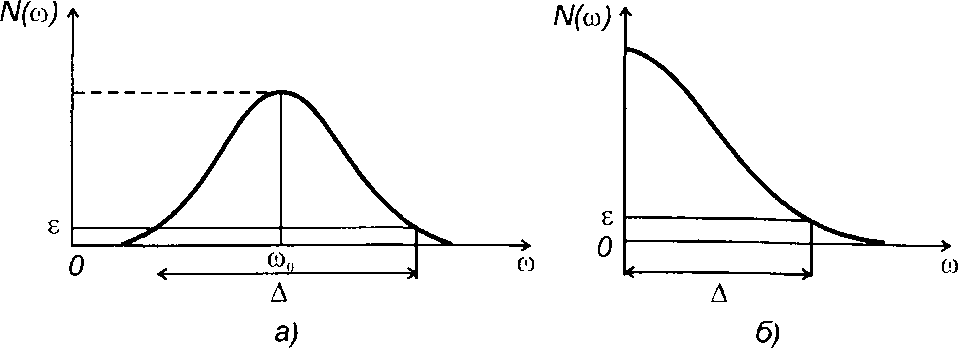
Рис. 18.6

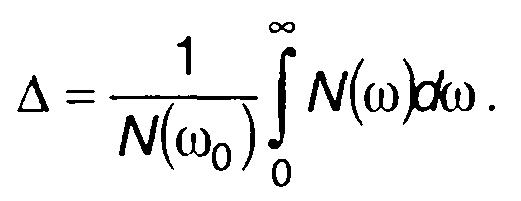(18.28)

Величина 2 ∆ представляет ширину равномерного спектра мощности случайного процесса, имеющего мощность, равную мощности рассматриваемого случайного процесса.

Аналогично соотношениям Хинчина - Винера, записанным для одного случайного процесса - (18.12) и (18.13), можно записать соотношения, связывающие взаимную корреляционную функцию и взаимную плотность мощности двух случайных процессов ξ₁(t) и ξ₂(t)

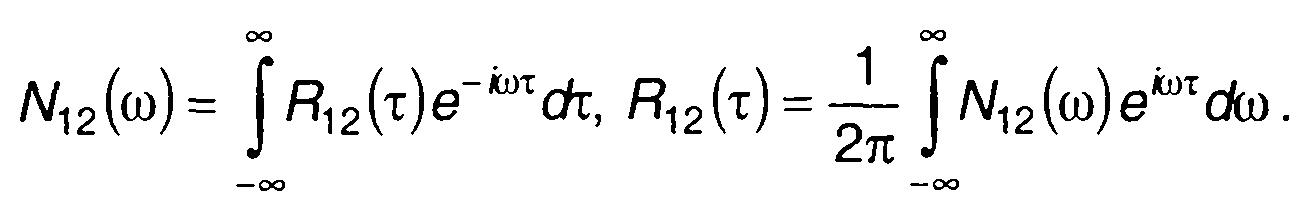(18.29)

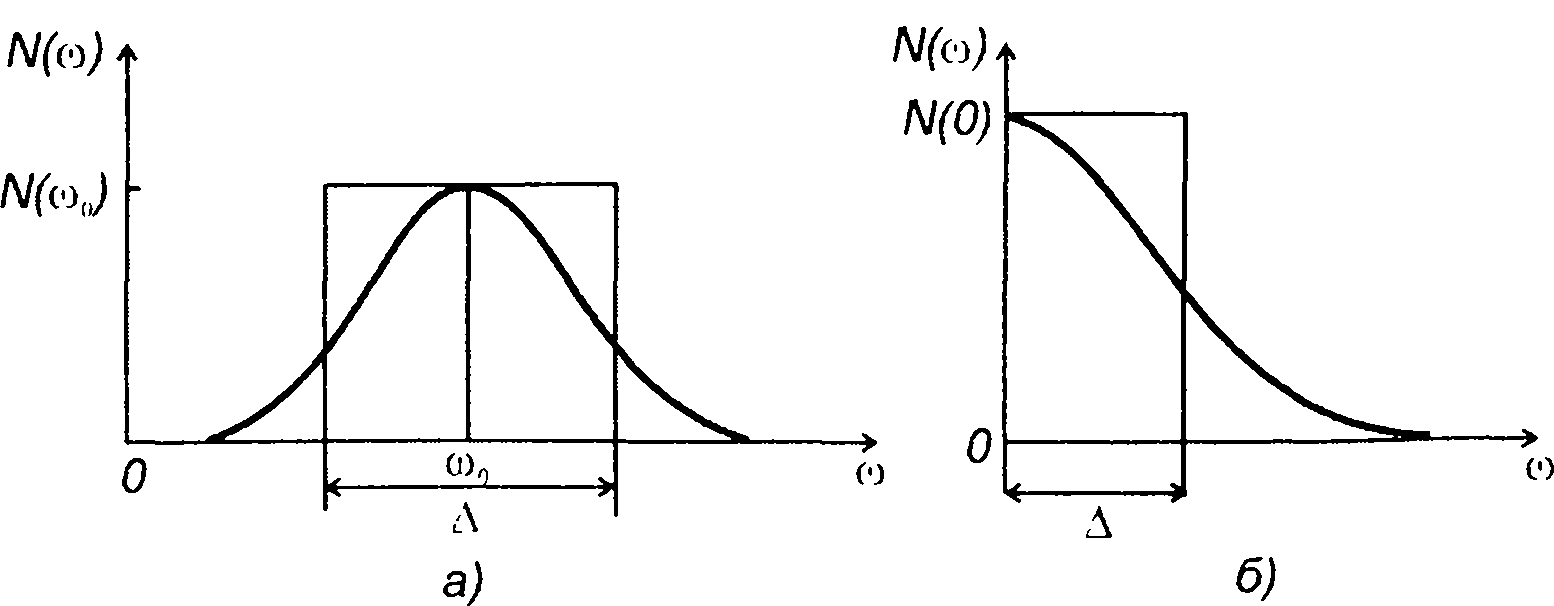
Рис. 18.7

18.4. Спектр производной и интеграла от случайного процесса

Используя свойства преобразования Фурье, установим соотно­шения между спектральной плотностью мощности и корреляцион­ной функцией производной и интеграла от стационарного случай­ного процесса.

Корреляционная функция производной стационарного случай­ного процесса равна второй производной от корреляционной функ­ции, взятой со знаком минус (разд. 17)

Из (18.14) получим

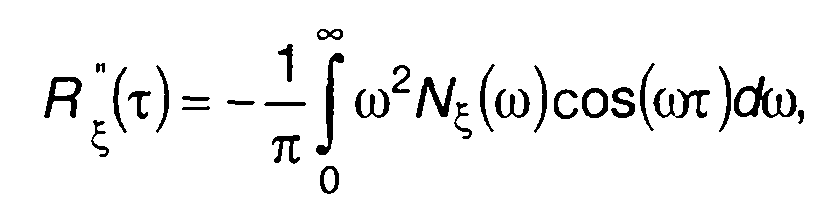(18.30)

где N_ξ(ω) - спектральная мощность случайного процесса ξ(t) .

С учетом (18.30) можем записать соотношение, связывающее спектральные плотности мощности случайного процесса и его про­изводной

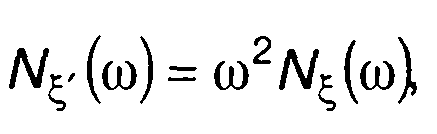(18.31)

где N_ξ`(ω)- спектральная плотность мощности производной слу­чайного процесса.

Средняя мощность производной случайного процесса равна

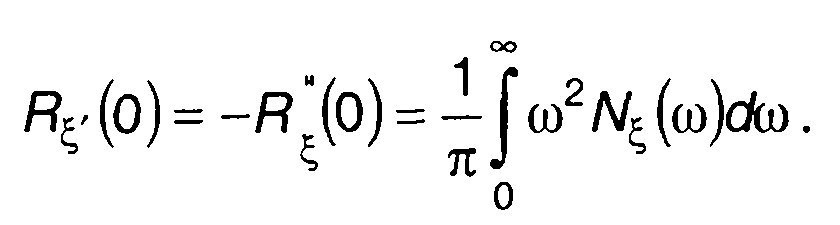(18.32)

Нормированная корреляционная функция производной случай­ного процесса определяется выражением

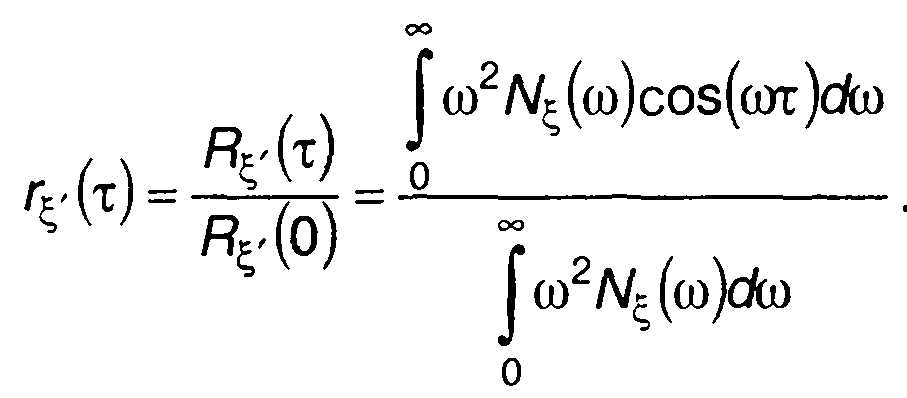(18.33)

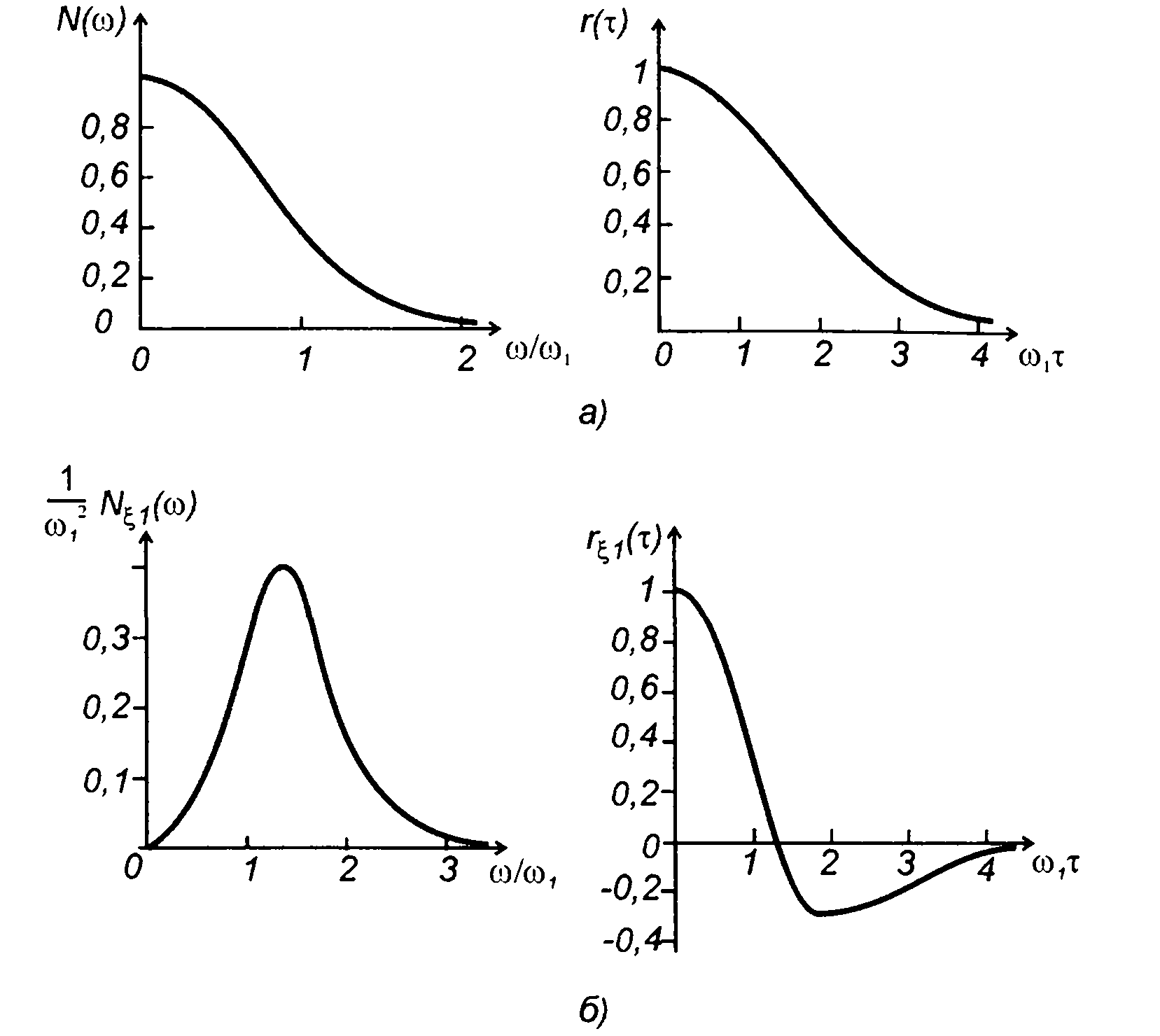
Рис. 18.8

Аналогично для n-й производной случайного процесса ξ(t) за­пишем

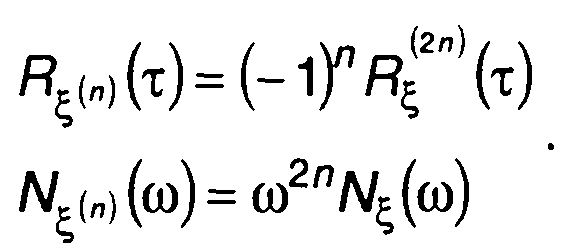(18.34)

В качестве примеров рассмотрим некоторые виды спектров слу­чайных процессов и характеристики их производных.

1. Спектральная плотность мощности и корреляционная функ­ция случайного процесса (рис. 18.8,б)

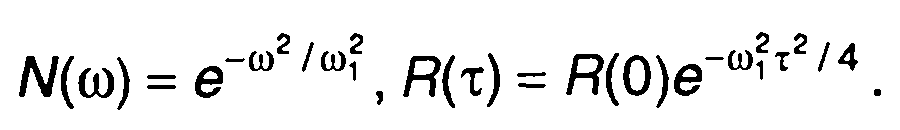
Спектральная плотность мощности и корреляционная функция производной случайного процесса (рис. 18.8,б)

Рис. 18.9

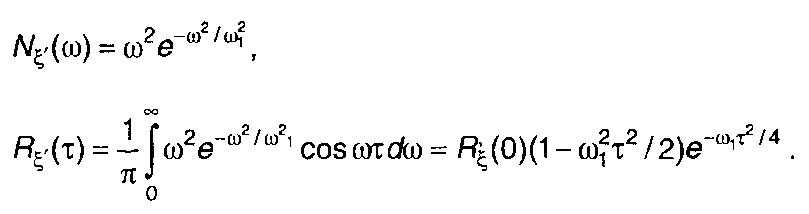
2. Спектральная плотность мощности и корреляционная функ­ция случайного процесса (рис. 18.9,а)

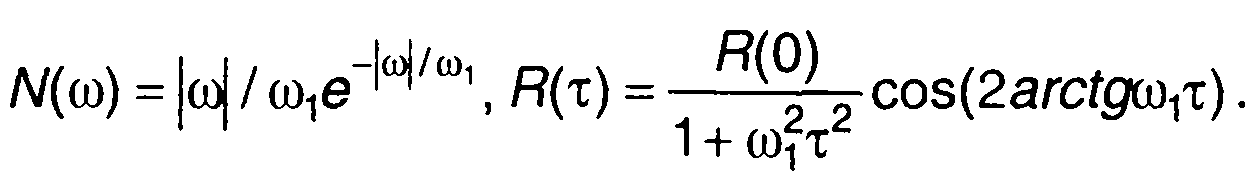
Спектральная плотность мощности и корреляционная функция производной случайного процесса (рис. 18.9,б)

Рис. 18.10

Используя полученные соотношения, можно получить и выра­жение для спектральной плотности мощности интеграла от слу­чайного процесса r|(t)

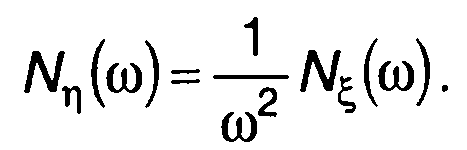(18.35)

Так, если спектральная плотность мощности и корреляционная функция случайного процесса описывается выражениями (рис. 18.10,а)

то спектральная плотность мощности и корреляционная функция интеграла от случайного процесса равны (рис. 18.10,б)

Анализ графиков рис. 18.8-18.10 позволяет оценить влияние дифференцирования и интегрирования на характеристики случай­ного процесса.

18.5. Дискретизация случайного процесса и его характеристик

Исходные данные о случайном процессе получаются в резуль­тате измерений его характеристик, в первую очередь, корреляци­онной функции и спектральной плотности мощности. Указанные характеристики используются для определения других, необходи­мых при анализе случайного процесса. Как правило, эти характе­ристики определяются как дискретные функции времени (задерж­ки) и частоты. Дискретные характеристики случайного процесса получаются и при цифровой обработке колебаний. В связи с этим возникнет ряд важных для практики задач:

выбор интервала дискретизации характеристик случайного про­цесса;

установление соотношений между дискретными характеристи­ками случайных процессов;

восстановление непрерывных характеристик случайных процес­сов по дискретным и др.

В дальнейшем рассматриваются первые две из названных за­дач, переход от дискретных к непрерывным характеристикам (ин­терполяция характеристик случайных процессов) описан в первой части.

18.5.1. Выбор интервала дискретизации случайного процесса

Преобразование Фурье, используемое при анализе детермини­рованных сигналов, связывает временную функцию, описывающую сигнал, и спектральную плотность сигнала. При анализе случайных процессов преобразование Фурье устанавливает связь между кор­реляционной функцией и спектральной плотностью мощности слу­чайного процесса. Эта аналогия позволяет перенести некоторые выводы в отношении детерминированных сигналов на характери­стики случайных процессов.

Возможность представления непрерывной корреляционной функции случайного процесса ее дискретными значениями опре­деляется так же, как и детерминированных сигналов. Корреляци­онная функция полностью определяется дискретными отсчетами,

выполняемыми через интервал времени, выбираемый из условия: τ1<π/ω_m, где ω_m - максимальная частота в спектре случайного процесса.

Восстановление непрерывной корреляционной функции по дис­кретным значениям возможно, например, с помощью ряда Котель­никова (рис. 18.11)

(18.36)

Дискретная корреляционная функция получается при обработке выборочных значений случайного процесса. Для центрированного случайного процесса

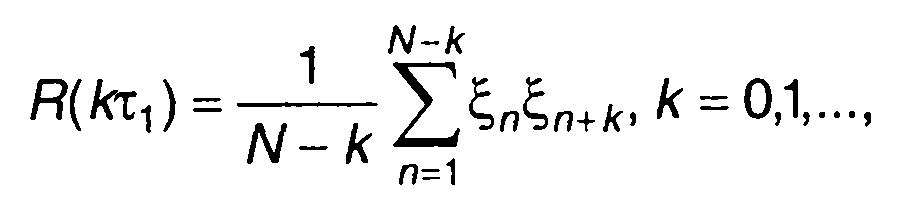(18.37)

где ξ_n,ξ_n+k - выборочные значения случайного процесса ξ(nτ₁) и ξ[(n+ k)τ₁ ]; τ- интервал дискретизации; kх₁ - смешение во вре­мени; N - общее число выборочных значений.

Ограничение, накладываемое на выбор интервала дискретиза­ции корреляционной функции, определяет интервал дискретизации и самого случайного процесса.

Аналогичный вывод можно сделать относительно интервала дис­кретизации по частоте при описании спектральной плотности мощно­сти случайного процесса ее дискретными значениями (рис. 18.12).

Рис. 18.11

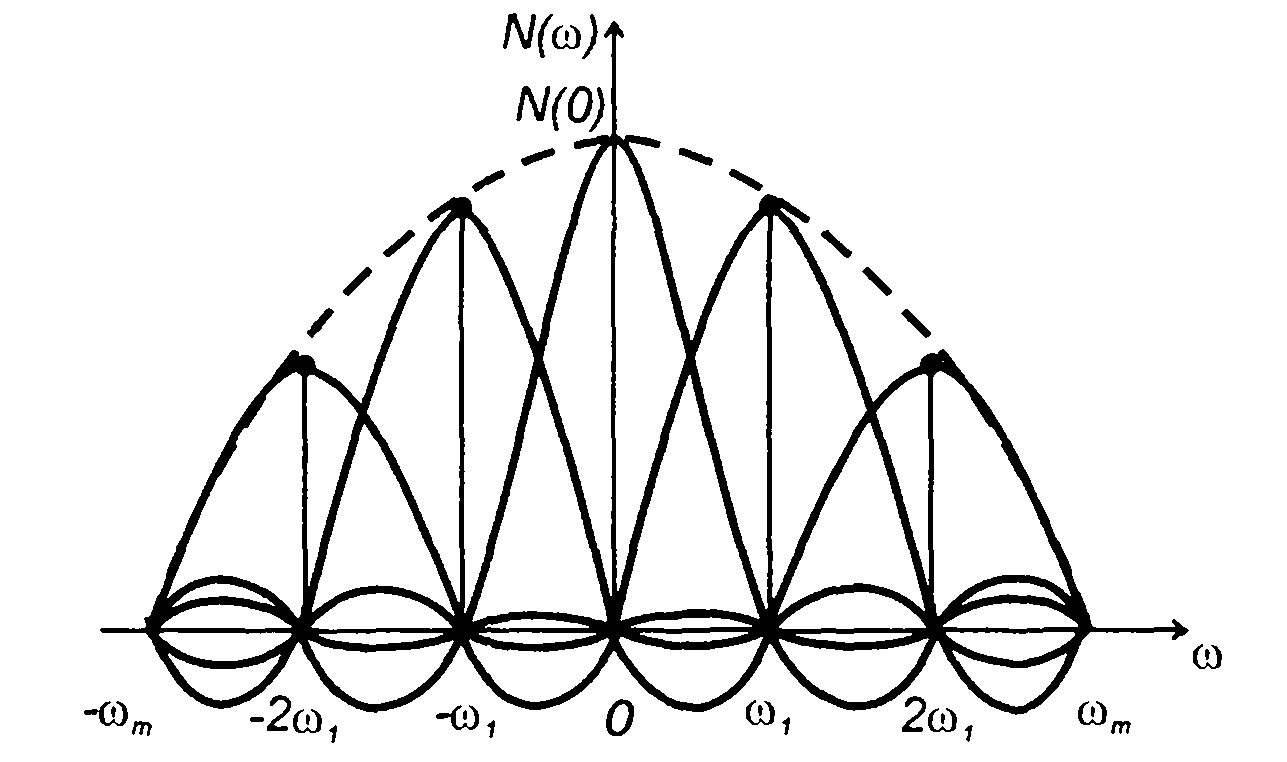
Рис. 18.12

Интервал дискретизации по частоте выбирается из условия ω₁ < π/τ_k, где τ_к- минимальное значение задержки, при котором

корреляционная функция может быть принята равной нулю. Ряд Котельникова, определяющий спектральную плотность мощности случайного процесса через ее дискретные значения, имеет вид

(18.38)

В качестве предельных значений ω_m и τ_k могут быть выбраны;

эффективная ширина спектра и интервал корреляции. Более стро­гий подход к их определению лишен смысла, интервалы дискрети­зации - по времени и частоте устанавливаются неравенствами. Общее число выборочных значений равно

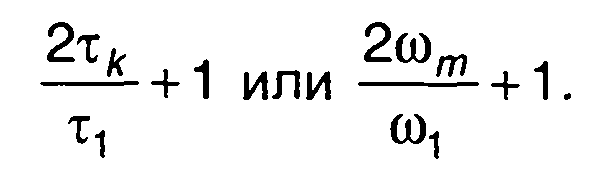
Используя дискретные значения корреляционной функции, про­ведем ее ступенчатую аппроксимацию. Выражение для спектраль­ной плотности случайного процесса запишем в виде

(18.39)

Выражение (18.39) позволяет получить непрерывную функцию N(ω) с использованием дискретных значений корреляционной функции.

Аналогично запишем выражение для корреляционной функции случайного процесса

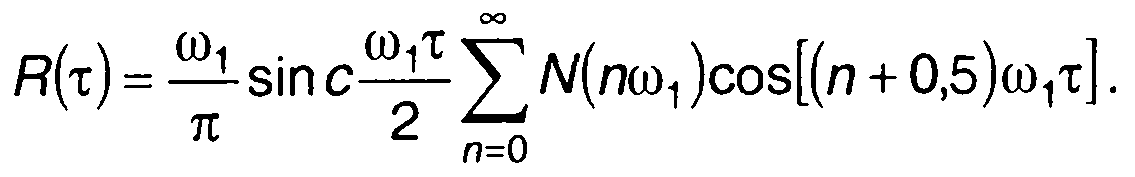(18.40)

Выражения (18.39), (18.40) могут быть применены для получения алгоритмов расчета спектральной плотности мощности по дискрет­ным значениям корреляционной функции и корреляционной функ­ции - по дискретным значениям спектральной плотности мощности.

18.5.2. Дискретное преобразование Фурье (ДПФ)

Как и при расчете характеристик детерминированных сигналов, можно записать ДПФ, связывающее дискретную корреляционную функцию с дискретной спектральной плотностью случайного процесса.

Соотношения, связывающие корреляционную функцию и спек­тральную плотность мощности случайного процесса

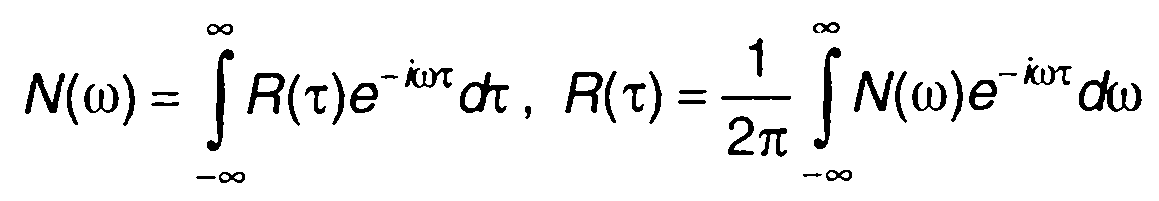
при достаточно малых значениях τ₁ и ω₁, могут быть преобразованы к виду

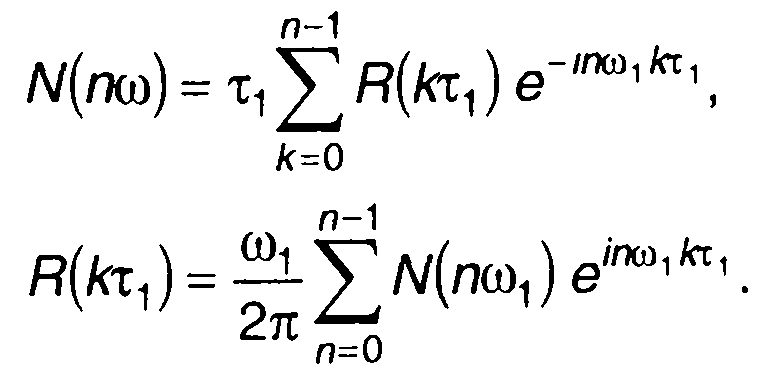(18.41)

Выражения (18.41) представляют дискретное преобразование Фурье (прямое и обратное), связывают дискретные характеристики случайного процесса: корреляционную функцию и спектральную плотность мощности. Они позволяют получить удобные алгоритмы расчета указанных характеристик.

При расчете по (18.41) можно перейти к алгоритмам, значитель­но сокращающим объем вычислительных операций - алгоритмам быстрого преобразования Фурье (БПФ).

Раздел 19.

УЗКОПОЛОСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ

Узкополосные случайные процессы составляют широкий класс случайных процессов. К ним в первую очередь относится колеба­ние, модулированное сигналом. В качестве несущего колебания может быть гармоническое или узкополосное случайное колеба­ние, в качестве модулирующего - детерминированный сигнал или случайный сигнал. Особенности узкополосных процессов, как и узкополосных детерминированных сигналов, делают целесообраз­ным их отдельное рассмотрение.

В разделе дается описание и методы анализа узкополосных случайных процессов. Рассматривается наиболее распространен­ный вид узкополосного случайного процесса - гармоническое ко­лебание, модулированное случайным процессом.

19.1. Описание и характеристики узкополосных процессов

19.1.1. Описание узкополосного случайного процесса

Как и детерминированный сигнал, случайный процесс называ­ется узкополосным, если его спектр сосредоточится в узкой полосе частот около средней частоты (рис. 19.1).

Узкополосный случайный процесс описывается выражением

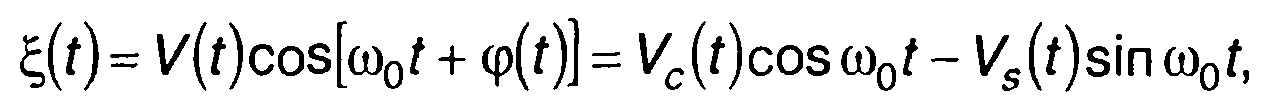(19.1)

где ω₀ - несущая частота; V(t),φ(t)- огибающая и фаза случайного процесса;

(19.2)

Представление случайного процесса в виде (19.1) не ограниче­но классом узкополосных процессов, однако для узкополосных процессов оно оказалось наиболее удобным, V(t) и φ(t) имеют на­глядное физическое содержание. Реализация узкополосного слу­чайного процесса представляет гармоническое колебание с мед­ленно меняющейся амплитудой и частотой (фазой) (рис. 19.2).

Рис. 19.1

В отличие от детерминированного сигнала V(t) и φ(t) случайного процесса являются случайными функциями.

Выражение для узкополосного случайного процесса часто удоб­нее записывать в комплексной форме

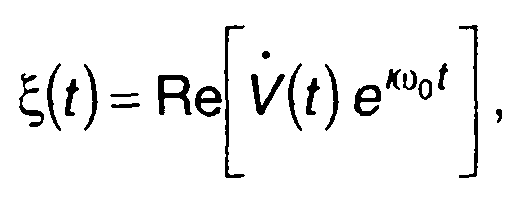(19.3)

где V(t) - комплексная огибающая случайного процесса:

(19.4)

Из (19.4) с учетом (19.2) получим

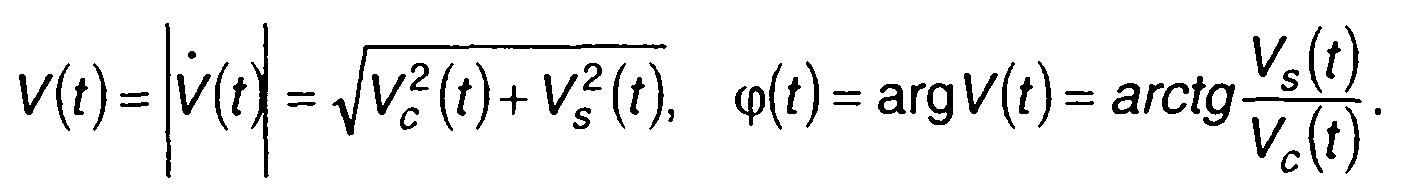(19.5)

Корреляционная функция узкополосного случайного процесса ξ(t) определяется как

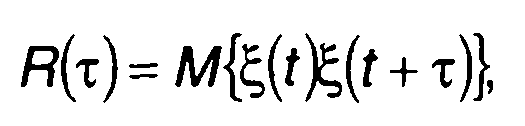(19.6)

где М {...} - символ усреднения.

Рис. 19.2

Учитывая следующее соотношение для действительной части комплексной величины z

(19.7)

где z* - комплексно сопряженная величина, из (19.6) с учетом (19.3) получим

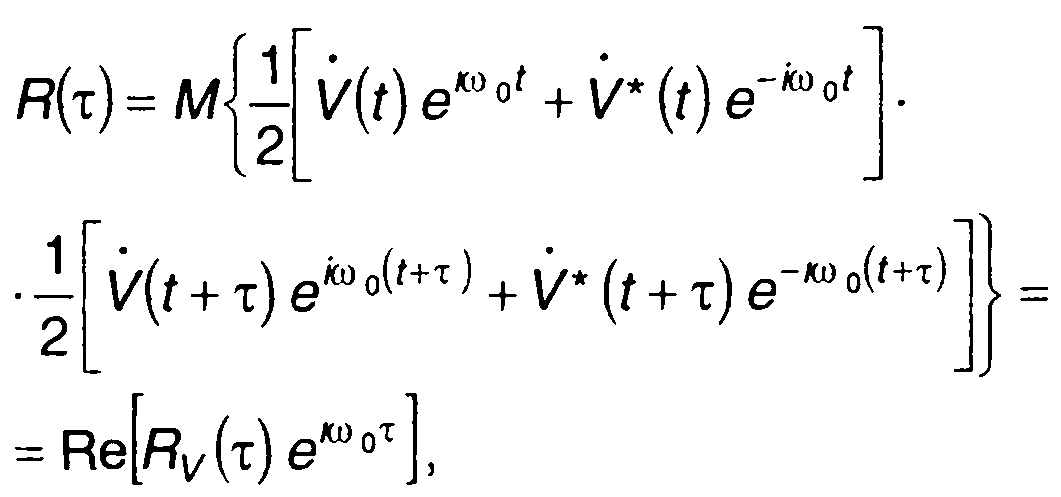(19.8)

гдеR_v(т) - корреляционная функция комплексной огибающей узко­полосного случайного процесса:

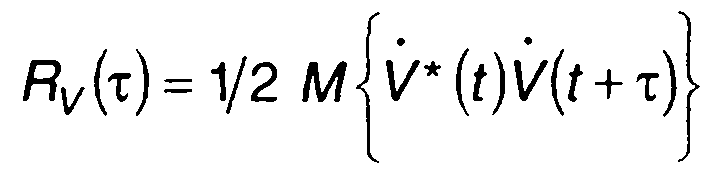(19.9)

Как следует из (19.8), при заданном значении несущей частоты корреляционная функция комплексной огибающей полностью оп­ределяет корреляционную функцию узкополосного случайного процесса. Это позволяет при нахождении корреляционной функции узкополосного случайного процесса ограничиться определением R_v( т).

В качестве примеров приведем несколько видов функций Rv(т).

1. Корреляционной функции комплексной огибающей (рис. 19.3,а)

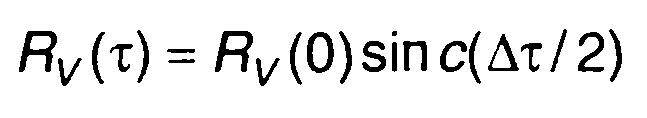
соответствует корреляционная функция узкополосного случайного процесса (рис. 19.3,б)

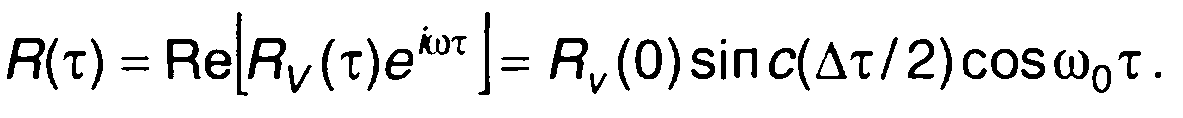
2. Корреляционной функции комплексной огибающей (рис. 19.4а)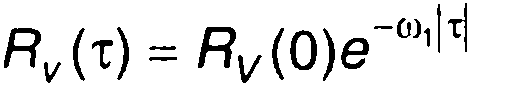

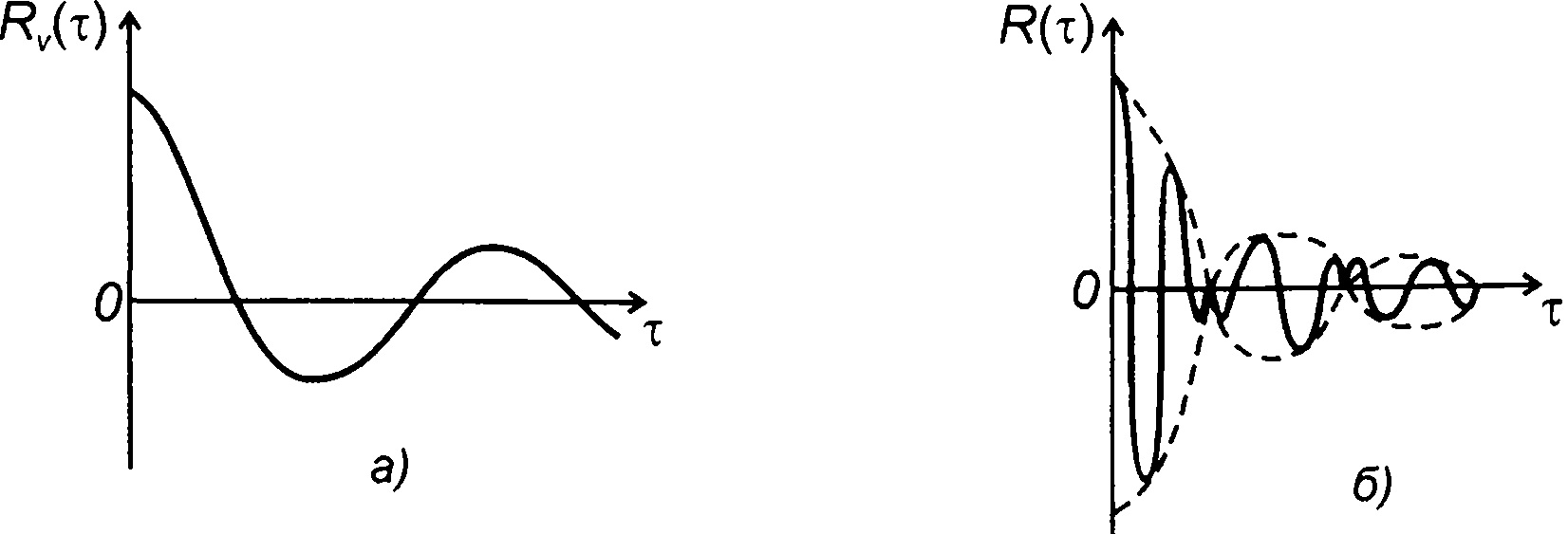
Рис. 19.3

соответствует корреляционная функция узкополосного случайного процесса (рис. 19.4, б)

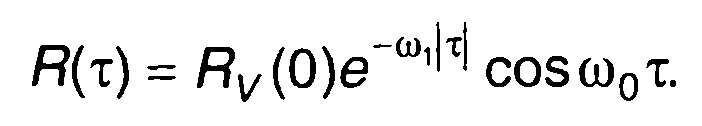
3. Корреляционной функции комплексной огибающей (рис. 19.5,а)

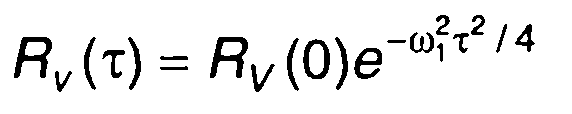
соответствует корреляционная функция узкополосного случайного процесса (рис. 19.5 б)

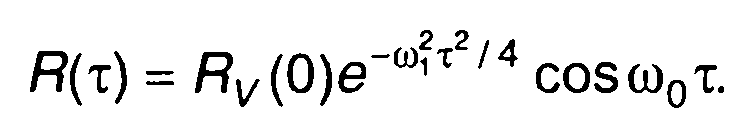
Спектральная плотность мощности случайного процесса опре­деляется как преобразование Фурье корреляционной функции. Выражение для корреляционной функции узкополосного случайно­го процесса (19.8) с учетом (19.7) запишем в виде

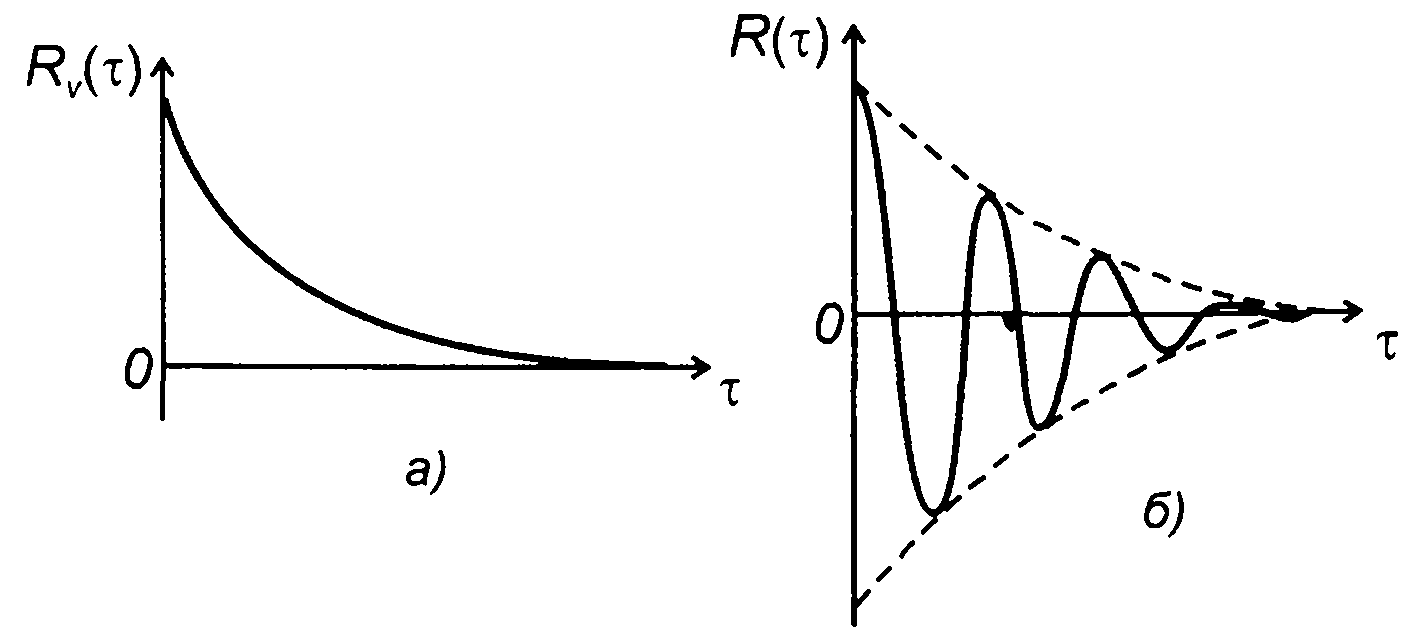
Рис.19.4

Рис. 19.5

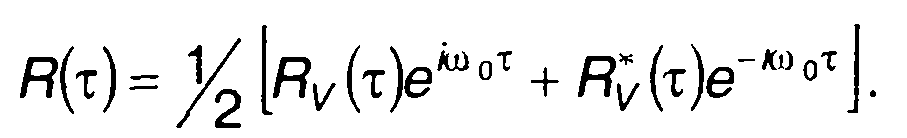(19.10)

Преобразование Фурье левой и правой частей (19.10) дает

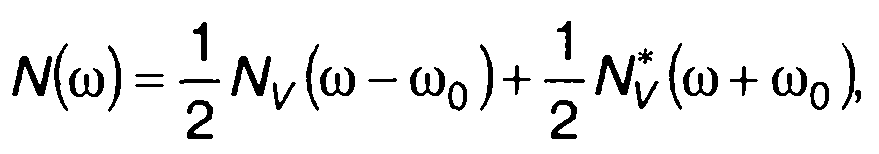(19.11)

где N_v (ω) - спектральная плотность мощности комплексной оги­бающей

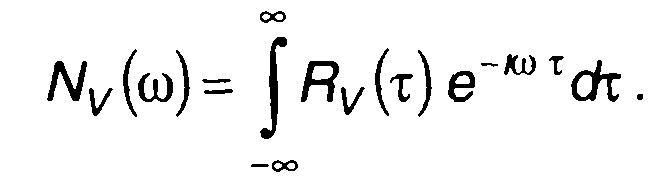(19.12)

Как следует из (19.11), спектр узкополосного процесса состоит из двух зеркально-симметричных по форме составляющих, распо­ложенных в области частот ±ω₀ (рис.19.6). Спектр случайного про­цесса в области положительных значений частоты описывается первым слагаемым в (19.11), в области отрицательных значений - вторым слагаемым. При заданном значении несущей частоты ω₀ спектр случайного процесса полностью определяется спек­тральной плотностью мощности комплексной огибающей. Переход от спектра комплексной огибающей к спектру случайного процесса предполагает перенос низкочастотного спектра, описываемого N_v(ω), в область частот ±ω₀ (с коэффициентом 1/2). Таким обра­зом, при спектральном анализе узкополосного случайного процес­са достаточно исследовать только спектральную плотность мощ­ности его комплексной огибающей.

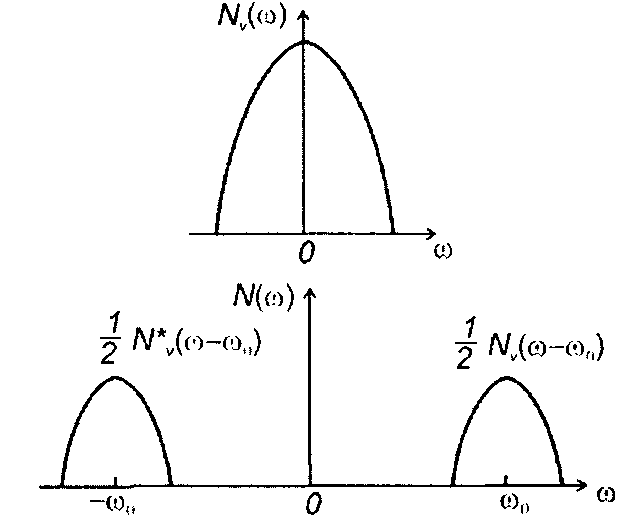
Рис. 19.6

Рассмотрим несколько видов спектров комплексной огибающей случайного процесса.

1. Спектральной плотности мощности комплексной огибающей (рис. 19.7,а)

соответствует спектральная плотность мощности случайного про­цесса (рис. 19.7,6) при ω > 0

2. Спектральной плотности мощности комплексной огибающей (рис. 19.8, а)

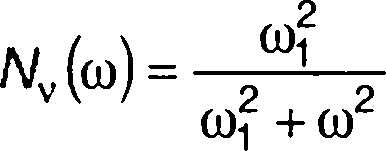
Рис. 19.7

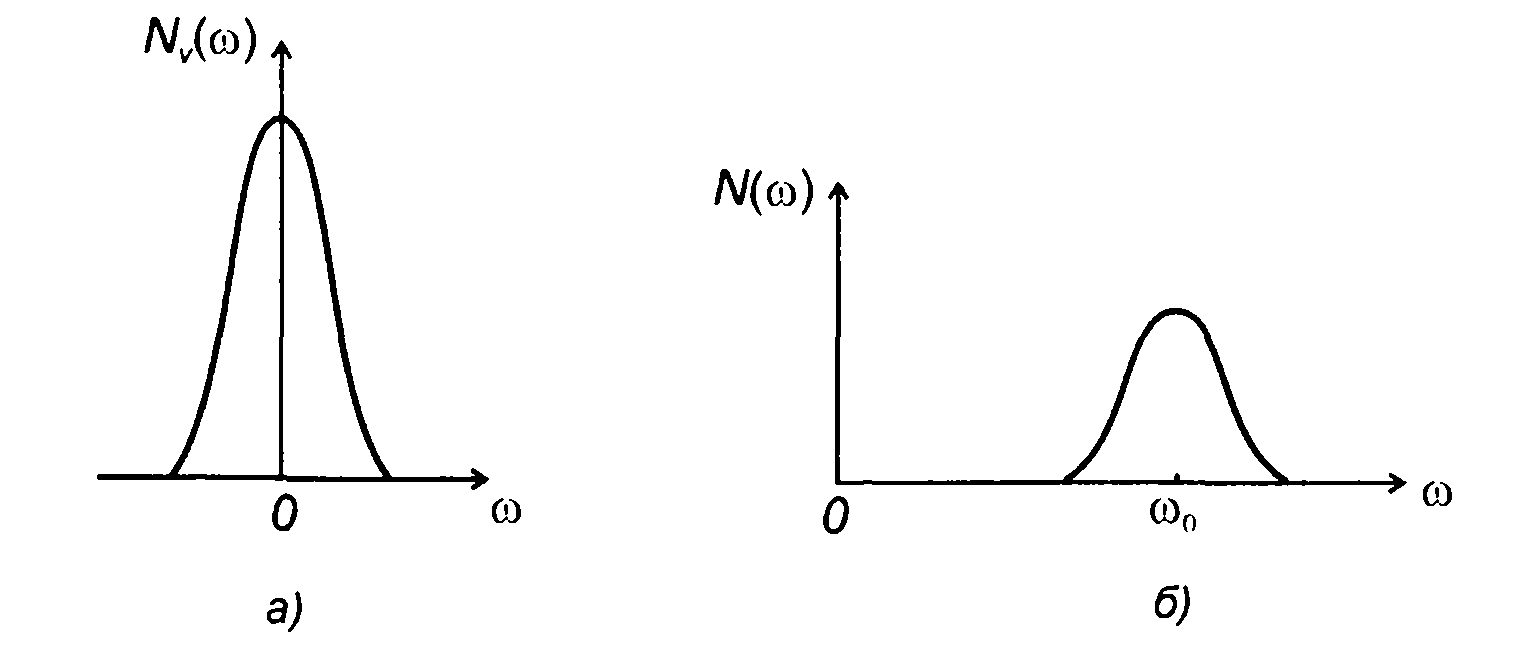
Рис.19.8

соответствует спектральная плотность мощности случайного про­цесса (рис. 19.8,6) при ω > 0

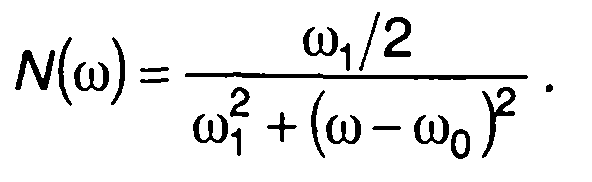
3. Спектральной плотности мощности комплексной огибающей (рис.19.9,а)

соответствует спектральная плотность мощности случайного про­цесса (рис.19.9, б) при ω > 0

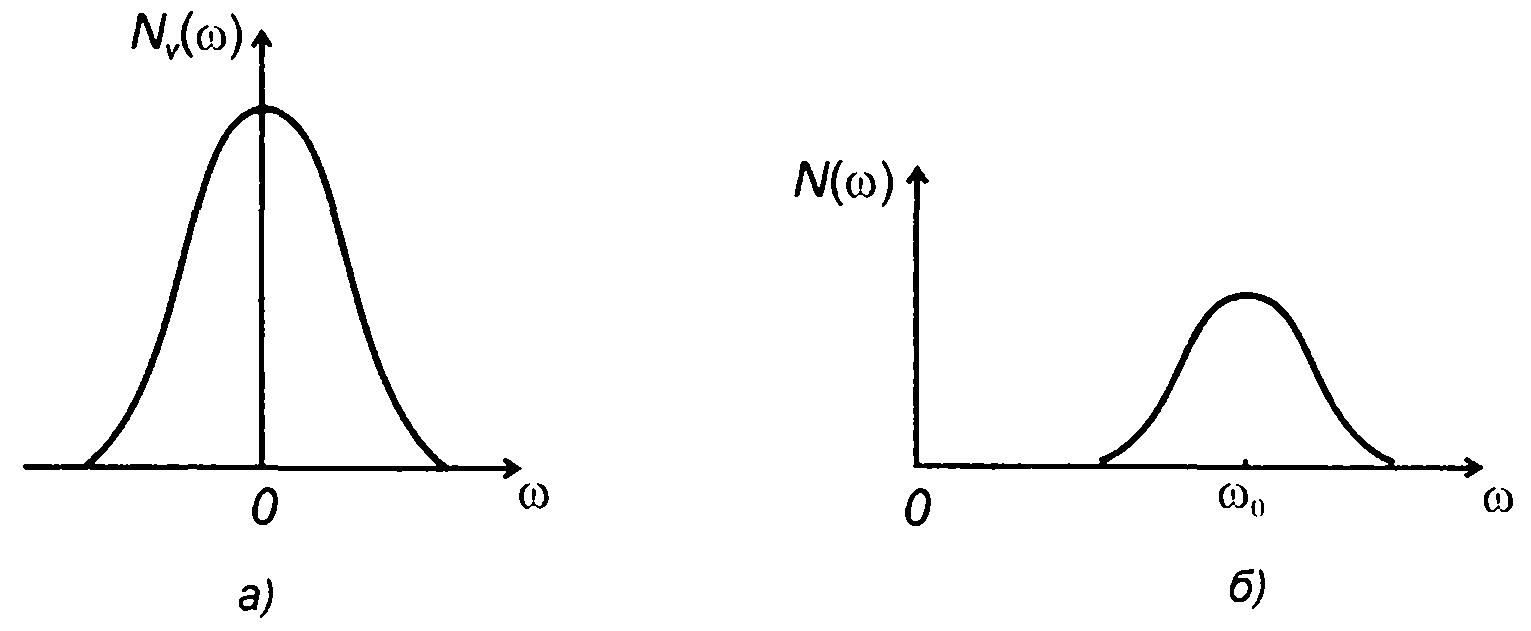
Рис.19.

19.1.2. Белый шум

Идеализацией широкополосного случайного процесса является белый шум - случайный процесс с постоянной спектральной плот­ностью мощности на всех частотах (рис. 19.10,а)

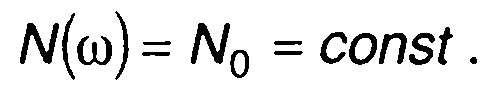(19.13)

Корреляционная функция белого шума

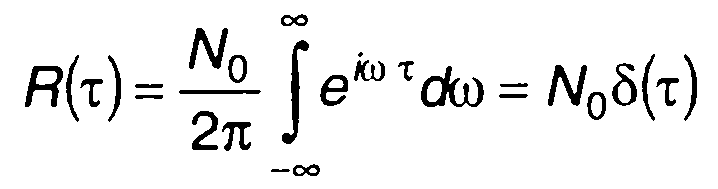(19.14)

представляет импульсную функцию в начале координат (рис. 19.10,6). Нормированная корреляционная функция белого шума равна

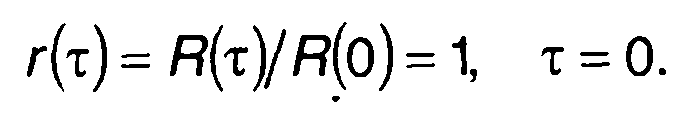(19.15)

Белый шум является только моделью реальных широкополос­ных случайных процессов: мощность реального случайного про­цесса ограничена, мощность белого шума бесконечна. Однако введение понятия белого шума является полезным, в частности, при анализе прохождения случайных процессов через радиотехни­ческие цепи, и может не оказывать существенного влияния на ре­зультаты, полученные при его использовании как модели реально­го процесса.

19.2. Распределение вероятностей огибающей и фазы узкополосного гауссовского процесса

Обратимся к записи узкополосного случайного процесса ξ(t) в виде

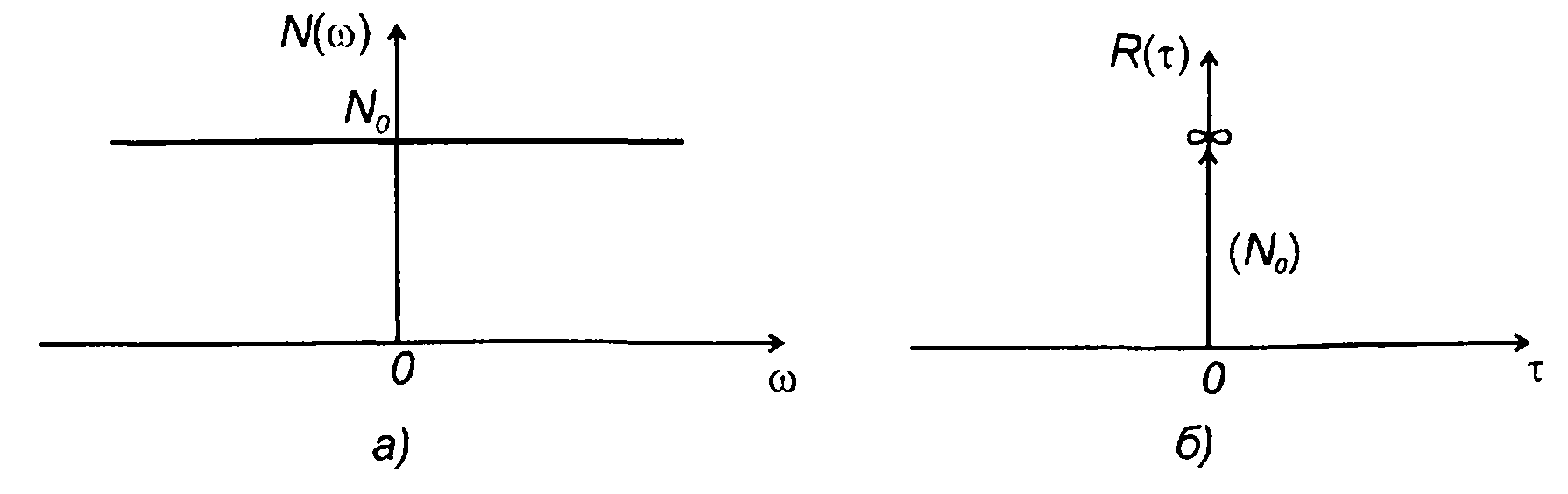
Рис. 19.10

(19.16)

где

(19.17)