ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 19 страница

Для стационарного случайного процесса имеем

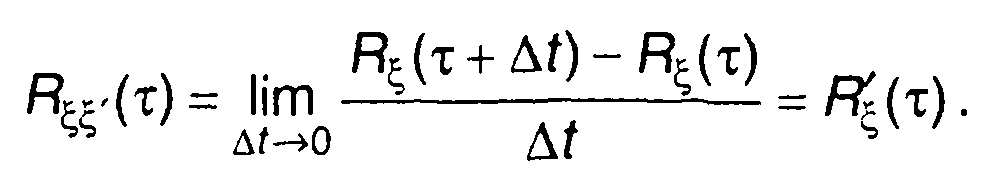(17.78)

Изменив порядок следования случайного процесса и его производной в (17.73), установим

(17.79)

Из выражения для определения взаимной корреляционной функции получим

(17.80)

Таким образом, взаимная корреляционная функция случайного процесса и его производной для одного и того же момента времени равна нулю.

Линейное преобразование не изменяет нормального закона распределения. Следовательно, если существует производная от гауссовского процесса, то она имеет нормальное распределение - представляет также гауссовский процесс. Его одномерная ПРВ описывается выражением

(17.81)

где σ_n² - дисперсия производной гауссовского процесса, σ_n² = -R"ξ(0).

Используя корреляционную функцию гауссовского процесса, можно записать выражение и для n-мерной ПРВ производной любого порядка.

Гауссовский процесс и его производная, рассматриваемые в один и тот же момент времени, как это следует из (17.80), имеют взаимную корреляционную функцию, равную нулю, являются независимыми. Выражение для их совместной ПРВ запишется в виде

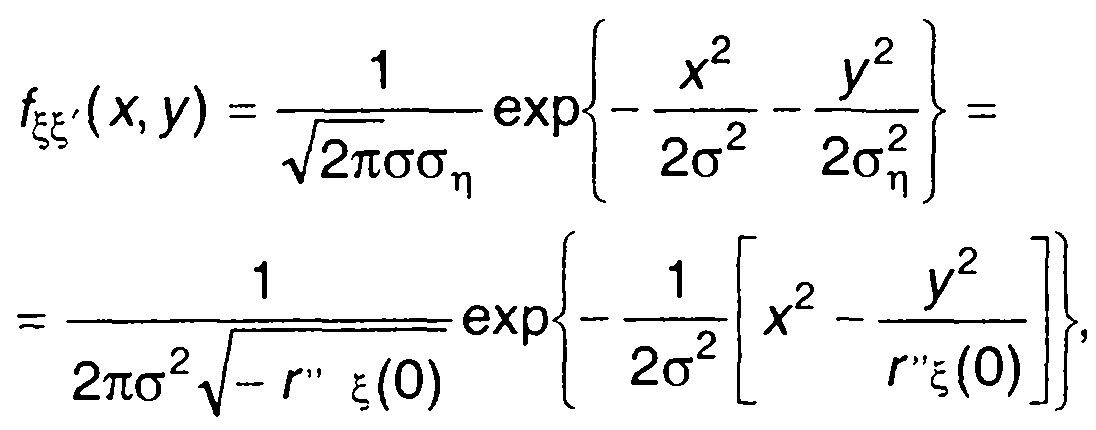(17.82)

где

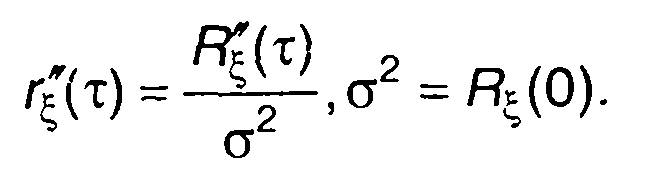(17.83)

Аналогично можно записать выражение и для совместной n-мерной ПРВ гауссовского процесса и его производной любого порядка.

17.5. Распределение вероятностей интеграла от случайного процесса

Интеграл от случайного процесса запишем в виде

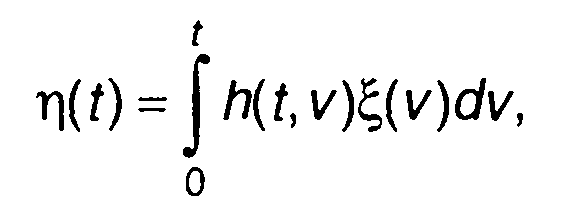(17.84)

где h(t,v) - заданная функция.

Такой интеграл обычно встречается при анализе прохождения случайного процесса через линейную цепь.

Интеграл представляет функцию случайного процесса, к которой сходится интегральная сумма. Таким образом, интегрирование представляет линейное преобразование случайного процесса.

Математическое ожидание случайного процесса, описываемого (17.84), равно

(17.85)

Для стационарного случайного процесса получим

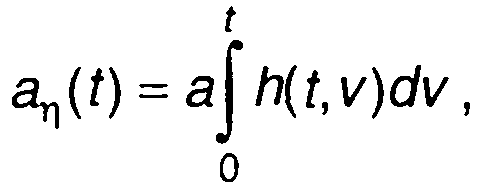(17.86)

где а- математическое ожидание случайного процесса.

Корреляционная функция интеграла от случайного процесса определяется выражением

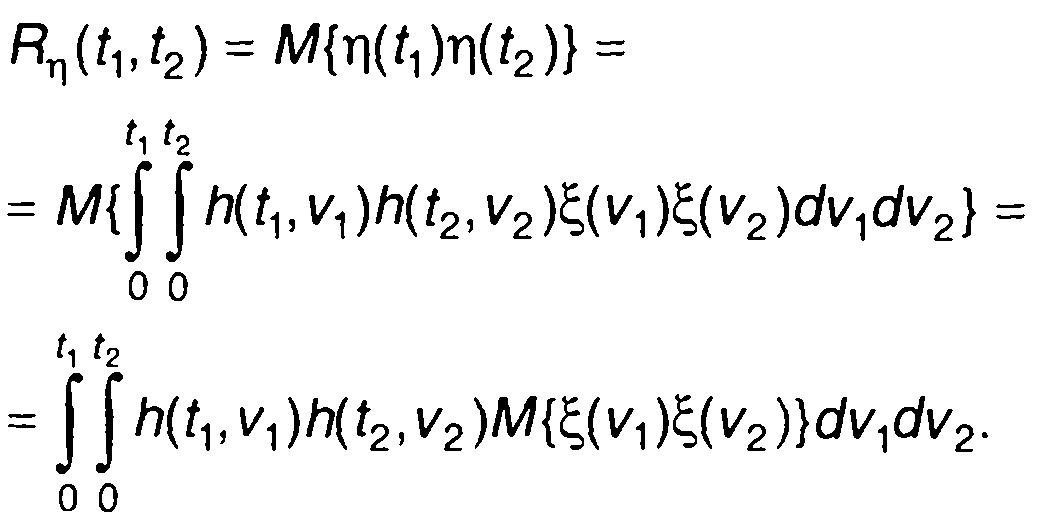(17.87)

Интегрирование как линейная операция не изменяет закона распределения гауссовского процесса. Одномерная ПРВ интеграла от гауссовского процесса ξ(t) имеет вид

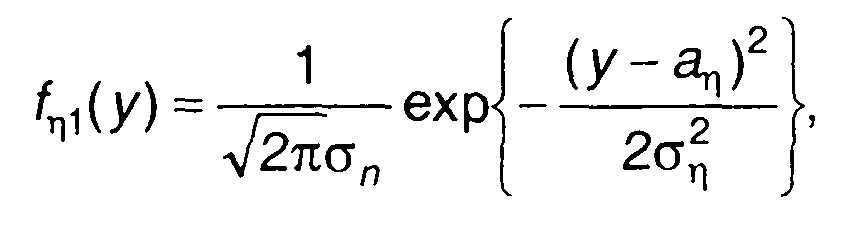(17.88)

где а_η, σ_η² - математическое ожидание и дисперсия интеграла от гауссовского процесса

(17.89)

17.6. Характеристическая функция случайных процессов

Понятие характеристической функции может быть распространено на любую конечную совокупность случайных процессов. Так характеристическая функция случайных процессов ξ₁ и ξ₂, имеющая порядок n+т, определяется выражением

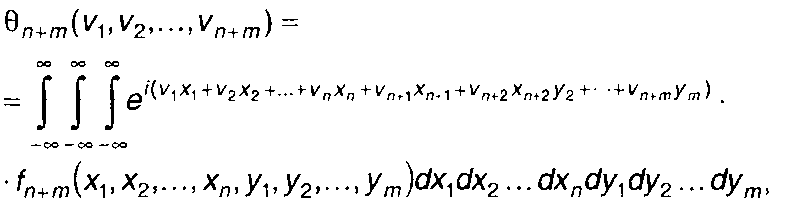(17.90)

где f_n₊_m(...) - n+т-мерная ПРВ случайных процессов ξ₁(t) и ξ₂(t).

Для независимых случайных процессов можем записать

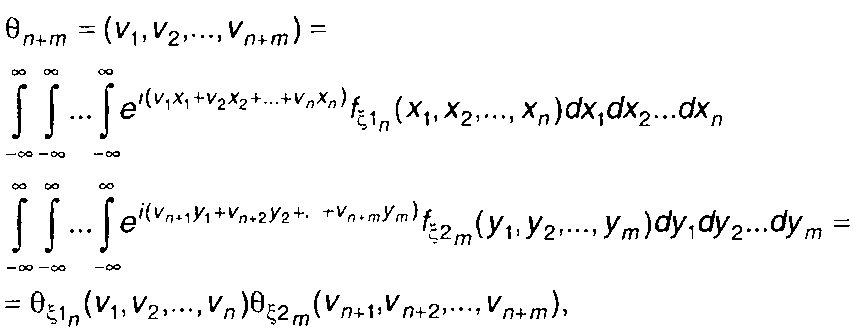(17.91)

где f_ξ₁_n (...) - n-мерная ПРВ случайного процесса ξ₁(t); f_ξ₂_m (...) - т-мерная ПРВ случайного процесса ξ,₂(t).

Таким образом, характеристическая функция независимых случайных процессов равна произведению характеристических функций каждого из них.

Если характеристическая функция случайных величин ξ₁, ξ₂,..., ξ_n

равна θ_n(v₁, v₂,..,v_n), то характеристическая функция случайных величин

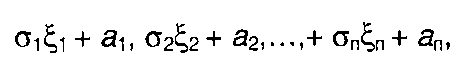
где σ_k, а_k- действительные постоянные, определяется выражением

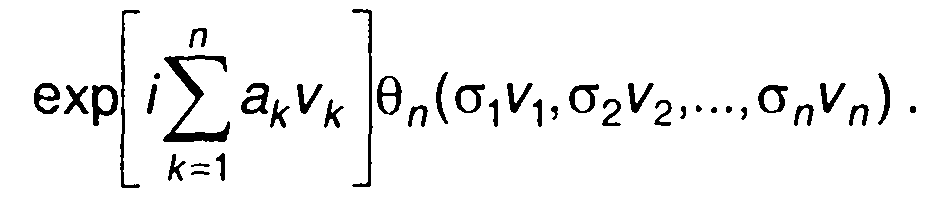(17.92)

Характеристическая функция п случайных величин ξ₁, ξ₂,..., ξ_n,

имеющих нормальное распределение, описывается выражением

(17.93)

где а_к ,о_к - математическое ожидание и дисперсия случайной величины ξ_k; r_к_l - нормированная корреляционная функция случайных величин ξ_k, ξ_l.

Использование характеристических функций при анализе случайных процессов в ряде случаев позволяет упростить операции и сделать анализ более эффективным.

17.7. Метод характеристических функций

Одной из прикладных задач теории случайных процессов является определение характеристик распределения суммы нескольких независимых случайных величин - выборочных значений случайных процессов.

Такая задача решается, например, при оценивании помехоустойчивости системы обнаружения сигнала. Решение ее с получением непосредственно выражения для ПРВ функции случайных величин связано с большими, часто непреодолимыми, трудностями.

Более удобным оказывается подход к определению ПРВ через характеристическую функцию. Характеристическая функция суммы независимых величин определяется как произведение характеристических функций каждой из них. Переход к ПРВ от характеристической функции представляет преобразование Фурье.

17.7.1. Содержание метода

Характеристическая функция случайной величины η, представляющей сумму N независимых случайных величин ξ₁, ξ₂,..., ξ_n

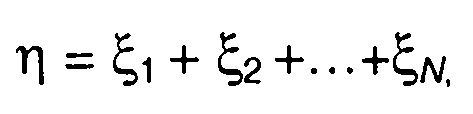(17.94)

имеет вид

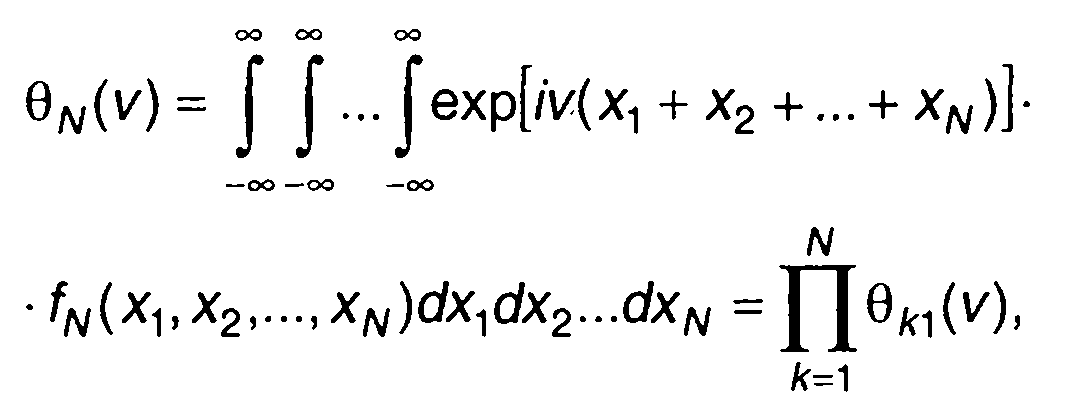(17.95)

где θ_k₁ (v) - характеристическая функция случайной величины ξ_к1.

Если случайные величины имеют одинаковое распределение, например, представляют выборку из одного стационарного случайного процесса, то

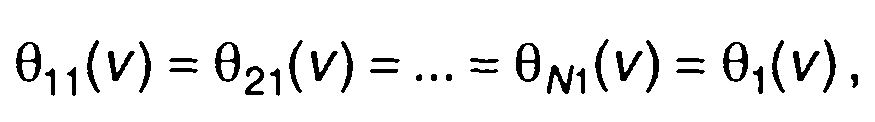(17.96)

(17.95) записывается в виде

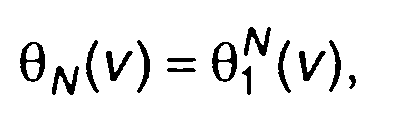(17.97)

где θ₁ (v) - одномерная характеристическая функция случайной величины, определяется выражением

(17.98)

От θ_N(v) можно перейти к соответствующей ПРВ

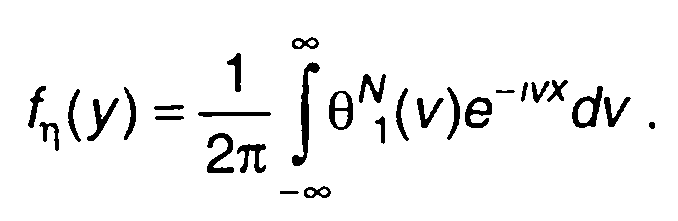(17.99)

Таким образом, чтобы получить ПРВ суммы N независимых случайных величин, имеющих одинаковое распределение, необходимо получить характеристическую функцию одной случайной величины, возвести ее в N-ную степень и найти соответствующее преобразование Фурье.

Рассмотрим пример нахождения ПРВ суммы независимых случайных величин с помощью характеристической функции. Определим ПРВ суммы выборочных значений гауссовского случайного процесса на выходе квадратичного детектора.

17.7.2. ПРВ суммы независимых выборочных значений случайного процесса с обобщенным релеевским распределением

Случайный процесс, представляющий смесь гармонического сигнала и узкополосного шума с нормальным распределеньем, имеет огибающую, распределение которой подчиняется обобщенному закону Релея (разд. 19)

(17.100)

где А - амплитуда сигнала; σ - эффективное значение шума; l₀(х) - модифицированная функция Бесселя первого рода.

Обозначив u/σ = х, А/σ = q, выражение для ПРВ огибающей будем рассматривать в виде

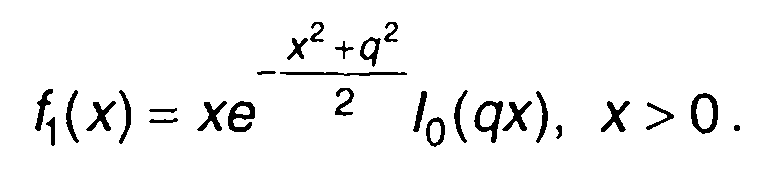(17.101)

Случайный процесс подается на квадратичный детектор с характеристической

(17.102)

Плотность распределения вероятности случайного процесса, выделяемого на выходе детектора, описывается выражением (разд. 15)

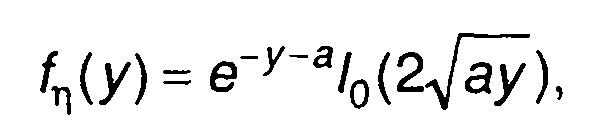(17.103)

где а = q²/2.

Получим ПРВ суммы N независимых выборочных значений случайного процесса, ПРВ которого описывается (17.103). Такая задача возникает при описании процесса накопления при некогерентной обработке принимаемых колебаний.

Характеристическая функция, соответствующая ПРВ (17.103),

определяется выражением

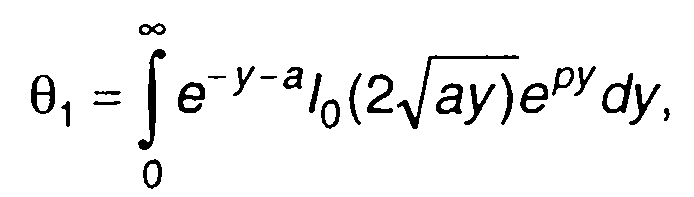(17.104)

где р = iv.

Решение интеграла (17.104) имеет вид [35]

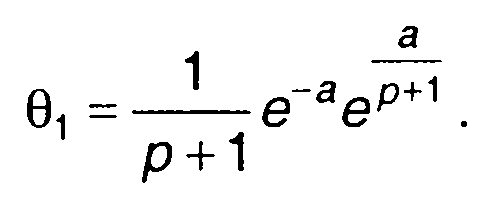(17.105)

Характеристическая функция суммы N независимых выборочных значений определяется (17.97)

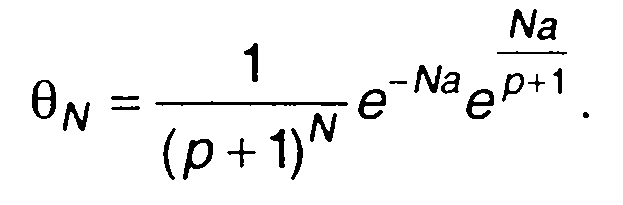(17.106)

Преобразование Фурье характеристической функции θ_N дает ПРВ суммы N независимых случайных величин

(17.107)

При а = 0

(17.108)

Графики f_η(z) при значениях а, равных 0, 1 и 2, приведены на рис. 17.1.

Выражение для f_η(z) можно представить в виде ряда Грама - Шарлье (разд. 15).

Начальные моменты распределения случайной величины, имеющей характеристическую функцию, описываемую (17.106), определяются как

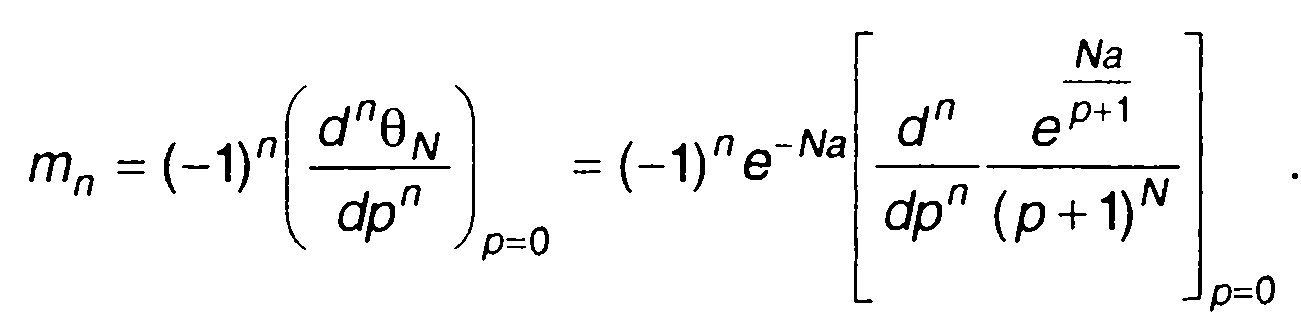(17.109)

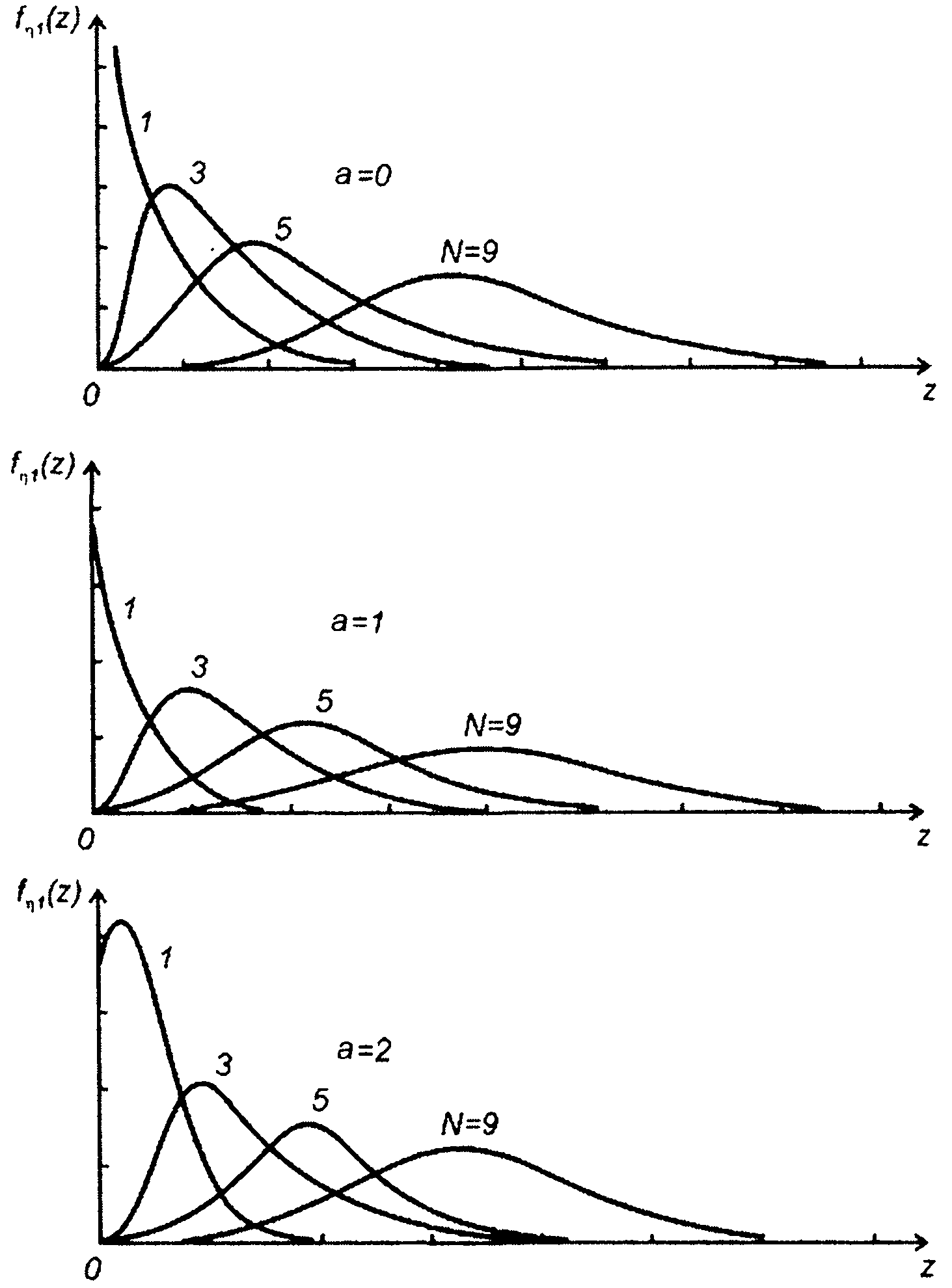
Рис.17.1

Из (17.109) получим

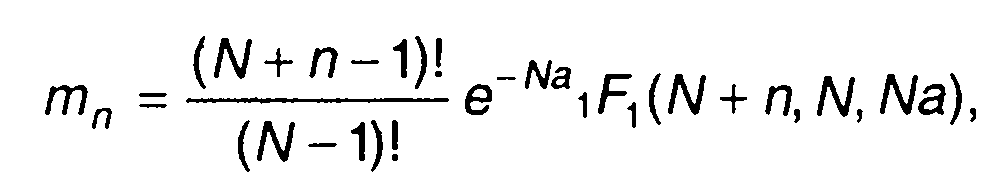(17.110)

или

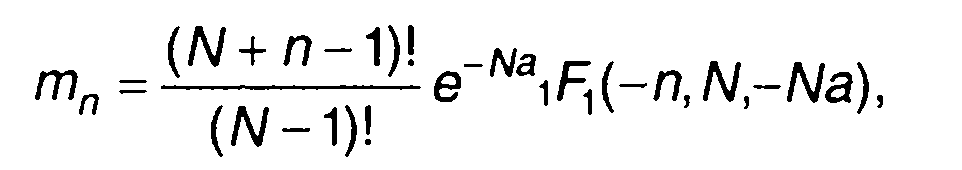(17.111)

где ₁F₁()- гипергеометрическая функция.

Первые начальные моменты распределения вероятностей равны

(17.112)

Центральные моменты распределения вероятностей находятся из (15.18) с учетом (17.112)

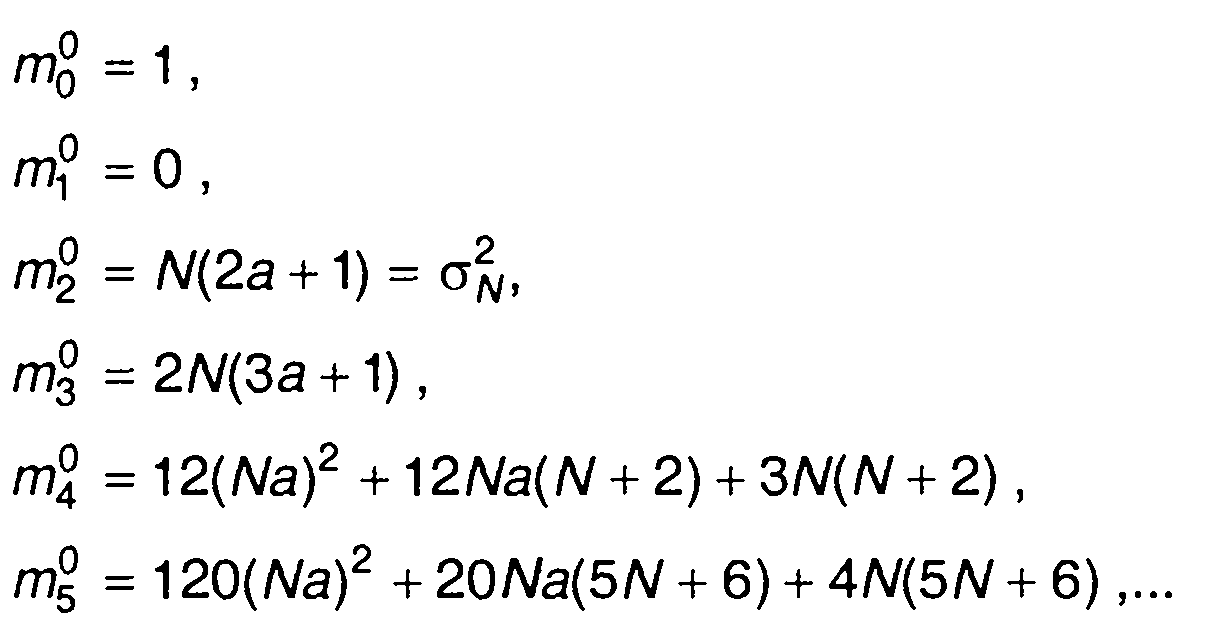(17.113)

Коэффициенты ряда Грама-Шарлье определяются через центральные моменты следующими выражениями:

(17.114)

Ряд Грама-Шарлье для f_η(z) запишется в виде

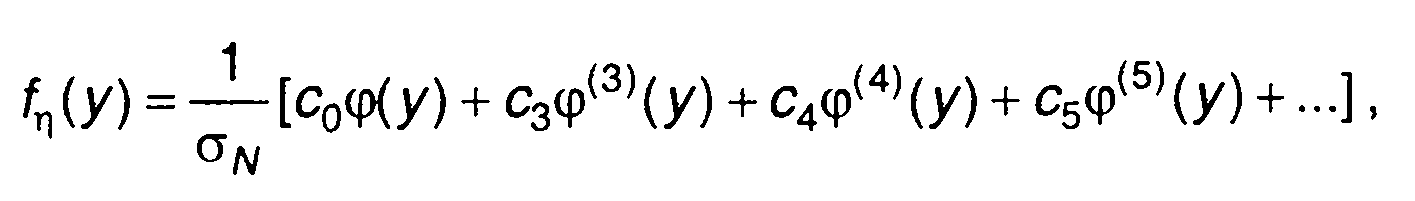(17.115)

где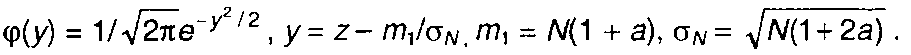

Записанное выражение позволяет определить степень приближения f_η(z) к нормальной ПРВ. Выражение(17.115) показывает, что при увеличении числа N вес второго и последующих членов в общей сумме уменьшается: все коэффициенты разложения стремятся к нулю, за исключением с₀. При достаточно большом значении N распределение случайной величины стремится к нормальному

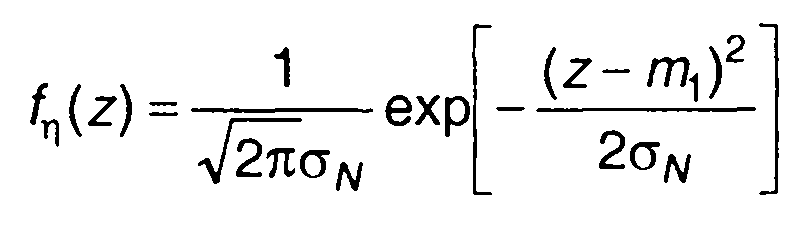
или (17.116)

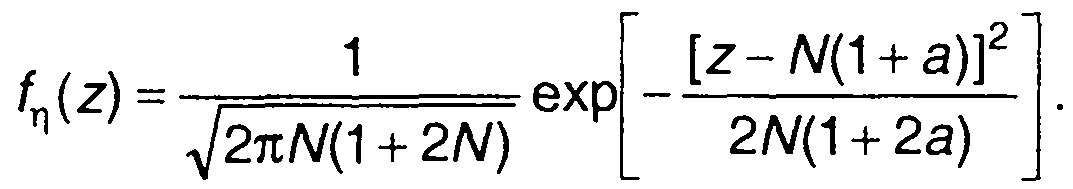
Вывод о приближении распределения суммы случайных величин к нормальному иллюстрируют и графики на рис. 17.1.

Плотность распределения вероятности суммы N независимых случайных величин, имеющих ПРВ, описываемую (17.107), можем представить также в виде ряда Лагерра. С учетом равенств:

выражение для f_η (z) получим в виде

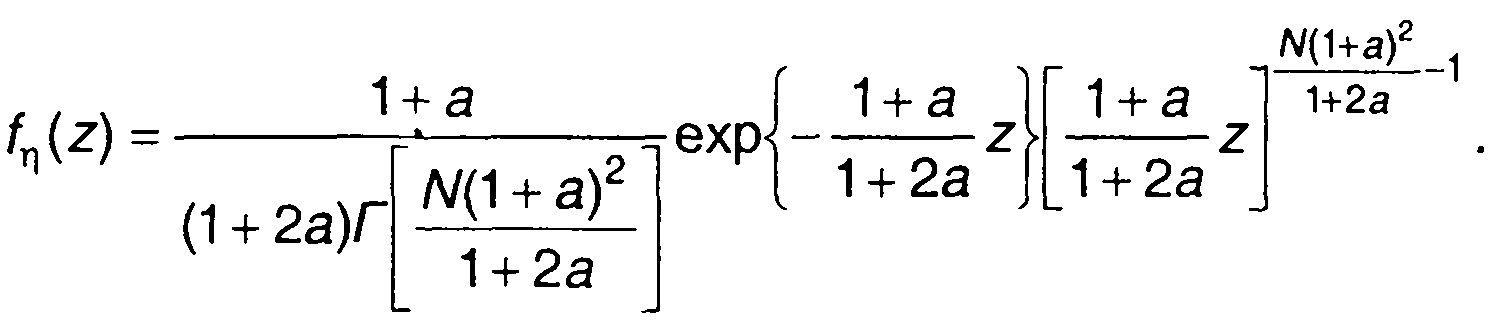(17.117)

При а = 0 имеем m₁ = N, σ_N² = N.

Подставляя (17.117) в (15.78), получим

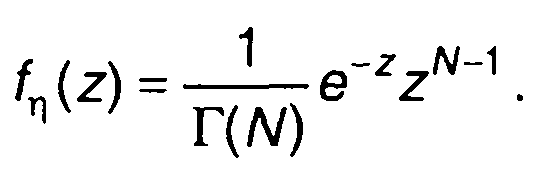(17.118)

При рассмотрении суммы независимых случайных процессов, имеющих распределение, отличное от нормального, необходимо иметь в виду центральную предельную теорему теории вероятностей. В соответствии с ней при достаточно общих условиях распре-

деление центрированных и нормированных случайных величин с увеличением числа слагаемых стремится к нормальному, независимо от законов распределения исходных случайных величин. Применительно к случайным процессам это означает, что распределение суммы независимых выборочных значений одного или нескольких случайных процессов при увеличении числа слагаемых стремится к нормальному. Примером такого приближения служит полученное выражение (17.115) для рассмотренных в п. 17.7.2 условий.

17.7.3. Характеристика помехоустойчивости системы обнаружения сигналов с накоплением

При обнаружении импульсных сигналов на фоне шума с целью повышения помехоустойчивости системы используется накопление импульсов. Накопление может рассматриваться как суммирование амплитуд принимаемых коротких импульсов, поступающих на выход устройства обработки в определенные моменты времени.

При наличии на входе системы помехи (случайного процесса - шума) ПРВ колебания будет описываться функциями (рис. 17.2): f₁⁽^c⁺ⁿ⁾(x) - когда принимается сигнал, и f₁⁽ⁿ⁾(x)- когда сигнал отсутствует.

О наличии сигнала судят с помощью порогового устройства - при превышении значения порога V принимается решение о наличии сигнала, в другом случае - о его отсутствии (рис. 17.2). При обнаружении сигнала возможны два вида ошибок: пропуск сигнала (принимается решение об отсутствии сигнала при его наличии на входе) и ложная тревога (принимается решение о наличии сигнала при его отсутствии на входе). При уменьшении порога уменьшается вероятность пропуска сигнала, но увеличивается вероятность ложной тревоги.

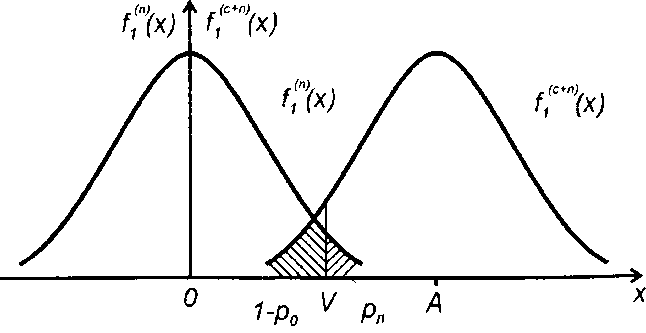
При анализе помехоустойчивости системы обычно рассматриваются вероятность обнаружения сигнала р₀ и вероятность ложной тревоги р_л. Увеличивая значение порога решающего устройства V уменьшаем значения как р_л, так и р₀. Зависимость вероятности обнаружения сигнала от вероятности ложной тревоги и характеризует помехоустойчивость рассматриваемой системы. Чем выше расположен график указанной зависимости при заданном отношении сигнал/помеха на входе, тем выше помехоустойчивость системы. Как указывалось, одним из путей повышения помехоустойчивости системы является метод накопления.

Зависимость р₀(р_п) для системы с накоплением можно получить, если известна ПРВ случайного процесса на выходе накопителя при наличии сигнала на входе и его отсутствии. Определение такой характеристики помехоустойчивости системы является иллюстрацией использования описанных методов анализа случайных процессов при решении одной из задач, поставленных практикой.

При аддитивной помехе в виде гауссовского шума ξ(t) (когерентная обработка) колебание на входе:

где s(t) - сигнал.

Выражения для ПРВ случайного процесса на входе накопителя записывается как:

при наличии сигнала на входе

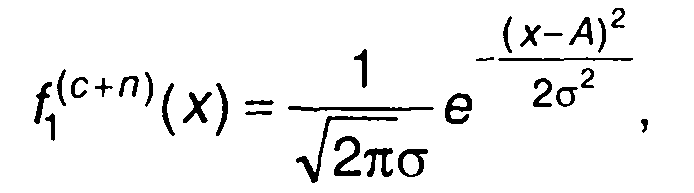(17.119)

в отсутствие сигнала

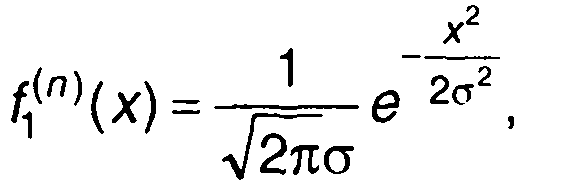(17.120)

где А - амплитуда сигнала на входе; σ² - дисперсия случайного процесса (квадрат эффективного значения) на входе.

Сумма N независимых выборочных значений (случайный процесс на выходе накопителя) имеет также нормальное распределение с математическим ожиданием NA и дисперсией Nσ². Таким образом, ПРВ случайного процесса на выходе накопителя будет описываться выражениями:

при наличии сигнала на входе

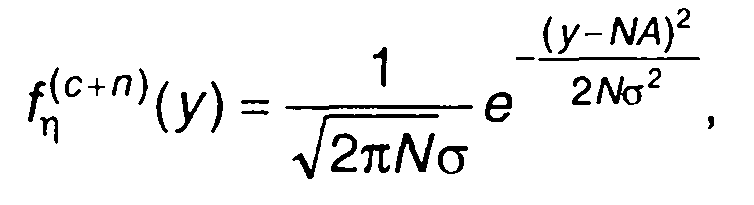(17.121)

в отсутствие сигнала

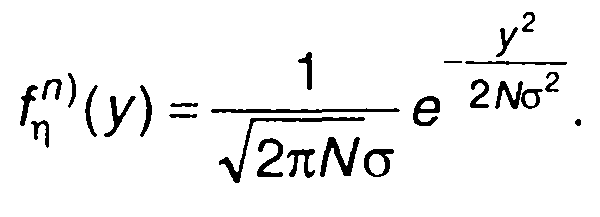(17.122)

Исходя из (17.121) и (17.122) запишем выражения для вероятности обнаружения сигнала:

(17.123)

вероятности ложной тревоги:

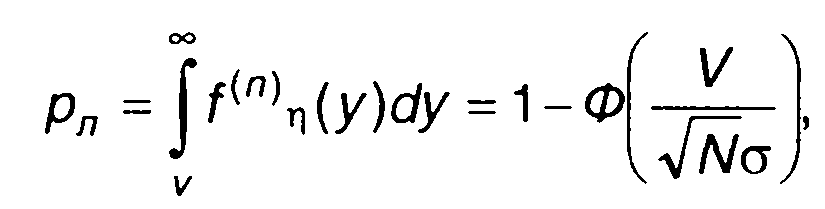(17.124)

где V - заданный порог; Ф(х) - табличная функция нормального распределения.

Из (17.123) и (17.124) получим зависимость р₀(р_п) в явном виде

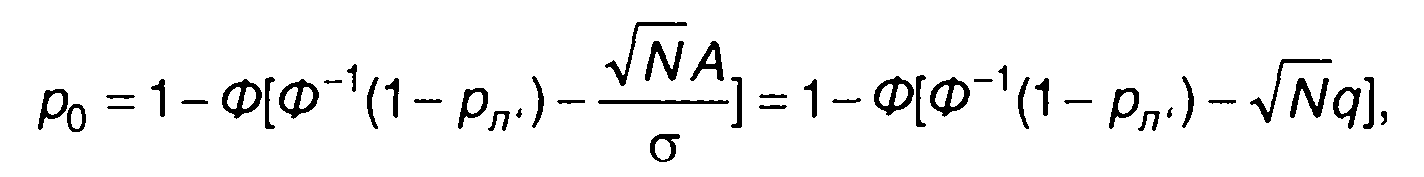(17.125)

где Ф^-1(х) - функция обратная Ф(х), q = А/σ.

Графики p_о(p_л) при отношении сигнал/шум q = 1 и некоторых значений N приведены на рис. 17.3.

При N = 1

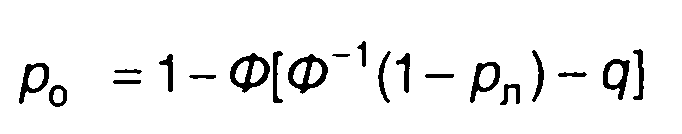(17.126)

Сравнение (17.125) и (17.126) дает основание рассматривать когерентное накопление как улучшение отношения сигнал/шум

в √N раз.

При некогерентной обработке принимаемых колебаний, накоплении на выходе детектора, ПРВ случайного процесса на выходе накопителя описывается (17.107) или (17.108)

Рис. 17.3

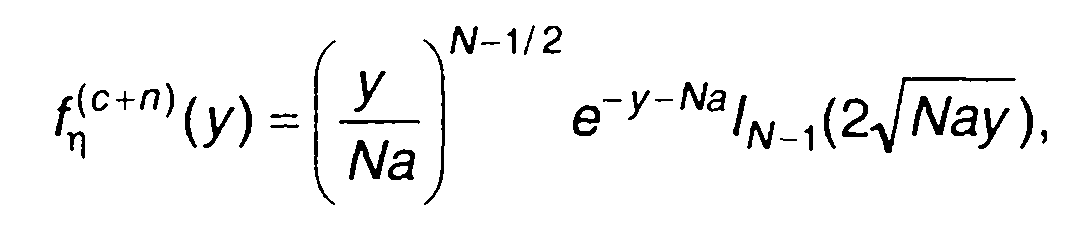(17.127)

(17.128)

где a =q²/2, q =A/σ - отношение сигнал/шум.

При заданном уровне V на выходе накопителя выражение для вероятности ложной тревоги запишется в виде

(17.129)

Вводя неполную гамма-функцию

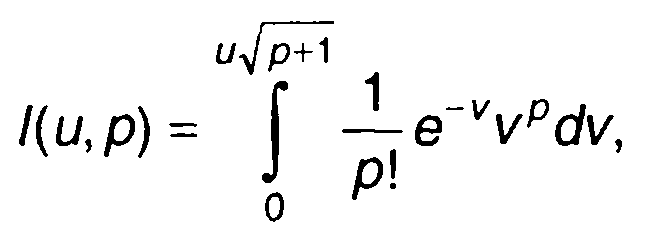(17.130)

выражение для р_л запишем в виде

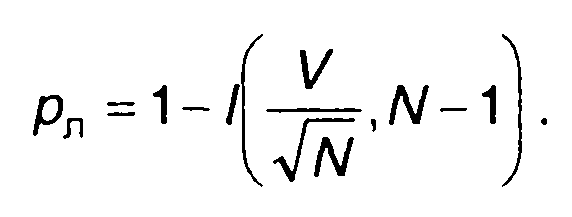(17.131)

В [35] решение (17.129) получено в виде ряда

Рис.17.5

Рис. 17.4

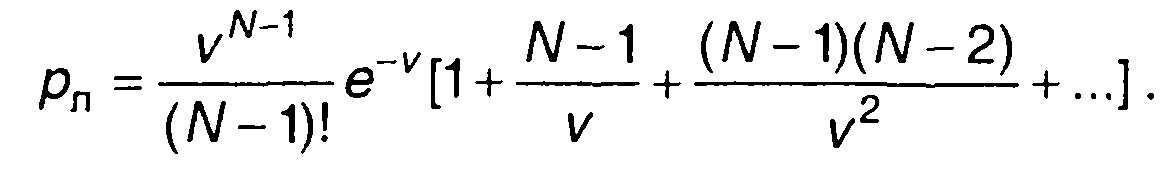(17.132)

Вероятность обнаружения сигнала определяется с учетом (17.127) как

(17.133)

Решение (17.135) получено в виде ряда [35]

(17.134)

Выражение (17.131) и (17.134) определяют зависимость р₀(р_п). Графики указанной зависимости для некоторых значений N приведены на рис. 17.4.

Как указывалось, накопление эквивалентно улучшению отношения сигнал/шум. Однако в отличие от предыдущего случая это улучшение будет различным в разных точках зависимости р_о(р_л). Его можно оценить, сравнивая зависимости р_о(р_п) при заданном значении N и N = 1 (рис. 17.5). Так при q = 1 и р_п = 10^-2 накопление при N = 10 эквивалентно улучшению отношения сигнал/шум, равному 1,7; при N = 50 - 2,6; при N = 100 - 3,5.

Раздел 18.

СПЕКТР СЛУЧАЙНОГО ПРОЦЕССА

Спектральный анализ является основой исследования детерминированных сигналов. Это делает целесообразным обращение к методам спектрального анализа и при исследовании случайных процессов. Однако особенности случайных процессов делают невозможным простой перенос методов анализа детерминированных сигналов на случайные процессы. Спектральный анализ случайных процессов несет особенности, которые требуют отдельного рассмотрения.

18.1. Понятие спектральной плотности мощности случайного процесса

Рассматривая реализацию случайного процесса как функцию времени, формально для нее можем записать преобразование Фурье. Однако чаще всего такое преобразование не существует, по крайней мере, для непрерывных случайных процессов ξ,(t) не выполняется условие абсолютной интегрируемости

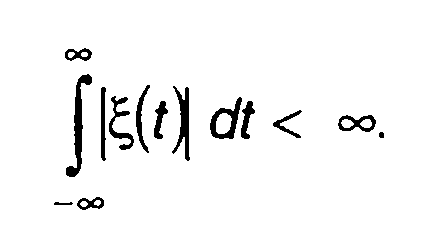(18.1)

Преобразование Фурье применимо только к такой характеристике случайного процесса, для которой условие интегрируемости абсолютного значения выполняется.

Выделим отрезок реализации случайного процесса

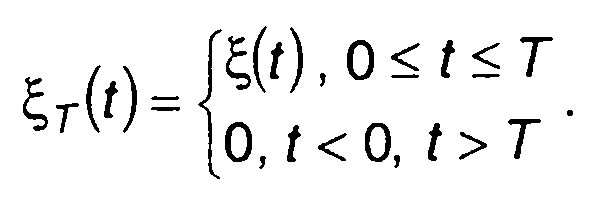(18.2)

Отрезок ξ(t) представляет функцию времени на интервале [0,Т]. Если для нее существует преобразование Фурье

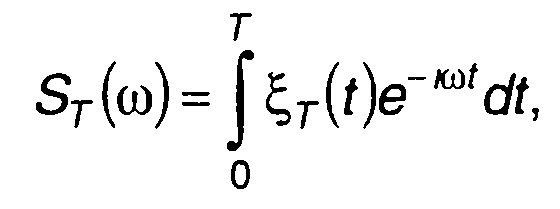(18.3)

то применительно к ξ_T(t) и S_T(ω) можем записать равенство Парсеваля

(18.4)

Поделив левую и правую части равенства (18.4) на длину рассматриваемого интервала времени Т, запишем

(18.5)

Каждая часть равенства (18.5) описывает среднюю мощность случайного процесса на интервале Т. При T→∞ в правой части равенства под знаком интеграла будет спектральная плотность мощности случайного процесса. Обозначим ее N(ω). Тогда (18.5) при T→∞ запишется в виде

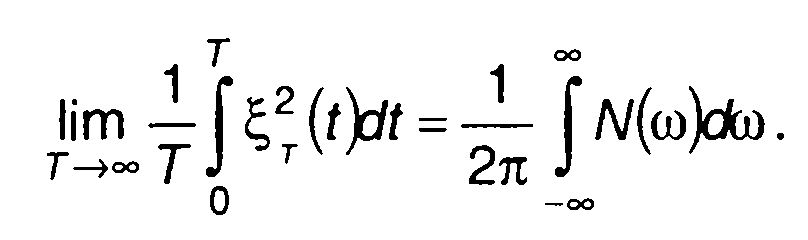(18.6)

Спектральная плотность мощности характеризует распределение мощности случайного процесса по частоте, имеет четкое физическое содержание, определяется как аналитически, так и аппаратурно. Во временной области спектральной плотности мощности соответствует по Фурье корреляционная функция случайного процесса.

18.2. Соотношение между спектральной плотностью мощности и корреляционной функцией случайного процесса

Рассмотрим центрированный случайный процесс ξ(t) Выражение для его спектральной плотности мощности с учетом (18.3) запишется в виде

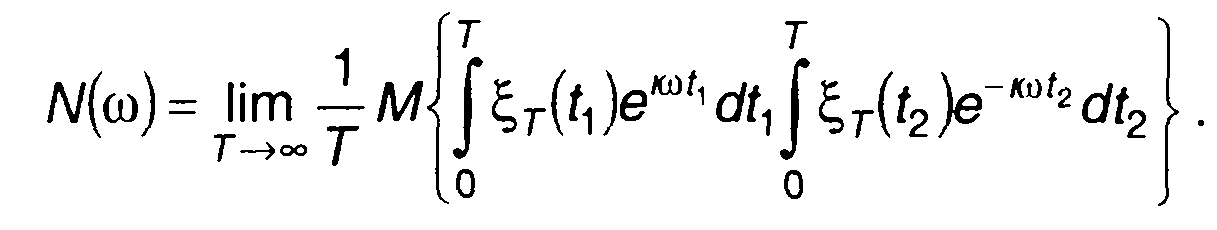(18.7)

Преобразуем (18.7)

(18.8)

где R(t₁,t₂)~ корреляционная функция случайного процесса.

Для стационарного случайного процесса

выражение (18.8) запишется в виде

(18.9)

В выражении

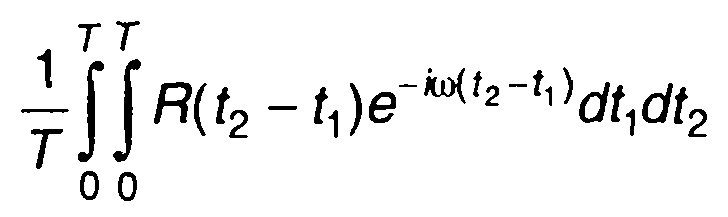(18.10)

произведем замену переменных t₁ и t₂ на t = t₁ и τ = t₂-t₁ (18.10) представим в виде

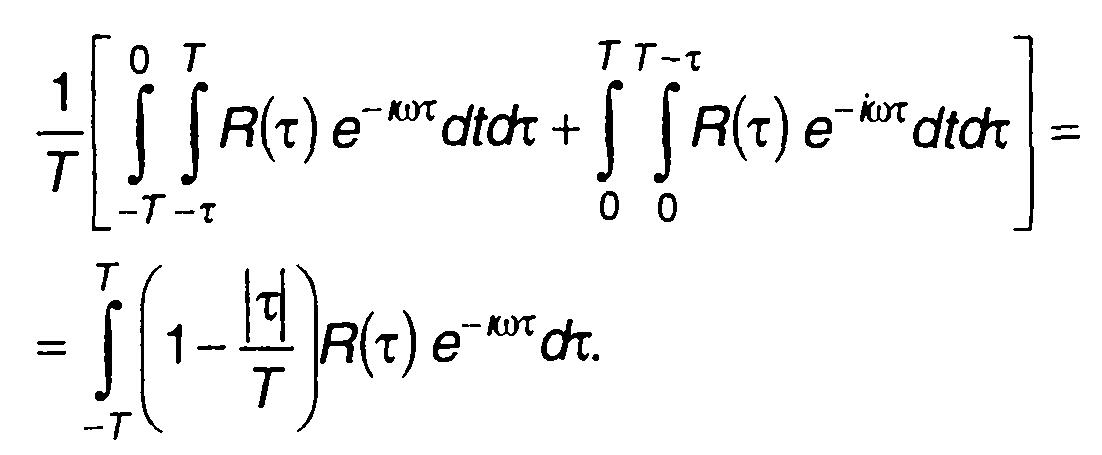(18.11)

Переходя к пределу, из (18.9) с учетом (18.11) получим

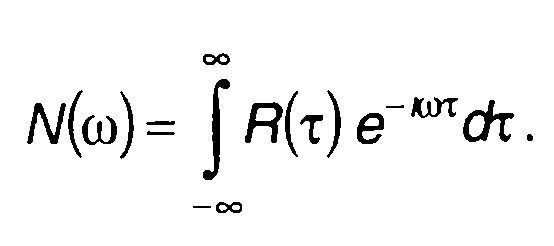(18.12)

Таким образом, спектральная плотность мощности определяется как преобразование Фурье корреляционной функции случайного процесса. Обратное преобразование Фурье позволяет перейти от спектральной плотности мощности случайного процесса к его корреляционной функции

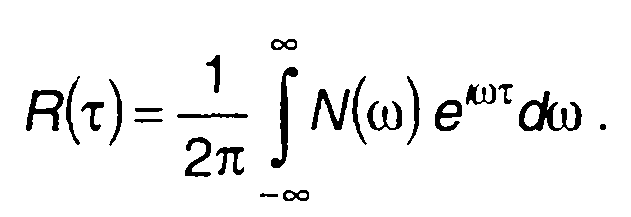(18.13)

Выражения (18.12) и (18.13), связывающие спектральную плотность мощности и корреляционную функцию случайного процесса, называются соотношениями Хинчина-Винера. При их выводе не оговаривались ограничения, накладываемые на случайные процессы. Однако следует иметь в виду, что преобразование Фурье возможно только для абсолютно интегрируемой функции, т. е. когда выполняется неравенство

Указанное условие выполняется только для центрированного случайного процесса - математическое ожидание которого равно нулю. Функция же N(ω) может быть спектральной плотностью

мощности случайного процесса только тогда, когда она является абсолютно интегрируемой

С учетом четности R(τ) и N(ω) выражения для них можно записать в виде

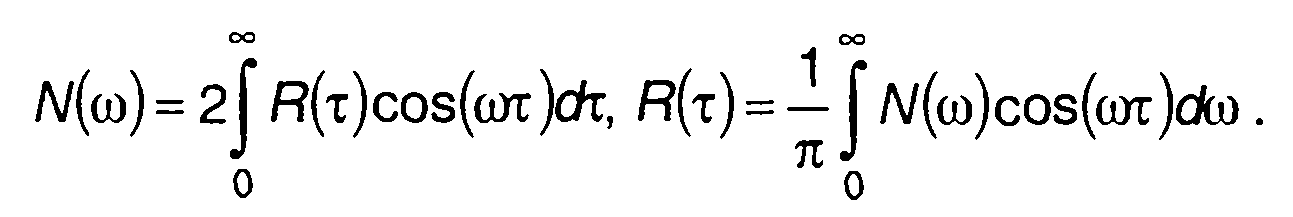(18.14)

При использовании (18.14) полезно учитывать свойства косинус- преобразования Фурье.

Мощность случайного процесса определяется R(0), из (18.14) получим

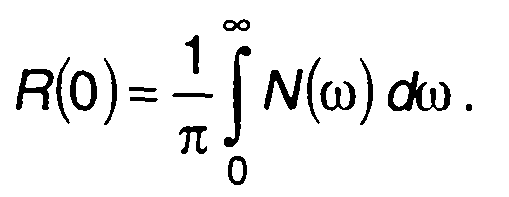(18.15)

Она численно равна площади под кривой спектральной плотности мощности с коэффициентом 1/2π.

Спектральная плотность мощности случайного процесса при ω = 0 определяется выражением

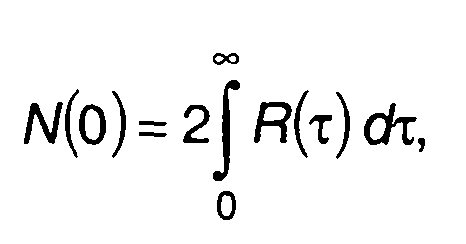(18.16)

т.е. равна площади под кривой корреляционной функции.

Соотношения (18.14) позволяют получить спектр случайного процесса, зная корреляционную функцию, или по спектру определить корреляционную функцию случайного процесса. Исходной при описании случайного процесса может быть как одна, так и другая характеристика.

Нормированная величина спектральной плотности мощности

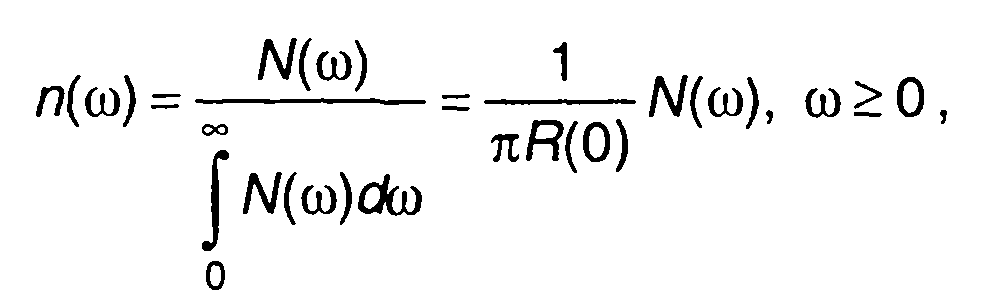
обладает свойствами ПРВ частоты. Величину

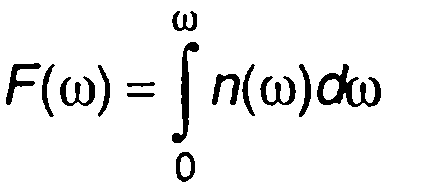
можно рассматривать как ФРВ частоты, она обладает свойствами ФРВ

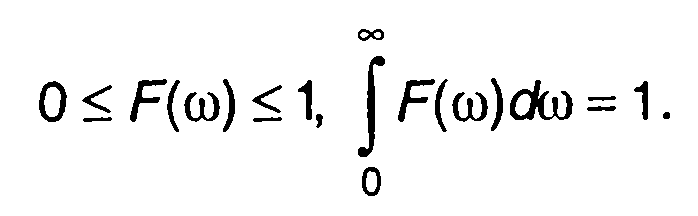
Величина n(ω)dω представляет вероятность того, что случайный процесс обладает средней мощностью 1/π*N(ω)dω в полосе частот [ω₁ω+dω]

Рассматривая спектральную плотность мощности как ПРВ (без учета коэффициента), корреляционную функцию можно отождествить с характеристической функцией

<16 17 181920 21 22 >

Дата добавления: 2015-12-16; просмотров: 880;