ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 17 страница

Исходя из приведенных определений получим следующее соот­ношение между корреляционной и ковариационной функциями

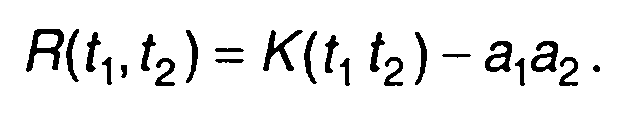(16.12)

При t₁ = t₂= t (16.12) описывает дисперсию случайного процесса в выбранный момент времени R(t, t) = σ² .

Нормированная величина центрального момента второго порядка

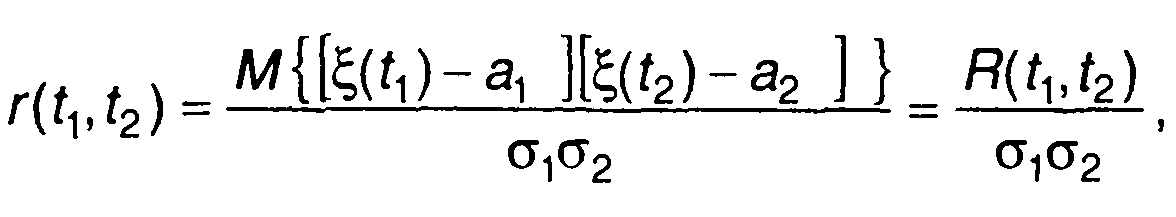(16.13)

где а_к,σ_к- математическое ожидание и дисперсия случайного про­цесса в /с-й момент времени, называется нормированной корреля­ционной функцией или коэффициентом корреляции случайного процесса.

Корреляционная функция в общем случае зависит от двух мо­ментов времени t₁ и t₂, для стационарного случайного процесса - только от их разности τ = t₂- t_1t т. е. R(t,t + τ) = R(τ). Для стационар­ного случайного процесса R(τ) = К(τ) - а².

Нормированная корреляционная функция стационарного про­цесса равна

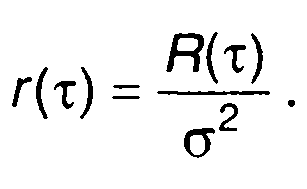(16.14)

Она является четной функцией (рис. 16.3) r(τ) = r(-τ), имеет максимальное значение при τ = 0, т.е. r(τ) < к(0) = 1, при т→∞ имеем r(τ) →0 .

Вследствие четности R(τ) или r(τ) их графики в дальнейшем приводятся только для т >0.

Корреляционная функция эргодического случайного процесса может определяться усреднением по времени произведения значе­ний одной реализации случайного процесса, взятых в моменты времени, смещенные .один относительно другого на интервал вре­мени т

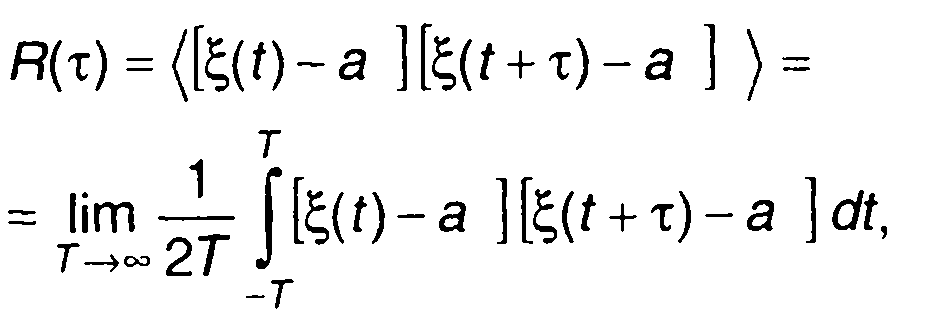(16.15)

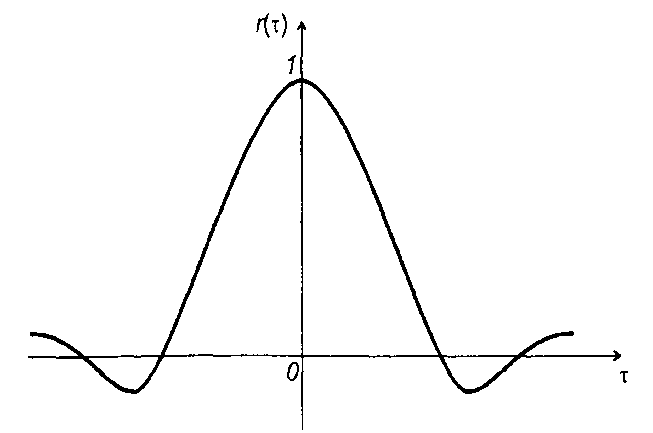
Рис. 16.3

где символ усреднения по времени.

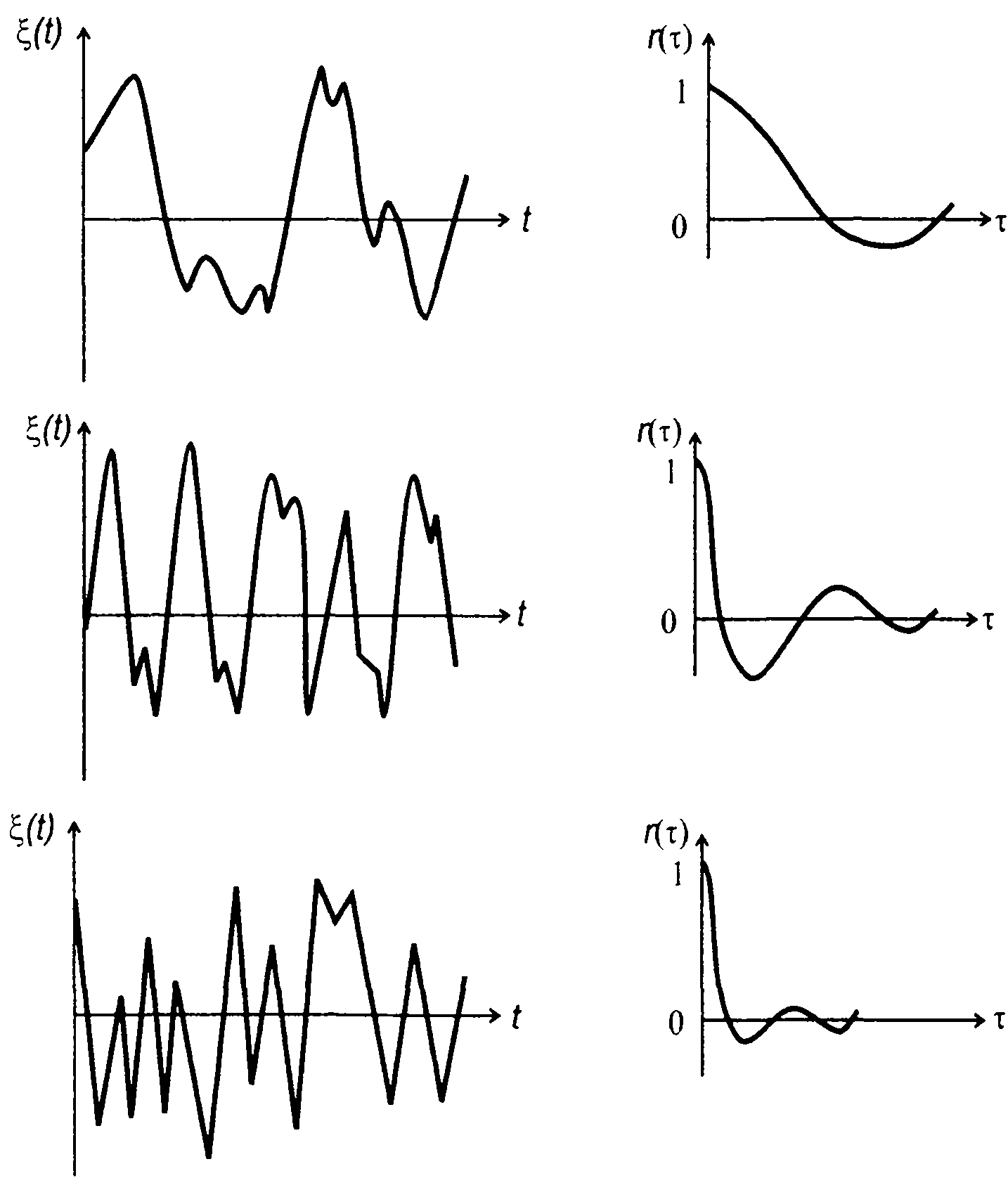
Корреляционная функция является одной из основных характе­ристик случайного процесса, широко используемых при его описа­нии и анализе. Она определяет степень статической связи между значениями случайного процесса, взятыми в момент времени t₁ и t₂; для стационарных случайных процессов - в моменты времени, разнесенные на интервал т. Сказанное может быть проиллюстри­ровано примерами реализаций случайных процессов и графиками их корреляционных функций, выполненными в одном масштабе, на рис. 16.4. Чем более осциллирующий характер имеет реализация, тем уже корреляционная функция.

Ширина корреляционной функции может быть оценена интерва­лом корреляции.

16.2.2. Интервал корреляции

Для каждой корреляционной функции можно определить такое минимальное значение смещения во времени τ_к, при котором аб­солютное значение нормированной корреляционной функци будет меньше заданной величины (близко к нулю). Значения случайного процесса ξ(t) и ξ(t + τ_k) в этом случае можно считать некоррели­рованными; величину τ_к называют интервалом корреляции. Иными

словами, интервал корреляции представляет длину наибольшего интервала времени, на котором корреляционная функция ещё име­ет значение, существенное для решаемой задачи.

Используют различные определения интервала корреляции τ_к,

наиболее часто - следующие.

• Интервал корреляции, определяемый по заданному абсолют­ному значению нормированной корреляционной функции (рис. 16.5,а)

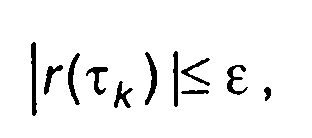
где в - заданное значение (например, ε = 0,05).

• Интервал корреляции, определяемый интегралом от нормиро­ванной корреляционной функции или её абсолютного значения (рис. 16.5,6)

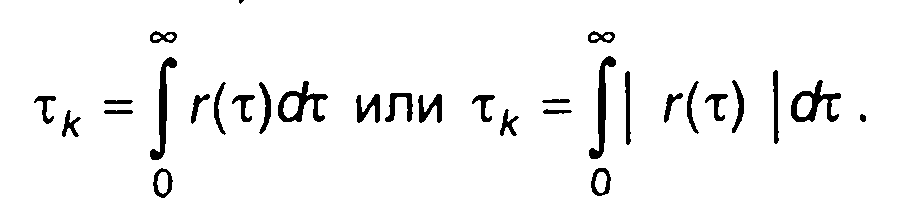
При таком определении интервал корреляции численно равен основанию прямоугольника, высота которого равна максимальному значению нормированной корреляционной функции т(0) = 1, а пло­щадь равна площади под кривой r(т) или | r(τ) | (при т > 0).

• Интервал корреляции, определяемый интегралом от квадрата нормированной корреляционной функции (рис. 16.5,в)

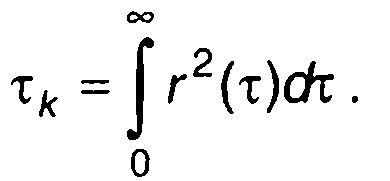
Значения τ_к, получаемые из приведенных определений, близки друг к другу, выбор же определения, как правило, диктуется удобст­вом при решении конкретной задачи, где понятие интервала корре­ляции используется.

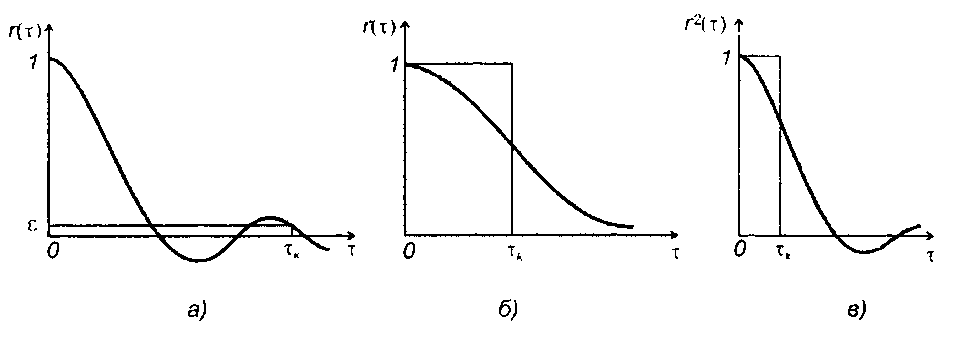
Рис. 16.5

16.2.3. Корреляционная функция телеграфного сигнала

В качестве примера корреляционной функции случайного дис­кретного процесса приведем корреляционную функцию телеграф­ного сигнала (разд. 15). Случайный процесс принимает значения 1 или -1. Переход от одного значения к другому происходит скачком (рис. 16.6,а). Вероятность того, что в интервале времени τ проис­ходит k скачков, описывается ПРВ Пуассона.

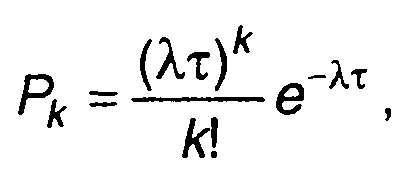(16.16)

где λ - среднее число скачков в единицу времени.

Корреляционная функция телеграфного сигнала в соответствии с (16.11) определяется выражением

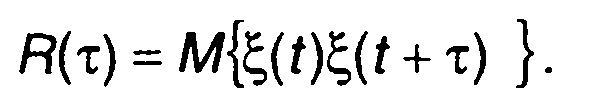(16.17)

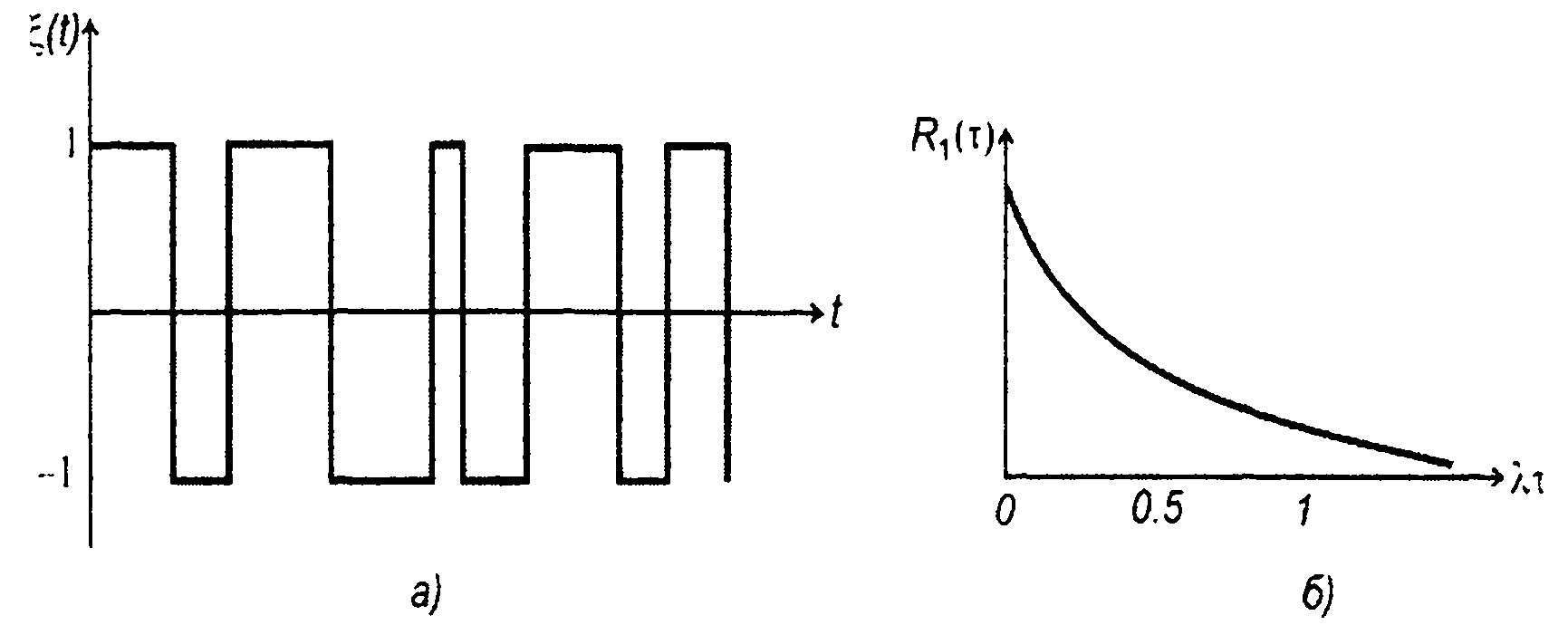
Рис. 16.6

Произведение ξ(t)ξ(t+ т) может быть равно либо 1, либо -1, в

зависимости от того, будет ли выполняться равенство ξ(t) = ξ(t + T) или ξ(t) =-ξ{t + τ). Равенство ξ(t) = ξ(t + т) означает, что на интер­вале т произошло четное число перемен знаков. Вероятность тако­го события

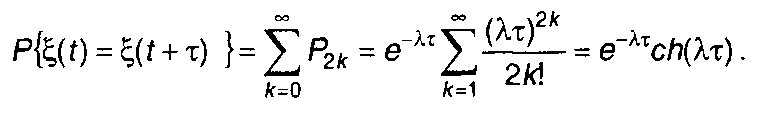(16.18)

Равенство ξ{t) =-ξ{t + т) означает, что на интервале г произош­ло нечетное число перемен знаков. Вероятность такого события

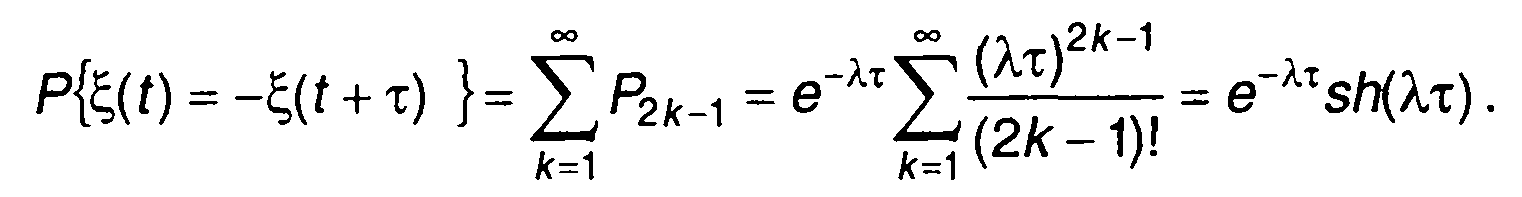(16.19)

С учетом (16.18) и (16.19) выражение для корреляционной функ­ции получим в виде

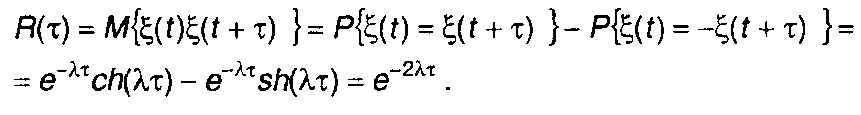
Равенство получено для т ≥ 0 . Учитывая четность корреляцион­ной функции, для всех значений т запишем

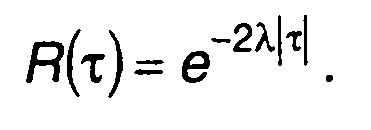(16.20)

График корреляционной функции телеграфного сигнала приве­ден на рис. 16.6,6.

16.3. Многомерное распределение вероятностей гауссовского процесса

В качестве примера л-мерных характеристик распределения случайного процесса приведем характеристики гауссовского про­цесса: двумерные и в общем случае л-мерные ПРВ и ФРВ.

16.3.1. Двумерные ПРВ и ФРВ гауссовского процесса

Двумерная ПРВ стационарного гауссовского процесса для мо­ментов времени t₁ и t₂ = t₁+т описывается выражением

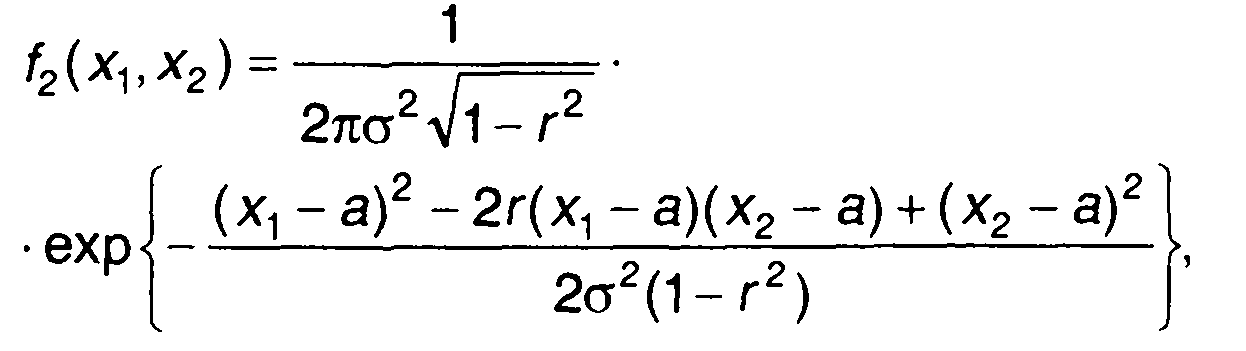(16.21)

где а, σ², r - математическое ожидание, дисперсия и нормирован­ная корреляционная функция случайного процесса.

Как следует из (16.21), двумерная ПРВ определяется двумя ве­личинами: математическим ожиданием а и корреляционной функ­цией R( т) = σ²r(т), где т = t₂ - t₁; для центрированного случайного

процесса - только корреляционной функцией.

При расчете f₂(x₁, х₂) удобнее перейти к нормированным вели­чинам и рассматривать функцию

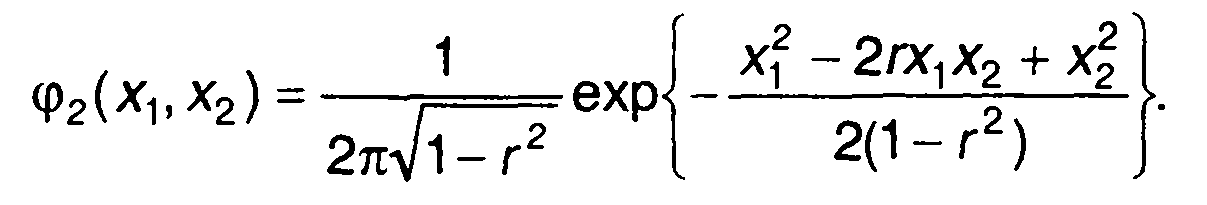(16.22)

Двумерная ФРВ описывается выражением

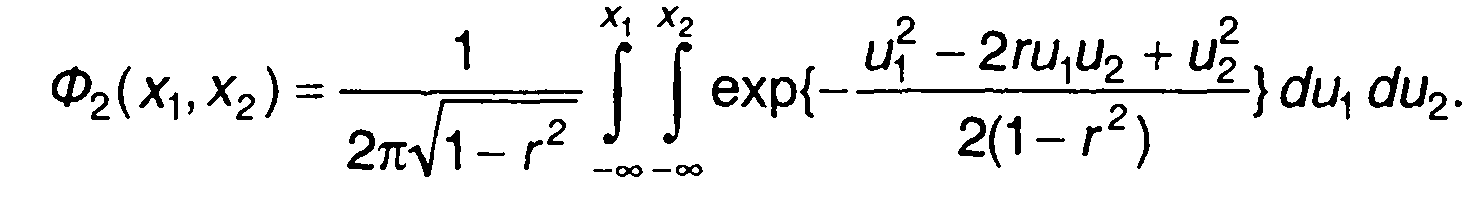(16.23)

Функция (16.23) табулирована.

Для частного случая х₁ = х₂ = 0 из (16.23) получим

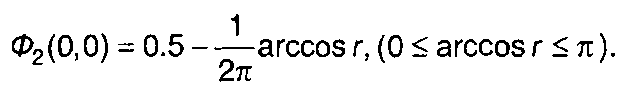(16.24)

При r = О

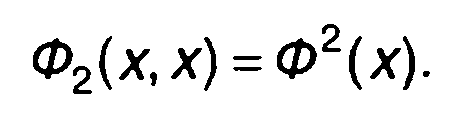(16.25)

При к = 1

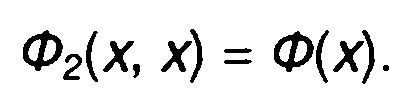(16.26)

Для расчета Ф₂ (х₁, х₂) от (16.23) удобнее перейти к несколько иному выражению. Производя в (16.23) замену переменных

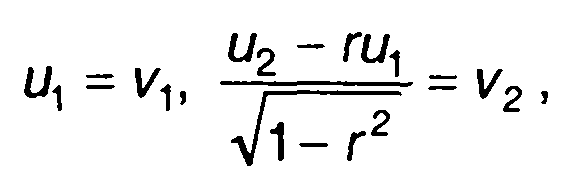(16.27)

выражение для Ф₂ (х₁, х₂) получим в виде

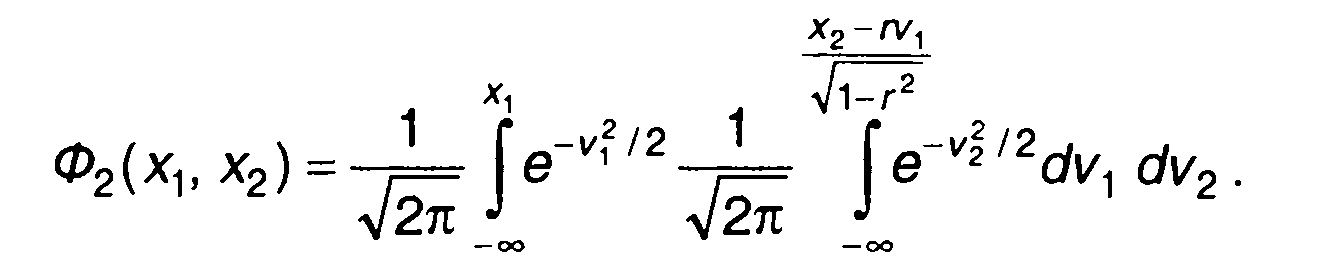(16.28)

Из (16.28) найдем

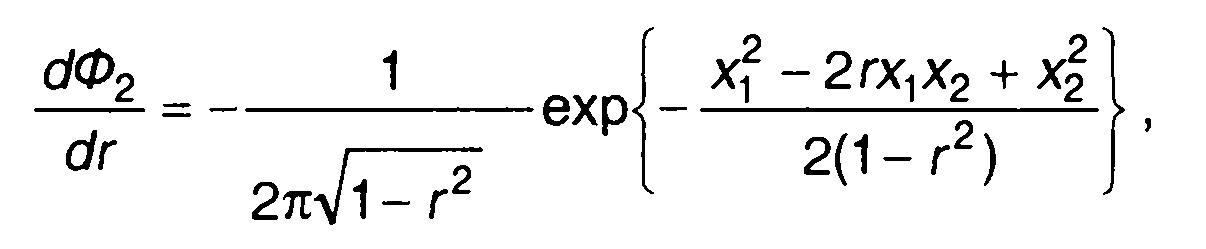(16.29)

что позволяет иметь достаточно простое выражение для расчета двумерной ФРВ гауссовского процесса

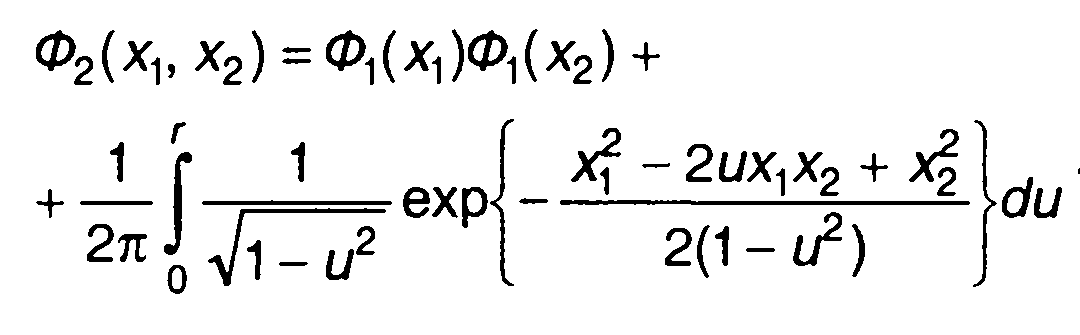(16.30)

Используя (16.29), можно прийти и к другому выражению для расчета двумерной ФРВ

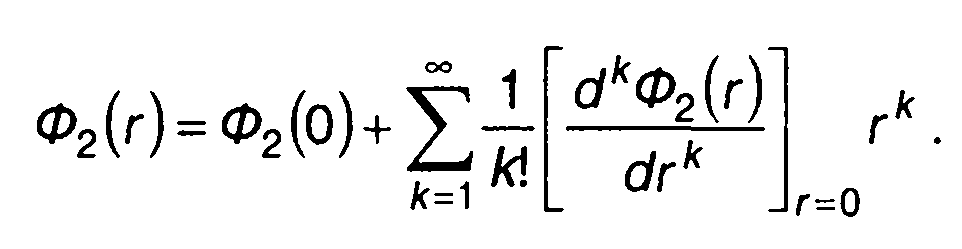(16.31)

Выражения (16.30) и (16.31) позволяют получить достаточно удобные алгоритмы расчета двумерной ФРВ гауссовского случай­ного процесса.

Исходя из двумерной ФРВ, полезно найти выражение для веро­ятности совпадения (или несовпадения) знаков (полярностей) слу­чайного процесса в два выбранных момента времени. Эта вероят­ность функционально связана с корреляционной функцией случай­ного процесса и используется при её экспериментальном опреде­лении (знаковые корреляторы).

Вероятность несовпадения знаков стационарного центрирован­ного случайного процесса определяется выражением

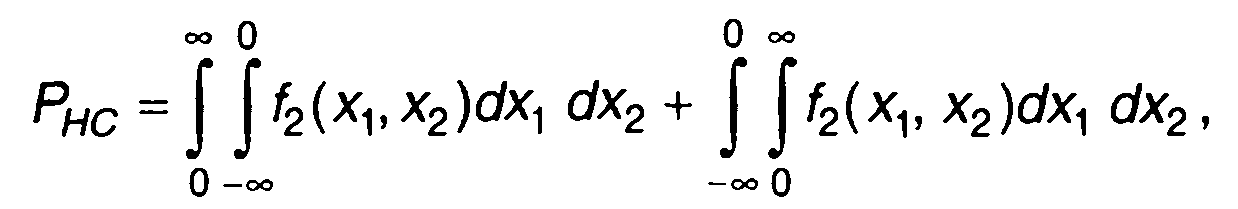(16.32)

где f₂(x₁ х₂) - двумерная ПРВ, описывающая случайный процесс в моменты времени t и t + τ.

Преобразуя (16.32), для гауссовского процесса получаем

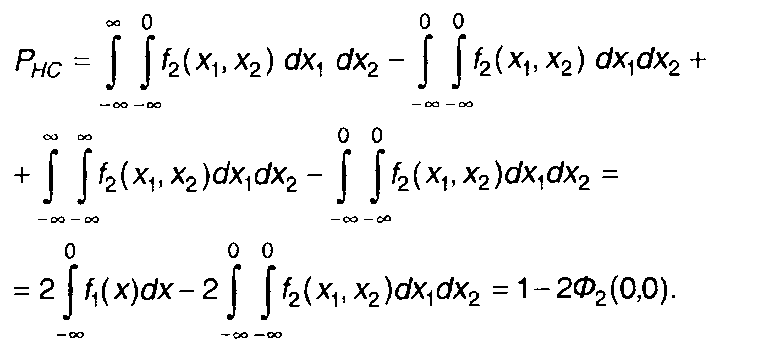(16.33)

С учетом (16.24) запишем

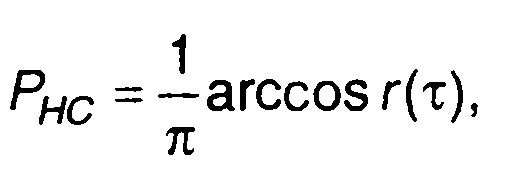(16.34)

где r(т) - нормированная корреляционная функция гауссовского процесса.

Вероятность совпадения знаков значений случайного процесса, разнесенных на интервале т, равна

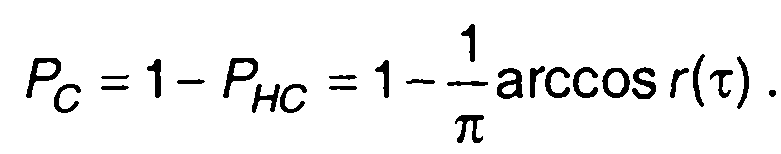(16.35)

Как следует из (16.34) и (16.35), вероятность несовпадения (сов­падения) знаков функционально связана с нормированной корре­ляционной функцией гауссовского процесса. Измеряя эту вероят­ность, можно определить корреляционную функцию гауссовского процесса. В ряде случаев схемная реализация анализатора совпа­дения полярностей случайного процесса оказывается проще, чем множительного коррелятора.

16.3.2. л-мерная ПРВ гауссовского процесса

ПРВ л-го порядка стационарного гауссовского процесса описы­вается выражением

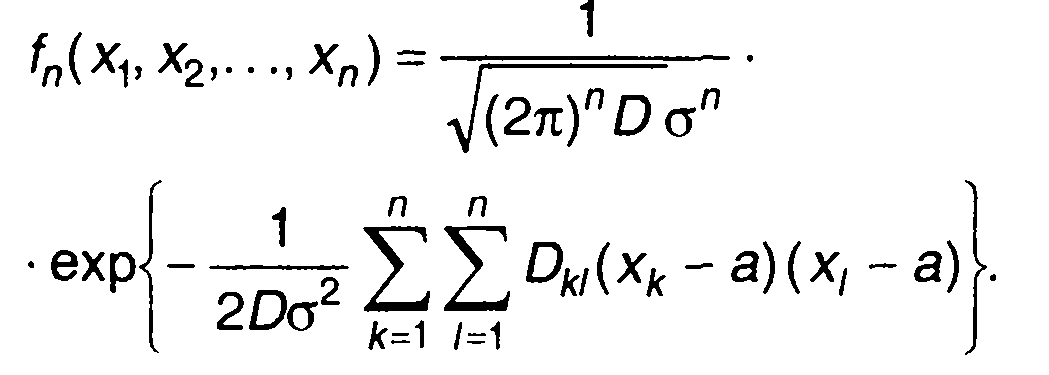(16.36)

В (16.36) обозначено: а, σ² - математическое ожидание и дис­персия случайного процесса; D - определитель n-го порядка

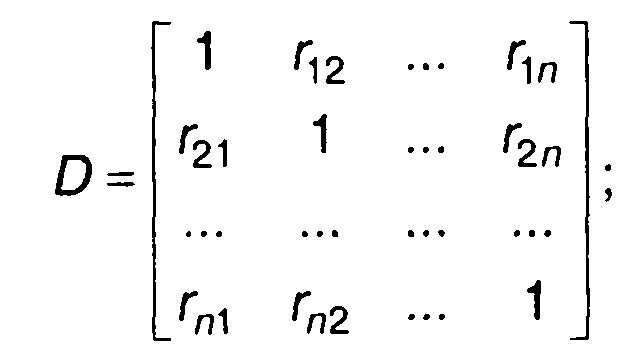(16.37)

r_kl- нормированная корреляционная функция случайного процесса

в моменты времени t_k и t_i D_kl - алгебраическое дополнение эле­мента r_k| в определителе.

Как следует из (16.36) с учетом определителя D, л-мерная ПРВ (ФРВ) гауссовского процесса полностью определяется математиче­ским ожиданием а и корреляционной функцией R(т).

Конкретизируя (16.36) для трехмерной ПРВ, запишем

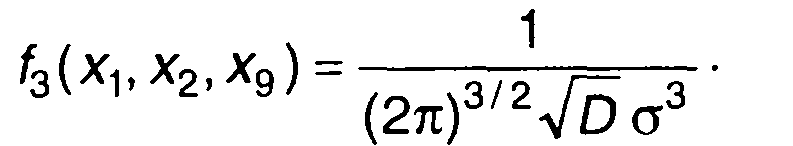
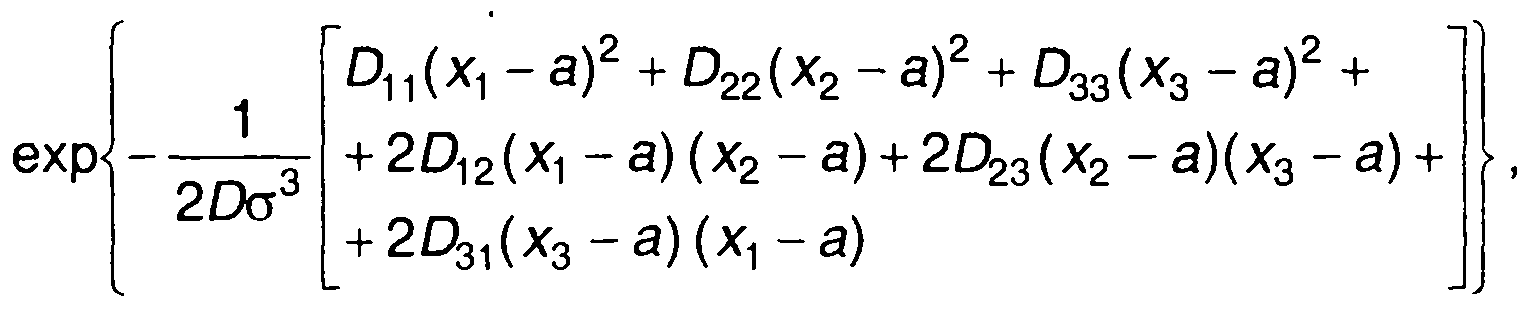(16.38)

где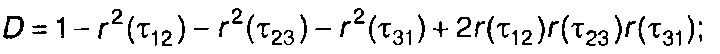

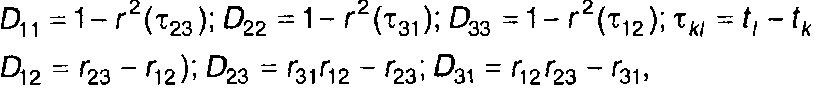(16.39)

а, σ², r(т) - математическое ожидание, дисперсия и нормирован­ная корреляционная функция случайного процесса.

16.4. Разложение двумерной плотности распределения вероятностей в ряд по ортогональным системам функций

При использовании двумерной ПРВ случайного процесса бывает полезным её представление в виде ряда разложения по ортого­нальной системе функций, аналогично тому, как это было сделано в отношении одномерной ПРВ. Такое представление двумерной

ПРВ используется, например, при определении корреляционной функции случайного процесса на выходе нелинейного преобразо­вателя (разд. 22).

В качестве базисных функций выбираются многочлены ортонормированных систем {φ_1n(х₁)} и {φ_2n(x2)}, имеющие в качестве весовой функции одномерную ПРВ случайного процесса f₁(х)

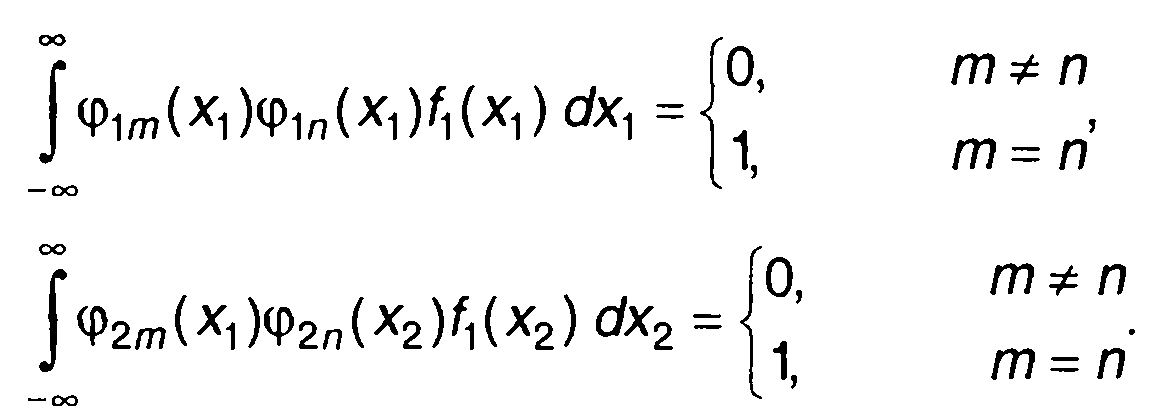(16.40)

Двумерная ПРВ стационарного случайного процесса записыва­ется в виде ряда

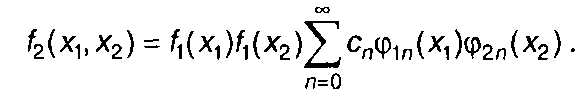(16.41)

С учетом (16.40) коэффициенты с_n в (16.41) определяются вы­ражением

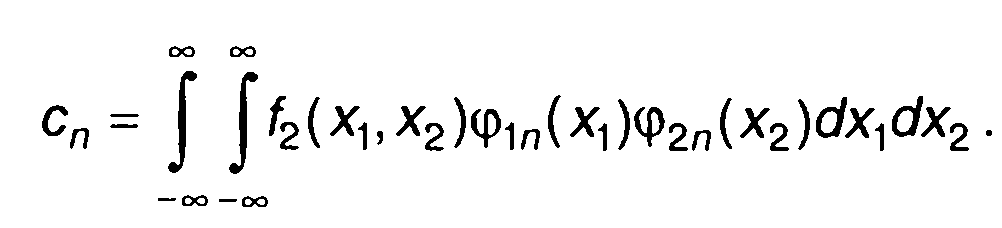(16.42)

Выберем φ₁₀(х₁) = φ₂₀(х₂) = 1, тогда из (16.40) получим

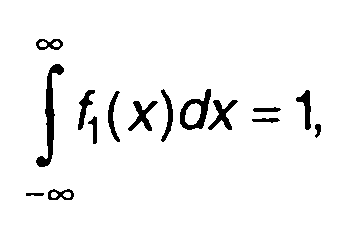(16.43)

что соответствует определению f₁ (х) как ПРВ.

Из (16.42) следует:

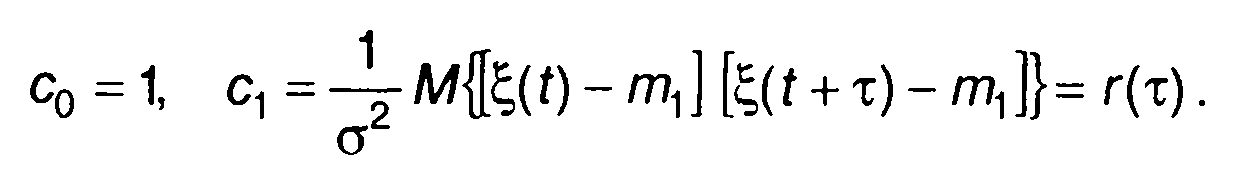(16.44)

В соответствии с (16.42) определяются и другие коэффициенты разложения.

Для гауссовских процессов в качестве базисных функций

целесообразно выбрать нормированные многочлены Эрмита Н_п (х)

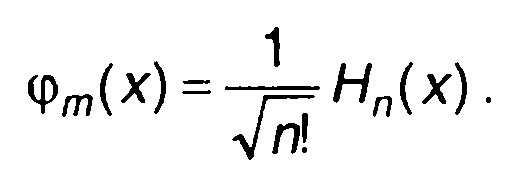(16.45)

В этом случае ряд, в который раскладывается ПРВ, примет вид

(m₁,= 0, σ = 1)

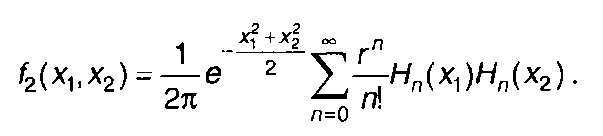(16.46)

Пример использования разложения двумерной ПРВ приведен в разд. 22.

16.5. Условные характеристики распределения вероятностей случайного процесса

Выражение для двумерной ФРВ случайного процесса ξ(t) может быть записано в виде

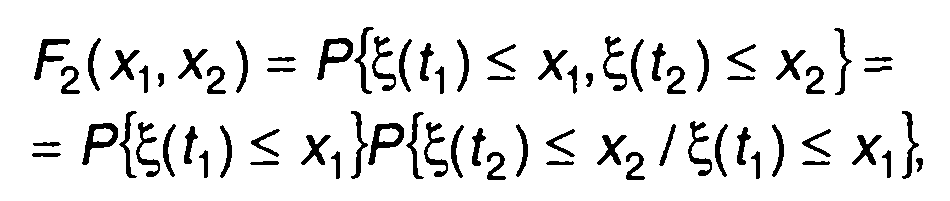(16.47)

где Р(А/В) - условная вероятность.

В правой части (16.47) первый сомножитель представляет од­номерную ФРВ - F₁(x₁). Второй сомножитель - условную ФРВ F₂(x₂/x₁). Таким образом, (16.47) можно записать в виде

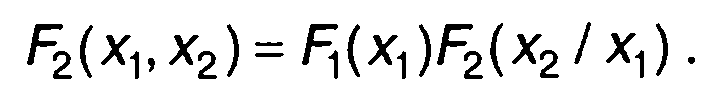(16.48)

Из (16.48) получим выражение для условной ФРВ случайного процесса

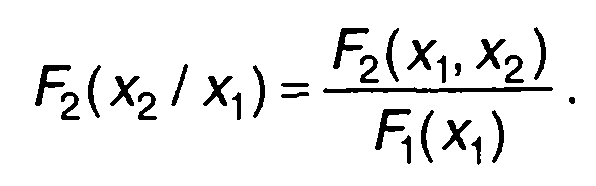(16.49)

Функция F₂(x₂/x₁) определяет вероятность того, что случайный процесс ξ(t) в момент времени t₂ не превышает уровень х₂ при ус­ловии, что в момент времени t₁ он не превышает уровень х₁ . Аналогично (16.49) определяются ФРВ n-го порядка.

С помощью условных ФРВ выражение для n-мерной ФРВ -

случайного процесса можно записать в виде

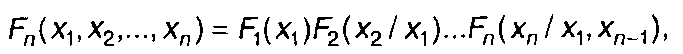(16.50)

где

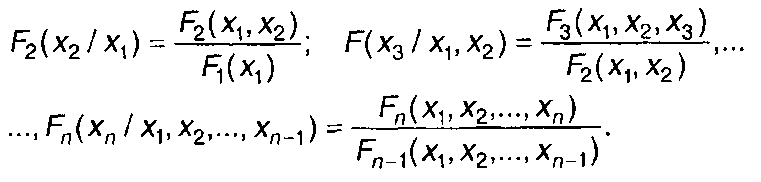(16.51)

Такое представление n-мерной ФРВ может оказаться полезным при её оценке с использованием ФРВ меньшей мерности.

Исходя из условных ФРВ можно определить и условные ПРВ случайного процесса. Условная ФРВ величены ξ(t₂), при условии, что значение величины ξ(t₁) лежит внутри интервала [x₁,x₁+∆x], определяется выражением

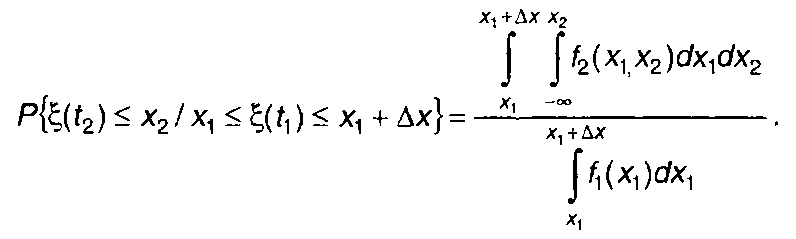(16.52)

Дифференцируя (16.52) по х₂ и переходя к пределу при ∆x→ 0, получим выражение для условной ПРВ случайного процесса

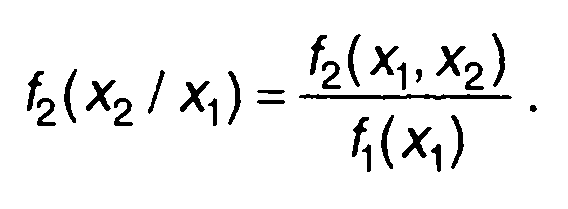(16.53)

Аналогично можно определить и другие условные ПРВ.

Если значение случайного процесса в момент времени t₂ не за­висит от того, какое значение принял случайный процесс в момент времени t₁ , то говорят о статистической независимости ξ(t₁) и ξ(t₂).

Для независимых случайных величин ξ(t₁)и ξ(t₂) выполняется ра­венство

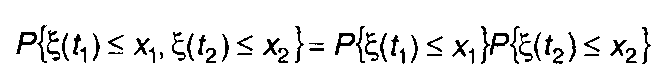(16.54)

или

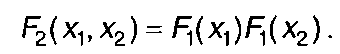(16.55)

л-мерная ФРВ независимых значений случайного процесса в мо­менты времени t₁, t₂, ..., t_n равна произведению л одномерных ФРВ

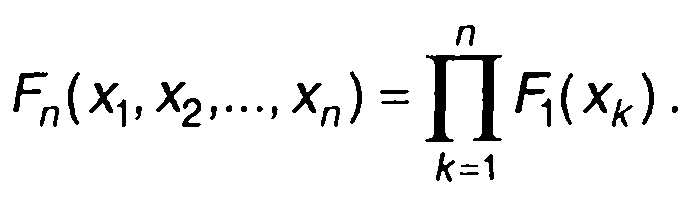(16.56)

Переходя к ПРВ такого случайного процесса, запишем

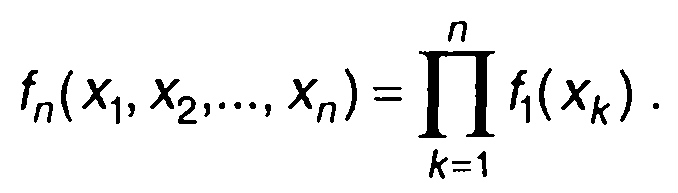(16.57)

Если равенства (16.56) или (16.57) выполняются для любых мо­ментов времени (t_k≠t₁), то случайный процесс полностью описы­вается одномерной ФРВ (ПРВ). Такой случайный процесс называ­ется совершенно случайным.

Условные ФРВ или ПРВ позволяют получить условные моменты распределения вероятностей. Так условное математическое ожи­дание случайного процесса в момент времени t₂ при заданном зна­чении случайного процесса в момент времени t₁ (ξ(t1) = x₁) опреде­ляется выражением

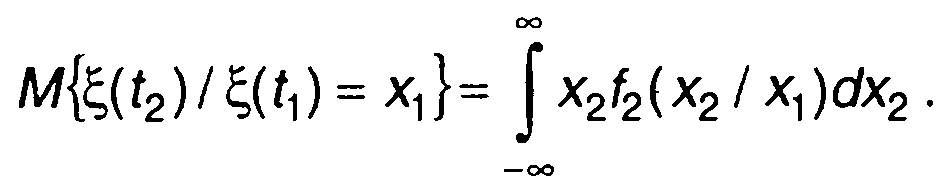(16.58)

В качестве примеров приведем условные характеристики рас­пределения гауссовского процесса. Для стационарного гауссовско­го процесса условную двумерную ПРВ получим из (16.49)

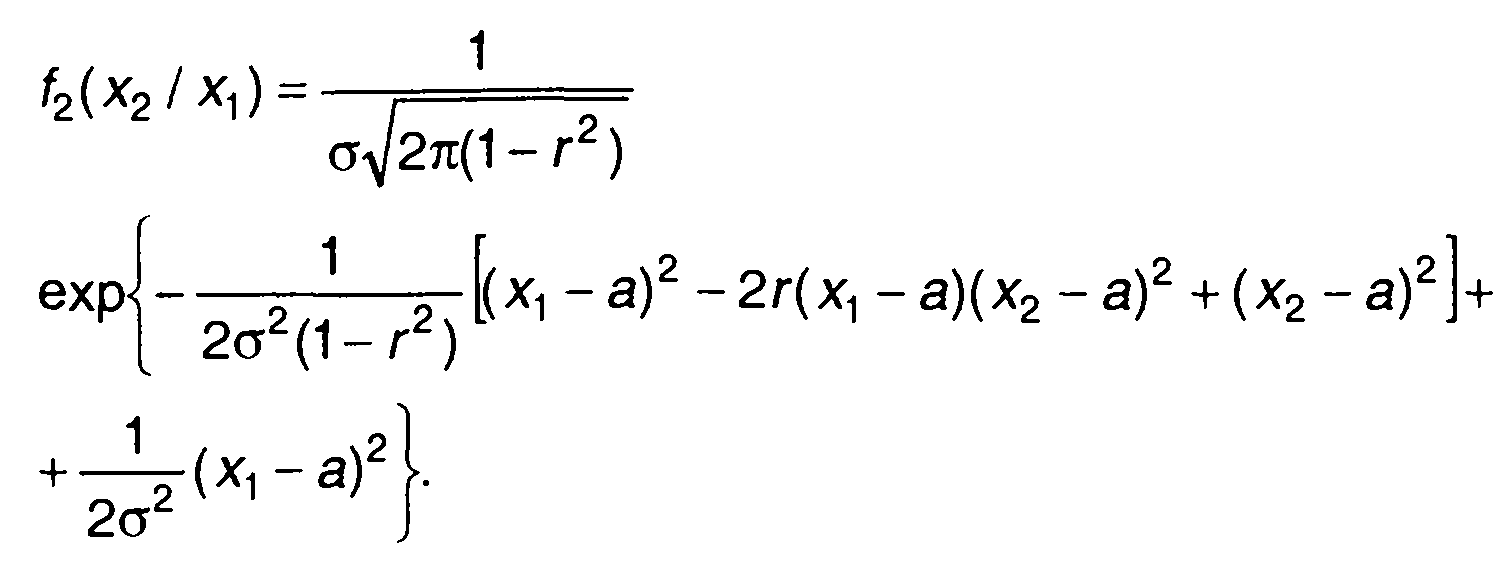(16.59)

Преобразовав (16.59), запишем

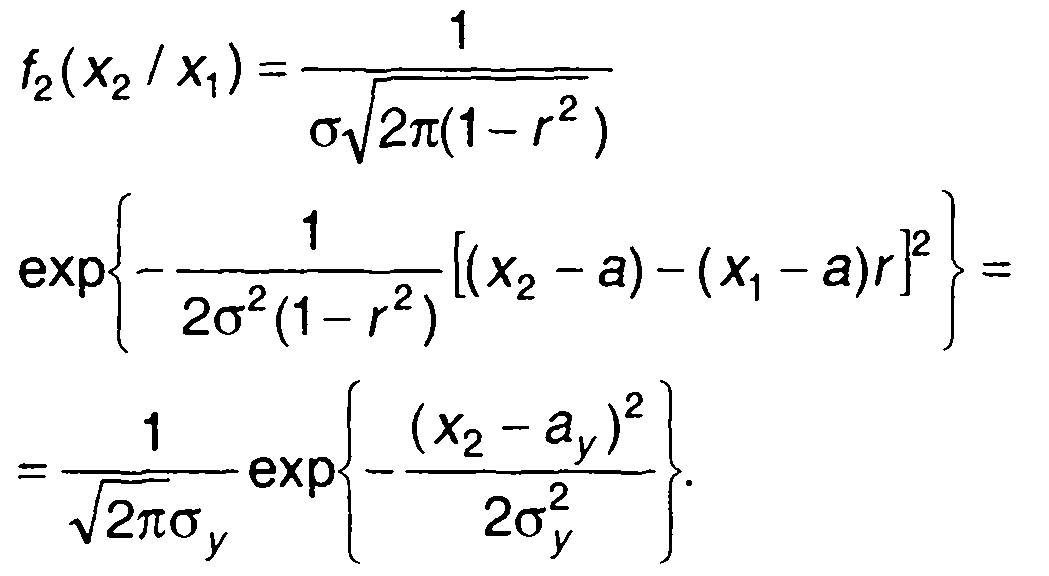(16.60)

Таким образом, условная ПРВ гауссовского процесса является нормальной; математическое ожидание равно а_у = rх₁ + а( 1 - r),

дисперсия σ_у² = σ²(1-r²). График условной ПРВ приведен на

рис. 16.7. (а = 0). При r=0 условная ПРВ переходит в одномерную ПРВ.

Условное математическое ожидание гауссовского процесса равно

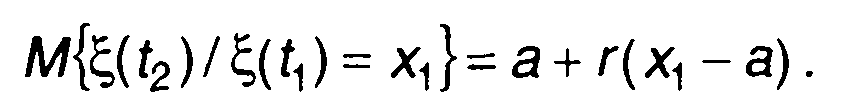(16.61)

Если r= 0, то условное математическое ожидание совпадает с безусловным.

Условная дисперсия определяется из (16.60) с учетом (16.61)

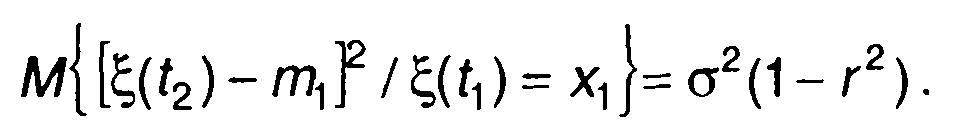(16.62)

Как следует из (16.62), дисперсия не зависит от значения ξ(t₁), а зависит только от корреляционной функции случайного процесса. При r = 0 условная дисперсия совпадает с дисперсией случайного процесса

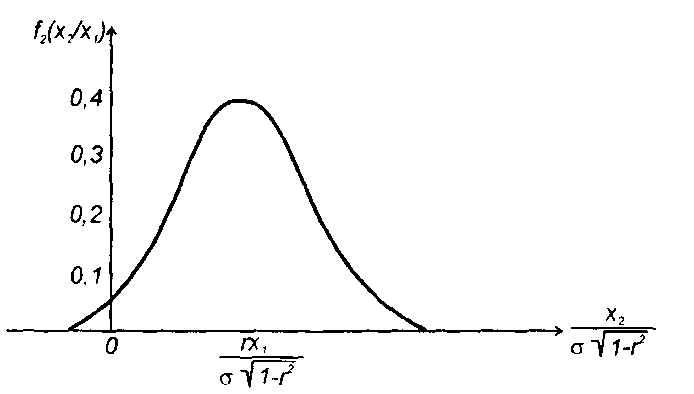
Рис. 16.7

16.6. Распределение случайного процесса на интервале времени

Одной из задач, решаемой при анализе случайного процесса, яв­ляется получение оценки ФРВ на заданном интервале времени - ве­роятности того, что случайный процесс внутри заданного интервала времени Г не превысит установленного уровня х (рис. 16.2). Такой оценкой может служить (n + 1)-мерная ФРВ случайного процесса

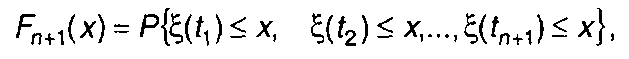(16.63)

где t₁, t₂, t_n+1 - точки разбиения интервала

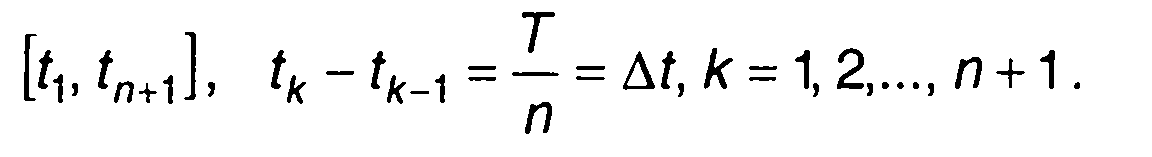
ФРВ (n + 1)-гo порядка представим с помощью условных ФРВ

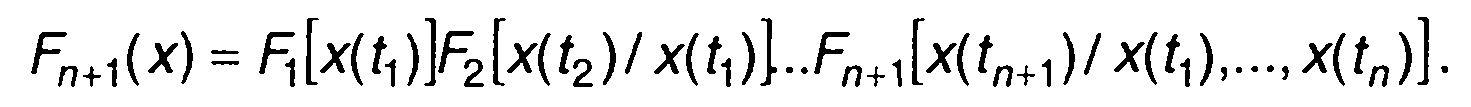(16.64)

Условные ФРВ в (16.64) можем приближенно вычислить с помощью ФРВ меньших порядков. При этом учтем следующее неравенство:

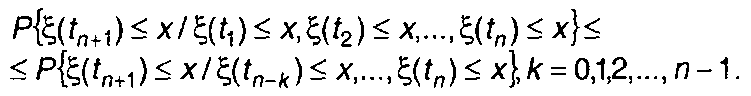(16.65)

Ограничиваясь в (16.64) ФРВ мерности не выше второй, полу­чим оценку ФРВ (n+1 )-го порядка в виде

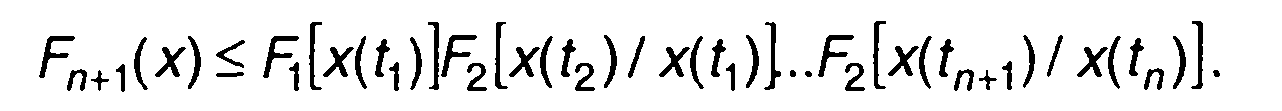(16.66)

Для стационарного случайного процесса выражение (16.66) мо­жет быть записано как

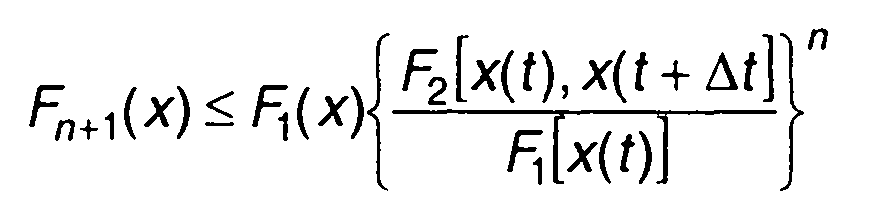(16.67)

или

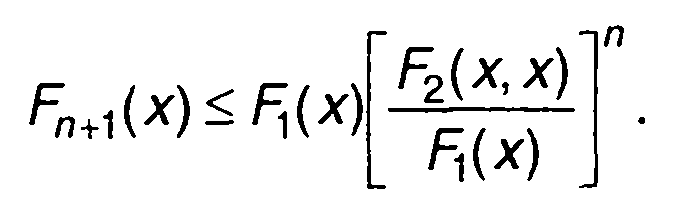(16.68)

Неравенство (16.68) дает оценку сверху (n+1)-мерной ФРВ ста­ционарного случайного процесса с помощью двумерной ФРВ. Оценка может быть уточнена при использовании ФРВ третьего, четвертого и т. д. порядков.

Конкретизируем выражение (16.68) для гауссовского процесса. С целью упрощения записи будем рассматривать центрированный случайный процесс с σ = 1

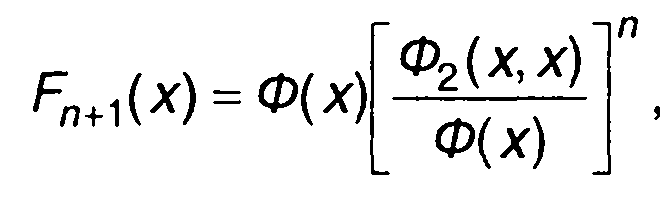(16.69)

где Ф(х), Ф₂ (х, х) - табулированные функции, описываемые (15.27) и (16.23).

При достаточно малом значении ∆t двумерную ФРВ можно раз­ложить в ряд Тейлора. Ограничиваясь в ряде Тейлора (16.31) пер­выми двумя членами, запишем

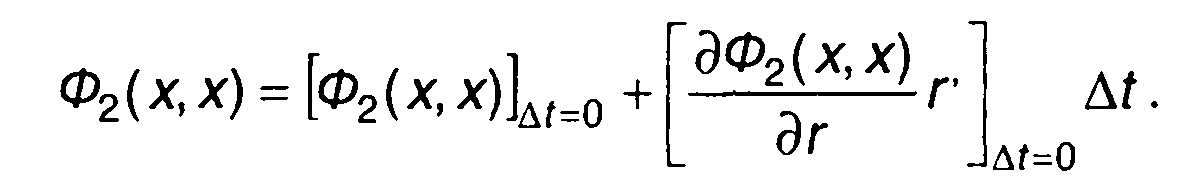(16.70)

Учитывая (16.29), выражение (16.70) получаем в виде

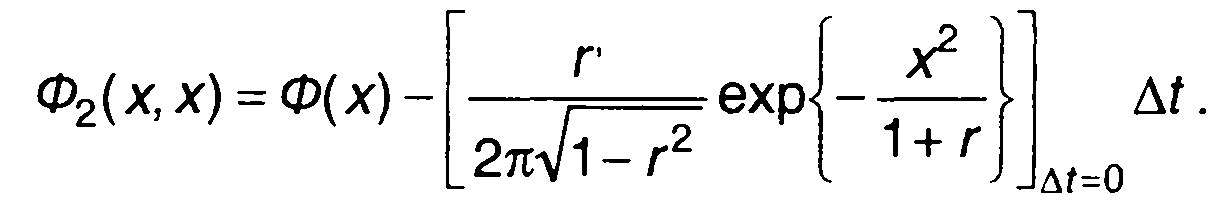(16.71)

Рассмотрим следующее предельное соотношение

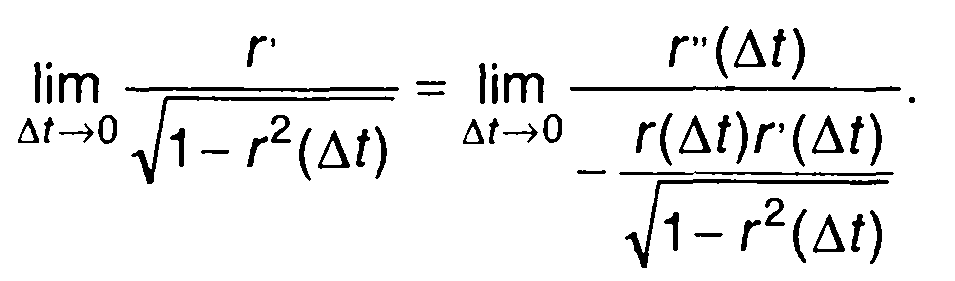
Для него получим

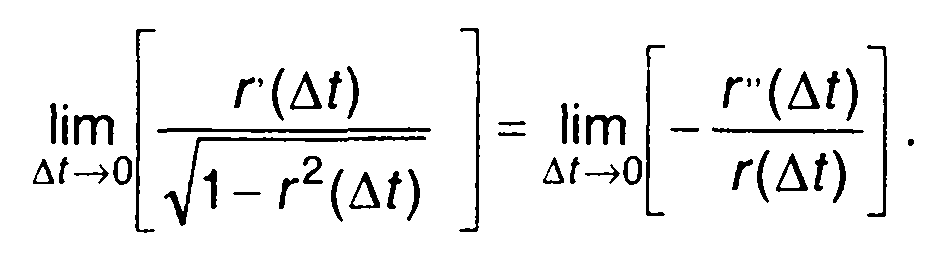
Таким образом, имеем

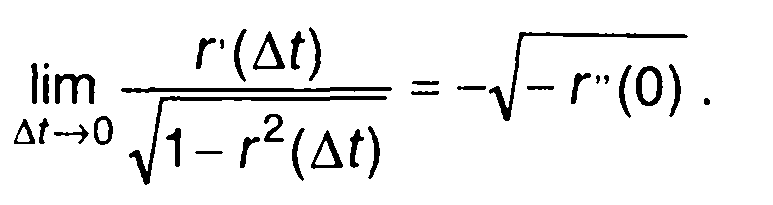(16.72)

С учетом (16.72) выражение (16.71) запишем в виде

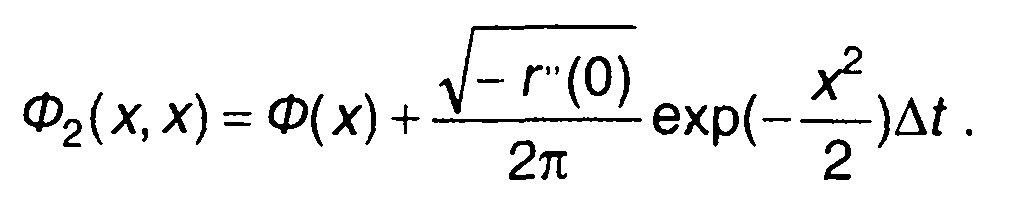(16.73)

Подставив (16.73) в (16.69), получим

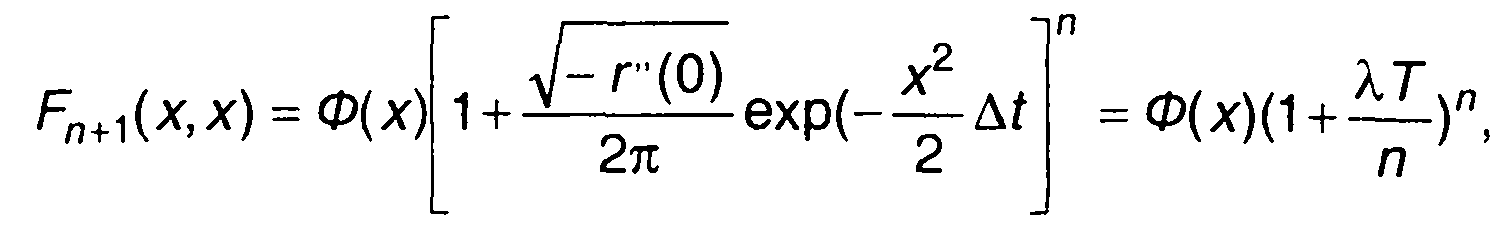(16.74)

где

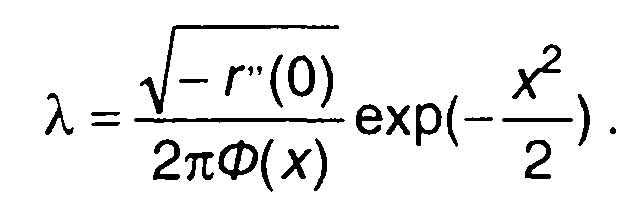(16.75)

Переходя к пределу при n→∞, уточним оценку распределения случайного процесса на интервале Т

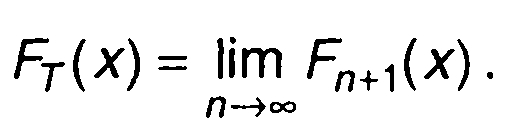(16.76)

Из (16.74) получим

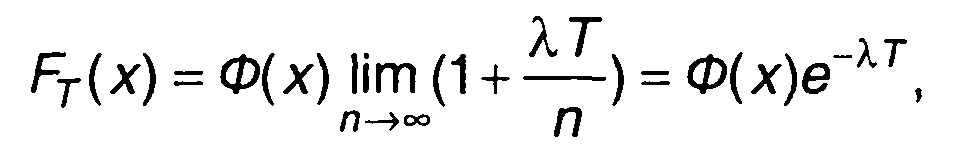(16.77)

где

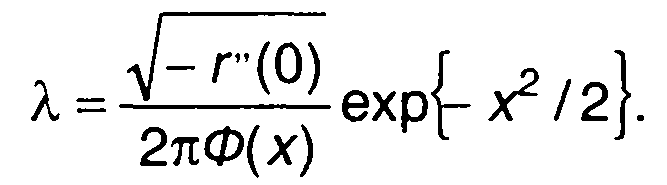
В общем виде выражение для ФРВ гауссовского процесса на ин­тервале времени Т (её оценки) представим как

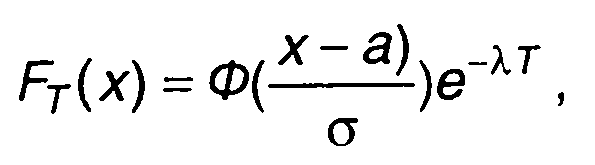(16.78)

где

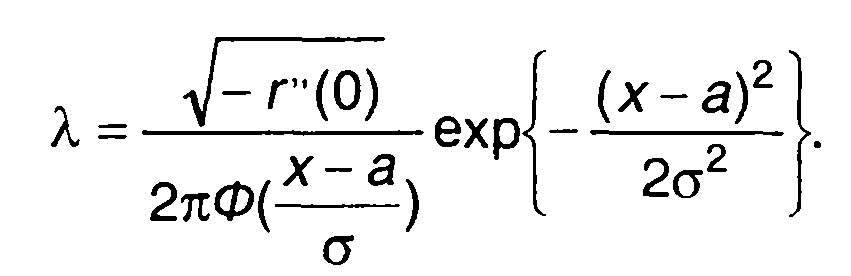(16.79)

Здесь а, σ, r(т) - математическое ожидание, дисперсия и нормиро­ванная корреляционная функция случайного процесса.

При T=0 случайный процесс рассматривается для одного мо­мента времени; из (16.78) следует

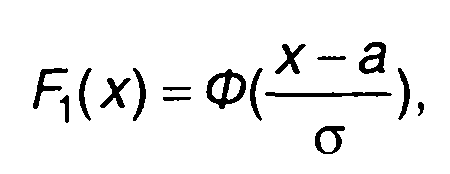(16.80)

что соответствует ожидаемому результату. Чем больше интервал времени T, тем меньше F_T(x), что также очевидно. Уменьшение

F_T(x)при увеличении Т описывается экспоненциальной зависи­мостью (с отрицательным показателем степени). Графики F_T(x) в зависимости от Т(λТ) представлены на рис. 16.8.

16.7. Многомерная характеристическая функция случайного процесса

Понятие характеристической функции, введенное для одной случайной величены, может быть распространено на совокупность случайных величин: ξ(t₁),ξ(t₂),...,ξ(t_n) - значений случайного про­цесса в различные моменты времени, n-мерная характеристиче­ская функция случайного процесса определяется как среднее зна­чение функции

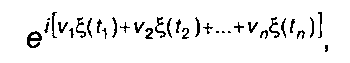
где v₁,v₂,.-.,v_n — действительные величины.

Таким образом, n-мерная характеристическая функция случай­ного процесса определяется выражением

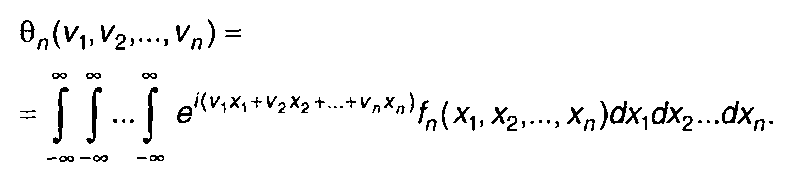(16.81)

Как следует из (16.81), n-мерная характеристическая функция представляет n-кратное обратное преобразование Фурье n-мерной ПРВ случайного процесса (без учета коэффициента). Прямое пре­образование Фурье позволяет перейти от характеристической функции к ПРВ случайного процесса

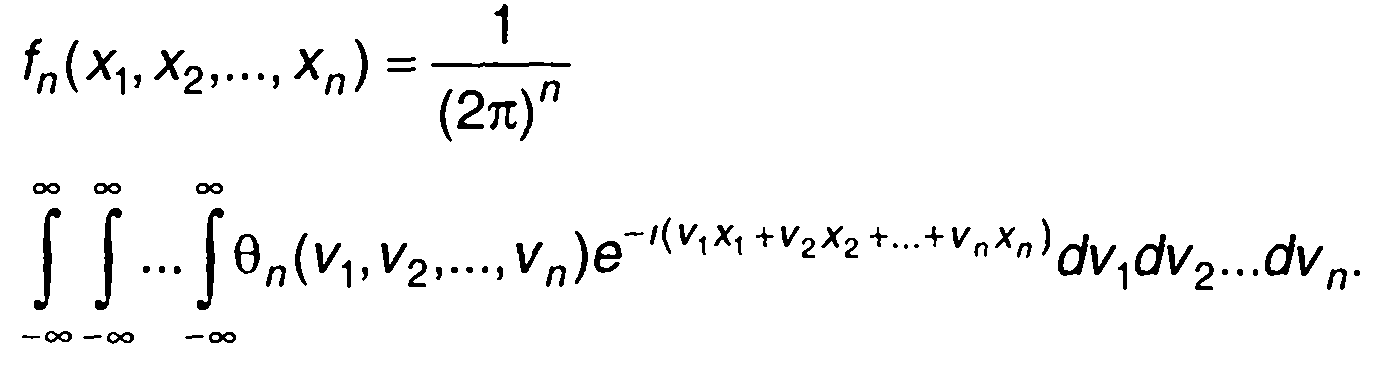(16.82)

Из характеристической функции n-го порядка можно получить характеристические функции меньших порядков

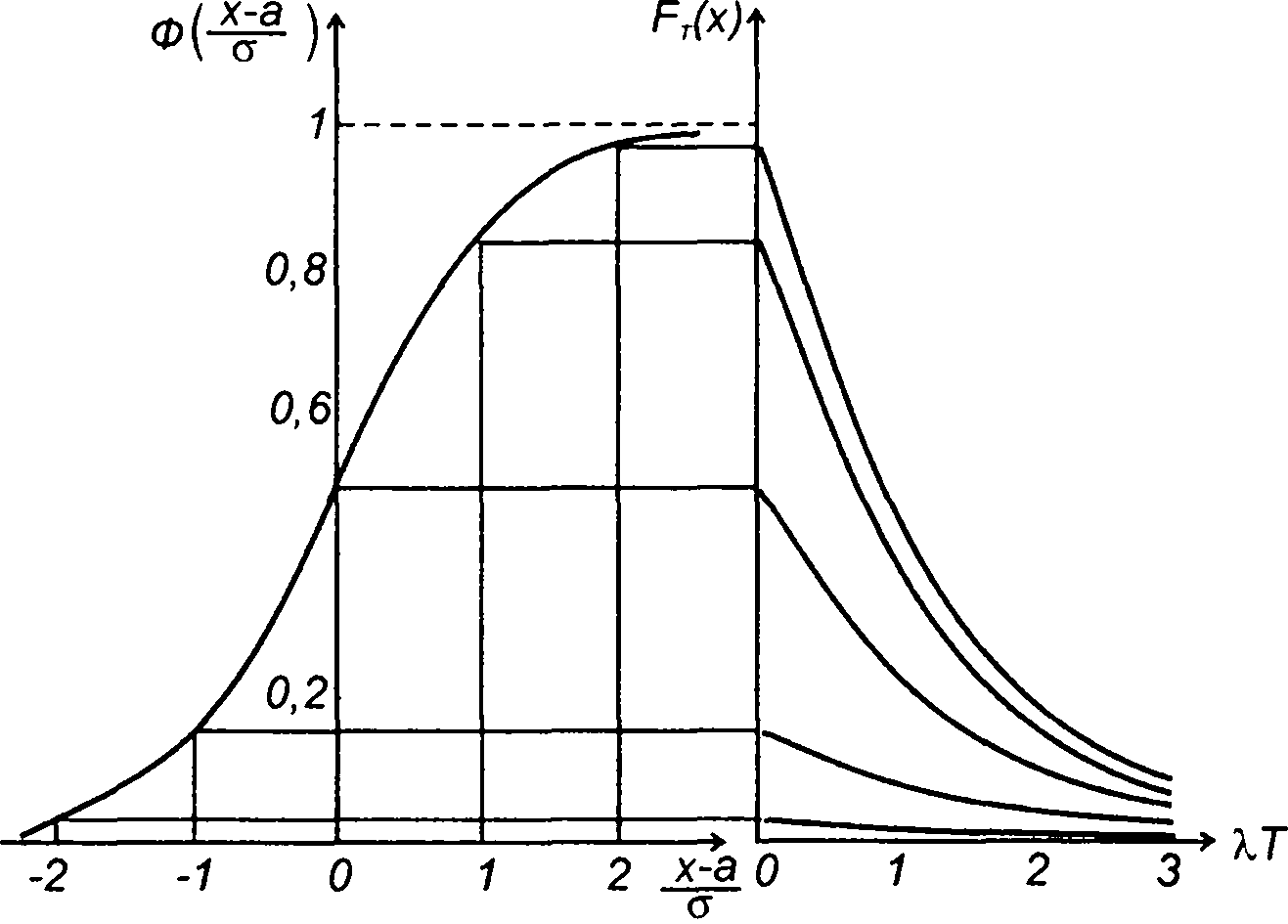
Рис. 16.8

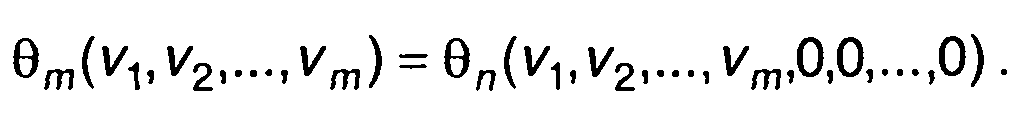(16.83)

Характеристическая n-мерная функция позволяет определить моменты распределения вероятностей случайного процесса. Про­изводная n-го порядка характеристической функции определяется выражением

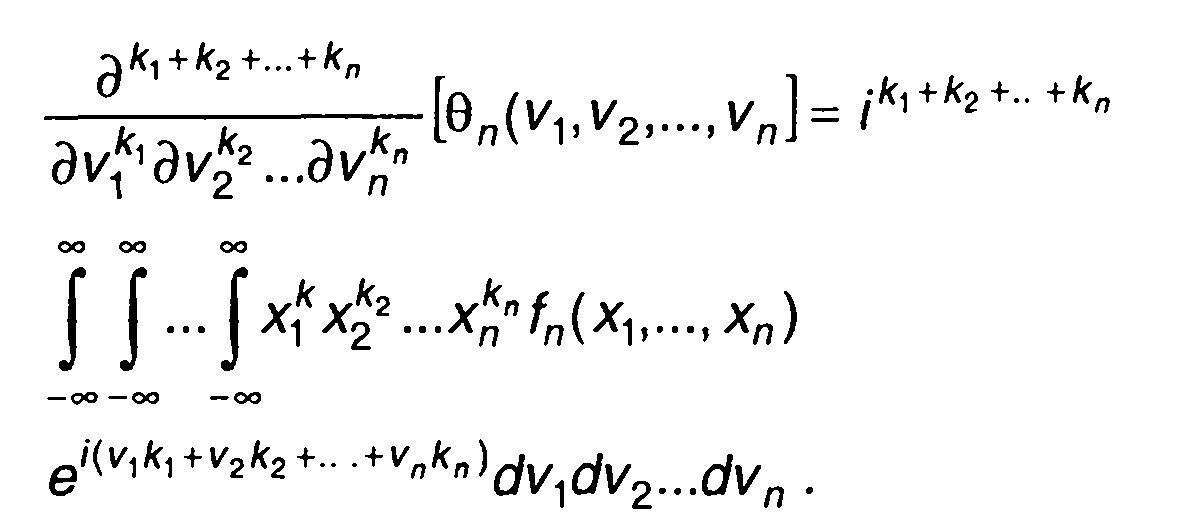(16.84)

Из (16.84) получим выражение для начальных моментов рас­пределения вероятностей случайного процесса

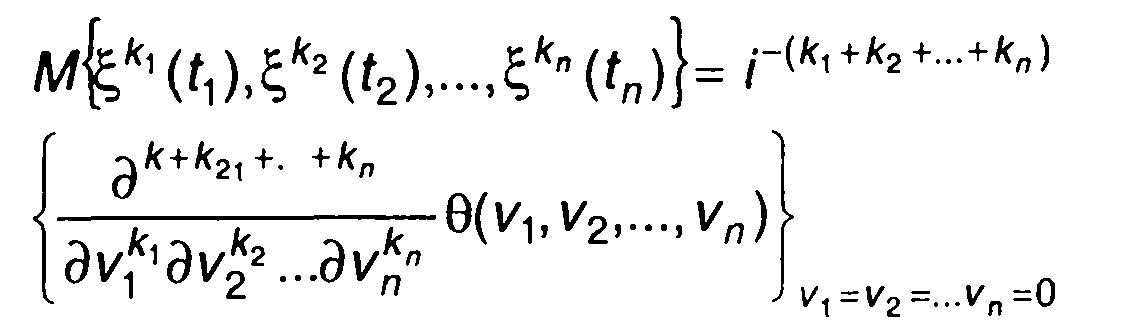(16.85)

Таким образом, имея характеристическую функцию, можно

определить ПРВ и начальные моменты распределения вероятностей случайного процесса.

Если случайные величины независимы, то математическое ожи­дание их произведения равно произведению математических ожи­даний каждой из них. Исходя из этого, для независимых случайных величин ξ(t₁), ξ(t₂), ...,ξ(t_n), можем записать

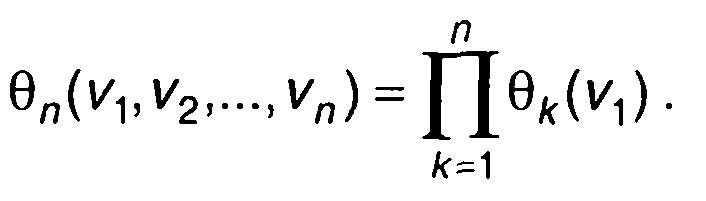(16.86)

Справедливо и обратное утверждение: если n-мерная характери­стическая функция равна произведению одномерных характеристи­ческих функций, то случайные величины являются независимыми.

Для гауссовского процесса выражение для n-мерной характери­стической функции получим с учетом (16.36) в виде

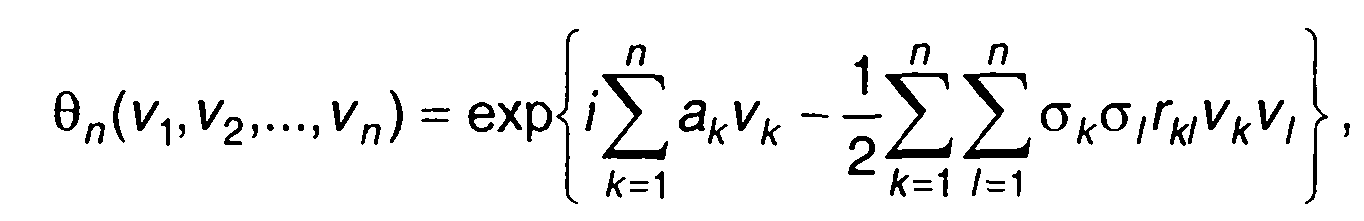(16.87)

где а_к, σ²_к, r_kl - математическое ожидание, дисперсия и нормиро­ванная корреляционная функция случайного процесса.

При n = 2 получим выражение для двумерной характеристиче­ской функции стационарного гауссовского процесса

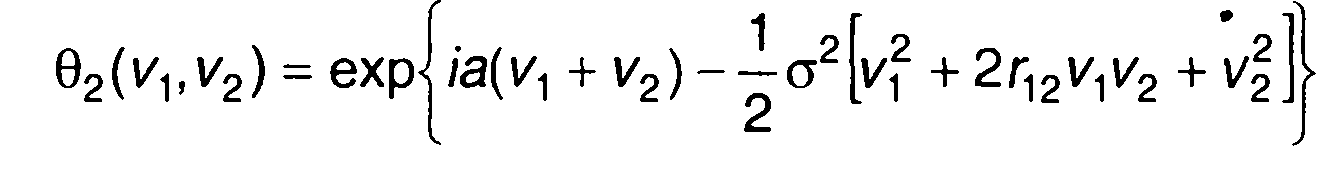(16.88)

16.8. Марковские процессы

Одной из полезных для практики исследования моделей случай­ных процессов является процесс Маркова или случайный процесс без последствия. Марковским процессом называют такой случай­ный процесс, для которого условную ПРВ можно записать в виде