ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 14 страница
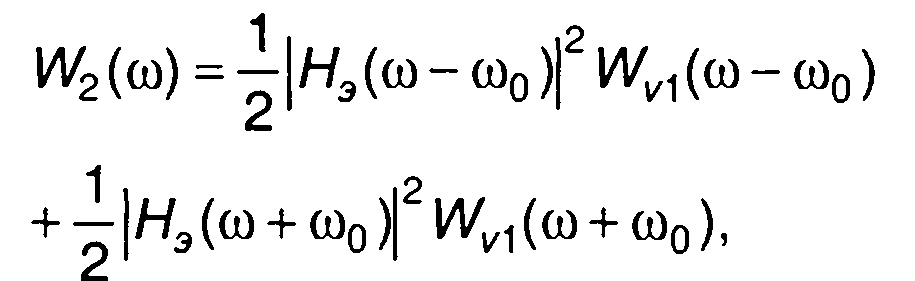(13.48)
где Wv1(ω) — спектральная плотность энергии комплексной огибающей сигнала на входе цепи.
Переходя к временной области, для комплексной огибающей сигнала на выходе цепи запишем
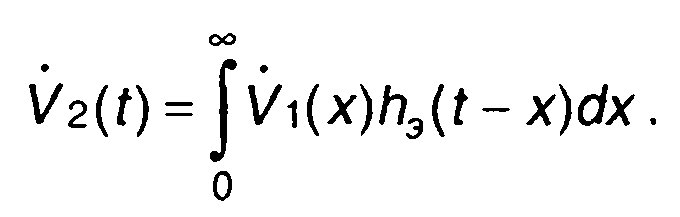(13.49)
Сигнал на выходе узкополосной цепи описывается выражением
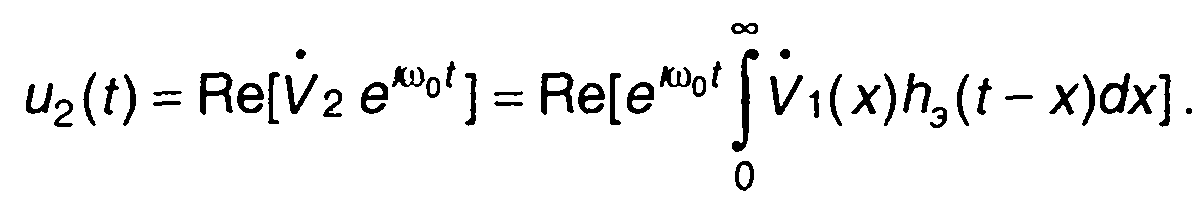(13.50)
Таким образом, записаны выражения, описывающие сигнал на выходе узкополосной цепи при подаче на ее вход узкополосного сигнала.
В качестве примера рассмотрим прохождение экспоненциального радиоимпульса
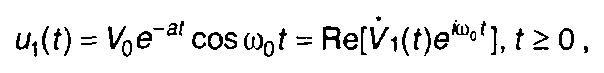
где V1(t) = V0e-at - огибающая сигнала, через LCR-цепь (рис. 13.4).
Импульсная характеристика эквивалентной низкочастотной цепи имеет вид
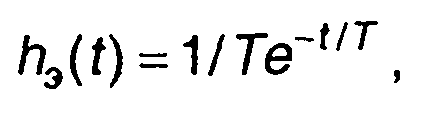
где T=2L/R.
Для огибающей сигнала на выходе цепи запишем
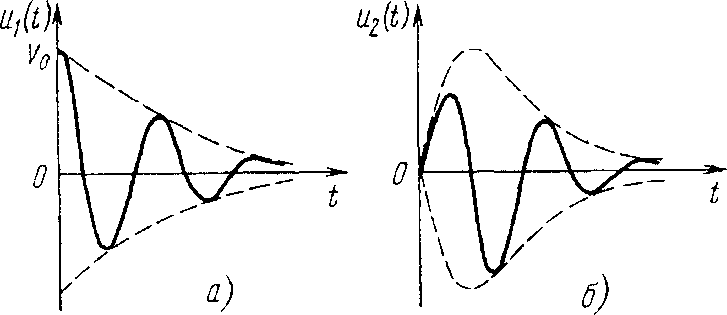
Рис. 13.5
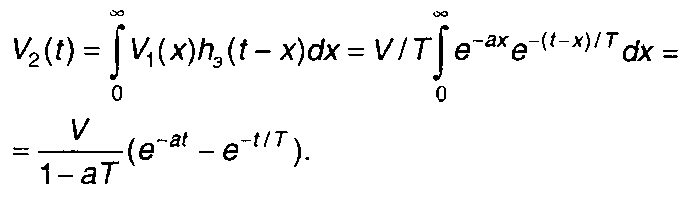
Сигнал на выходе цепи описывается выражением (рис. 13.5)
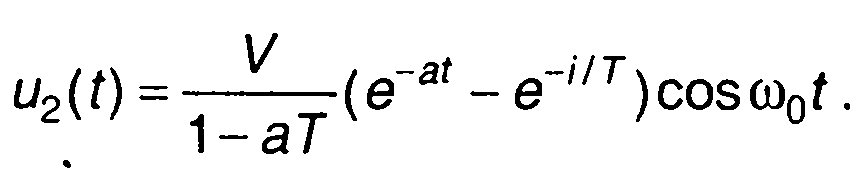
13.3. Прохождение сигнала через цифровой фильтр
При анализе дискретных сигналов и при описании цифровой обработки сигналов наиболее широкое применение нашло z-преобразование. Линейная цепь в цифровом выполнении (соответствующая программа ЭВМ) называется цифровым фильтром. Одной из основных характеристик цифрового фильтра (как и аналоговой линейной цепи) является импульсная характеристика. Она представляет отклик цифрового фильтра на воздействие единичного импульса. Используя импульсную характеристику фильтра, для каждого входного сигнала можно определить сигнал на выходе. Сигнал на выходе описывается дискретной сверткой импульсной характеристики h(kT) и сигнала на входе s1(kT)
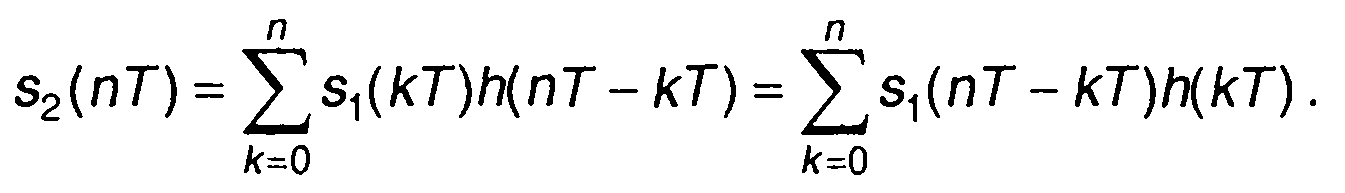(13.51)
Записанное выражение представляет алгоритм цифровой фильтрации во временной области. Графическое отображение алгоритма дано на рис. 13.6.
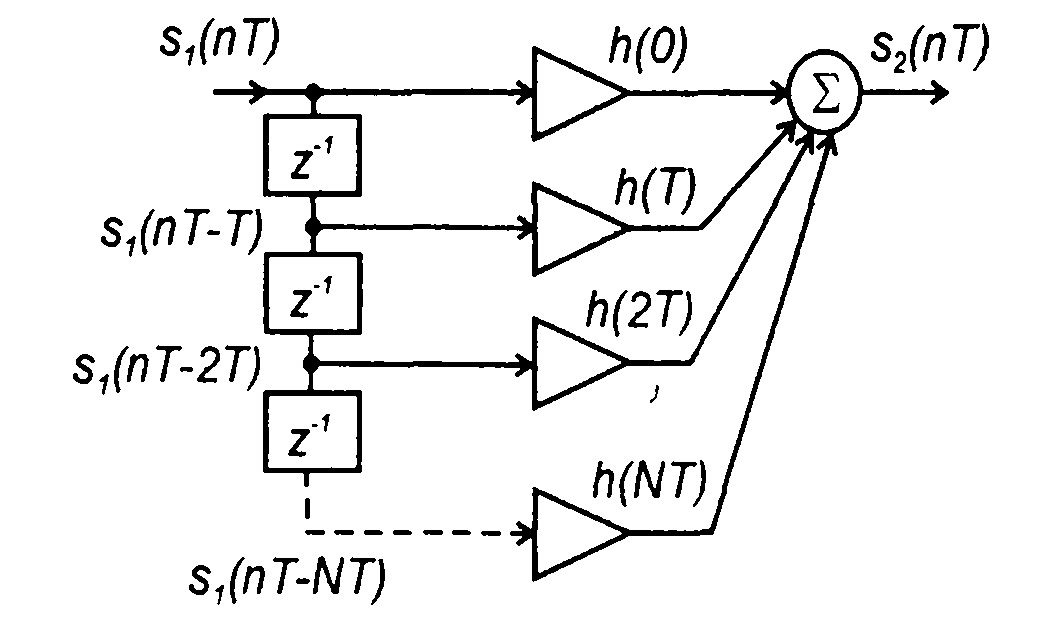
Рис.13.6
ход - с использованием z-преобразования позволяет упростить анализ прохождения сигналов через цифровые фильтры.
Одним из методов анализа прохождения сигналов через аналоговые цепи является метод составления и решения дифференциальных уравнений.
Примером такого уравнения является уравнение, описывающее прохождение сигнала через RС-цепь
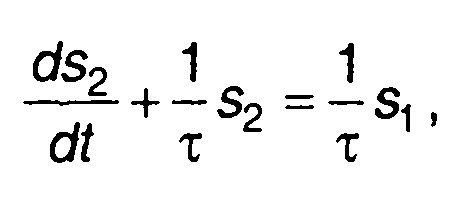
где s1, s2- сигналы на входе и выходе цепи;
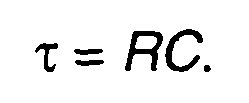
Для дискретных сигналов дифференциальному уравнению 1-го порядка соответствует разностное уравнение
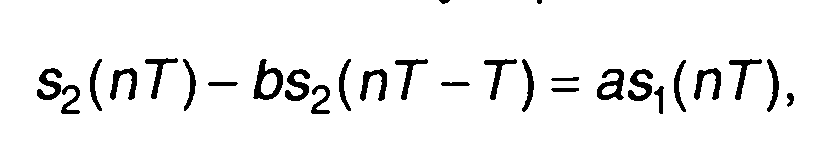(13.54)
где T - интервал дискретизации.
Преобразуя уравнение (13.54), запишем
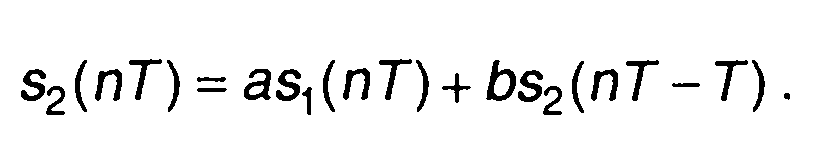(13.55)
Как следует из (13.55), в цифровом фильтре значение выходного сигнала может использоваться при расчетах последующих значений. Такие фильтры называются рекурсивными.
В общем случае разностное уравнение N-го порядка имеет вид
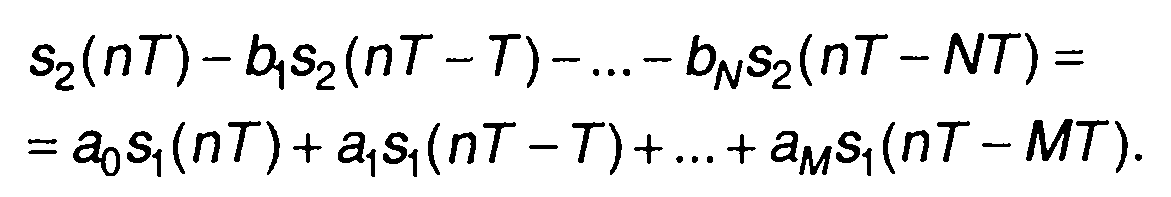(13.56)
Перепишем его в виде
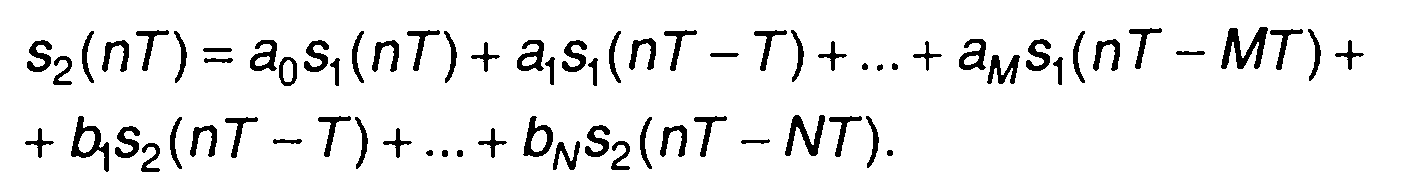(13.57)
Схема рекурсивного фильтра, реализующая алгоритм (13.57), представлена на рис. 13.7.
Системная функция такого фильтра найдется, если в (13.56) перейти к z-преобразованию левой и правой частей
На рис. 13. 6 элемент задержки обозначен в терминах z-преобразования как z-1 (свойство z-преобразования). Схема показывает последовательность вычислительных операций. При расчете значений выходного сигнала используются только значения входного сигнала. Фильтры, в которых для расчета выходного сигнала используются только значения входного сигнала (отсутствует обратная связь), называются простыми или нерекурсивными. Для практической реализации таких фильтров необходимо, чтобы импульсная характеристика содержала конечное число членов (или можно было бы ограничиться конечным числом членов).
При анализе цифровых фильтров наряду с импульсной характеристикой используется системная функция. Она играет такую же роль, как частотная характеристика при анализе аналоговых цепей. Системная функция определяется как z-преобразование импульсной характеристики цифрового фильтра
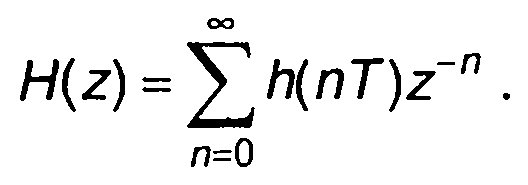(13.52)
Системная функция описывает свойства цифрового фильтра в области переменного z.
В качестве примера рассмотрим цифровой фильтр, соответствующий аналоговой RС-цепи. Импульсная характеристика фильтра имеет вид
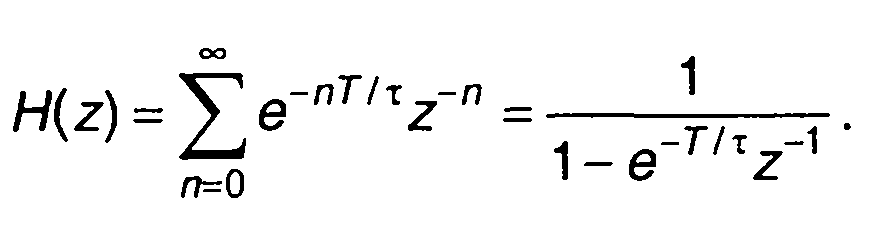
где т - постоянная времени. Ей соответствует системная функция
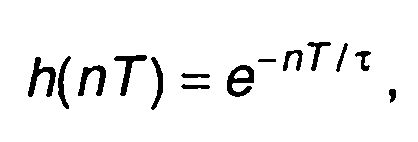
Z-преобразование дискретной свертки (13.51) дает следующее равенство (свойство z-преобразования)
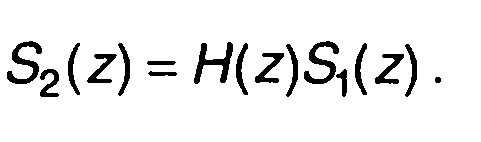(13.53)
Таким образом, z-преобразование сигнала на выходе цифрового фильтра равно произведению системной функции фильтра и z- преобразования сигнала на входе. Обратное z-преобразование позволяет перейти к сигналу на выходе фильтра. Часто такой
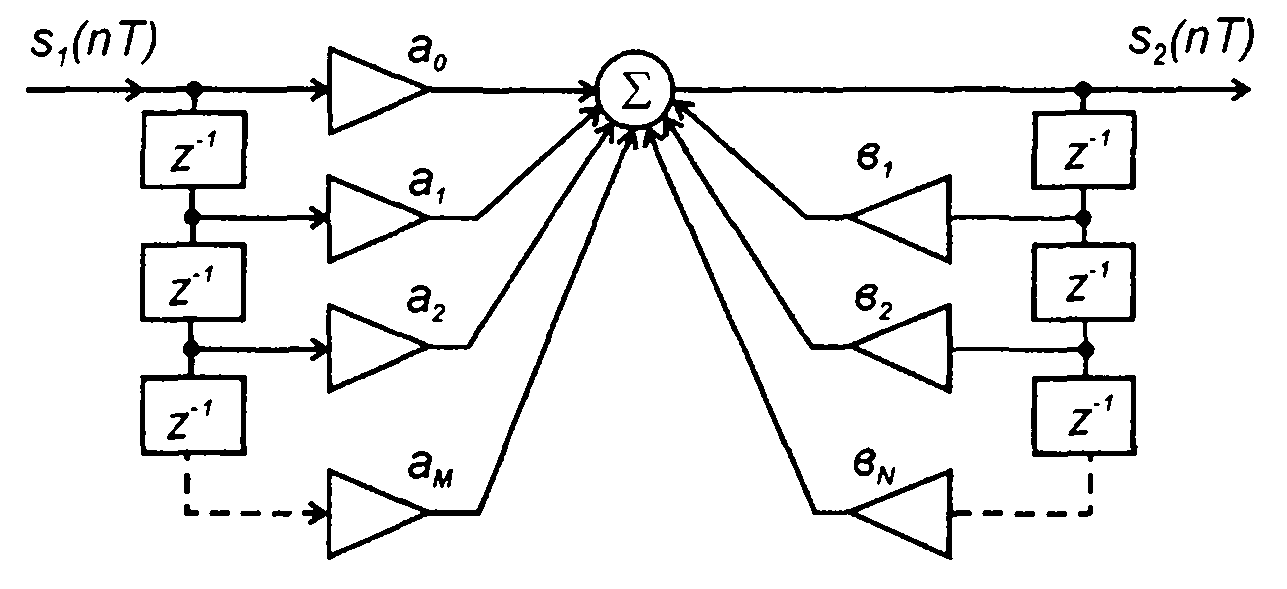
Рис. 13.7
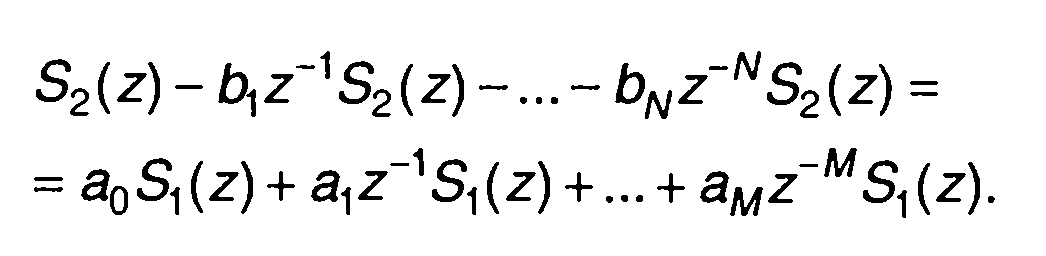(13.58)
Таким образом, получим
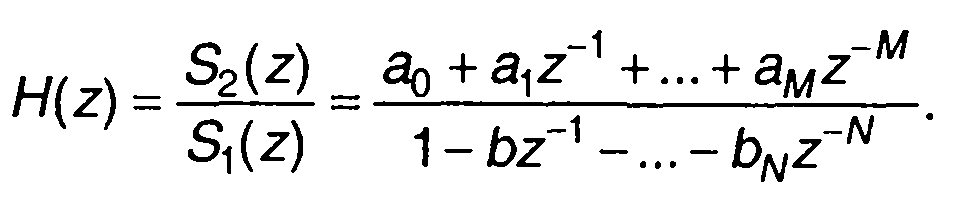(13.59)
Анализ (13.59) показывает, что коэффициенты слагаемых числителя определяют нерекурсивную часть фильтра, а коэффициенты слагаемых знаменателя определяют рекурсивную часть фильтра.
В качестве примера рассмотрим цифровой фильтр, соответствующий аналоговой цепи с импульсной характеристикой (колебательный контур)
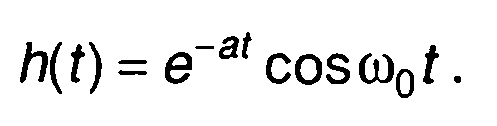
Импульсная характеристика цифрового фильтра имеет вид
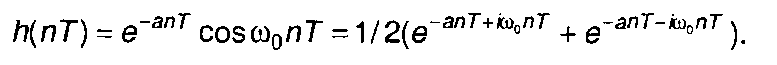
Системная функции, соответствующая h(nT), может быть найдена как.
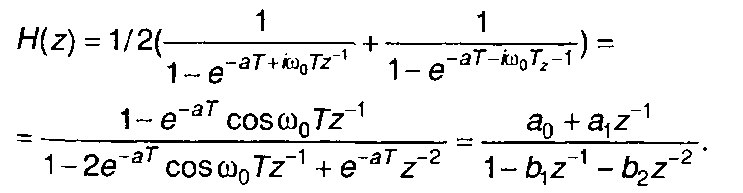
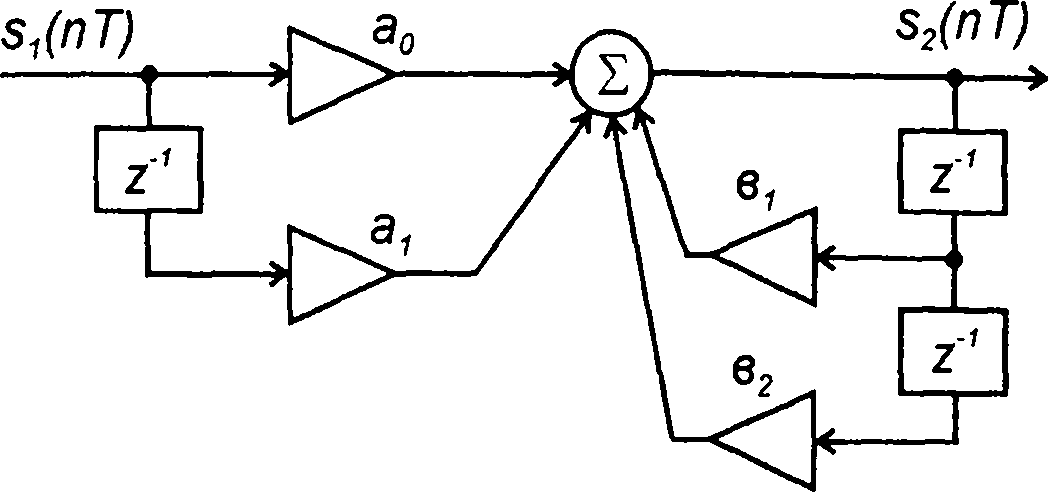
Рис. 13.8
Системной функции соответствует уравнение
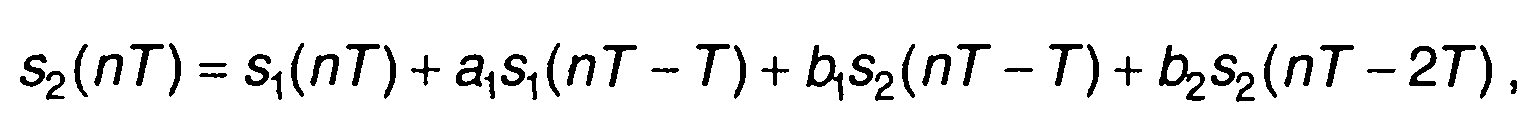
где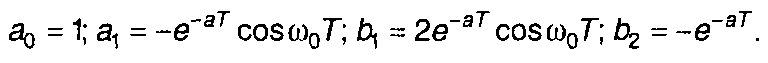 
Схема цифрового фильтра, отражающая полученный алгоритм, приведена рис. 13.8.
Фильтр, схема которого приведена на рис. 13.7, может быть реализован несколько иначе. Запишем (13.59) в виде
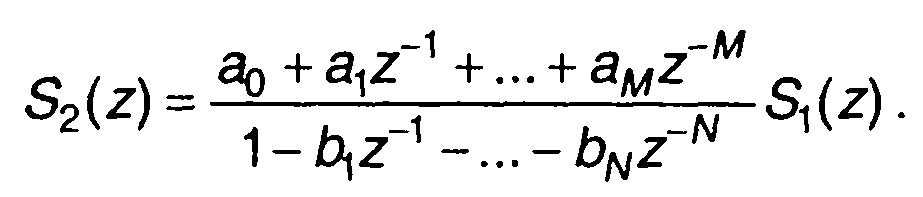(13.60)
Представим (13.60) как
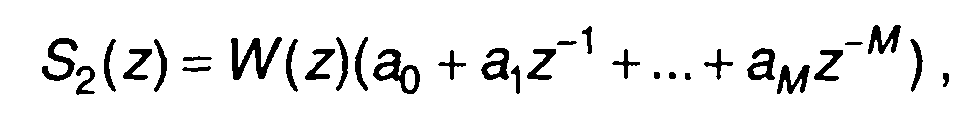(13.61)
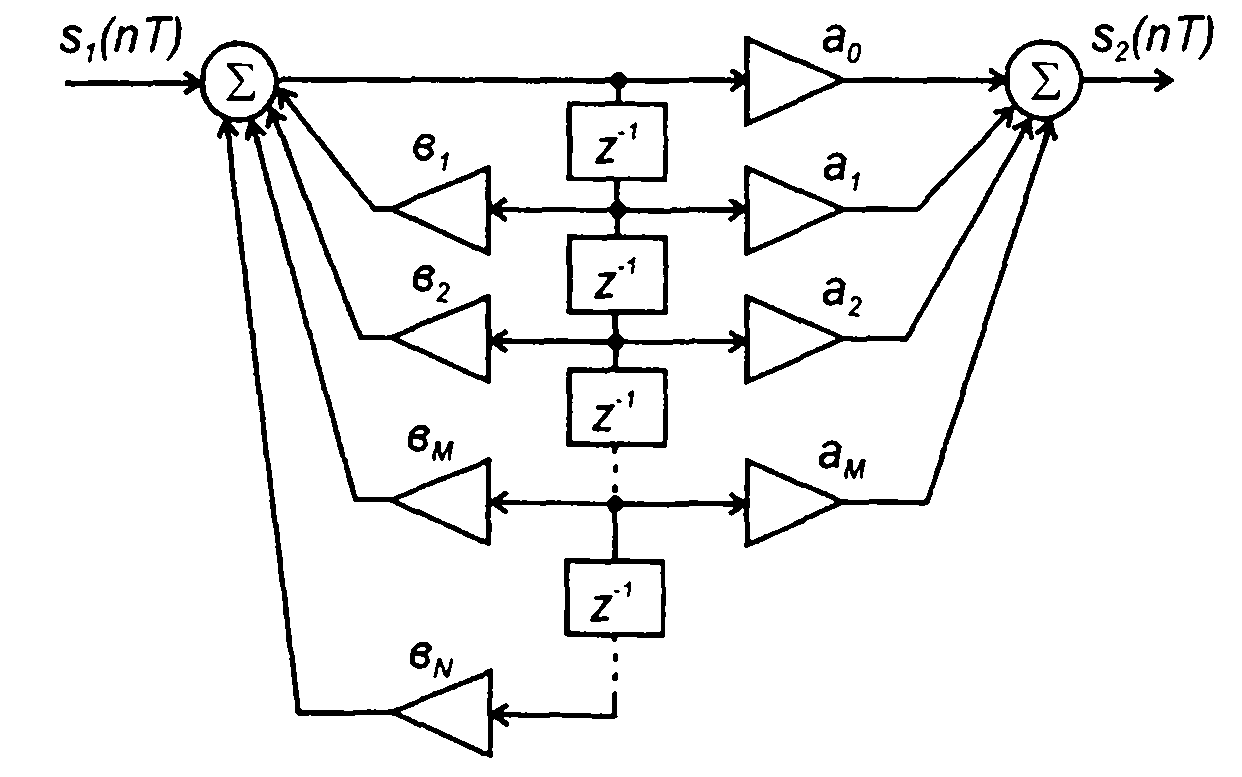
Рис. 13.9
где
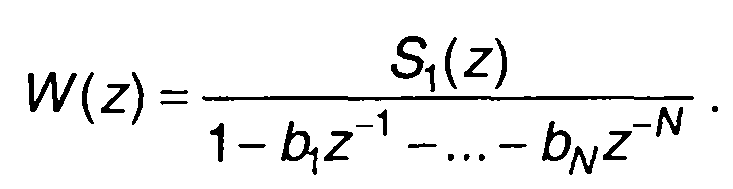(13.62)
Преобразование, соответствующее W(z), осуществляется с помощью рекурсивного фильтра N-го порядка. Выражению (13.61) соответствует нерекурсивное преобразование сигнала. Таким образом, может быть изображена общая схема цифрового фильтра, включающая нерекурсивную и рекурсивную части. Дублирующие элементы схемы (элементы задержки) объединены (рис. 13.9). Такая схема фильтра называется канонической.
Приведенные примеры иллюстрируют практику применения z-преобразования, его полезность при анализе дискретных сигналов.
СПИСОК ЛИТЕРАТУРЫ К ЧАСТИ 1
1. Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. -М.: Наука, 1965.
2. Баскаков С.И. Радиотехнические цепи и сигналы. -М.: Высшая школа, 1988.
3. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. -М. : Наука, 1966.
4. Бендат Дж., Пирсол А. Применения корреляционного анализа. - М.: Мир, 1983.
5. Бокс Дж., Дженкинс Г. Анализ временных рядов. Вып.1 и вып.2. - М.: Мир, 1974.
6. БрейсуДанилэлл Р. Преобразование Хартли. -М.: Мир, 1990.
7. Варакин Л.Е. Системы связи с шумоподобными сигналами. -М.: Радио и связь, 1985
8. Варакин Л.Е. Теория сложных сигналов. -М.: Сов. радио, 1970.
9. Гиллемин Э. А. Синтез пассивных цепей. -М.: Связь, 1970.
10. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. -М.: Радио и связь, 1985.
11. Гоноровский И. С. Радиотехнические цепи и сигналы. -М.: Радио и связь, 1986.
12. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. -М.: Госиздат физико-математической литературы, 1963.
13. Данилов В.Л. и др. Математический анализ. -М .: Изд. Физ. мат. литературы, 1961.
14. Денисенко А.Н., Стеценко О.А. Теоретическая радиотехника. Сигналы. -М.: Изд. Стандартов, 1993.
15. Денисенко А.Н. Сигналы с фазовой и частотной модуляцией. -М.: Изд. Стандартов, -1994.
16. Диксон Р.К. Широкополосные системы. -М.: Связь, 1979.
17. Диткин В.А., Прудников А П. Интегральные преобразования и операционное исчисление. -М.: Изд. Физ. мат. литературы, 1961.
18. Каганов В.И. Радиотехника, компьютер, mathcad. -М.: Горячая линия-телеком, 2001.
19. Карташов В.Г. Основы теории дискретных сигналов и цифровых фильтров. -М.: Высшая школа, 1982.
20. Картьяну Г. Частотная модуляция. -М.: Изд. АРНР, 1961.
21. К.Де.Бор. Практическое руководство по сплайнам. -М.: Радио и связь, 1985.
22. Кузнецов Д.С. Специальные функции. -М.: Высшая школа, 1965.
23. Кук Ч., Бернфельд М. Радиолокационные сигналы. -М.: Сов. радио, -1974.
24. Лезин Ю.С. Оптимальные фильтры и накопители импульсных сигналов. -М.: Сов. Радио, 1963.
25. Лэм Г. Аналоговые и цифровые фильтры. -М.: Мир, 1982.
26. Люк Ю. Специальные математические функции и их аппроксимации. -М.: Мир, 1980.
27. Люстерник Л.А. и др. Математический анализ. -М.: Изд. Физ. мат. литературы, 1963.
28. Макаров И.М., Менский Б.М. Линейные автоматические системы. - М.: Машиностроение, 1982.
29. Пестряков В.Б., Афанасьев В.П. и др. Шумоподобные сигналы в системах передачи информации. -М.: Сов. радио, 1973.
30. Петрович Н.Т., Размахнин М.К. Системы связи с шумоподобными сигналами. -М.: Сов. радио, 1989.
31. Пышкин И.М., Дежурный И.И. и др. Системы подвижной радиосвязи. -М.: Радио и связь, 1986.
32. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. -М.: Мир, 1978.
33. Свистов В.М. Радиолокационные сигналы и их обработка. -М.: Сов . радио, 1977.
34. СибертУ.М. Цепи, сигналы, системы, ч.1 и ч.2. -М.: Мир, 1982.
35. Современная радиолокация. -М.: Сов. Радио, 1969.
36. Стейн С., Джонс Дж. Принципы современной теории связи и их применение к передаче дискретных сообщений. -М.: Связь, 1971.
37. Справочник по специальным функциям. Под ред. М. Абрамовица и И. Стиган. -М.: Наука, 1979.
38. Сухорученков Б.И. Математические модели и методы анализа характеристик летательных аппаратов. -М.: Изд.МО, 1989.
39. Трахтман А.М. Введение в обобщенную спектральную теорию сигналов. -М.: Сов. радио, 1972.
40. Тузов Г.И. Статистическая теория приема сложных сигналов. -М.: Сов. радио, 1977.
41. Тузов Г.И., Сивов В.А. и др. Помехозащищенность радиосистем со сложными сигналами. -М.: Радио и связь, 1985.
42. Шумоподобные сигналы в системах передачи информации. Под ред. Пестрякова В.Б. -М.: Сов. радио, 1973.
43. Френке Л. Теория сигналов. -М.: Сов. радио, 1974.
44. Хармут Х.Ф. Передача информации ортогональными функциями. - М.: Связь, 1975.
45. Хармут X. Теория секвентного анализа. Основы и применения. -М.: Мир, 1980.
46. Хеминг Р.В. Цифровые фильтры. -М.: Сов. радио, 1980.
47 Янке Е., Эмде Ф., Леш Ф. Специальные функции. -М.: Наука, 1988.
ЧАСТЬ 2.
СЛУЧАЙНЫЕ СИГНАЛЫ И ШУМЫ
Раздел 14.
СЛУЧАЙНЫЕ ПРОЦЕССЫ, ИХ ХАРАКТЕРИСТИКИ И КЛАССИФИКАЦИЯ
Все сигналы, формируемые или выделяемые в цепях радиотехнических систем, являются случайными. Случайный характер сигналов обусловлен воздействием на источники сигналов различных по своей природе и проявлениям таких, факторов, как случайный характер модуляции, разброс параметров элементов передатчика и др. Когда влияние случайных факторов является незначительным и им можно пренебречь, сигнал можно рассматривать как детерминированный, как колебание, закон изменения во времени которого задан. Случайный сигнал описывается случайной функцией времени. Такой же характер имеют и шумы - сторонние колебания не несущие информации. Анализ случайных сигналов и шумов должен проводиться с привлечением методов теории случайных процессов. Примеры случайных процессов приведены на рис. 14.1.
14.1. Детерминированные и случайные сигналы
Детерминированный сигнал задается функцией времени или правилом его получения. Применительно к детерминированным термин «сигнал» обычно и используется как эквивалент временной функции, описывающей колебание. Примерами детерминированных сигналов являются (см. часть 1): импульсный сигнал
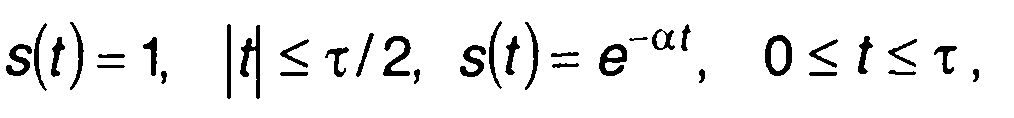(14.1)
гармоническое колебание
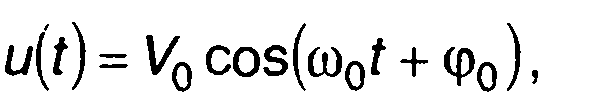(14.2)
где V0, ω0, φ0 - амплитуда, частота и начальная фаза; гармонический модулированный сигнал
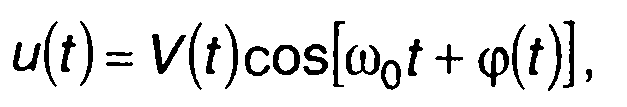(14.3)
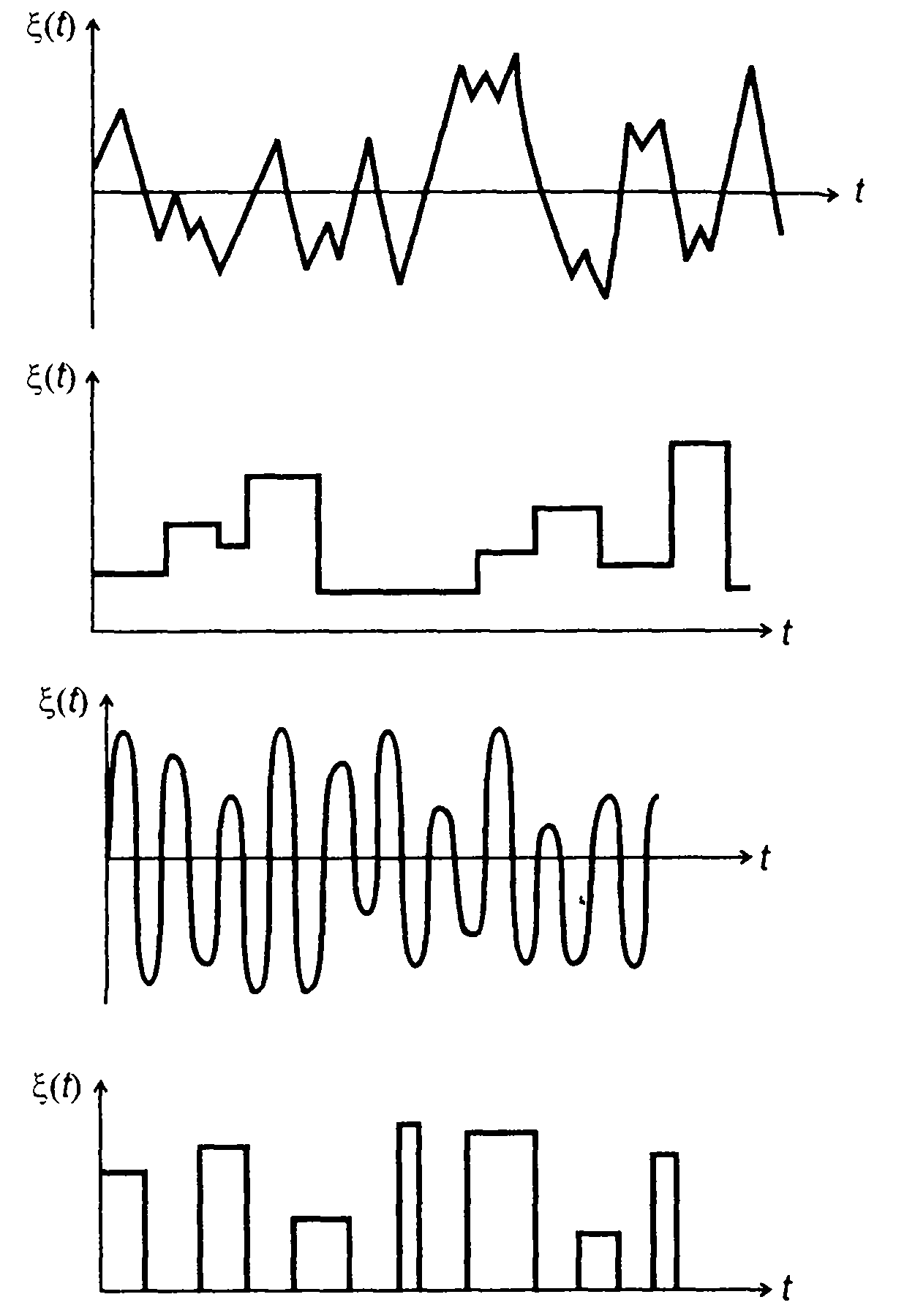
Рис. 14.1
где V(t), φ(t) - изменяемые во времени параметры; кодированный сигнал
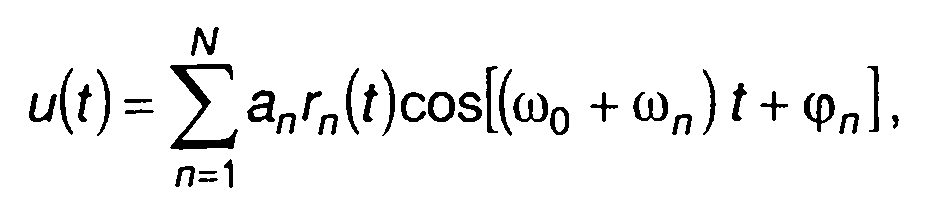(14.4)
где ап, ω0 +ωп, φп- амплитуда, частота и начальная фаза гармонического колебания длительности Т на интервале (n-1)T≤t ≤ nТ; ω0 - несущая частота; rn(t) - функция, описывающая форму импульса.
Последовательности символов: амплитуд {ап}, фаз {φп) и частот {ωп} составляют кодовые последовательности, которые определяют закон изменения параметров колебания.
Функция, описывающая сигнал s(t), может быть представлена в виде взвешенной суммы более простых (базисных) функций φп(t)
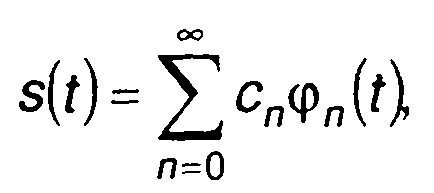(14.5)
где сn - постоянные коэффициенты.
Разложение s(t) по ортогональной системе функций {φn(t)}назы- вается обобщенным рядом Фурье. Совокупность коэффициентов разложения представляет спектр сигнала.
Возможно также интегральное преобразование s(t). Наиболее часто при анализе сигналов применяется преобразование Фурье
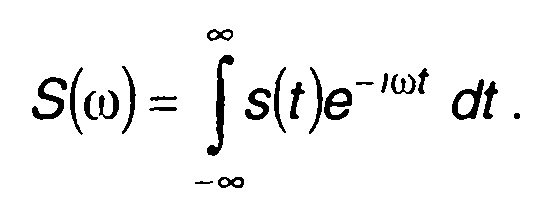(14.6)
Ему соответствует обратное преобразование
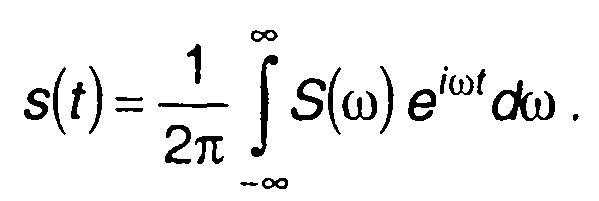(14.7)
Функция S(ω) называется спектральной плотностью, или спектром сигнала.
Непрерывные сигналы могут задаваться выборочными значениями - значениями, взятыми в определенные моменты времени (как правило, через заданный постоянный интервал времени). Получаемый таким образом сигнал называется дискретным. Дискретные сигналы имеют вид последовательности коротких импульсов, амплитуды которых соответствуют мгновенным значениям непрерывного сигнала s(t)
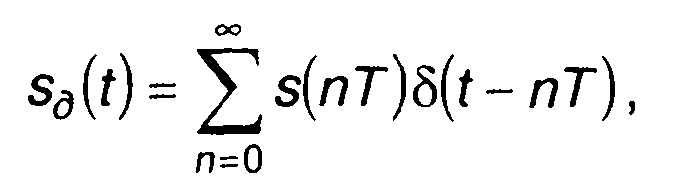(14.8)
где T- интервал дискретизации; δ(t) - импульсная функция.
Случайный сигнал представляет случайное изменение во времени параметра колебания, случайный процесс. На выходе
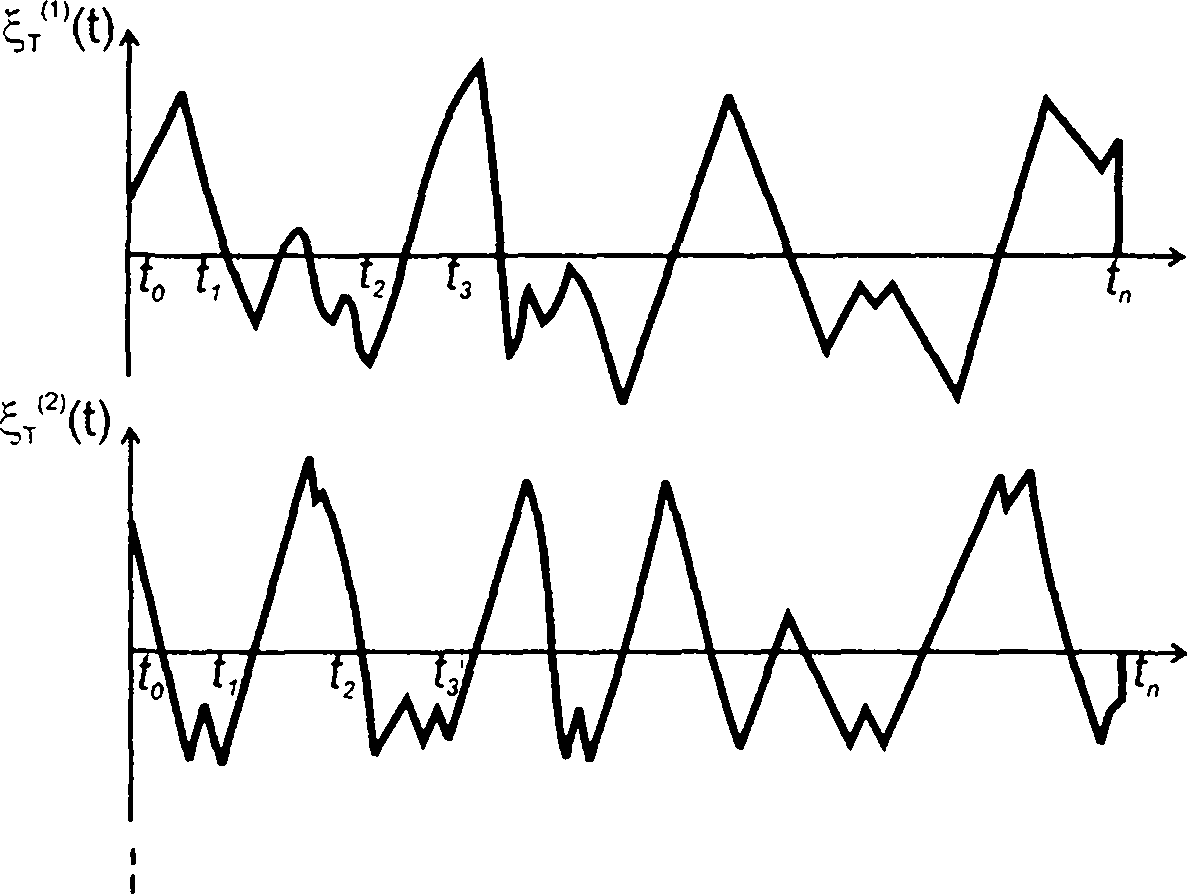
идентичных источников случайный сигнал, в отличие от детерминированного, имеет различный вид. Случайное колебание на выходе одного источника называется реализацией случайного процесса. Примером реализации может служить осциллограмма случайного сигнала при однократной развертке ЭЛО (рис. 14.2,а). Совокупность реализаций, полученных на выходе идентичных по своим характеристикам источников, представляет множество, или ансамбль реализаций. Ансамбль реализаций имеет вид осциллограммы случайного сигнала при периодической развертке ЭЛО (рис. 14.2,6).
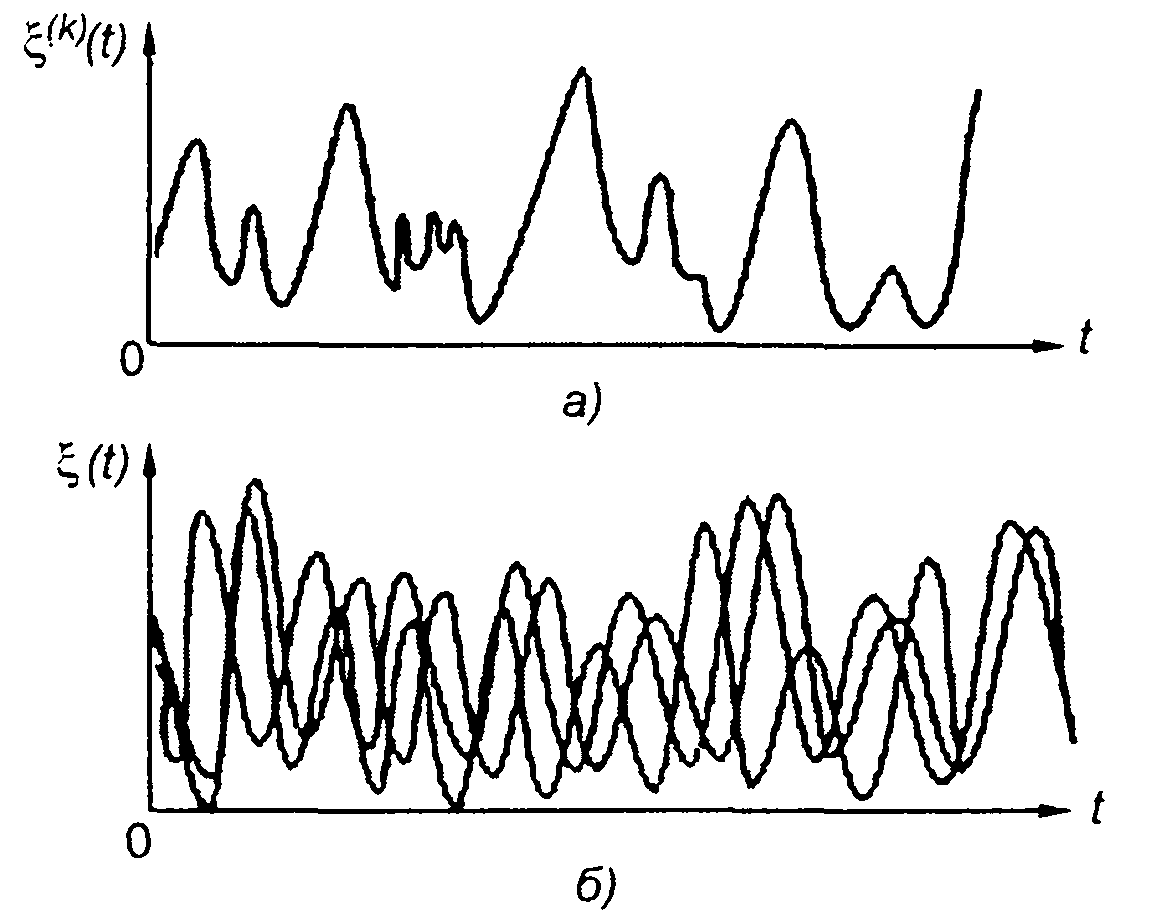
Рис. 14.2
Описать случайный сигнал с помощью временной функции невозможно - любая временная функция, описывающая отрезок реализации на выходе одного источника сигнала, не соответствует сигналу на выходе другого идентичного источника. Случайные сигналы поддаются описанию только статистически - с использованием вероятностных характеристик или характеристик, функционально с ними связанных. Такими характеристиками являются функция распределения, плотность распределения вероятностей или моменты распределения.
Особенности случайных сигналов не позволяют применить к ним непосредственно интегральные преобразования. Преобразование Фурье, как инструмент анализа, используется применительно к корреляционной функции, определяет спектральную плотность мощности случайного сигнала. Такое же положение сохраняется и в отношении дискретных случайных сигналов - по дискретным
значениям можно восстановить только реализацию (отрезок реализации) случайного сигнала.
Отразить общие черты и отличия детерминированных и случайных сигналов позволяет и их геометрическая интерпретация. При обобщенном спектральном анализе детерминированный сигнал представляется в виде ряда по ортогональной системе функций
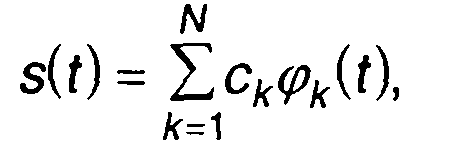(14.9)
где ск - постоянные коэффициенты; {φk(t)} - ортонормированная
система функций.
Свойство ортогональной системы функций:
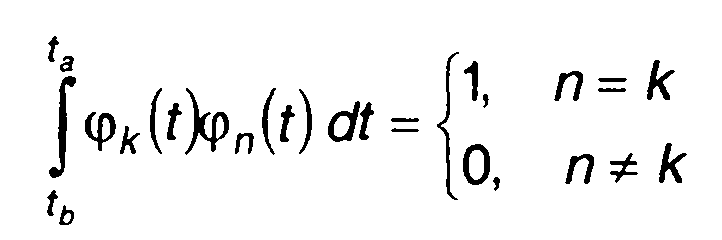(14.10)
позволяет получить выражения для коэффициентов разложения в виде
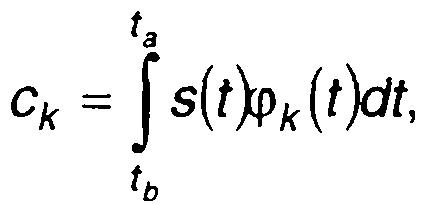(14.11)
где [ta, tb ] - интервал ортогональности функций φk(t).
Ортонормированная система базисных функций {φk(t)} образует координатную систему в N-мерном евклидовом пространстве. Функции φk(t) представляют единичные векторы, коэффициенты ск - проекции вектора s(t) на оси координат. Сигнал, описываемый (14.9), рассматривается как N-мерный вектор (рис. 14.3,а).
Выбор базисной системы функций определяет систему координат. Замена системы базисных функций означает смену системы координат.
Векторы определены только тогда, когда они имеют конечную длину
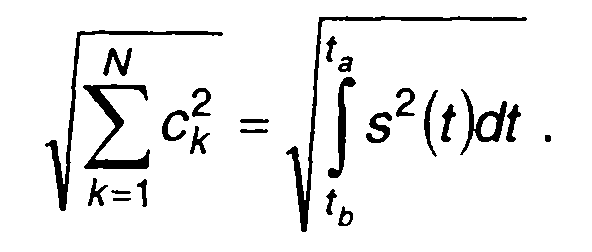(14.12)
Из (14.12) следует, что геометрическую трактовку допускают только сигналы с конечной энергией.
Рассматривая случайный процесс, выделяем отрезок реализации ξt(k)(t) (рис. 14.3,6). На выделенном интервале времени
можем рассматривать как заданную функцию времени. При выполнении некоторых условий ее можем представить в виде обобщенного ряда Фурье, аналогичного (14.9). Ограничиваясь конечным числом членов ряда, запишем
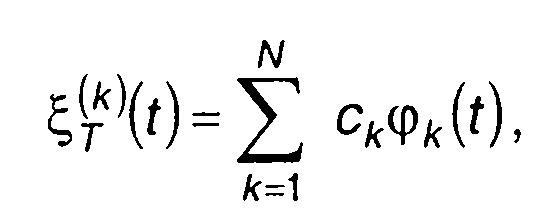(14.13)
где сk - коэффициенты разложения; {φk(t)} _ система ортонормированных функций.
Коэффициенты разложения определяются, как и в (14.11)
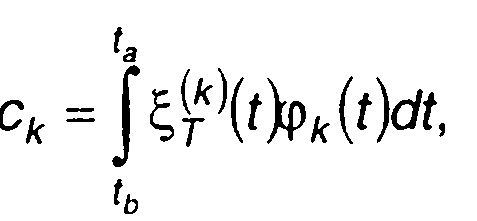(14.14)
где [ta, tb] - интервал ортогональности функцийφk{t).
Для выделенного отрезка реализации коэффициенты разложения сk определяются (14.14) однозначно. Они описывают вектор в евклидовом пространстве (рис. 14.3,6). Для другой реализации коэффициенты будут уже иными, они описывают другой вектор в том же пространстве. При рассмотрении множества реализаций коэффициенты должны рассматриваться как случайные величины, которым соответствует случайное множество векторов. Нахождению конца вектора в заданной области пространства соответствует определенная вероятность.
14.2. Шумы
Формирование, передача и прием сигналов всегда сопровождаются сторонними колебаниями (колебаниями, не несущими информации) - шумом. Источниками шума являются все типы резисторов, полупроводниковые приборы (диоды, триоды и др.), электронные и газоразрядные приборы, фотоэлементы, фотоумножители и т.д., т.е. активные и пассивные элементы радиотехнических цепей.
Шум в резисторах представляет флуктуации напряжения (тока), объясняется случайным характером теплового движения
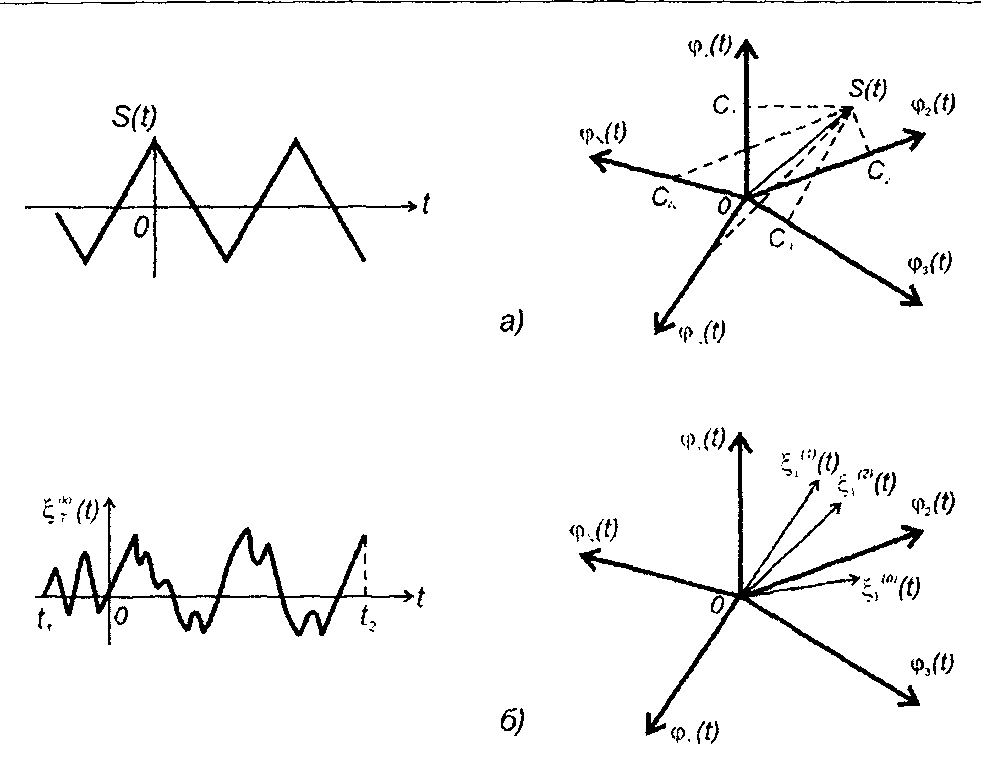
Рис. 14.3
электронов. Поэтому эти флуктуации называются тепловым шумом. Квадрат эффективного напряжения теплового шума в полосе частот ∆f определяется формулой Найквиста
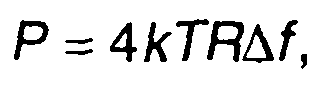(14.15)
где k - постоянная Больцмана (k= 1,38-10’23 Дж/град); T- температура источника шума; Я - сопротивление нагрузки.
Более точно формула Найквиста может быть записана в виде
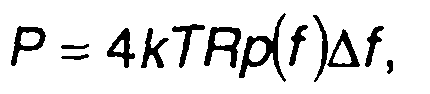(14.16)
где p(f) - коэффициент Планка:
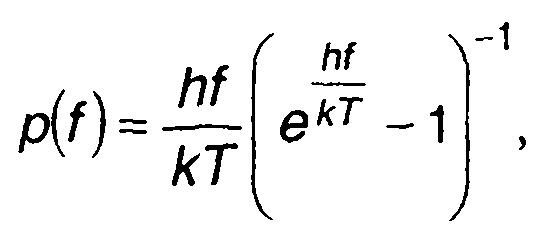(14.17)
где h - постоянная Планка (h = 6,62*10-34 Дж * с).
Источником флуктуаций, возникающих в вакуумных приборах, является случайный характер эмиссии и движения электронов
в этих элементах. Такой шум называется дробовым. Мощность шума электровакуумного диода в полосе частот ∆f на нагрузке Я определяется формулой
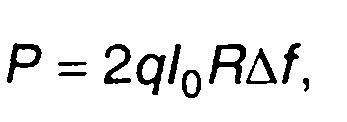(14.18)
где q- заряд электрона (q =1,6*10-19 К); l0 - среднее значение тока, протекающего через диод; ∆f - полоса шума на выходе.
В полупроводниковых приборах различают несколько составляющих внутреннего шума, основными из которых являются тепловой и дробовый шумы. Как и в других элементах, природа появления теплового шума связана с хаотичностью теплового движения заряженных частиц. Квадрат эффективного значения напряжения этой составляющей определяется формулой Найквиста. Причина появления дробового шума в полупроводниковых приборах во многом такая же, что и в вакуумных приборах.
Спектральные плотности мощности шумов различных источников отличаются весьма сильно. Так для проволочного резистора спектральная плотность мощности при комнатной температуре имеет порядок 10-21 Вт/Гц, а для тиратронов 10-4-10-5 Вт/Гц. Полоса частот, занимаемая спектром шума различных источников, изменяется в широких пределах. Спектр теплового шума - сплошной и достаточно равномерный в полосе до 1013 - 1014 Гц.
В процессе исследования шум должен рассматриваться как случайный процесс, и к нему применимы методы исследования случайных процессов. Случайные сигналы и шумы объединяет их случайный характер и, следовательно, для них характерны свои, специфические методы исследования. Вследствие этого в дальнейшем случайные сигналы и шумы будут объединены терминологически и называться случайными процессами.
Содержание второй части справочного пособия определяется интересами исследования случайных колебаний в радиотехнических цепях. Поэтому в ней излагаются не просто методы теории случайных процессов, а только те из них, которые в большей степени отвечают интересам анализа случайных сигналов и шумов, и в виде, наиболее удобном для рассмотрения случайных сигналов. Специфика рассмотрения случайных процессов в справочном пособии заключается прежде всего в выборе их характеристик и очерченного круга задач исследований. Это сказывается на формировании разделов второй части книги и методике их изложения.
14.3. Основные характеристики случайных процессов
Случайный процесс представляет случайную функцию времени, и его рассмотрение во временной области, как и детерминированного сигнала, является наиболее наглядным. Однако если детерминированный сигнал однозначно описывается временной функцией, то такое описание случайного процесса невозможно (рис. 14.4). Случайный процесс в каждый момент времени представляет случайную величину, которая может принимать различные значения из области возможных. Таким образом, во временной области случайный процесс может быть описан только с использованием вероятностных характеристик. Наиболее полными из них являются функция распределения вероятностей (ФРВ) или плотность распределения вероятностей (ПРВ). В зависимости от того, сколько моментов времени выбирается при описании случайного процесса, различают ФРВ различной мерности (в общем случае n-мерные) Fn(х1, x2, .... хn).
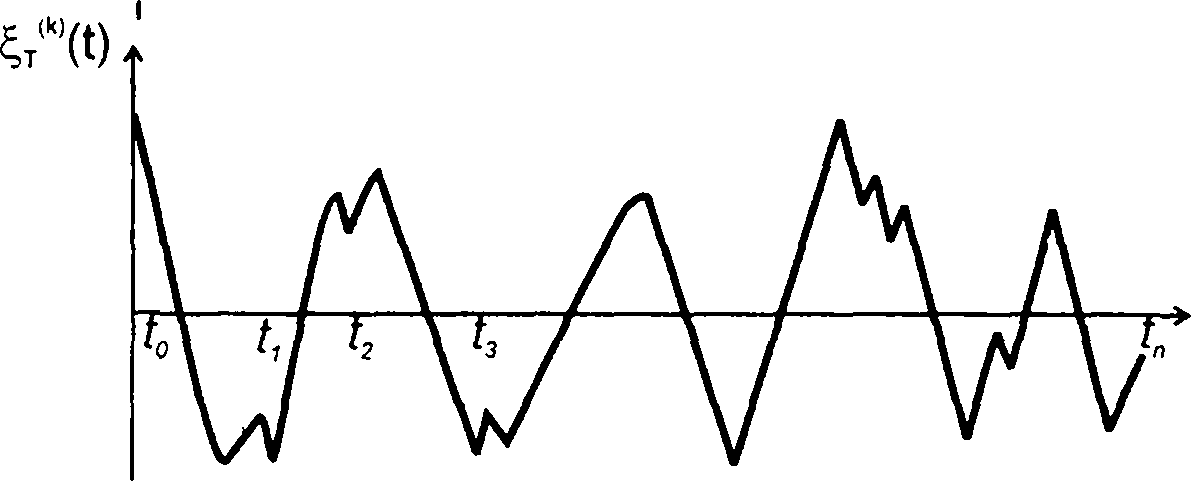
От ФРВ можно перейти к ПРВ
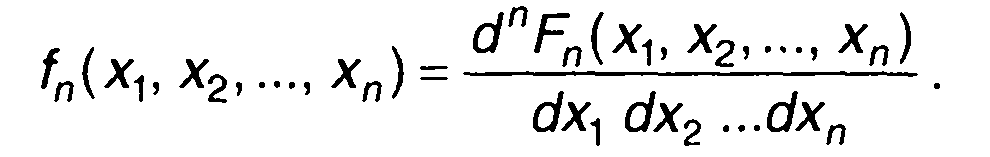(14.19)
При описании случайных процессов используются и менее полные характеристики - моменты распределения
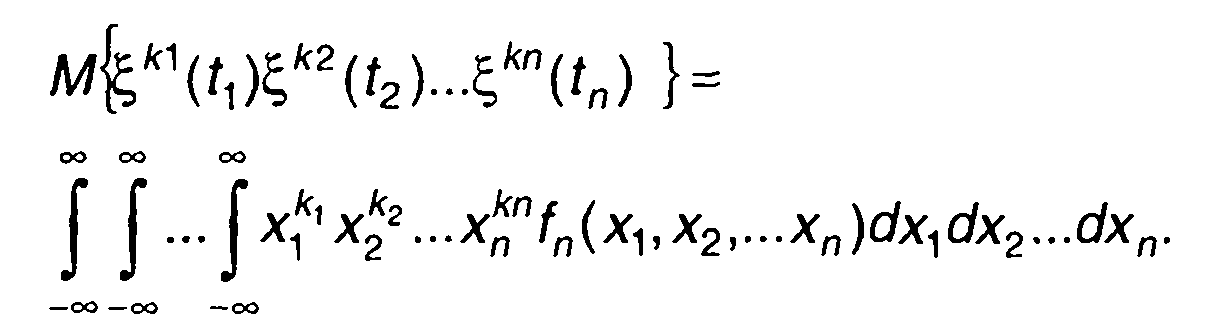(14.20)
Начальный момент первого порядка - математическое ожидание
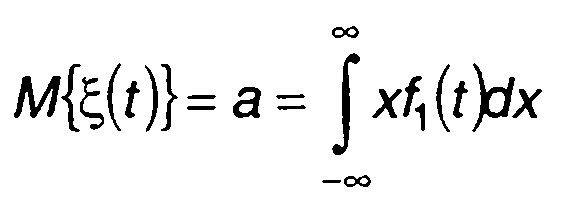(14.21)
описывает постоянную составляющую случайного сигнала. Второй центральный момент - дисперсия
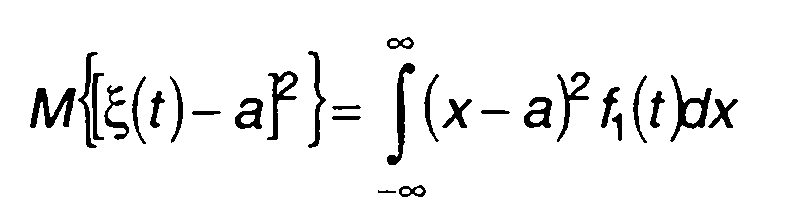(14.22)
- мощность переменной составляющей.
Важное место при анализе случайных процессов занимает второй смешанный центральный момент распределения вероятностей - корреляционная функция.
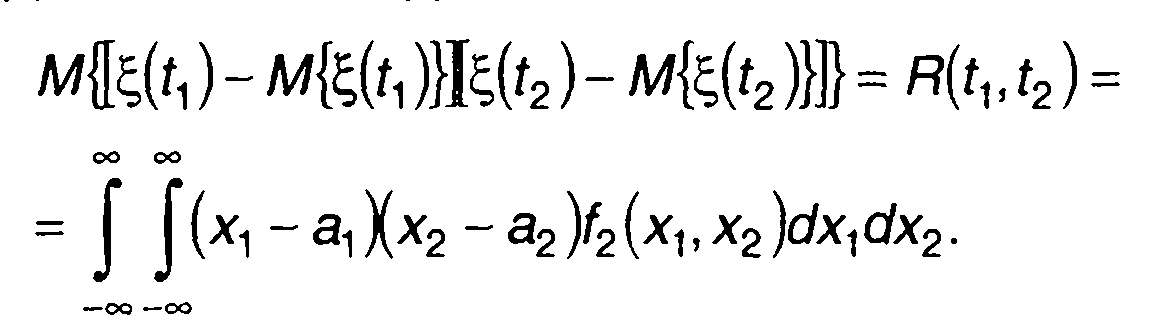(14.23)
Корреляционная функция описывает степень статистической связи значений случайного процесса или двух случайных процессов, взятых в два различных момента времени.
Характеристики распределения для широкого класса случайных процессов (эргодических случайных процессов) могут быть получены в результате обработки одной реализации. Так математическое ожидание и дисперсия случайного процесса могут быть определены как
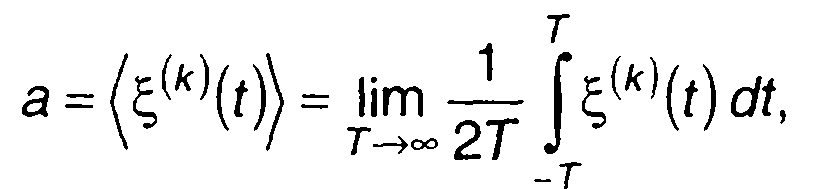(14.24)
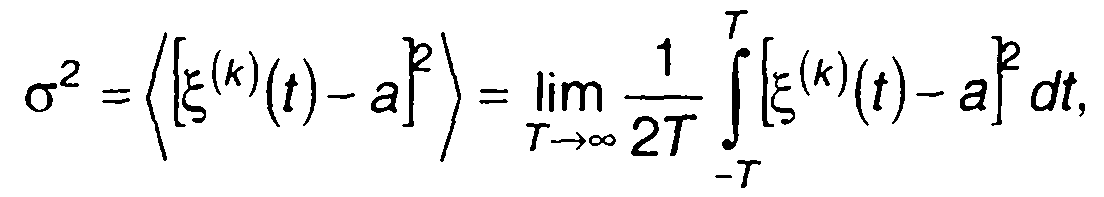(14.25)
где ξ,(k)(t) - реализация случайного процесса; <...> - символ усреднения по времени.
Дата добавления: 2015-12-16; просмотров: 1686;