ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 15 страница

Корреляционная функция эргодического случайного процесса описывается выражением

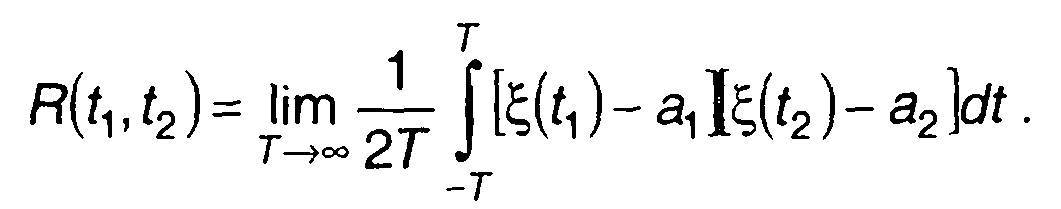(14.26)

Полезной характеристикой при описании случайного процесса является характеристическая функция, она определяется как сред­нее значение функции e^ivξ(t) где v- действительная величина, вы­ражением

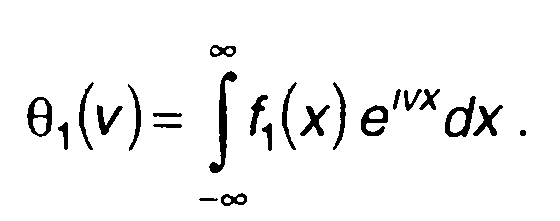(14.27)

Выражение (14.27) представляет преобразование Фурье ПРВ. Следовательно, от характеристической функции можно осущест­вить переход к ПРВ с помощью обратного преобразования

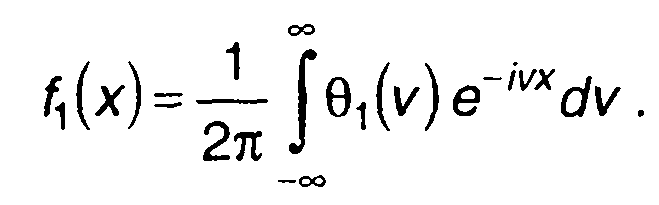(14.28)

Распространив понятие характеристической функции на сово­купность случайных величин ξ(t₁), ξ(t₂),...,ξ(t_n), выражение для n-мерной характеристической функции запишем в виде

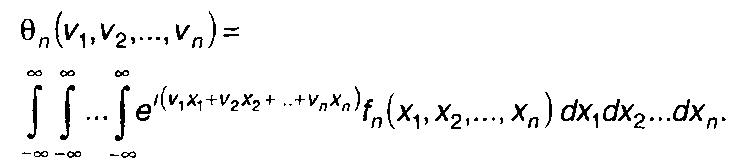(14.29)

Обратный переход от характеристической функции к n-мерной ПРВ определяется выражением

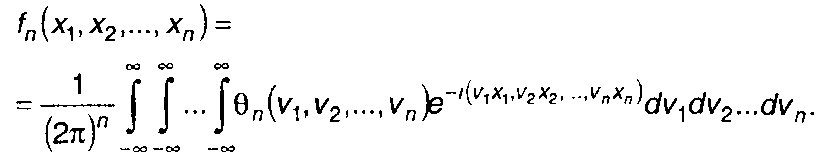(14.30)

Удобство использования характеристической функции связано в первую очередь с ее мультипликативным свойством е^х+у = е^хе^у.

Указанные характеристики могут быть распространены на сово­купность случайных процессов.

Реализация непрерывного случайного процесса может рассмат­риваться как случайное колебание относительно выбранного уров­ня х (рис. 14.5).

Выбросы случайного процесса относительного этого уровня ха­рактеризуют поведение случайного процесса во времени и часто требуют самостоятельного исследования. К основным характери­стикам выбросов, которые определяются при анализе случайных процессов, относятся: ФРВ или ПРВ длительности положитель­ных (над выбранным уровнем) и отрицательных выбросов, средняя

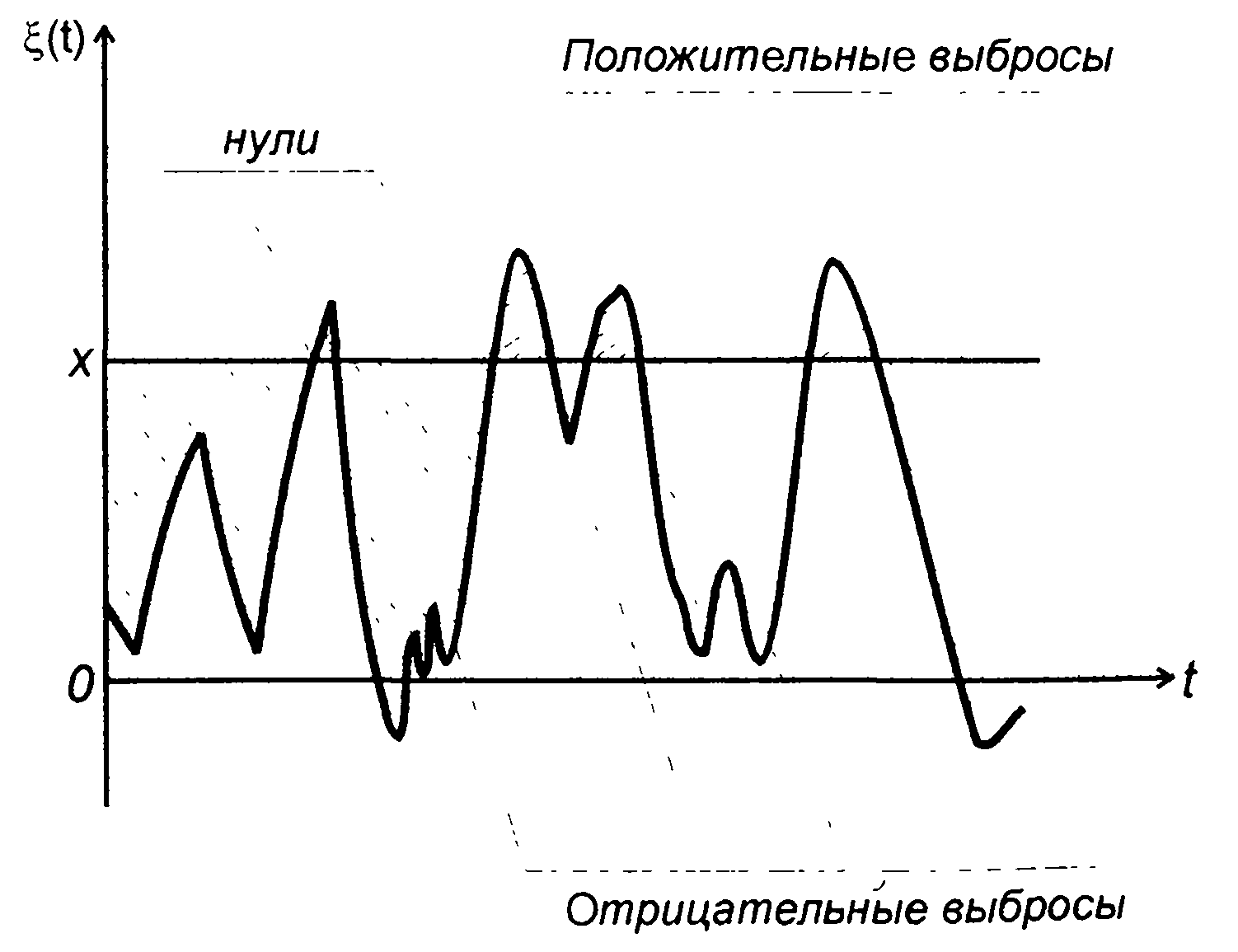
Рис. 14.5

частота следования выбросов, средняя частота экстремумов и др. Анализ выбросов, определение их характеристик является одной из составных частей общего анализа случайных процессов.

При анализе детерминированных сигналов исключительно по­лезным оказалось использование преобразования Фурье времен­ной функции, описывающей сигнал. Исследование переводится в частотную область, математические операции часто упрощаются. Преобразование Фурье непосредственно случайных процессов, как правило, невозможно, не выполняется условие существования преобразования Фурье. Используется преобразование Фурье кор­реляционной функции случайного процесса. Оно определяет спек­тральную плотность мощности случайного процесса. Корреляцион­ная функция и спектральная плотность мощности связаны друг с другом парой преобразований Фурье

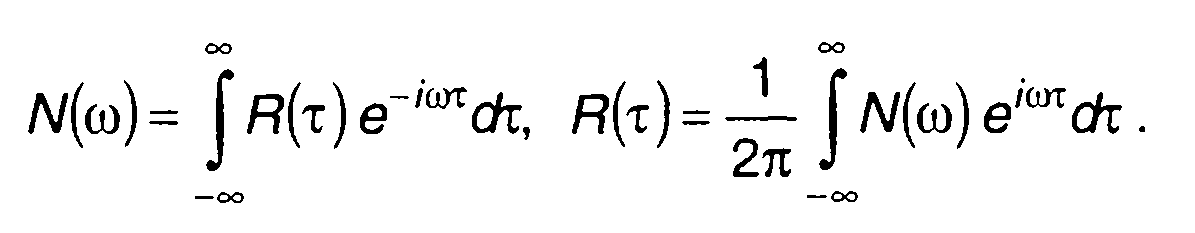(14.31)

Соотношения (14.31) лежат в основе спектрального анализа случайных процессов. Спектральный анализ - важная часть общего анализа случайных процессов.

С учетом изложенного в дальнейшем проводится описание и анализ основных характеристик случайных процессов во времен­ной и частотной областях. При их рассмотрении необходимо иметь в виду, что все характеристики случайных процессов взаимосвяза­ны, они отражают одни и те же свойства случайного процесса, только описываются с использованием различных подходов.

14.4. Классификация случайных процессов

В зависимости от природы (источника) колебаний, характеристик устройства, на выходе которого наблюдается колебание, и ряда других факторов случайные процессы могут обладать разными свойствами. Из всего возможного разнообразия случайных процес­сов выделим только те, которые наиболее часто встречаются в ин­женерной и исследовательской практике, и проведем их классифи­кацию по основным признакам. Такая классификация позволяет определить место каждого вида случайного процесса среди воз­можного их разнообразия и ввести терминологию, которая будет использована в дальнейшем.

Различают непрерывные и дискретные случайные процессы (рис. 14.6). Непрерывный случайный процесс (его реализация) может

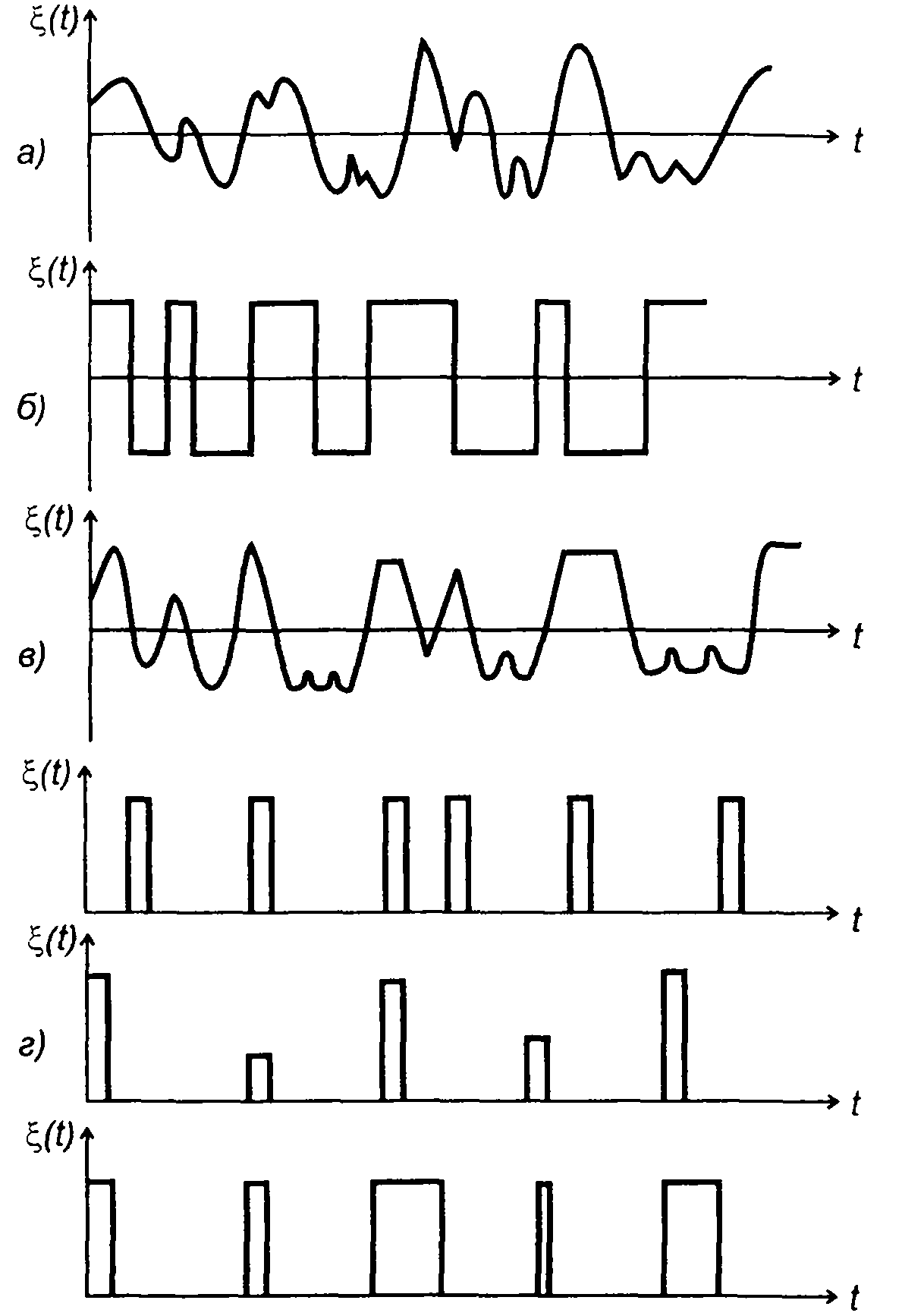
Рис. 14.6

иметь любое значение из области возможных (рис. 14.6,а). Приме­ром непрерывного случайного процесса служит шум в радиотехни­ческой цепи. Дискретный случайный процесс принимает только оп­ределенные значения. Примером такого процесса является коле­бание на выходе идеального ограничителя при подаче на его вход непрерывного случайного процесса (рис. 14.6,б).

Возможен случайный процесс смешанного типа, например, слу­чайный процесс на выход ограничителя с заданными порогами огра­ничения (рис. 14.6,в). Как сложилось на практике, дискретными будем также называть случайные процессы, получающиеся при дискрети­зации непрерывных случайных процессов во времени. Такие случай­ные процессы представляют периодическую последовательность

коротких импульсов, амплитуды которых соответствуют мгновенным значениям исходного непрерывного случайного процесса. Отдельно выделяются импульсные случайные процессы (рис. 14.6,г).

Одним из важных признаков, по которым проводится классифи­кация, является вид распределения вероятностей случайного про­цесса. Широкий класс случайных процессов составляют гауссов­ские процессы - случайные процессы с нормальным распределе­нием мгновенных значений (рис. 14.7,а). Нормальное распределе­ние является тем предельным видом, к которому при определенных условиях стремятся все другие виды распределения. Указанным обстоятельством в большой степени объясняется то важное место, которое занимают гауссовские процессы в практике исследований. Некоторые виды распределений получаются при преобразовании нормального закона распределения. Так можно получить релеевский закон распределения (рис. 14.7,б) и другие.

Наиболее полной характеристикой случайного процесса являет­ся его n-мерная ФРВ, или n-мерная ПРВ, описывающие случайный процесс в различные моменты времени. Из общего класса случай­ных процессов выделяют случайные процессы, которые полностью характеризуются ФРВ (ПРВ) первого и второго порядков (от них можно перейти к ФРВ (ПРВ) любого порядка). Если случайный про­цесс полностью описывается одномерной ФРВ (ПРВ), то он назы­вается совершенно случайным.

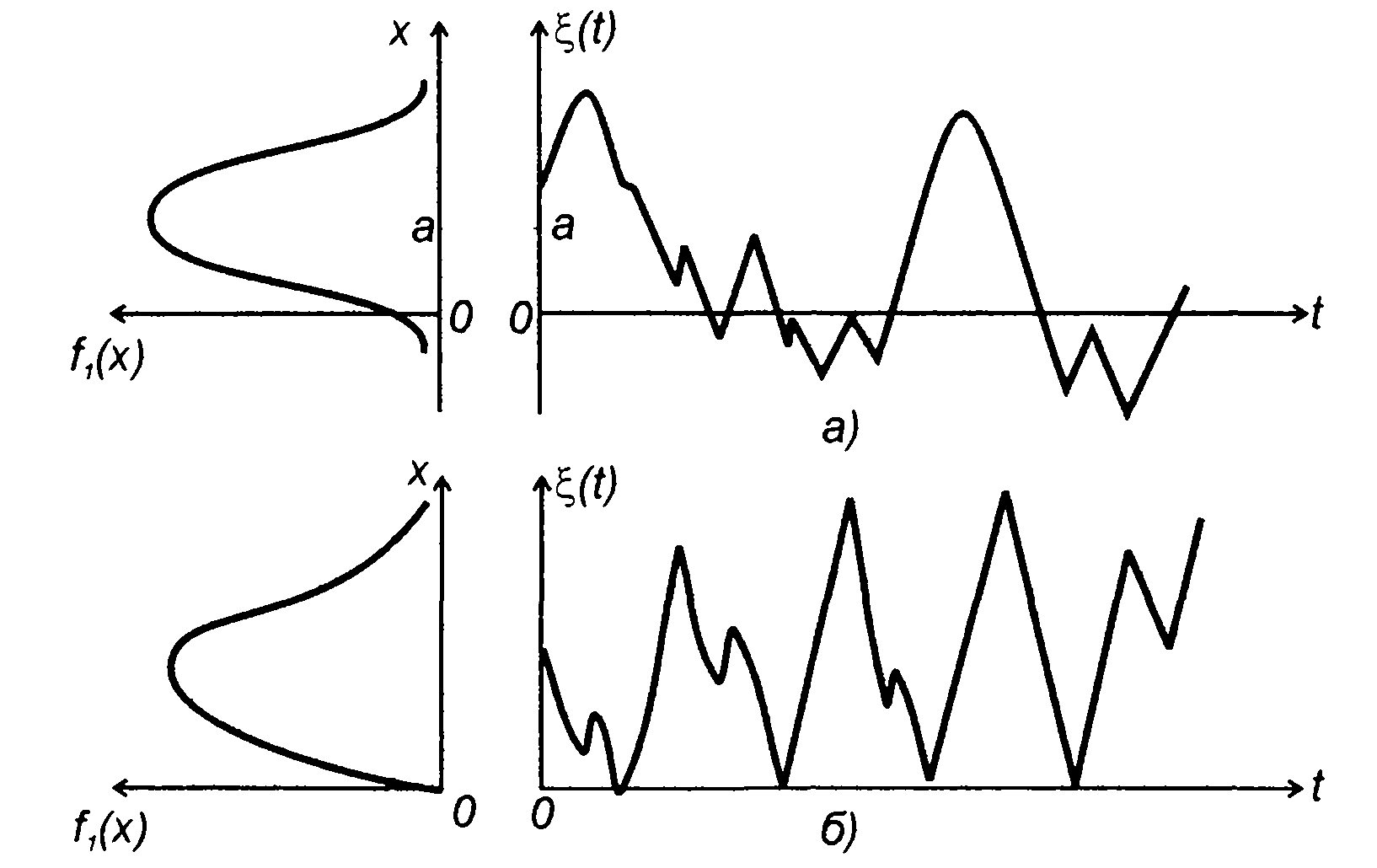
Рис.14.7

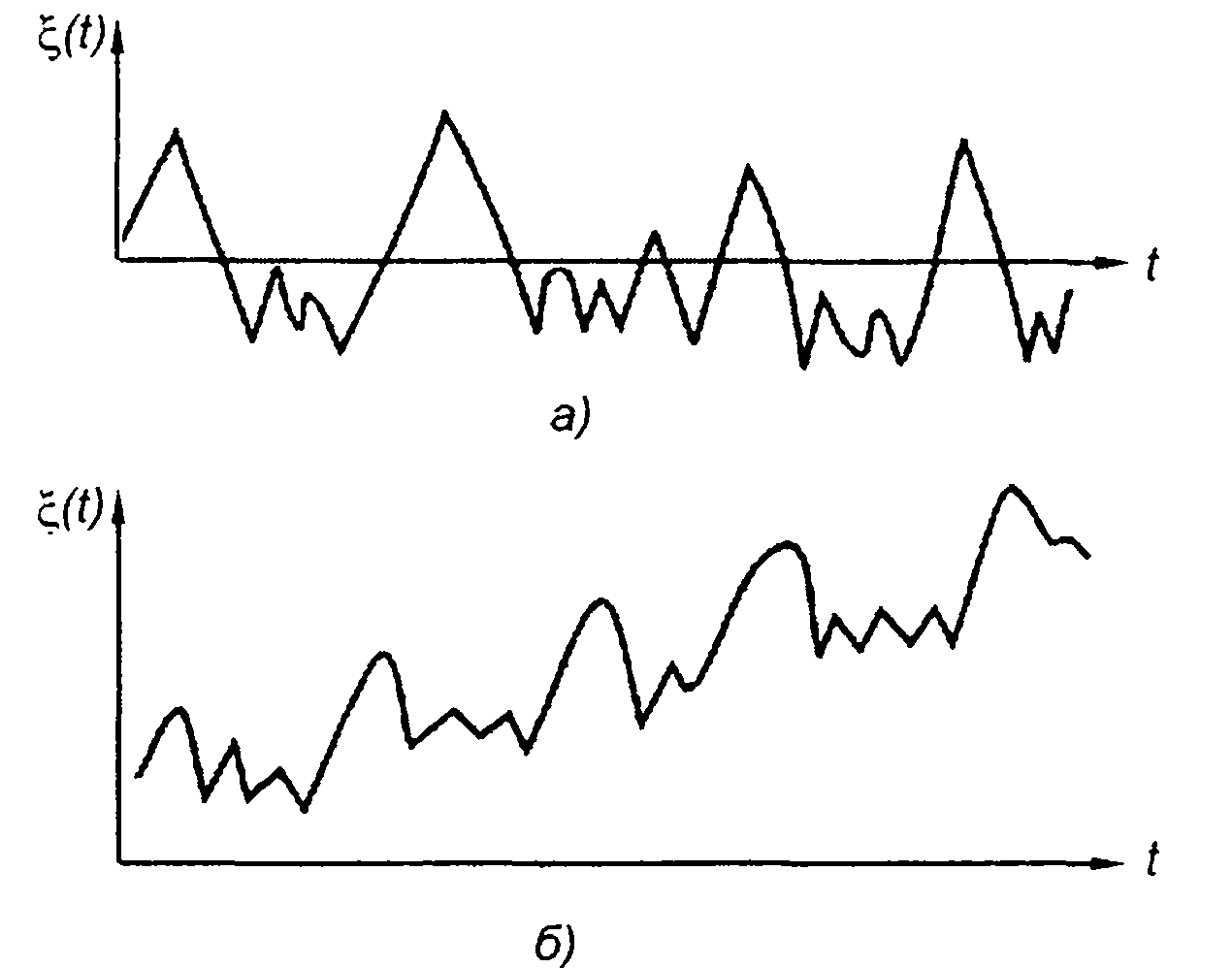
Рис.14.8

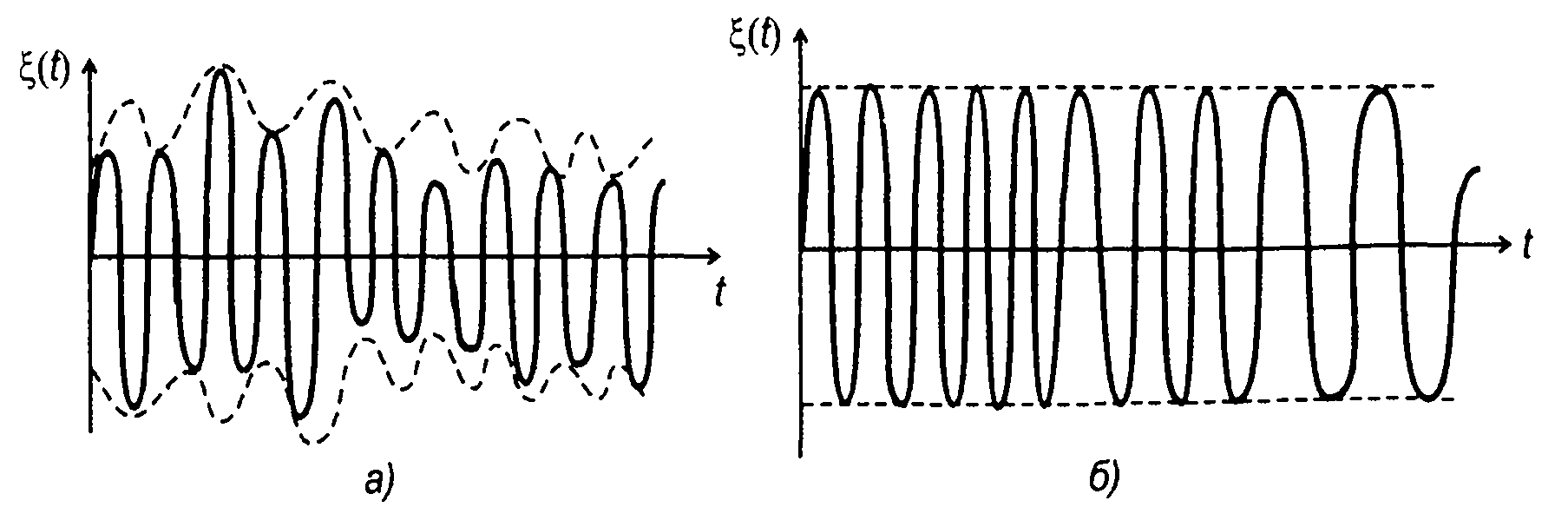
Рис. 14.10

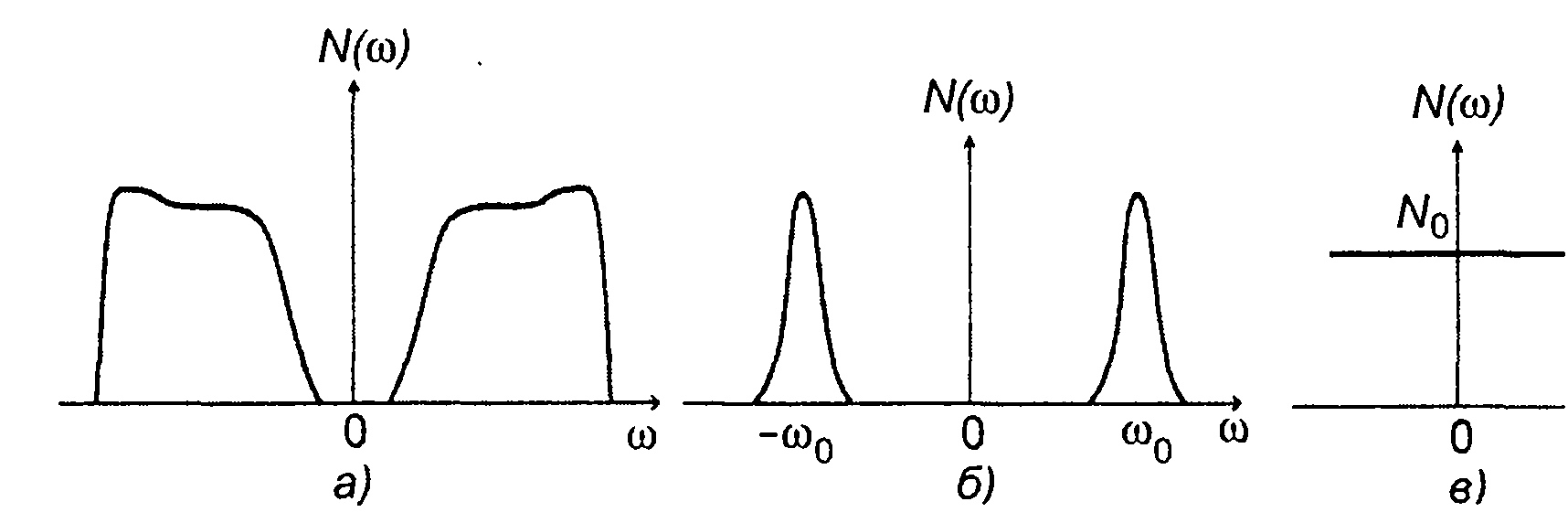
Рис. 14.9

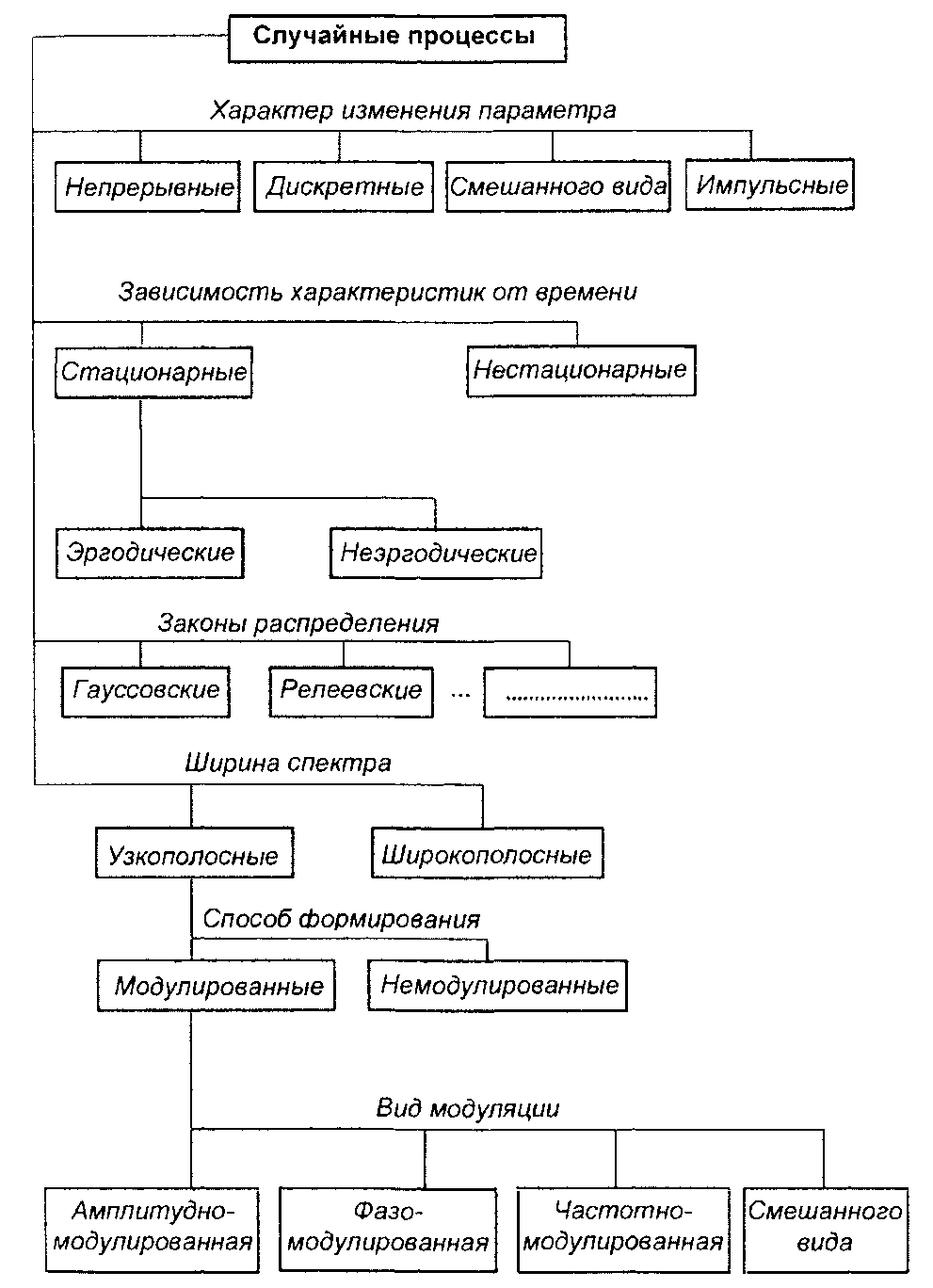
Рис. 14.11

Одним из признаков классификации случайных процессов явля­ется постоянство их характеристик во времени. Различают стацио­нарные (рис.14.8,а) и нестационарные (рис. 14.8,б) случайные про­цессы. Случайный процесс называется стационарным, если его ФРВ любого порядка не зависят от выбора начала отсчета на оси времени.

В классе стационарных случайных процессов особое место за­нимают эргодические случайные процессы. Случайный процесс называется эргодическим, если любая его характеристика, полу­ченная усреднением по ансамблю реализаций, равна характери­стике, подученной при обработке одной реализаций - усреднением по времени. Выполнение этого условия означает, что поведение каждой реализации случайного процесса статистически такое же, как и всего ансамбля реализаций. Случайные процессы, не обла­дающие указанным свойством, называются неэргодическими.

В частотной области случайные процессы описываются спек­тральной плотностью мощности, или спектром (рис. 14.9,а). В зави­симости от ширины спектра выделяют (как и среди детерминиро­ванных сигналов) узкополосные и широкополосные случайные про­цессы. Случайный процесс называется узкополосным, если его спектр сосредоточен в полосе частот, значение которой значитель­но меньше средней частоты (рис.14.9,б). Из широкополосных слу­чайных процессов особо выделяют белый шум. Белым шумом на­зывается случайный процесс, имеющий равномерный на всех час­тотах спектр (рис. 14.9,в). Белый шум физически не реализуем, яв­ляется идеализацией, удобной моделью случайных процессов, с которыми приходится иметь дело на практике.

Из узкополосных процессов следует выделить модулированные случайные процессы. Они могут иметь шумоподобную несущую, модулированную как детерминированным, так и случайным сигна­лами, и случайные процессы с гармоническим несущим колебани­ем, модулированным случайным процессом. Второй вид наиболее распространен. По виду модуляции различают: случайные процес­сы с амплитудной (рис. 14.10,а), фазовой и частотной модуляцией (рис. 14.10,6).

Краткая классификация случайных процессов, приведенная вы­ше, в обобщенном виде представлена на рис.14.11. Понятия раз­личных видов случайных процессов, введенные при классифика­ции, раскрываются полнее в дальнейшем.

Раздел 15.

ОДНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛУЧАЙНОГО ПРОЦЕССА

Случайный процесс в каждый момент времени представляет случайную величину и наиболее полно описывается одномерной ФРВ или ПРВ. Менее полными характеристиками, но в ряде случа­ев достаточными для описания и анализа случайного процесса, являются моменты распределения вероятностей. Моменты позво­ляют судить только о некоторых свойствах случайного процесса, но как характеристики часто бывают более простыми и удобными при его описании. Преобразование Фурье связывает ПРВ с характери­стической функцией случайного процесса. Использование характе­ристической функции в ряде случаев позволяет упростить анализ случайных процессов.

В разделе рассматриваются характеристики случайного процес­са, описывающие его в выбранный момент времени: одномерные ФРВ и ПРВ, соответствующие моменты распределения вероятно­стей и одномерная характеристическая функция.

15.1. Одномерная функция распределения и плотность распределения вероятностей случайного процесса

Случайный процесс в выбранный момент времени t представля­ет случайную величину, принимающую значения, равные значениям реализаций (рис. 15.1). ФРВ этой величины определяется как

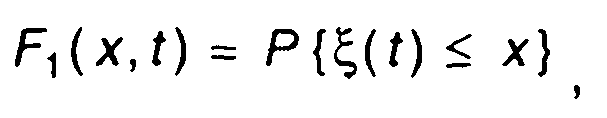(15.1)

где Р{...} - символ вероятности.

Значения F₁(x, t) лежат в диапазоне 0...1 (рис. 15.2), могут быть определены с учетом следующего предельного равенства

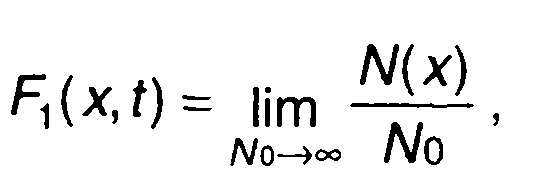(15.2)

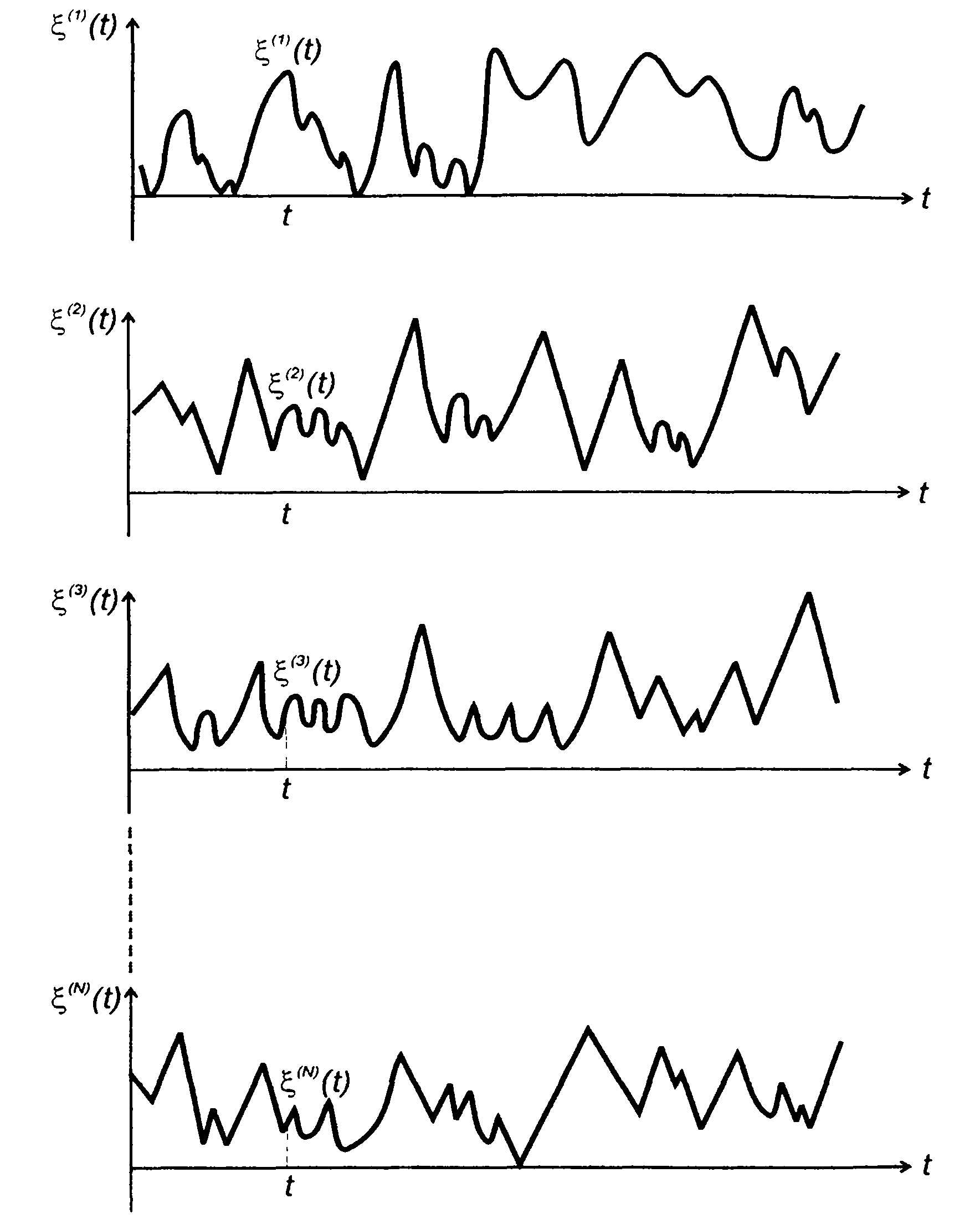
Рис. 15.1

где N₀ - общее число реализаций случайного процесса, наблюдае­мых в момент времени t, N(x) - число реализаций случайного про­цесса не превышающих уровень х в момент времени t.

Выражение (15.2) поясняет содержание ФРВ и является исходным при ее определении в процессе обработки ансамбля реализации.

Одномерное распределение вероятностей

Производная от ФРВ

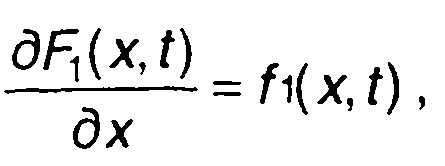(15.3)

если она существует, называется ПРВ случайного процесса (рис. 15.2). Соответственно, имея ПРВ, можно перейти к ФРВ слу­чайного процесса

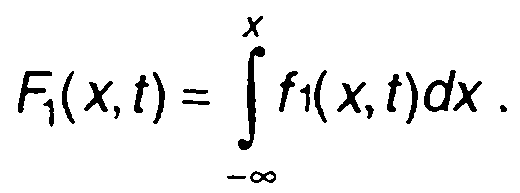(15.4)

Вероятность нахождения значений случайного процесса между уровнями x₁, и х₂ равна

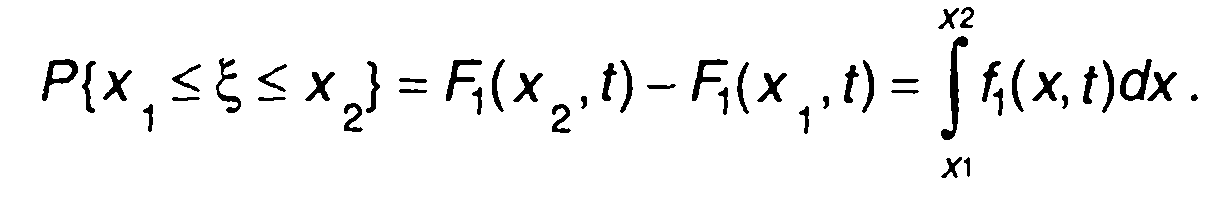(15.5)

ФРВ и ПРВ зависят от заданного уровня х и момента времени t, в который рассматривается случайный процесс. Для стационарных случайных процессов одномерные характеристики распределения от выбора момента времени t не зависят. Они зависят только от х. В дальнейшем рассматриваются стационарные случайные процес­сы, характеристики которых зависят только от х.

ФРВ дискретного случайного процесса изменяется скачкообраз­но и определяется как (рис. 15.3)

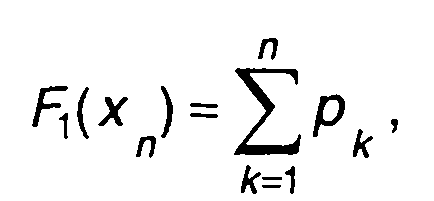(15.6)

где р_к- вероятность появления значения случайного процесса, рав­ного х_k; n- число заданных значений случайного процесса.

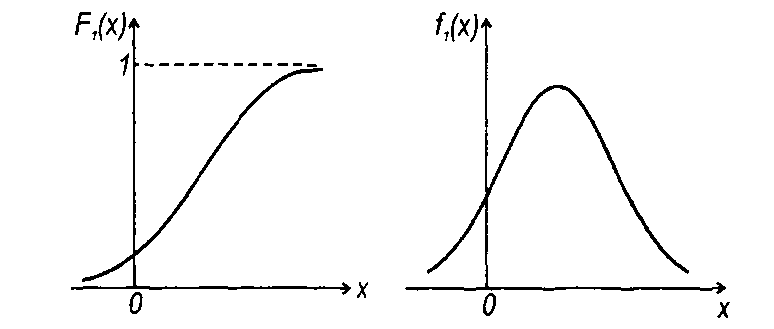
Рис. 15.2

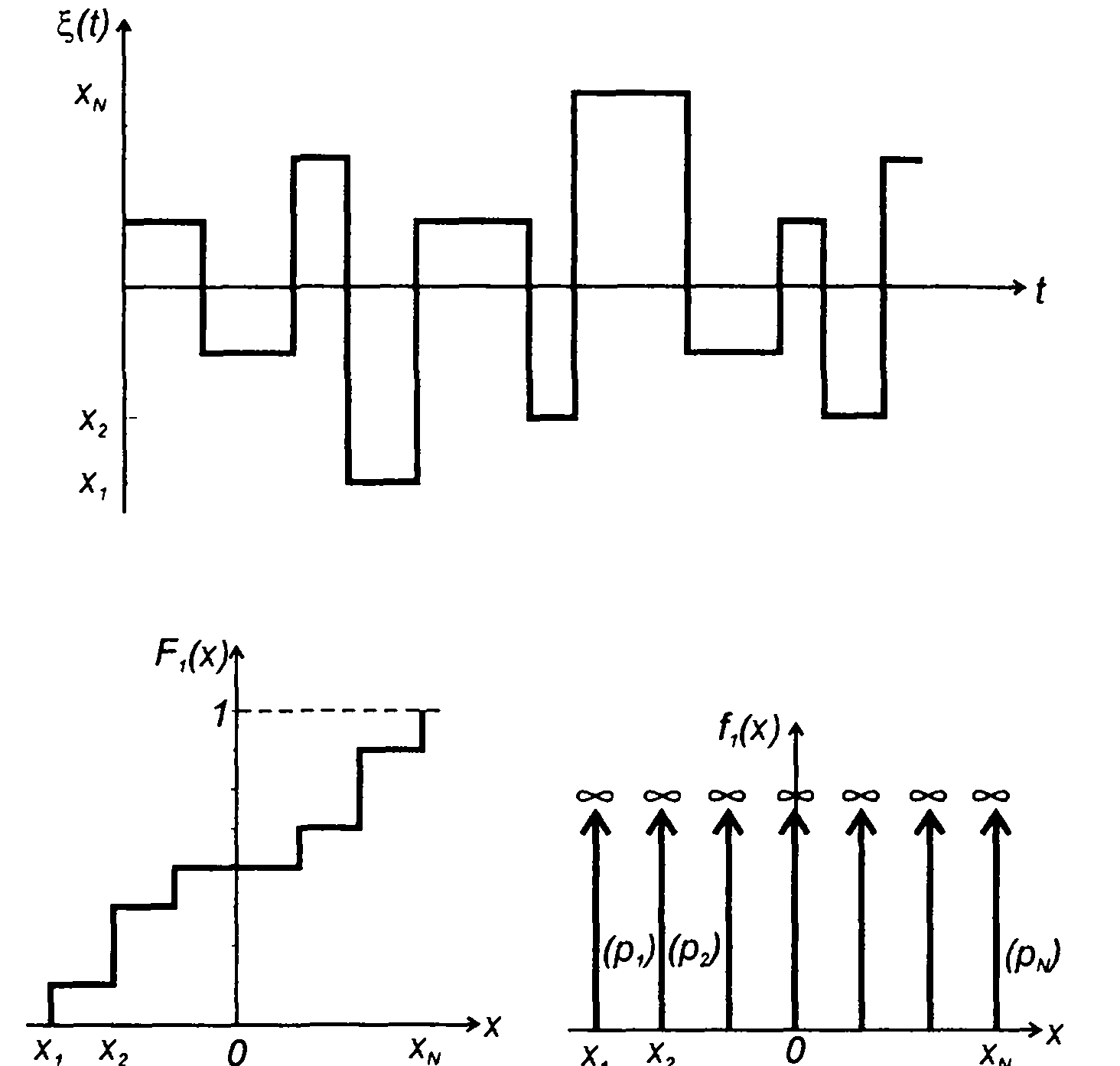
Рис. 15.3

Очевидно

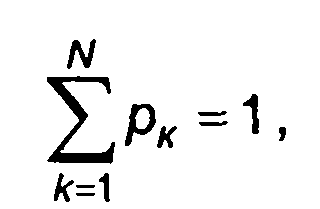
где N- число возможных значений случайного процесса.

ПРВ дискретного случайного процесса содержит импульсные функции

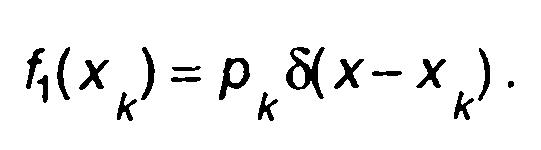(15.7)

Вероятность нахождения значений дискретного случайного про­цесса между х_n и х_т равна

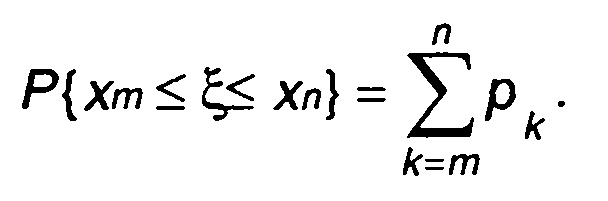(15.8)

Менее полную, но в ряде случаев достаточную информацию о случайном процессе содержат моменты распределения вероятно­стей. Начальный момент n-го порядка непрерывного случайного процесса определяется выражением

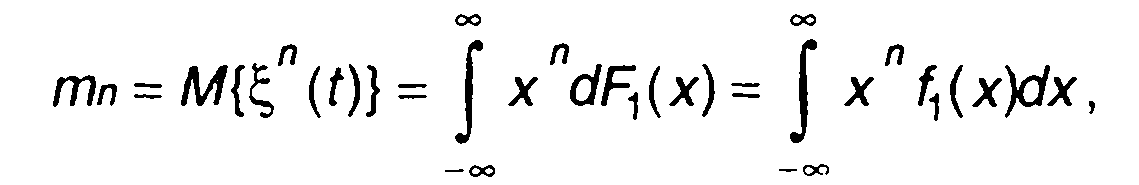(15.9)

где М{...} - символ усреднения по ансамблю реализаций.

Для дискретного случайного процесса, принимающего значения х₁ х₂ ,.., x_N c вероятностями р₁, р₂,..., р_N, имеем

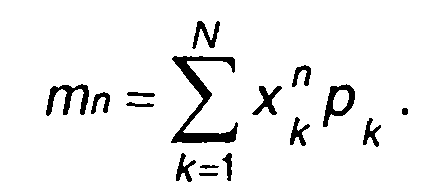(15.10)

Начальный момент первого порядка - математическое ожидание или среднее значение непрерывного случайного процесса

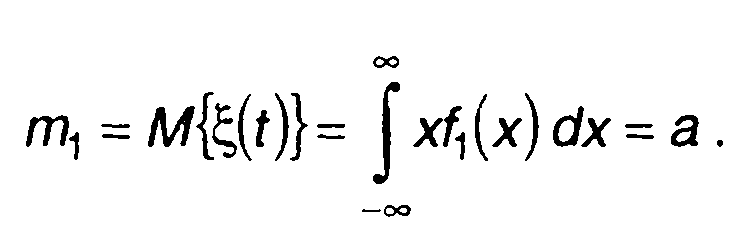(15.11)

Математическое ожидание дискретного случайного процесса оп­ределяется выражением

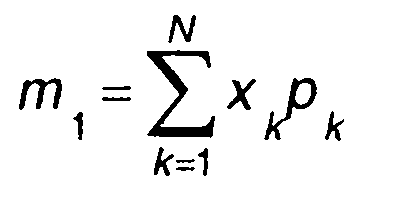(15.12)

Случайный процесс с математическим ожиданием, равным ну­лю, называется центрированным, его обозначим ξ₀(t). Переход к

центрированному случайному процессу очевиден ξ₀(t) = ξ(t) - а.

Моменты распределения вероятностей центрированного слу­чайного процесса называются центральными

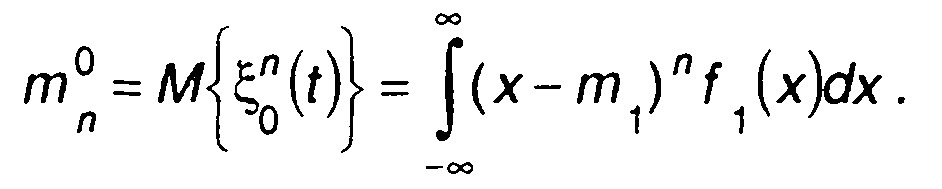(15.13)

Для дискретного случайного процесса

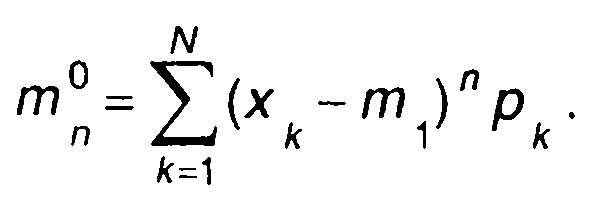(15.14)

Центральный момент первого порядка, очевидно, равен нулю. Центральный момент второго порядка называется дисперсией. Для непрерывного случайного процесса она определяется как

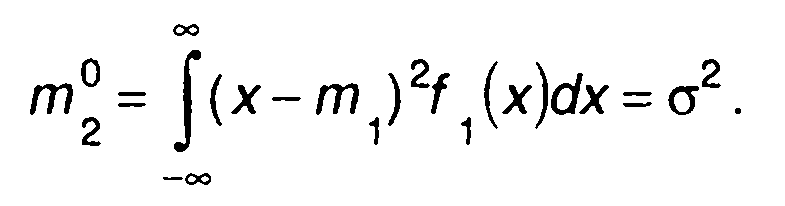(15.15)

Для дискретного случайного процесса

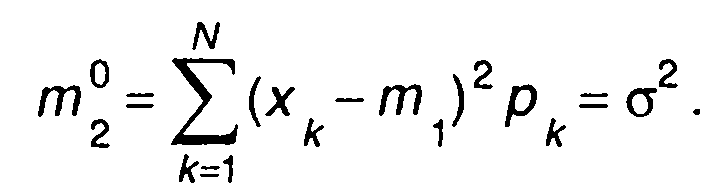(15.16)

Дисперсия характеризует степень отклонения случайного про­цесса (его мгновенных значений) от математического ожидания. Величина а называется средним квадратическим отклонением случайного процесса. Дисперсия связана с начальными моментами соотношением, получаемым из (15.15) или (15.16)

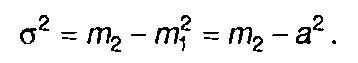(15.17)

В общем случае центральные моменты распределения вероят­ностей связаны с начальными следующими выражениями:

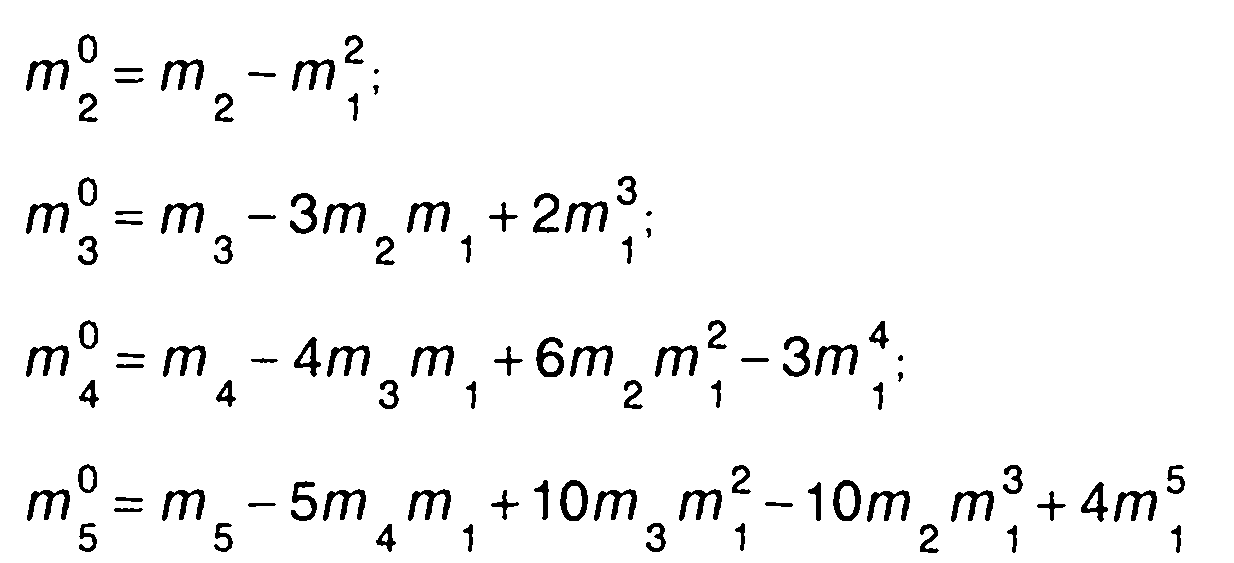(15.18)

Приведенные равенства, а также продолжение их ряда могут быть получены из (15.13)

Исходные данные, необходимые для определения характери­стик распределения, приведенных выше, получаются в результате обработки ансамбля реализаций случайного процесса. Такой под­ход к определению характеристик не всегда удобен и возможен. Вследствие этого особый интерес представляют случайные про­цессы, позволяющие получить те же характеристики при обработке одной реализации - эргодические случайные процессы .

15.2. Эргодические случайные процессы , их характеристики распределения

Среди случайных процессов особое место занимают эргодические случайные процессы. Случайный процесс называется эргодическим, если его характеристики распределения вероятностей, по­лучаемые усреднением по ансамблю реализаций, равны характе­ристикам, получаемым усреднением по времени при обработке од­ной реализации. Необходимым условием эргодичности является стационарность случайного процесса. Свойством эргодичности об­ладают практически все стационарные случайные процессы, с ко­торыми приходится встречаться на практике. В некоторых случаях эргодичность случайного процесса принимается гипотетически.

Для эргодического случайного процесса одномерная ФРВ может быть определена как (рис. 15.4)

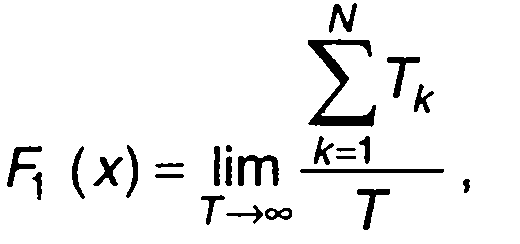(15.19)

где Т- интервал времени наблюдения; T_k - интервал времени, на котором мгновенные значения случайного процесса не превыша­ют уровень х (на рис. 15.4 - длительности незаштрихованных уча­стков).

Моменты распределения вероятностей эргодического случайно­го процесса также могут получаться усреднением по времени. Ма­тематическое ожидание находится как

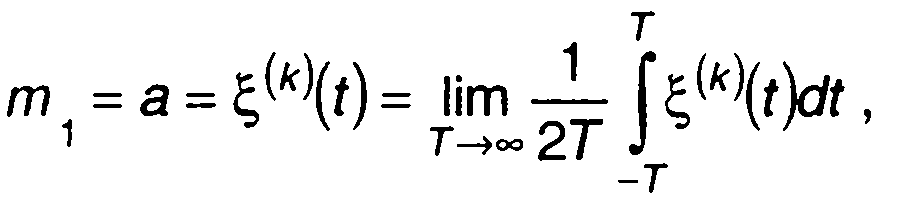(15.20)

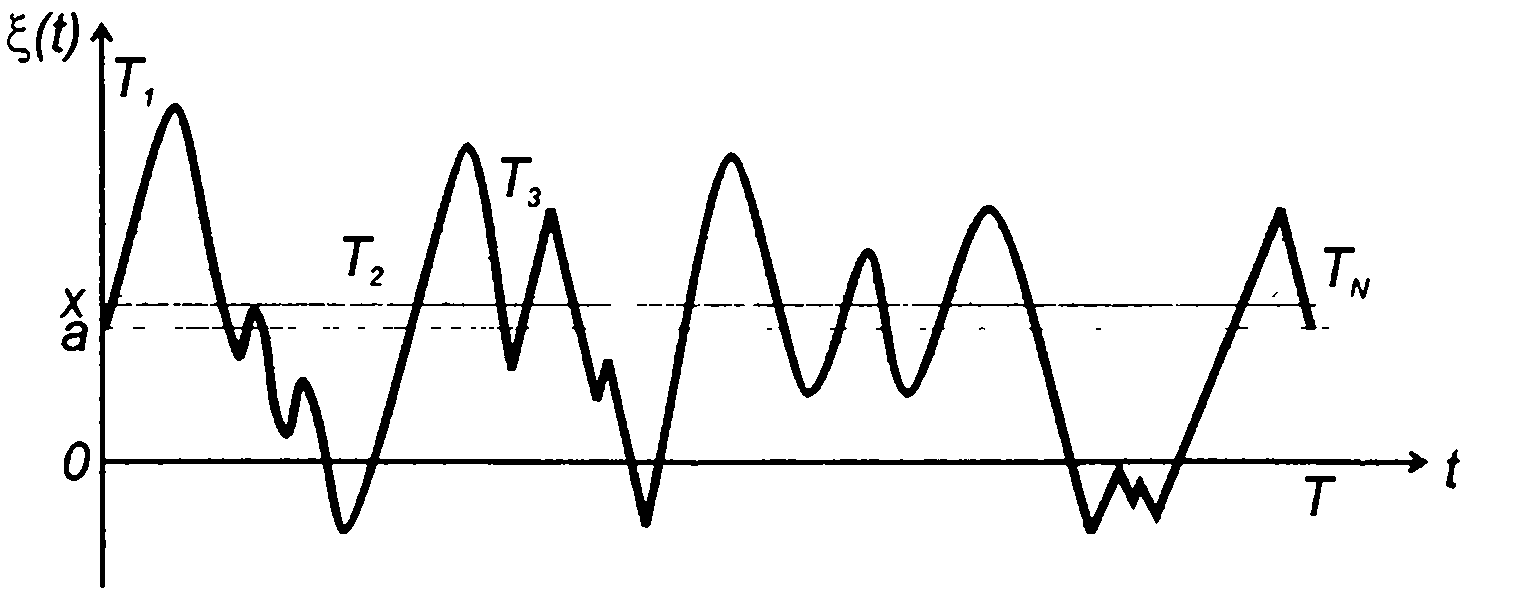
Рис. 15.4

где ξ^(к)(0 - реализация случайного процесса; - символ усред­нения по времени.

Величина (15.20) представляет постоянную составляющую слу­чайного процесса (рис. 15.4).

Второй начальный момент

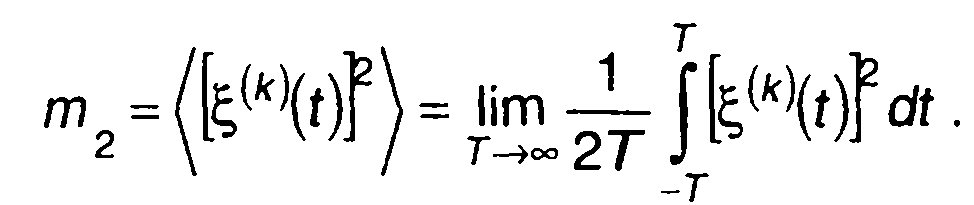(15.21)

описывает среднюю мощность случайного процесса. Средняя мощ­ность переменной составляющей (центрированного случайного процесса) определяется центральным моментом второго порядка - дисперсией

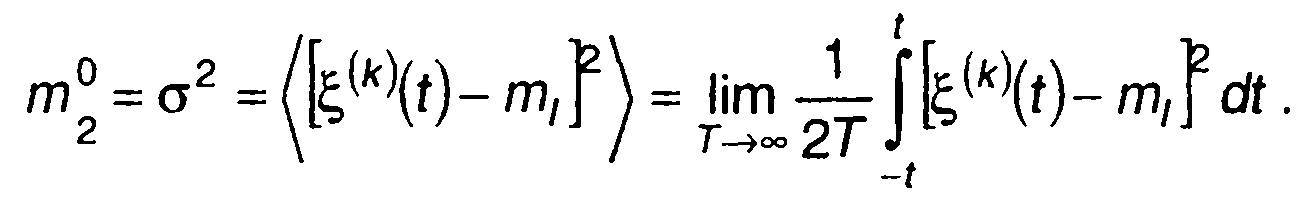(15.22)

Рассмотренные характеристики и другие, получаемые усредне­нием по времени для эргодических случайных процессов, идентич­ны получаемым из ансамбля реализации. Однако физическое со­держание характеристик эргодического случайного процесса (по крайней мере моментов распределения вероятностей первых по­рядков) является более очевидным.

15.3. Некоторые виды случайных процессов

В качестве примеров рассмотрим некоторые виды случайных процессов, их характеристики распределения вероятностей.

1. Гауссовский процесс

Одним из наиболее важных законов распределения случайных процессов является нормальный. Случайный процесс, имеющий нормальное распределение, называется гауссовским. Важное ме­сто, занимаемое гауссовским процессом, объясняется рядом при­чин, из которых следует отметить:

• гауссовский процесс принимается как математическая модель для большого числа случайных процессов с достаточно строгим обоснованием;

• нормальный закон представляет тот предельный вид, к кото­рому при некоторых условиях, часто выполняемых на практике, приближаются другие законы распределения. Это связано в первую

очередь с тем, что в соответствии с центральной предельной тео­ремой теории вероятностей распределение суммы большого числа независимых случайных величин стремится к нормальному;

• математический аппарат анализа гауссовских процессов наи­более (или достаточно) прост; стационарный гауссовский процесс полностью описывается, если известны его математическое ожи­дание и корреляционная функция.

Нередко анализ удается провести только для гауссовских про­цессов.

Одномерная ПРВ гауссовского процесса описывается выраже­нием

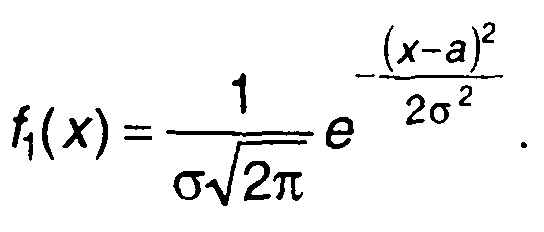(15.23)

Как следует из (15.23), одномерная ПРВ определяется двумя параметрами: а и σ. Параметр а представляет математическое ожидание случайного процесса

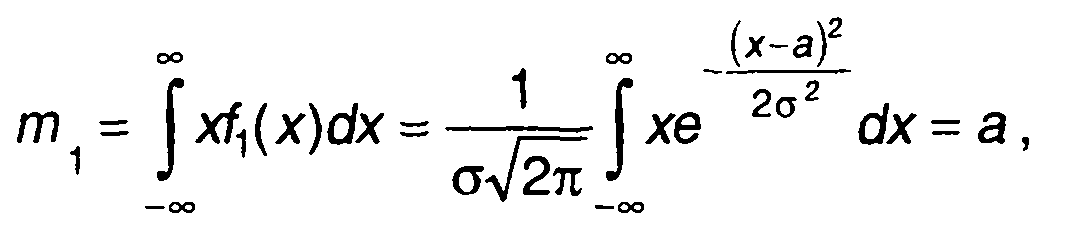(15.24)

σ² является дисперсией

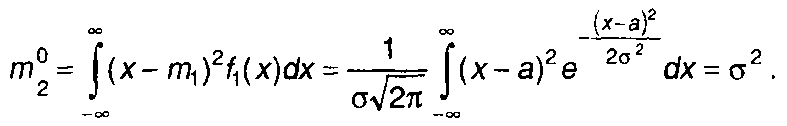(15.25)

Кривая ПРВ гауссовского процесса приведена на рис. 15.5,а. Она симметрична относительно математического ожидания, имеет максимум при х = а

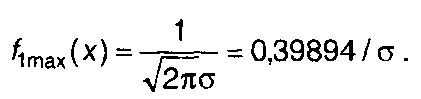
Максимальная крутизна кривой (точка перегиба) при х = а±σ. ФРВ гауссовского процесса определяется как (рис. 15.5,б)

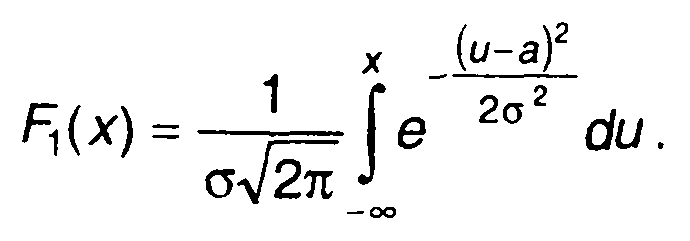(15.26)

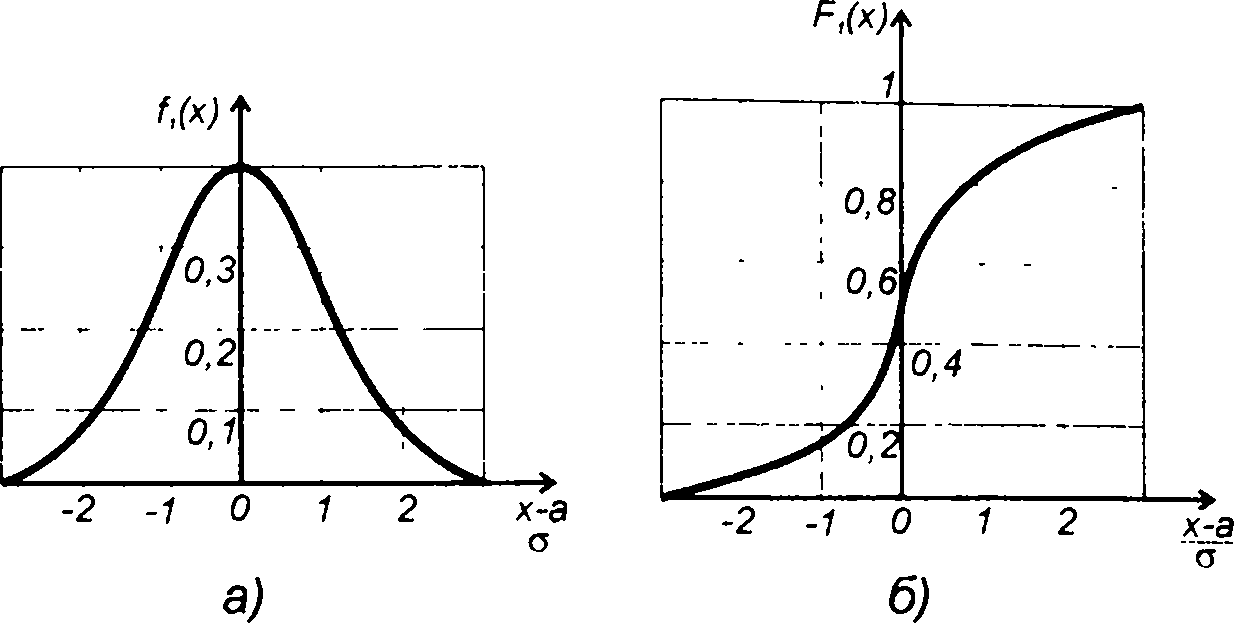
Рис. 15.5

Расчет ПРВ и ФРВ гауссовского процесса может производиться с использованием табулированных функций:

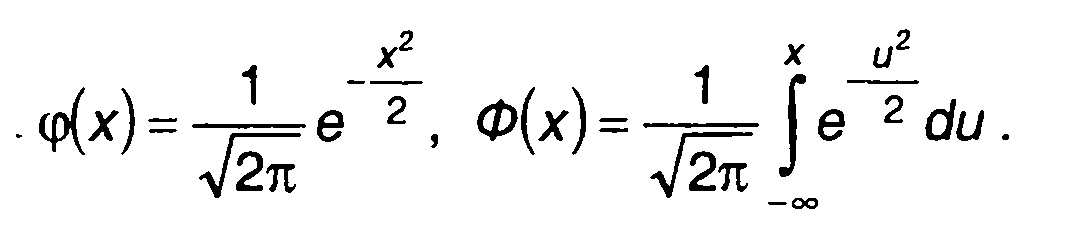(15.27)

При расчете ФРВ гауссовского процесса может также использо­ваться табулированная функция

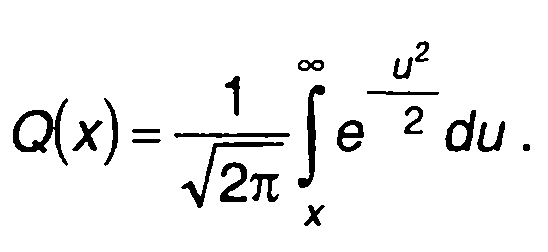(15.28)

Из сравнения (15.27) и (15.28) следует, что

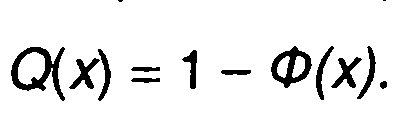
Составлены также таблицы интеграла вероятностей (функции ошибок)

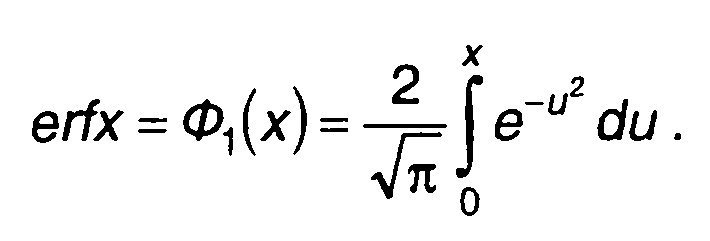(15.29)

Функция Ф₁(х) часто используется в решениях интегралов.

Для малых значений х функция Ф(х) может быть аппроксимиро­вана рядом

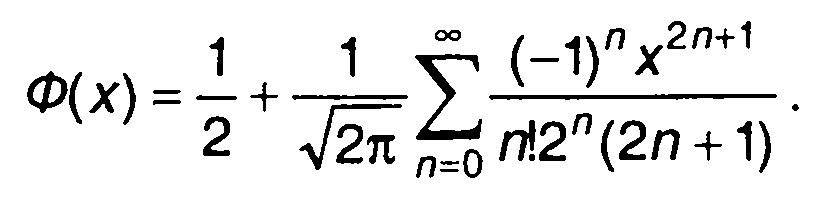
При достаточно большом значении аргумента полезна следую­щая аппроксимация:

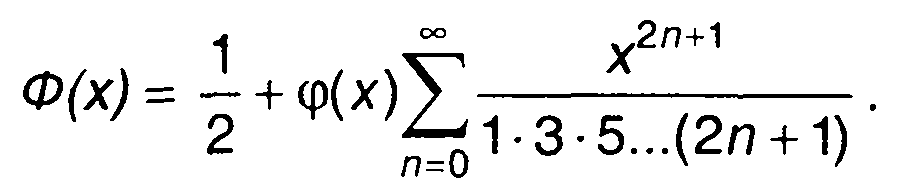
Из (15.13) с учетом (15.23) можно получить центральные момен­ты распределения гауссовского процесса

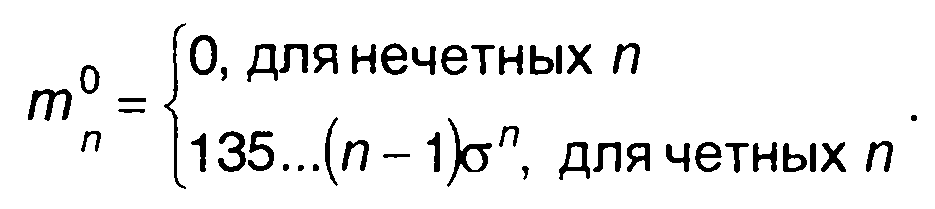(15.30)

2. Релеевский процесс

Преобразование гауссовского процесса может привести к случай­ному процессу, имеющему обобщенное распределение Релея. ПРВ такого случайного процесса описывается выражением (рис. 15.6,а)

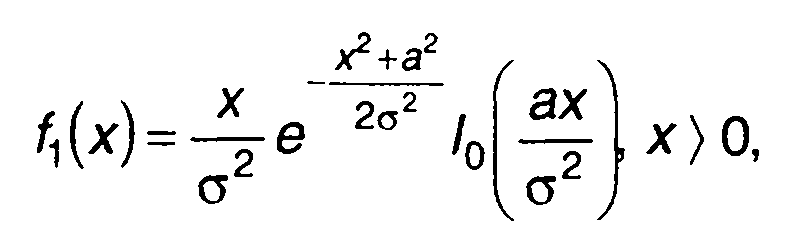(15.31)

где а, σ - параметры распределения; l₀(х) - модифицированная функция Бесселя первого рода:

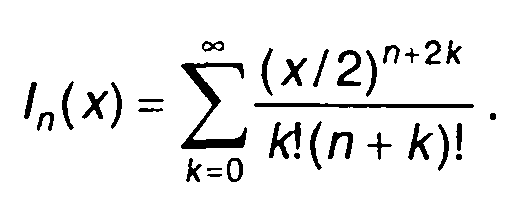
ФРВ релеевского процесса определяется как

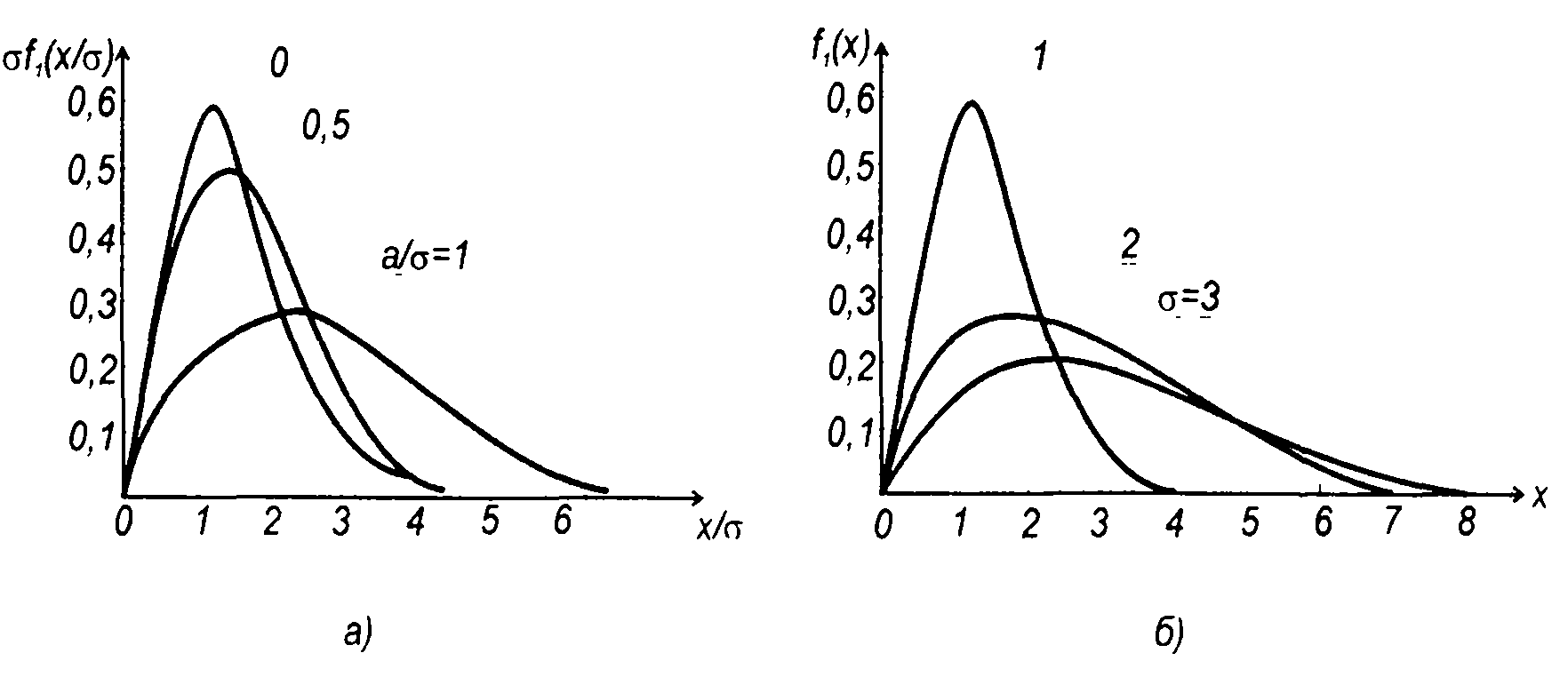
Рис. 15.6

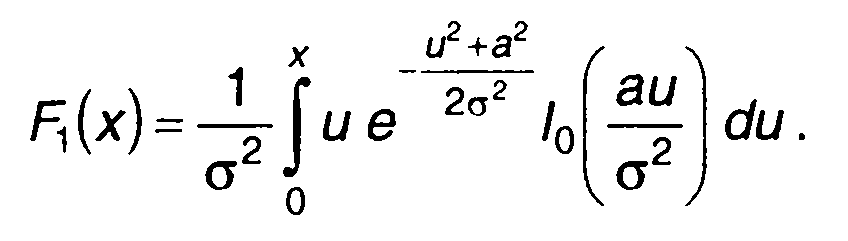(15.32)

Используя известное соотношение

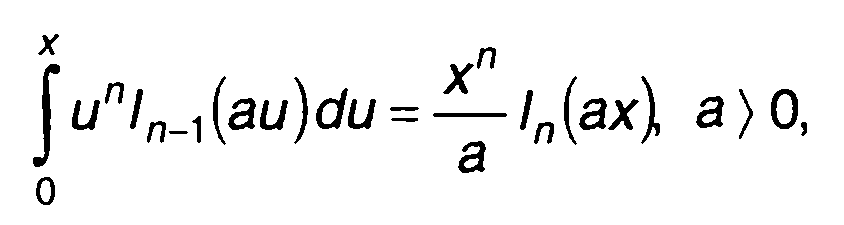(15.33)

выражение для ФРВ запишем в виде

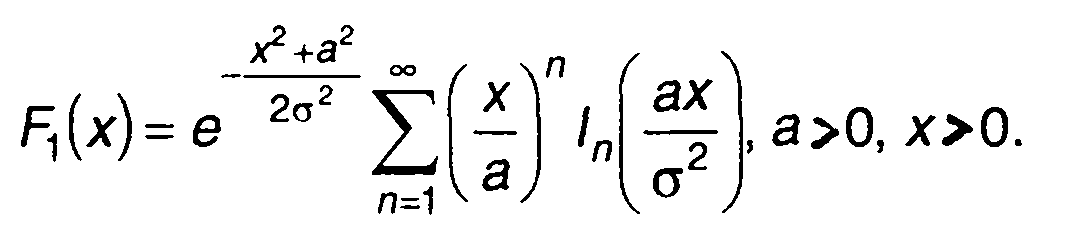(15.34)

При малых значениях отношения а/а, раскладывая функцию Бесселя в (15.31) в степенной ряд и ограничиваясь первыми двумя членами разложения, получим

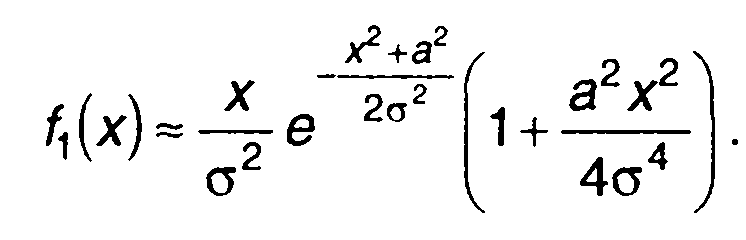(15.35)

При больших значениях а/о можно воспользоваться следую­щим разложением:

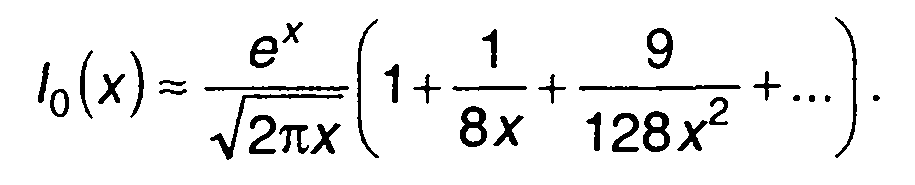(15.36)

Ограничиваясь первыми двумя членами разложения, выражение для ПРВ запишем в виде

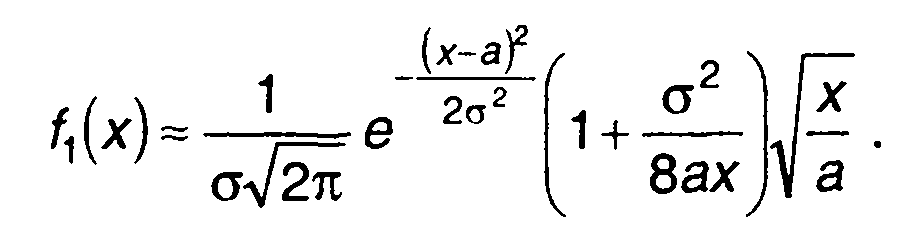(15.37)

При а/σ >> 1 обобщенный закон распределения Релея перехо­дит в нормальный с параметрами а и σ.

Моменты распределения вероятностей при обобщенном законе Релея определяются выражением

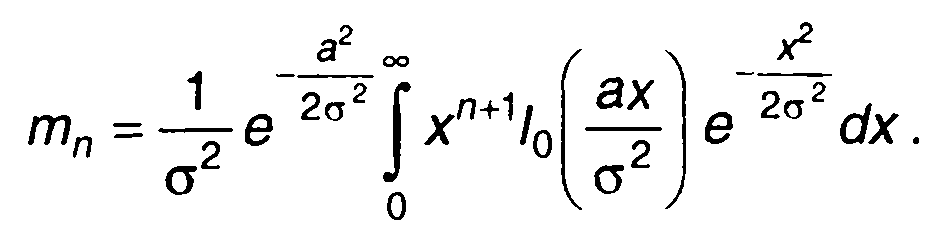(15.38)

Решение интеграла в (15.38) дает

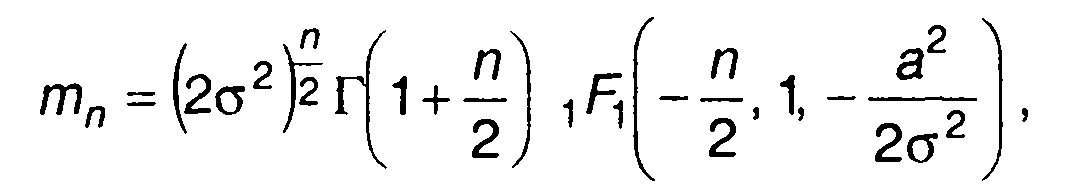(15.39)

где Г(х) - гамма-функция; ₁F₁(х₁, х₂,х₃)-вырожденная гипергеометрическая функция.

Если а = 0, то из (15.31) получим распределение Релея (рис. 15.6,6)

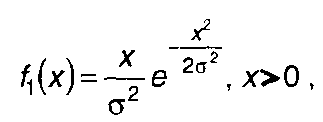(15.40)

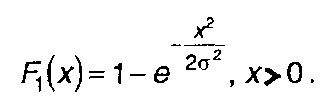(15.41)

Моменты распределения вероятностей релеевского случайного процесса определяются выражением

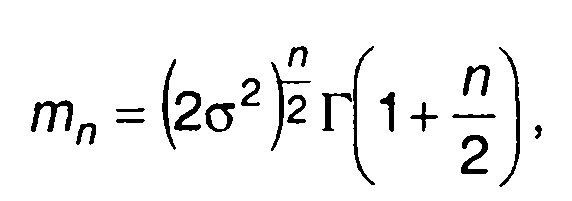(15.42)

среднее значение

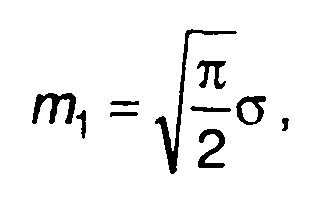
дисперсия

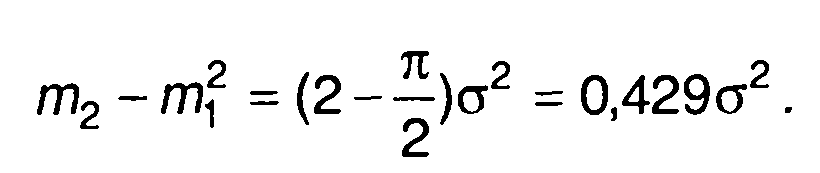
Некоторые наиболее известные виды распределений непрерыв­ных случайных величин приведены в табл. 15.1.

3. Телеграфный сигнал

Примером дискретного случайного процесса может служить слу­чайный процесс, реализация которого изображена на рис. 15.7,а. Случайный процесс принимает только два значения A₁, и A₂ а моменты перемены значений случайны. Такой случайный процесс получается, например, на выходе идеального ограничителя при по­даче на вход непрерывного случайного процесса . Его ФРВ равна

Таблица 15.1.

Характеристики распределения вероятностей случайных величин

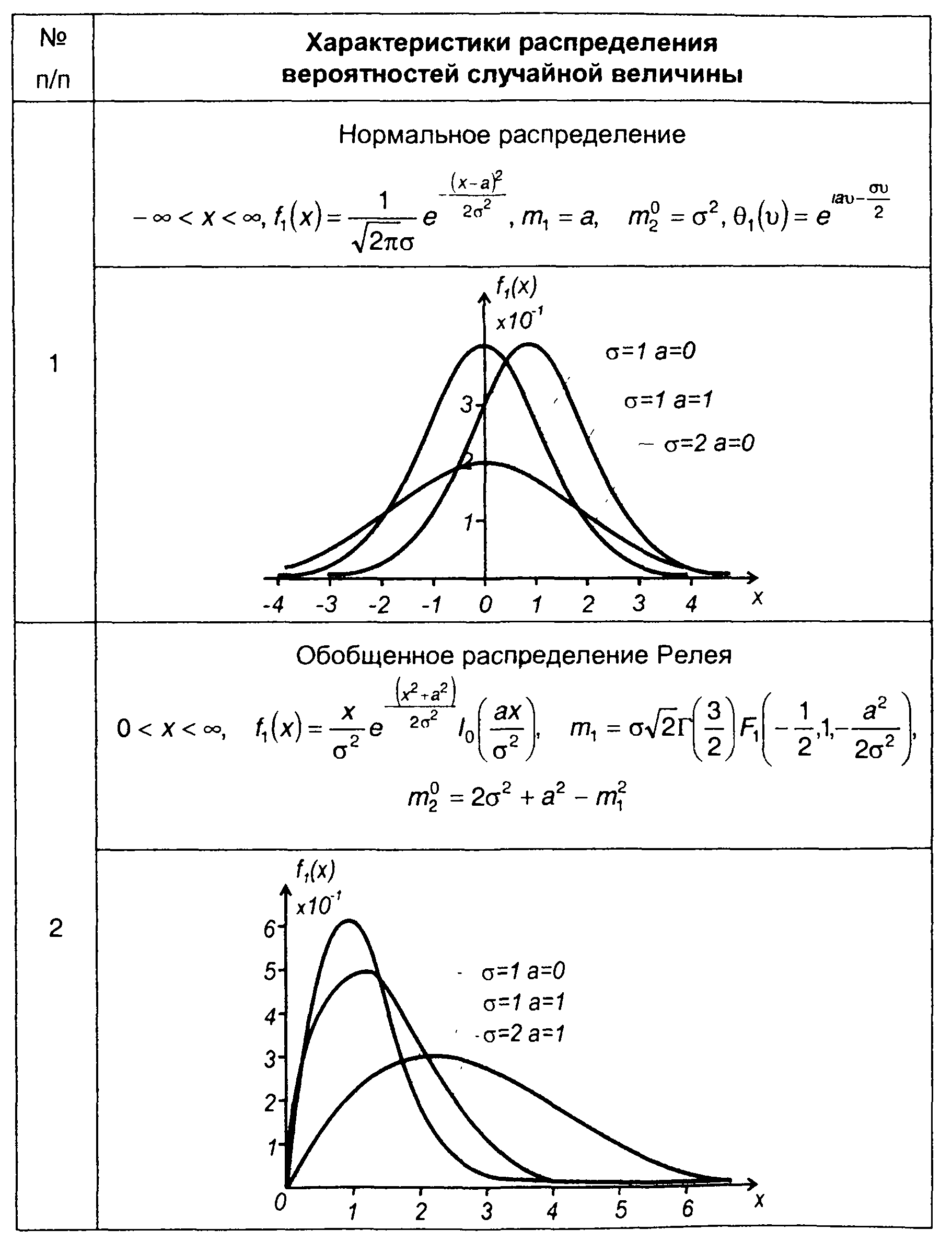
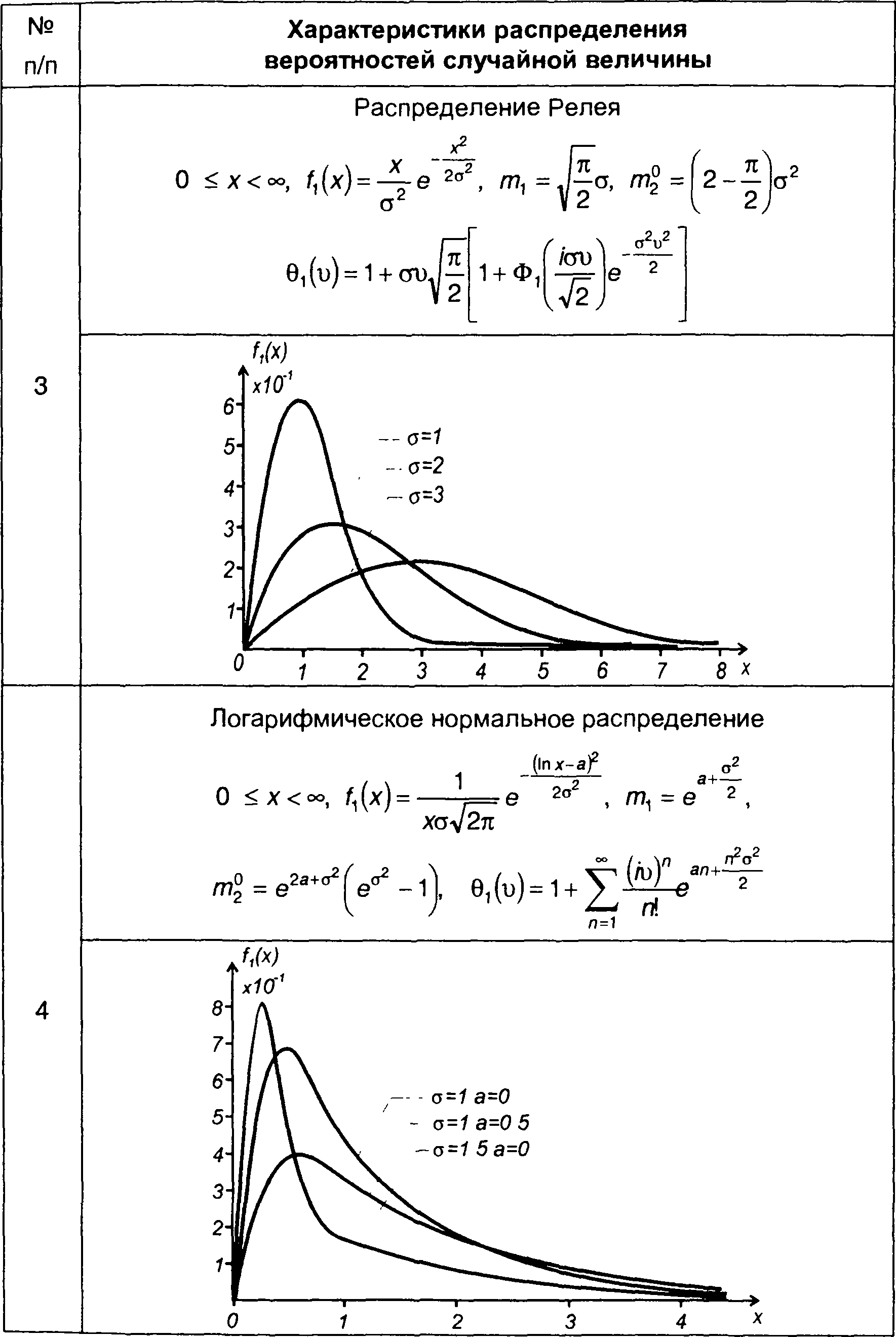
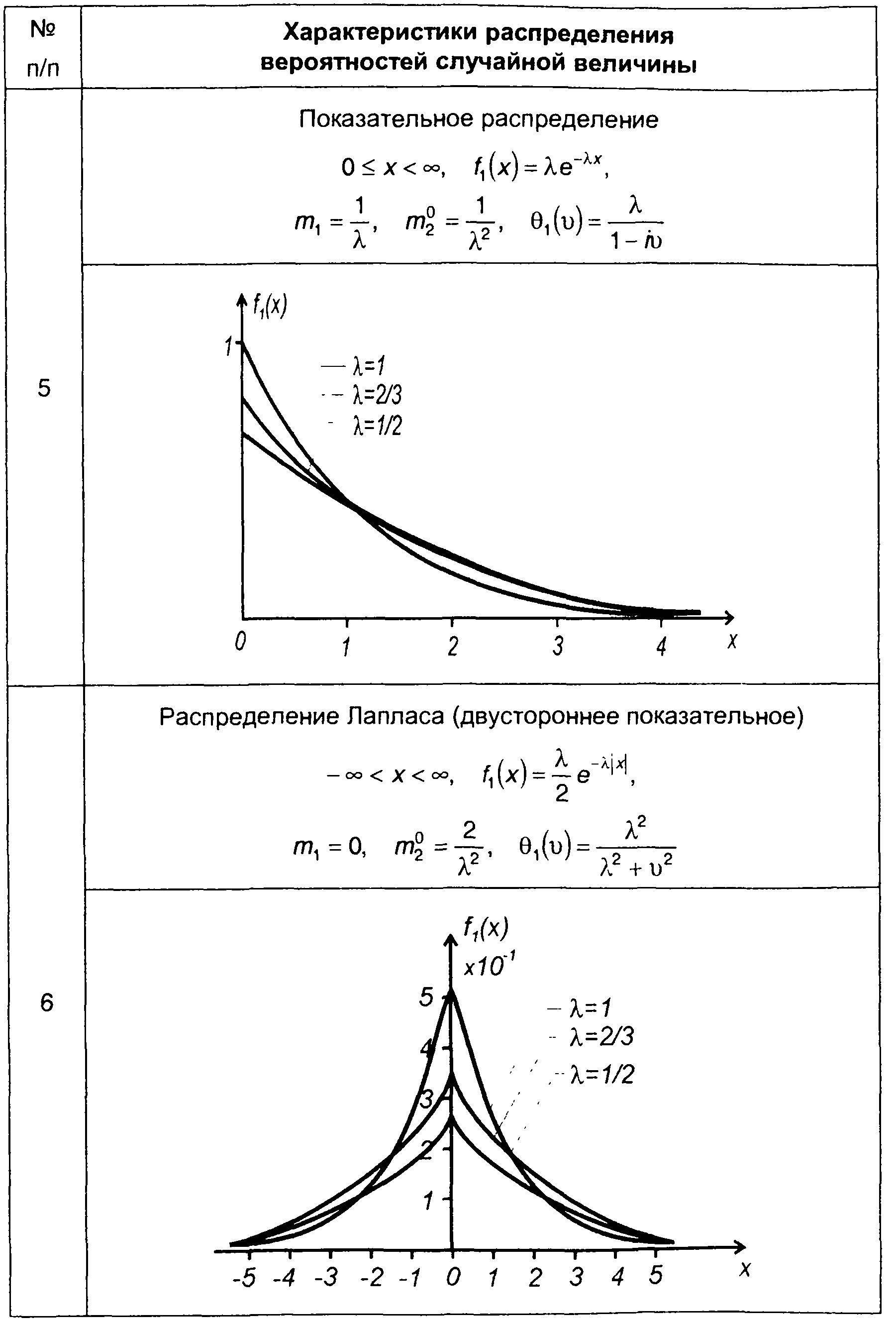
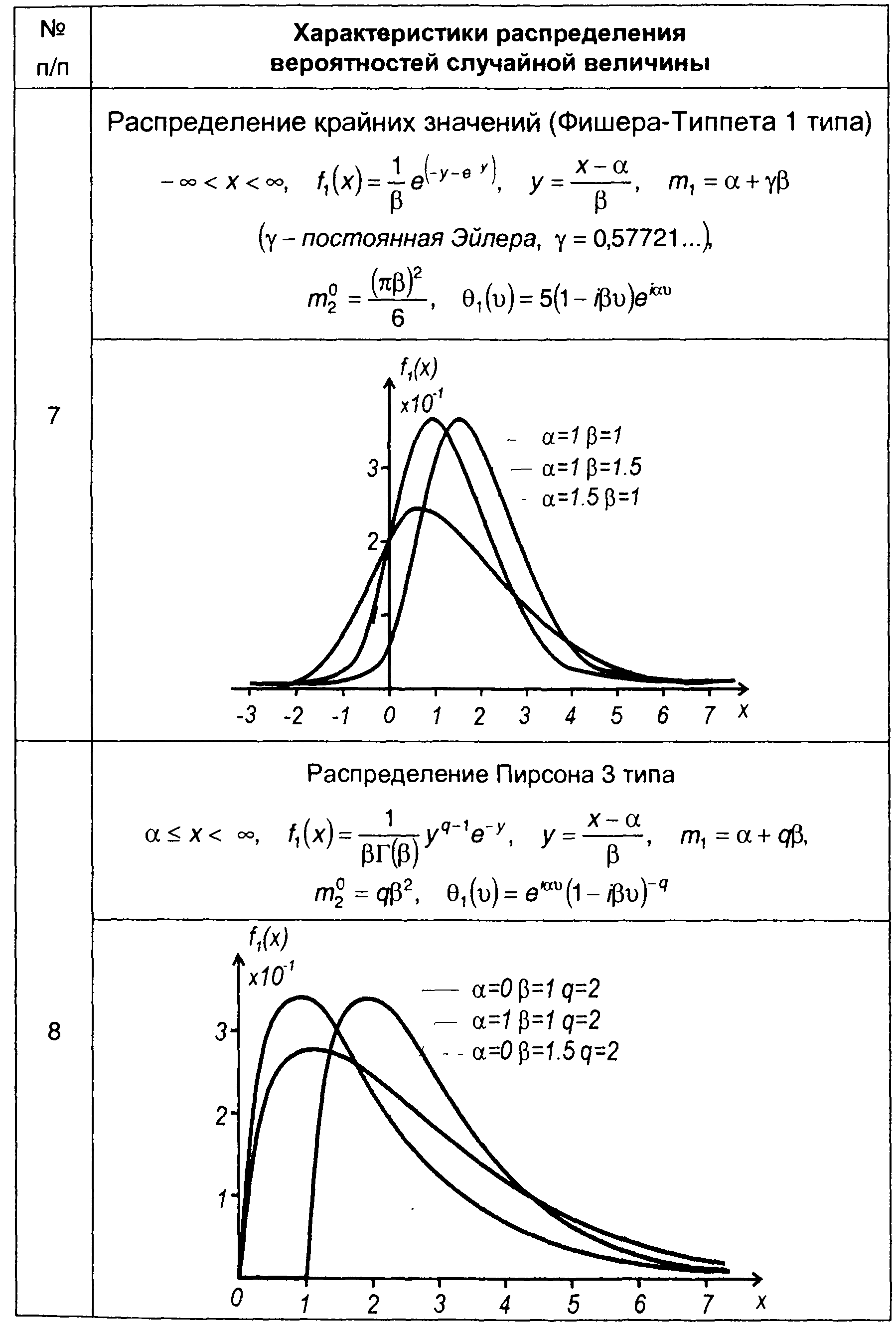
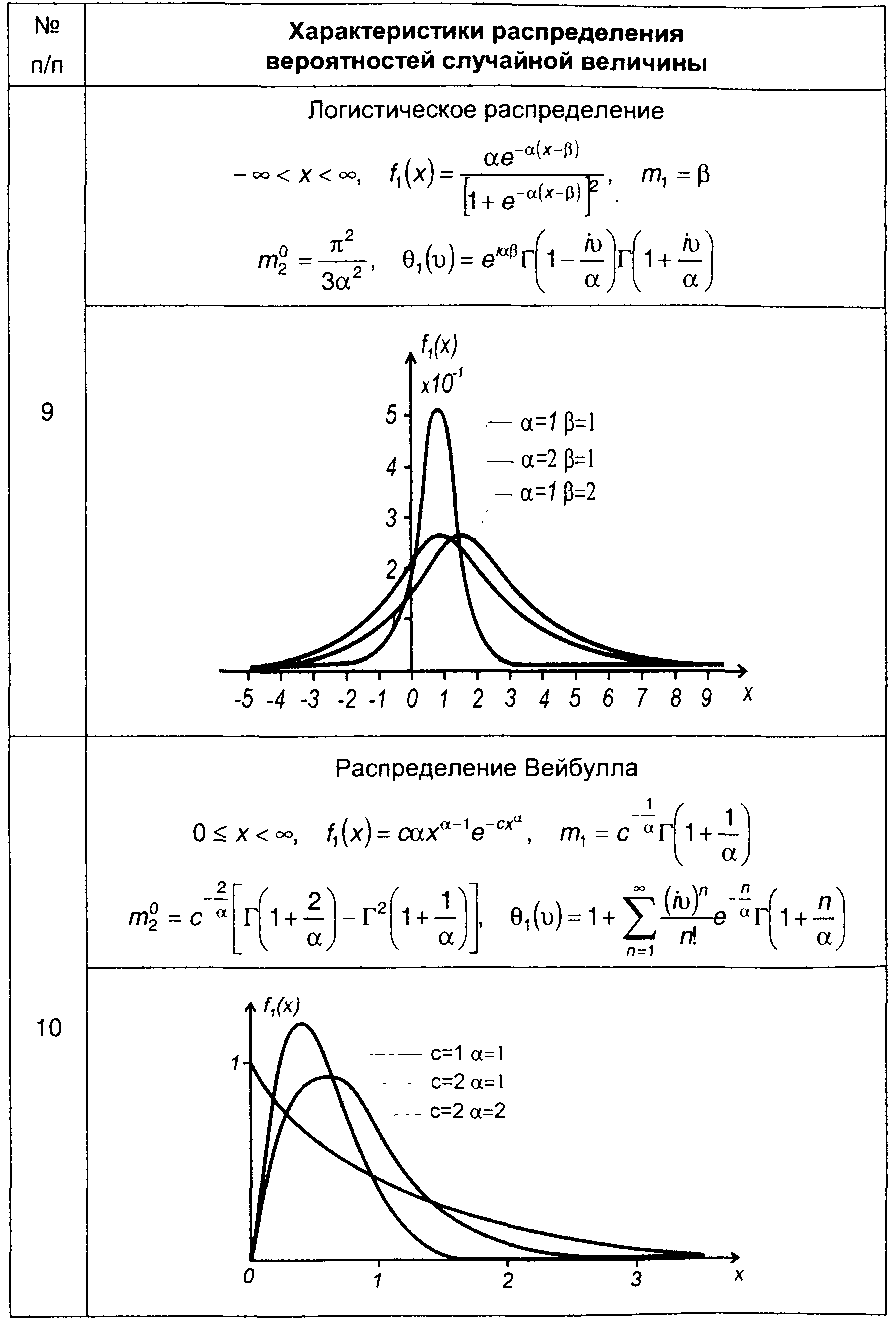
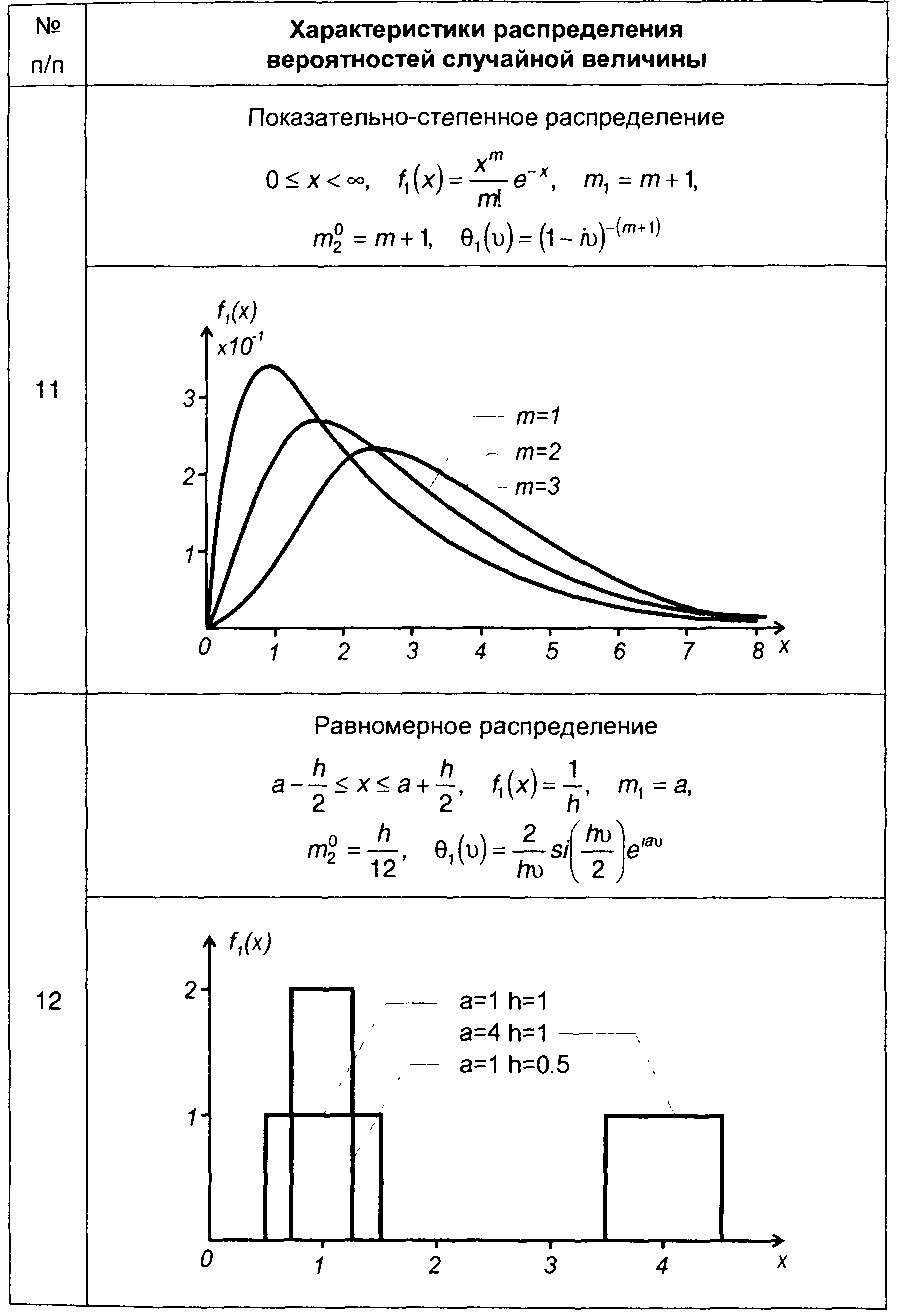
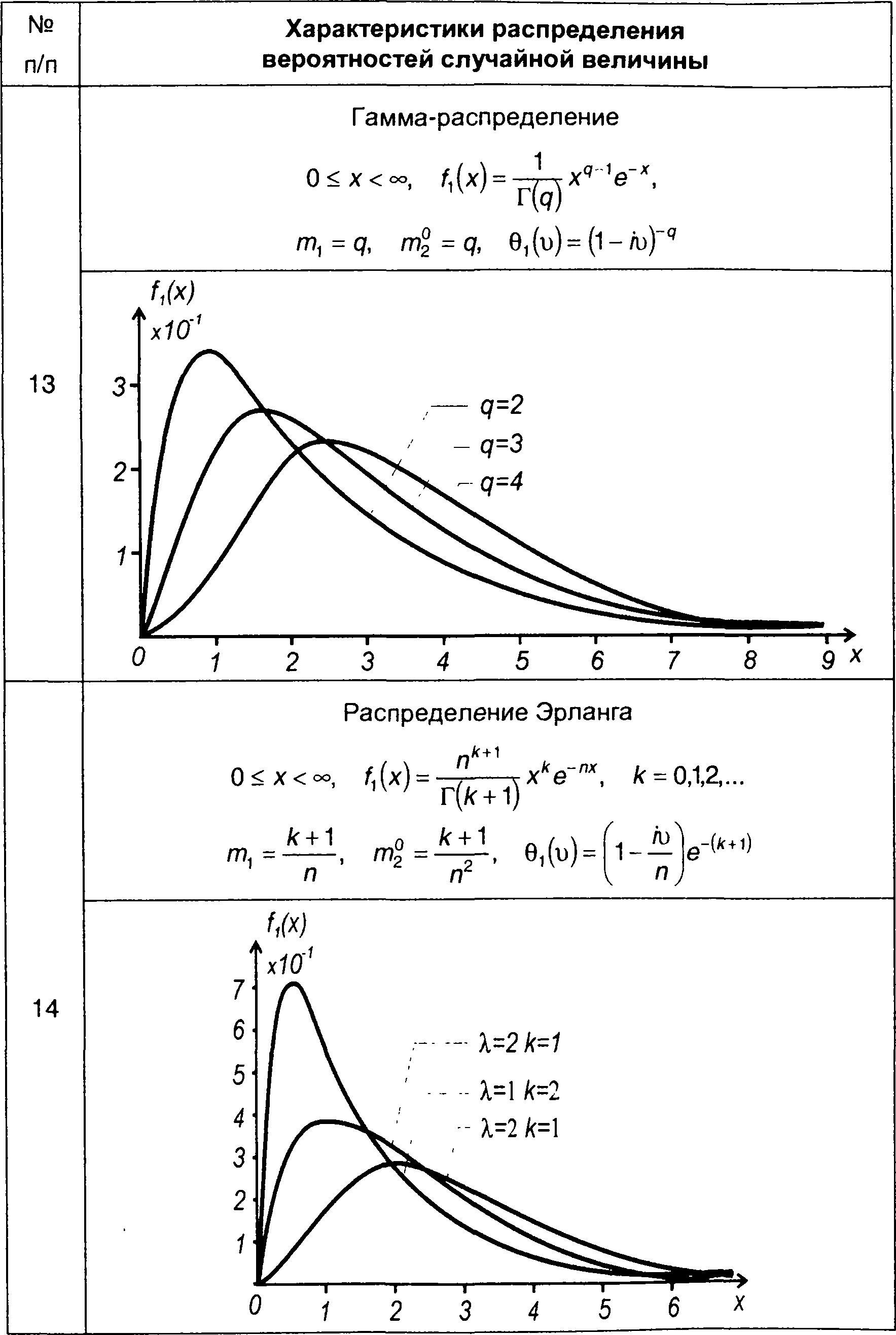
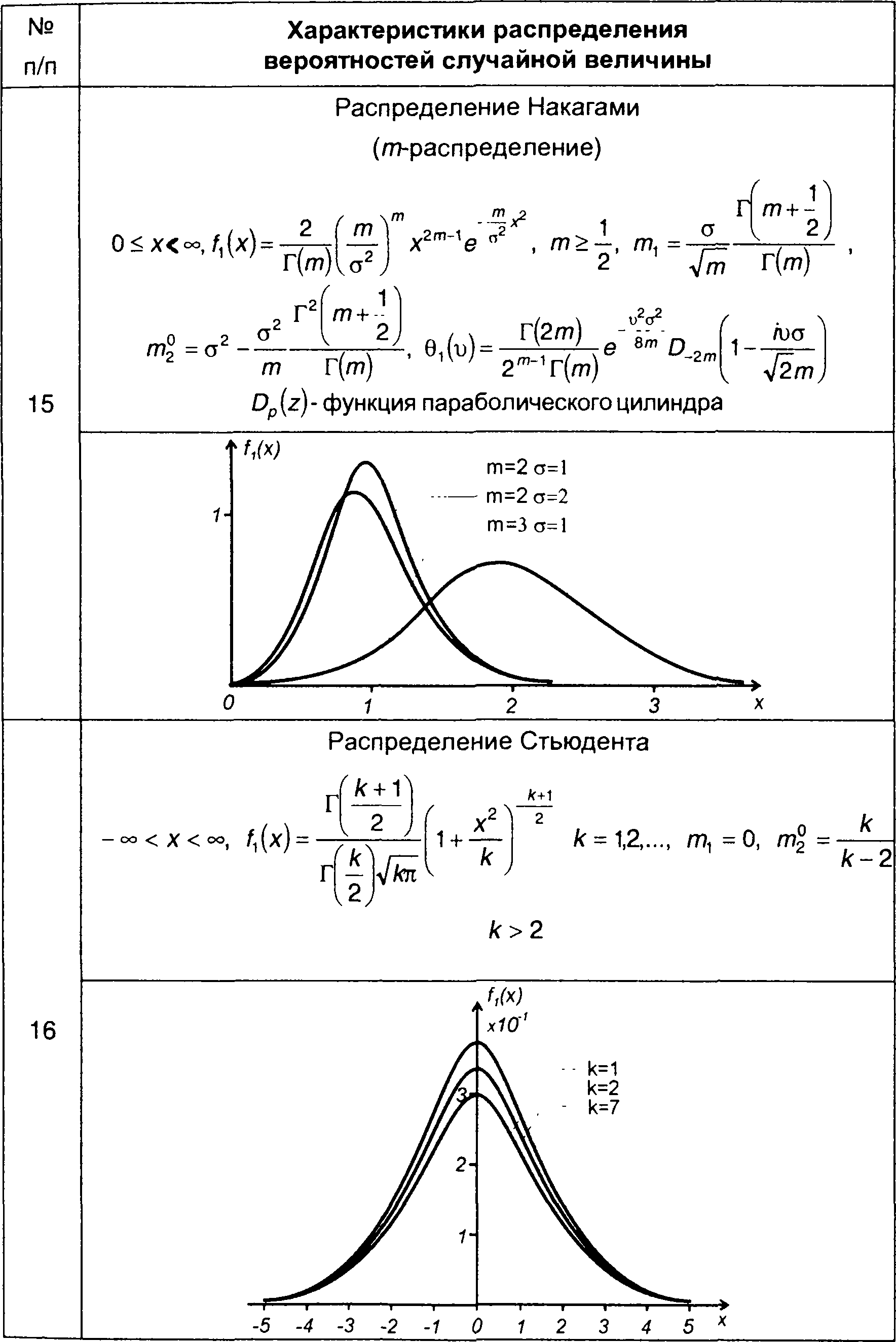
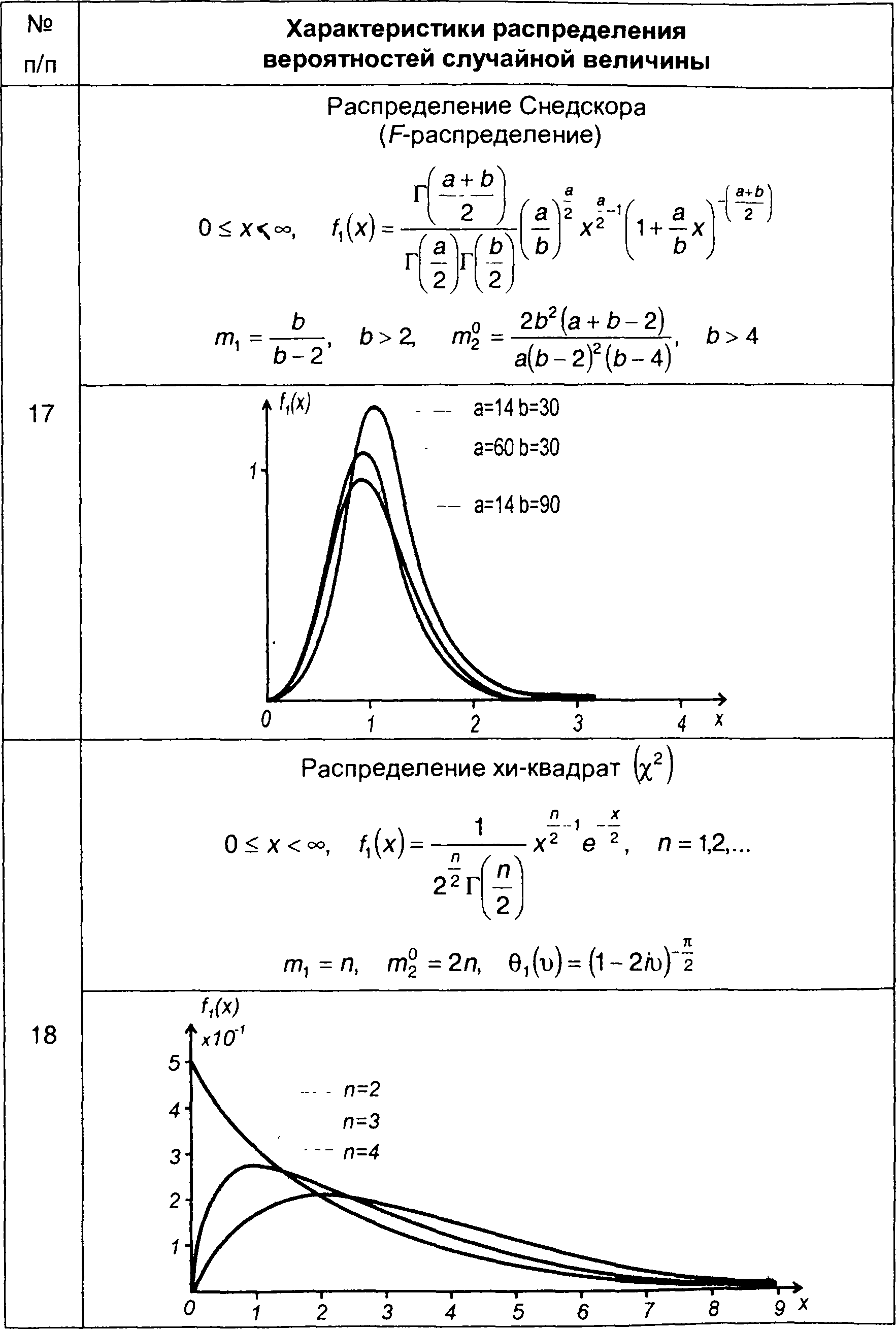
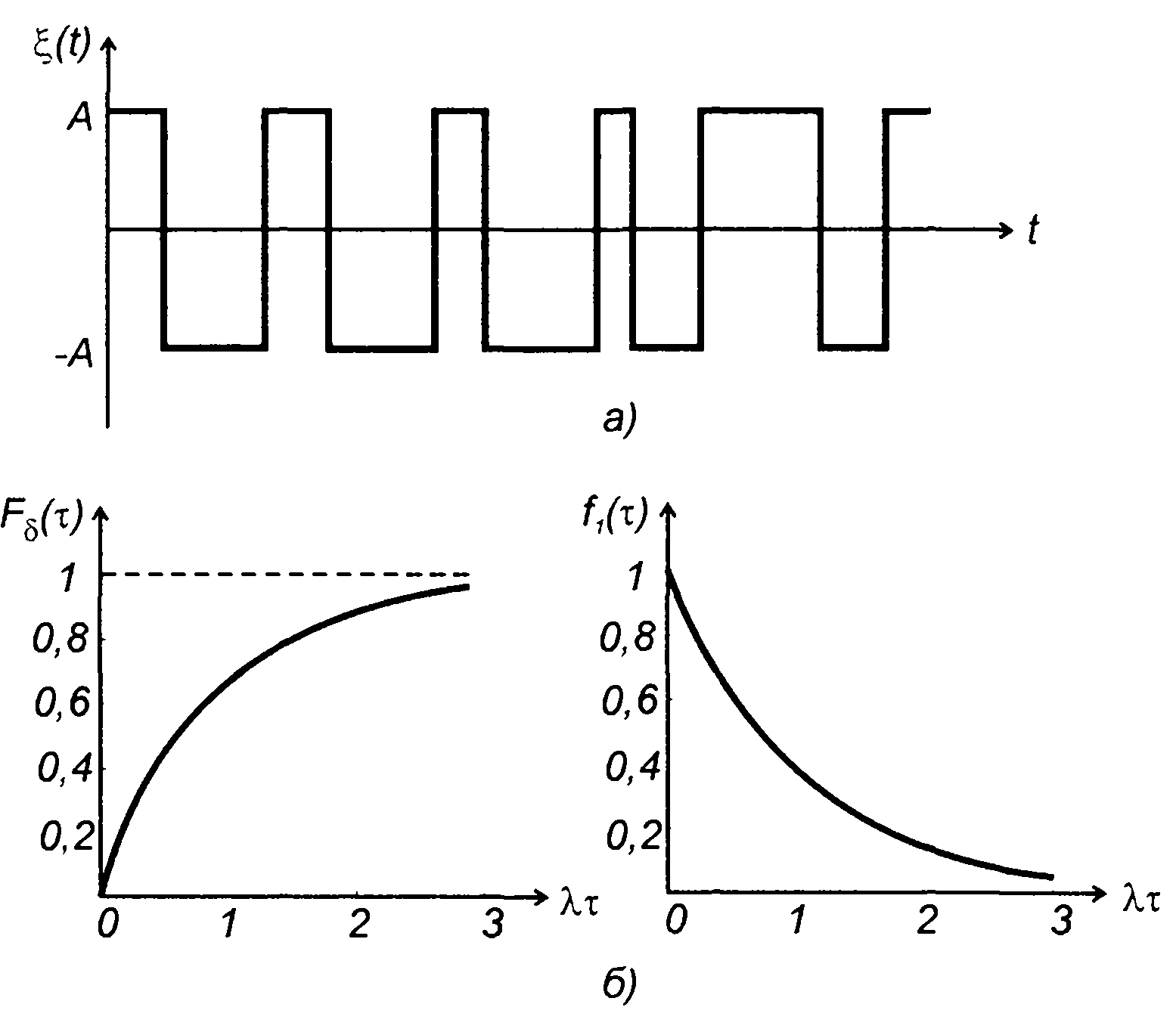
Рис. 15.7

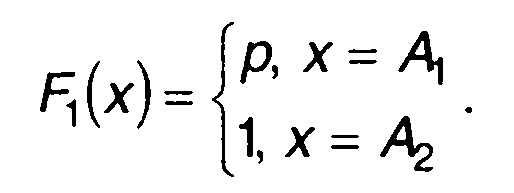(15.43)

ПРВ случайного процесса описывается с помощью импульсных функций

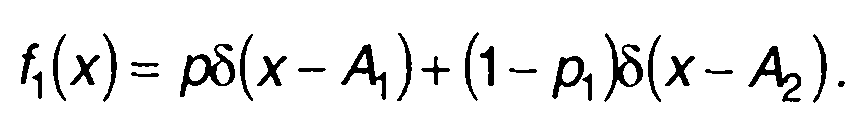(15.44)

Начальные моменты получаются из выражения

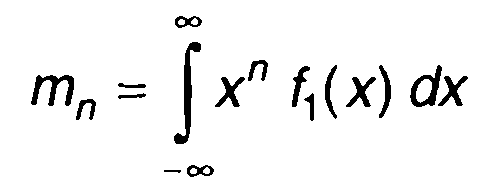
с подстановкой (15.44). Они равны

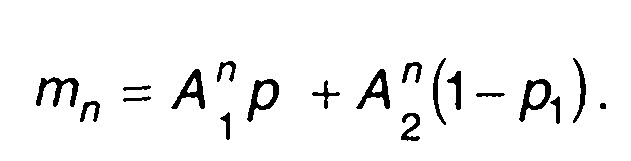(15.45)

Математическое ожидание

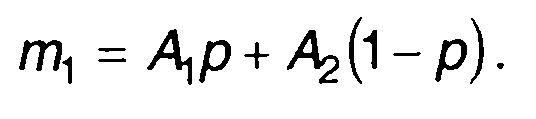(15.46)

Центральные моменты описываются выражением

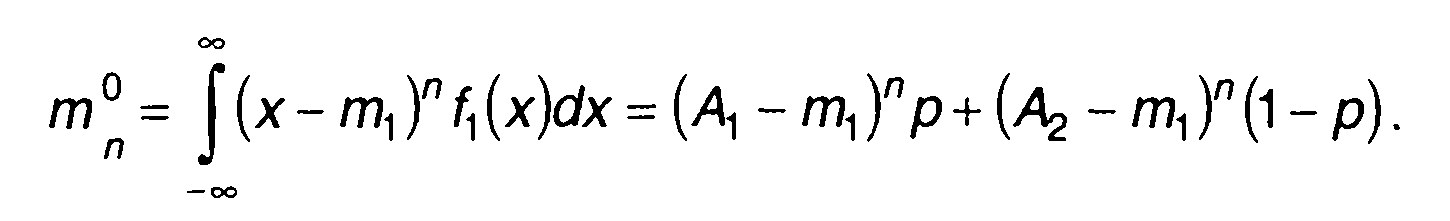(15.47)

Частным случаем рассматриваемого дискретного случайного процесса является телеграфный сигнал. Телеграфный сигнал представляет случайный процесс, принимающий значения: -А и А, моменты перемены знака подчиняются закону Пуассона