ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 4 страница

Таблица 3.2.

Спектральные плотности неинтегрируемых функций

3.5. Свойства преобразования Фурье и их использование при анализе сигналов

3.5.1. Свойства преобразования Фурье

При анализе сигналов полезно учитывать свойства преобразо­вания Фурье. Основные из них следующие.

1. Аддитивность.

Спектр суммы сигналов равен сумме спектров сигналов, т.е.

где <->- символ соответствия по Фурье,

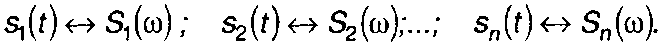
2. Смещение во времени.

Сигнал при смещении на время t₀ определяется выражением

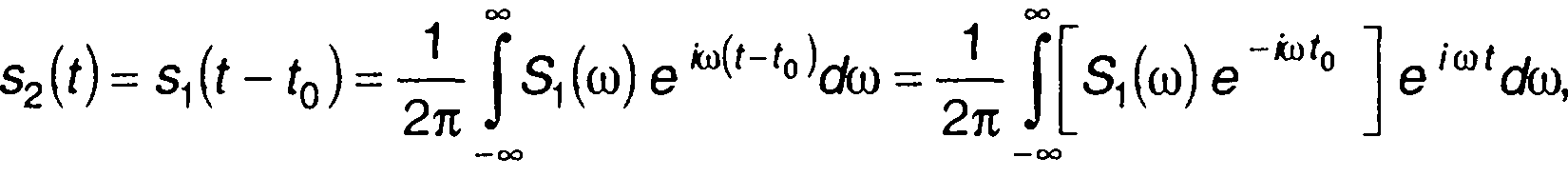
где t₀- смещение сигнала во времени. Таким образом,

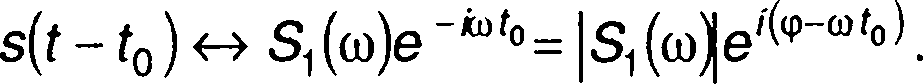(3.61)

Как следует из записанных выражений, спектр сигнала, запаз­дывающего на время t₀, равен произведению спектра исходного сигнала и множителя запаздывания е^_iωt0. Амплитудный спектр такого сигнала равен амплитудному спектру исходного сигнала, фа­зовый спектр - сумме фазового спектра исходного сигнала и ли­нейной функции времени (рис. 3.13).

3. Изменение масштаба времени.

При сжатии (растяжении) сигнала во времени s₂(t) = s₁(kt) (рис. 3.15) спектр определяется выражением

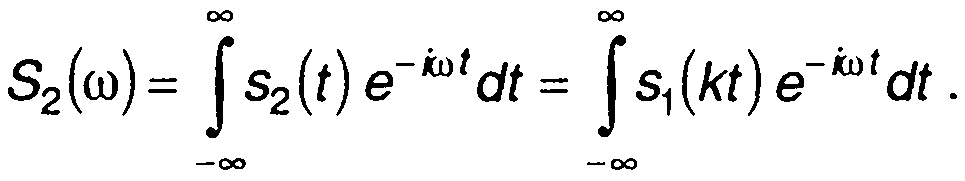
Переходя к новой переменной, получаем

Раздел 3

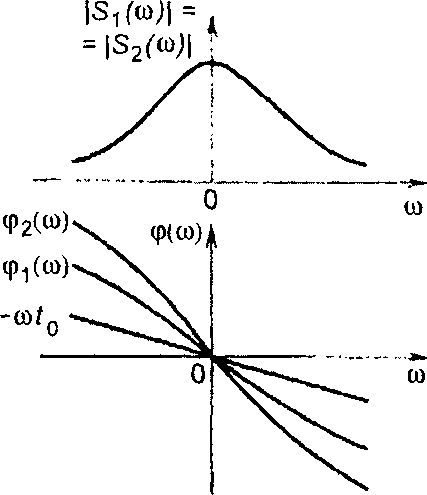
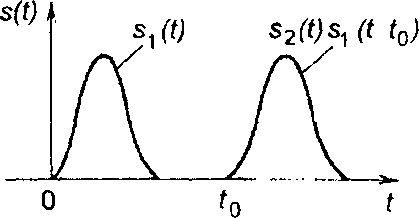
Рис. 3.13

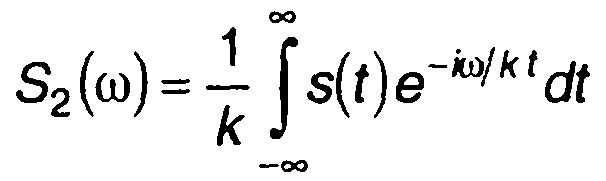
ИЛИ

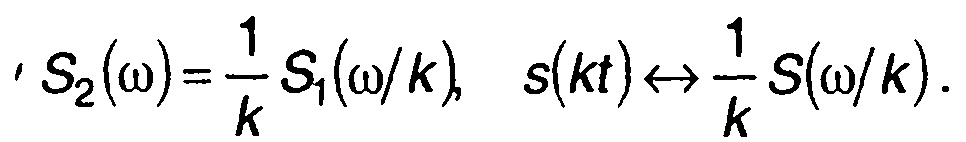(3.62)

Таким образом, сжатие (расширение) сигнала в k раз приводит к расширению (сжатию) его спектра в k раз (рис. 3.14).

4. Смещение спектра сигнала.

Если спектр сигнала смещен по частоте на величину ω, то

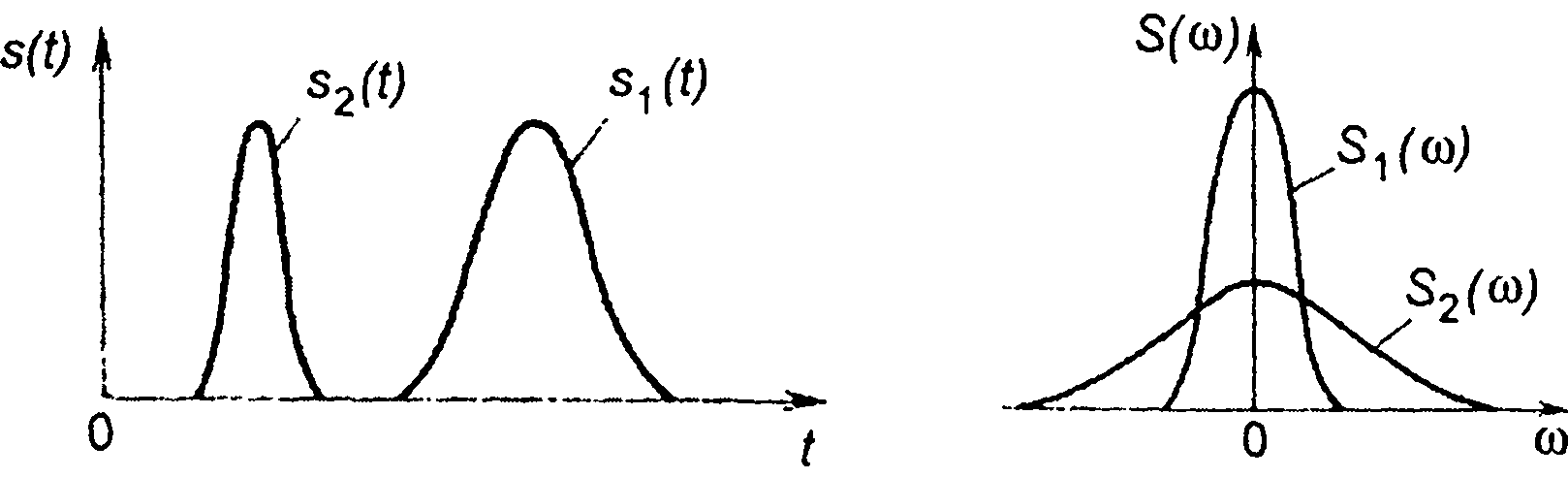
Рис. 3.14

Таким образом,

(3.63)

т.е. произведению сигнала на множитель фазового сдвига e^iω0t соответствует смещение всех составляющих спектра по частоте на величину ω₀.

5. Дифференцирование и интегрирование.

Для первой производной s(t) имеем

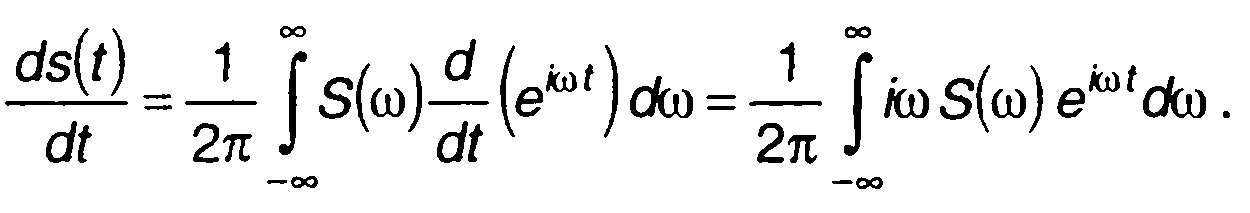
Для n -й производной получим

т.е. дифференцированию n раз сигнала по t соответствует умно­жение спектра на (iω)ⁿ

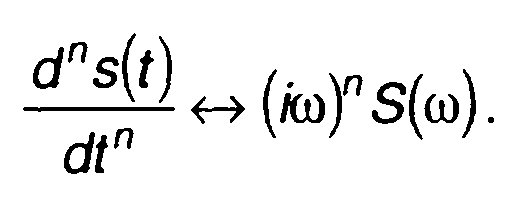(3.64)

Аналогично для интеграла от s(t)

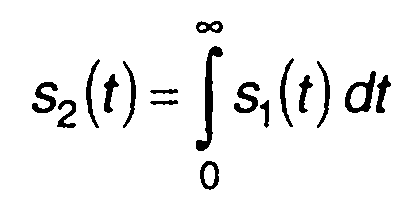
получим

(3.65)

6. Произведение двух сигналов.

Для сигнала, равного произведению двух сигналов

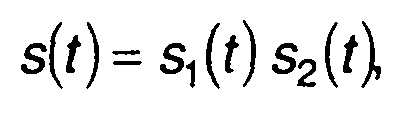
запишем

Подставляя в записанное выражение

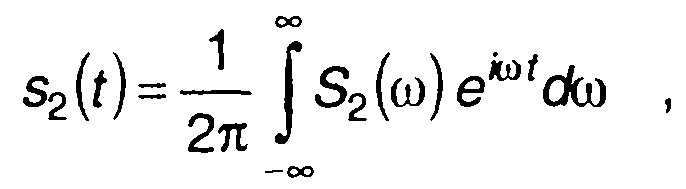
получаем

В полученном выражении имеем

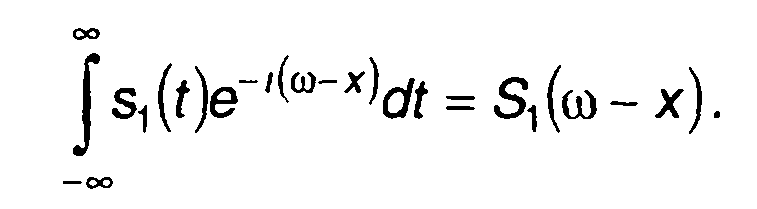
Спектральная плотность произведения двух сигналов определя­ется как

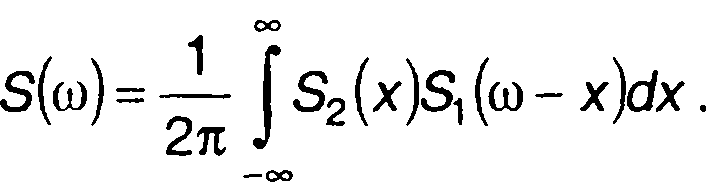
Таким образом,

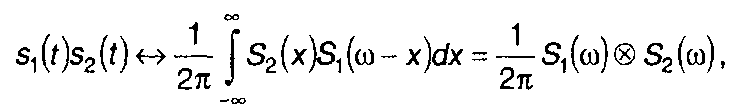(3.66)

где символ свертки; спектр произведения двух сигналов равен свертке их спектров с коэффициентом 1/2π;

Аналогично можно показать, что произведение двух спектров S₁(ω)S₂(ω) соответствует свертке функций s₁(t) и S₂(t)

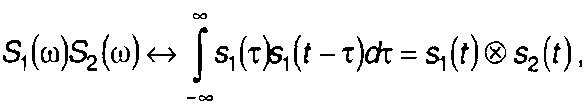(3.67)

7. Корреляционная функция сигналов.

Для интеграла

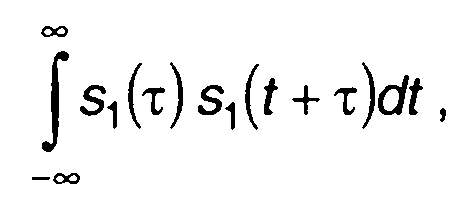
где τ - смещение во времени, по аналогии с (3.66) получим S₁(ω) S₂(ω).

Таким образом,

(3.68)

Для s₁(t) = s₂{t) = s(t) имеем

(3.69)

Величина |S(ω)|² = W(ω) представляет спектральную плотность энергии сигнала. Таким образом, корреляционной функции сигнала соответствует спектральная плотность энергии.

При т = 0

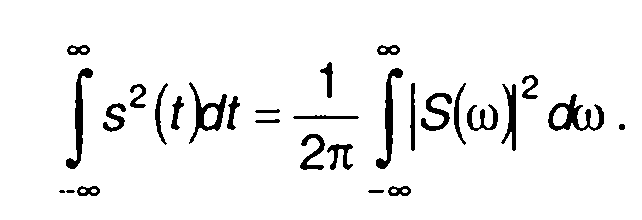(3.70)

Выражение (3.70) представляет равенство Парсеваля. Каждая часть равенства описывает энергию сигнала.

Основные свойства преобразования Фурье отражены в табл. 3.3.

Таблица 3.3.

Свойства преобразования Фурье

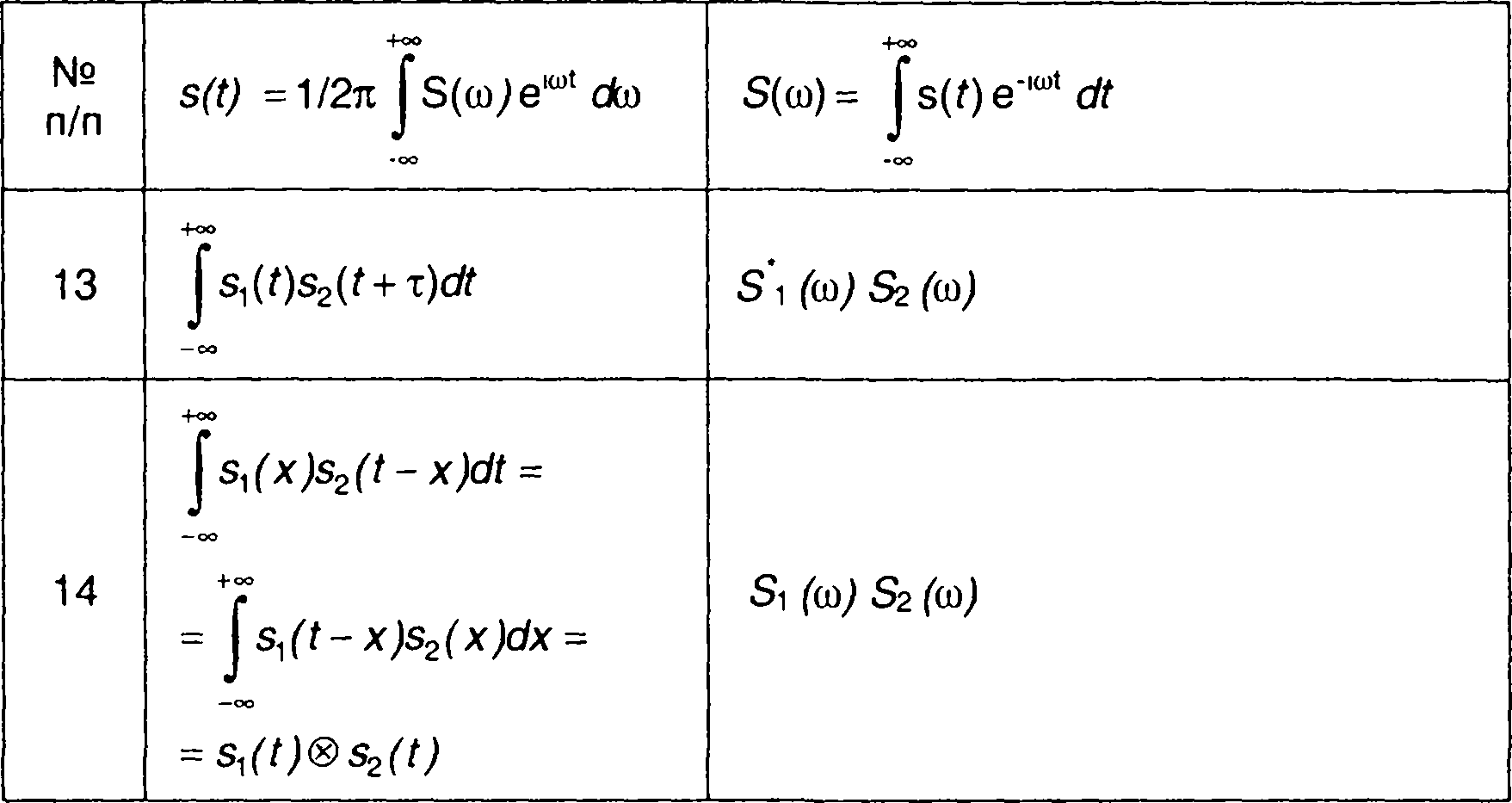
3.5.2. Примеры использования свойств преобразования Фурье при определении спектров сигналов

1. Сигнал, изображенный на рис. 3.15.

Спектральная плотность прямоугольного импульса единичной амплитуды, симметричного относительно начала координат, опи­сывается выражением

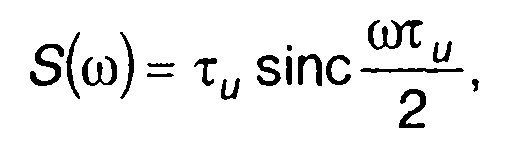
где τ_и - длительность импульса.

Сигнал можно рассматривать как совокупность (сумму) двух прямоугольных импульсов. Используя свойство 1, запишем

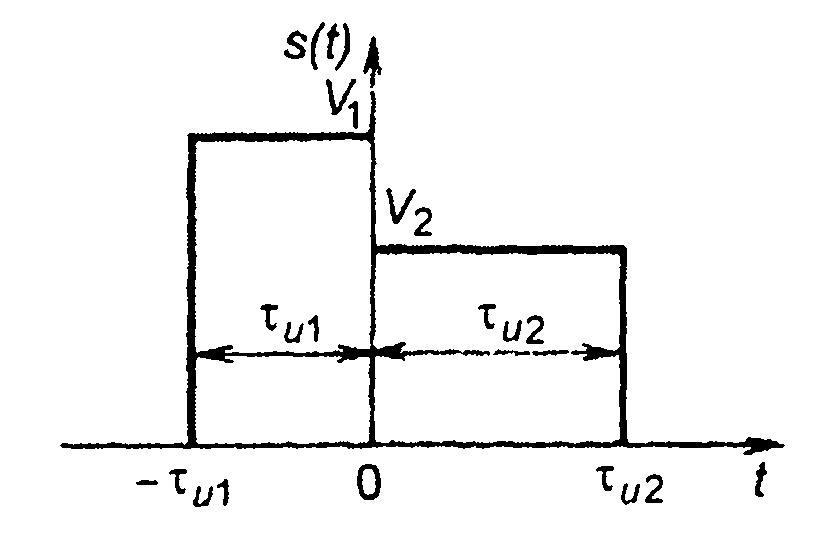
Рис.3.15

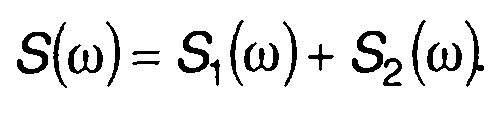
С учетом свойства 2 и решения примера 1 п. 3.2 получим

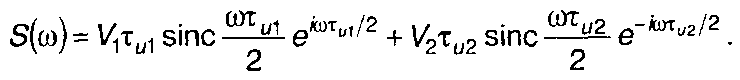
Амплитудный и фазовый спектры определяются выражениями

где

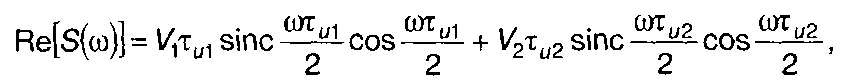
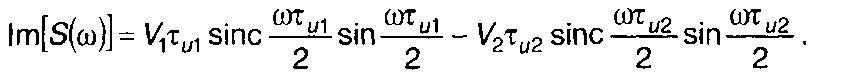
2. Периодический сигнал.

Используя выражение для спектральной плотности гармониче­ского сигнала, определяем спектральную плотность периодического сигнала. Периодический сигнал s(t) представим в виде ряда Фурье

(3.71)

где ω₁, - частота сигнала.

Преобразование Фурье (3.71) дает

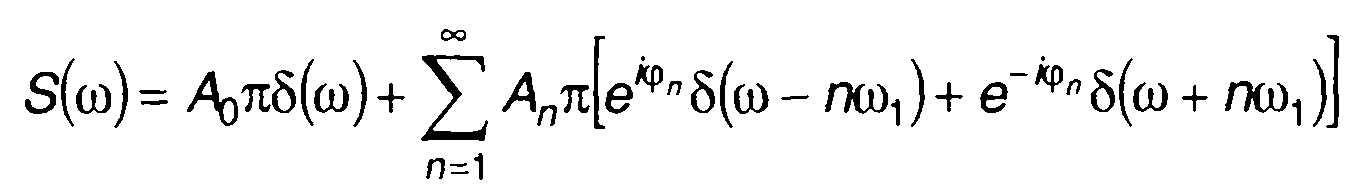(3.72)

или

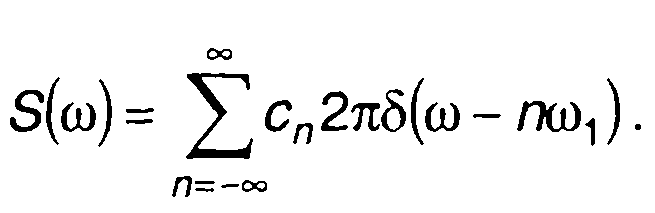(3.73)

Таким образом, спектральная плотность периодического сигнала представляет бесконечную сумму импульсных функций, умножен­ных на соответствующие коэффициенты и расположенных на час­тотах, кратных частоте сигнала.

3. Произведение сигнала и гармонического колебания.

(3-74)

Преобразование Фурье левой и правой частей (3.74) с учетом п.8 табл. 3.3 дает

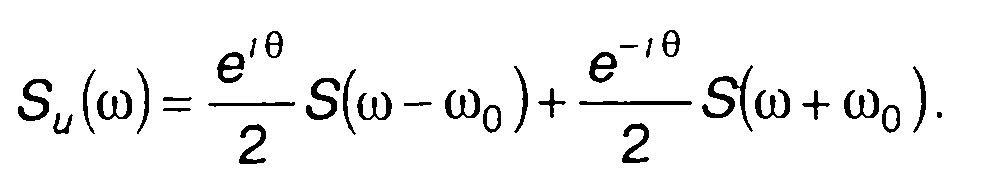(3.75)

При θ = 0 (рис. 3.16)

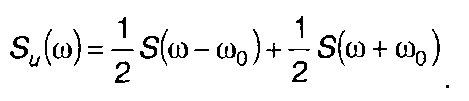(3.76)

Так, если s(t)= Ve^-at (рис. 3.17,а)

из (3.75) получим

Амплитудный спектр

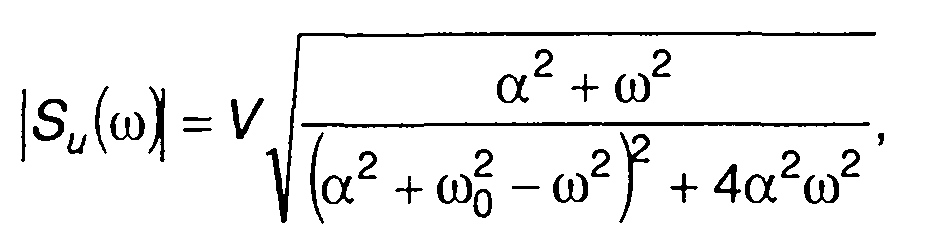
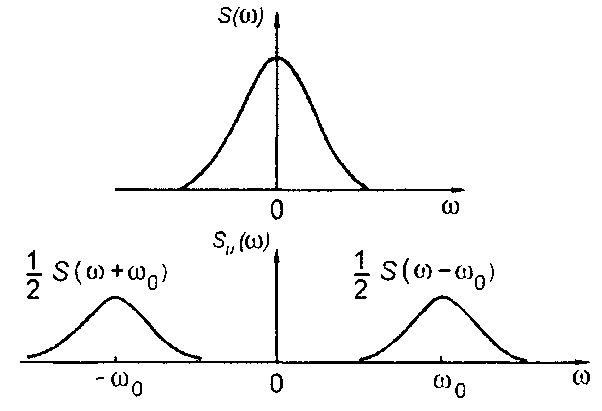
Рис. 3.16

Рис.3.17

фазовый спектр

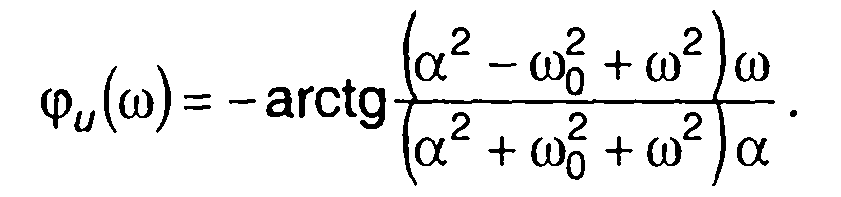
На рис. 3.17, б изображены амплитудные спектры сигнала при различных значениях ω₀.

4. Треугольный импульс.

При определении интеграла Фурье некоторых видов сигналов часто удобнее сначала произвести дифференцирование сигнала, найти преобразование Фурье производной, а затем перейти к пре­образованию Фурье исходного сигнала. Удобство такого приема связано с тем, что в результате дифференцирования некоторых видов сигналов появляется последовательность импульсных функ­ций, для которых известно преобразование Фурье. Метод приведе­ния к импульсным функциям поясним на примере определения спектра сигнала в виде треугольного импульса (рис. 3.18,а).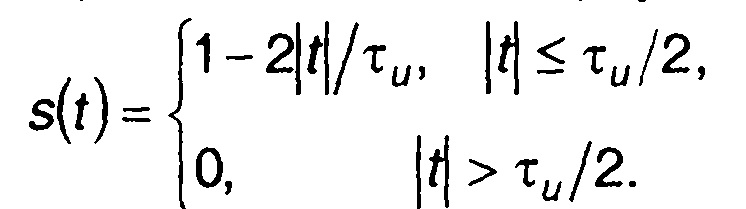

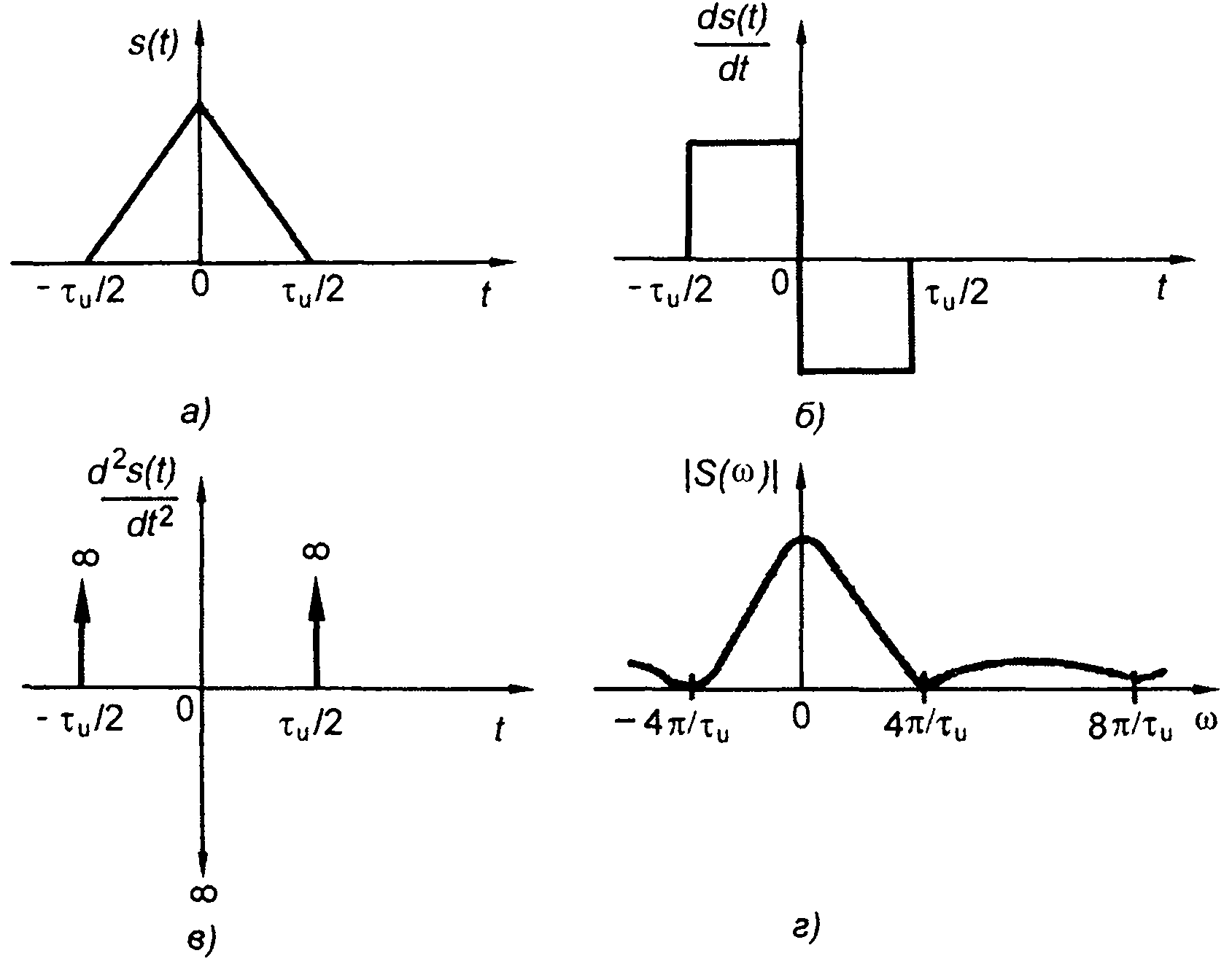
Рис. 3.18

Дважды продифференцировав функцию s(t), получим (рис. 3.18 б,в)

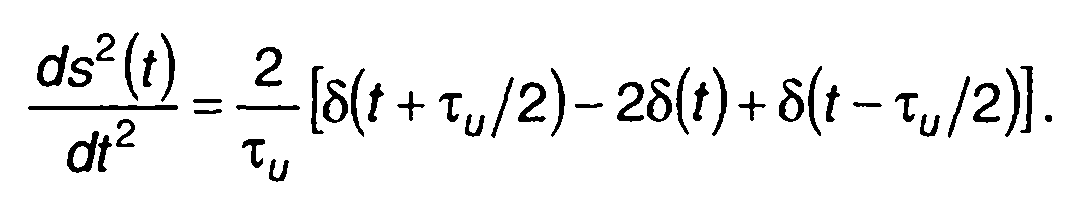
Преобразование Фурье левой и правой частей записанного вы­ражения дает

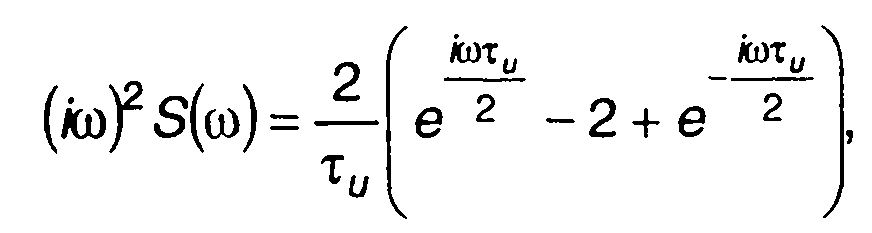
где S(ω) - спектральная плотность сигнала s(t).

После преобразования получим

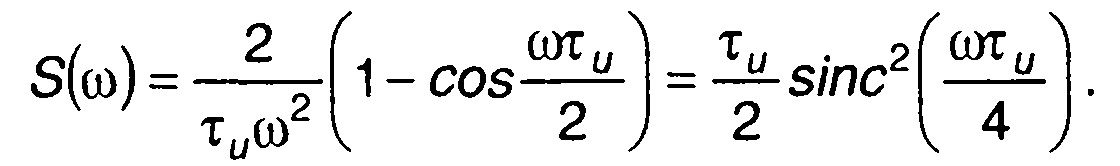
Амплитудный спектр сигнала показан на рис.3.18,г.

5. Пачки импульсов.

Пачки идентичных сигналов (импульсов) составляют достаточно обширный класс сигналов, встречающихся в инженерной практике. Поэтому спектральный анализ таких сигналов, помимо иллюстрации методического подхода, представляет самостоятельный интерес.

Спектральная плотность пачки импульсов определяется как сумма спектральных плотностей каждого из импульсов. При иден­тичной форме импульсов, обозначив спектральную плотность пер­вого импульса S₀(ω), для пачки импульсов запишем

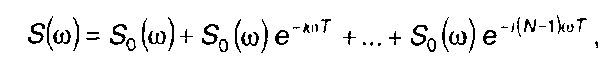(3.77)

где T- период следования импульсов в пачке; N- число импуль­сов в пачке.

В (3.77) множитель e^-iωT учитывает смещение во времени каждо­го последующего импульса по отношению к предыдущему. Из (3.77) с учетом формулы суммы геометрической прогрессии получим

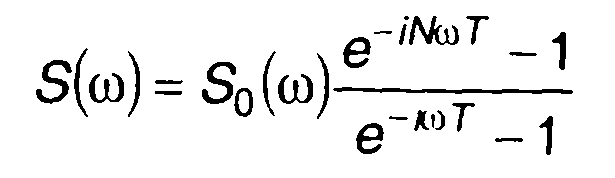
или после преобразования

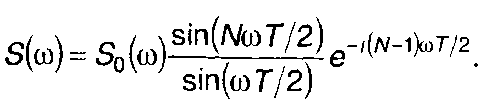(3.78)

При N → ∞

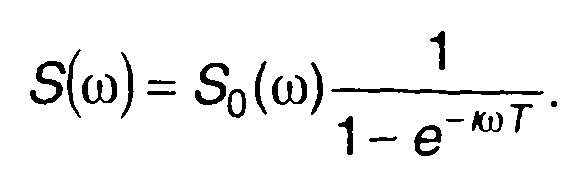(3.79)

С учетом (3.78) результаты, приведенные в табл. 3.1, можно ис­пользовать для определения спектров пачек различных импульсов.

1. Пачка прямоугольных импульсов (табл. 3.1, п.1), рис. 3.19.

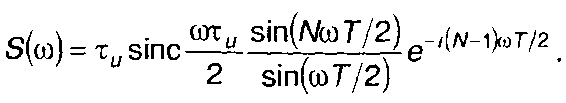
2. Пачка меандровых импульсов (табл. 3.1, п.2), рис. 3.20.

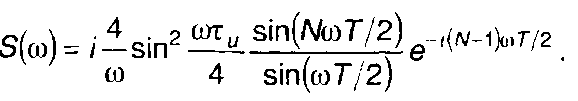
3. Пачка треугольных импульсов (табл. 3.1, п.З), рис. 3.21.

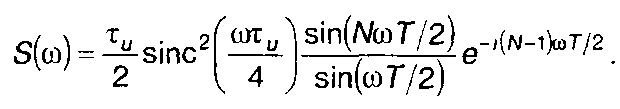
4. Пачка косинусоидальных импульсов (табл. 3.1, п.4), рис.3.22.

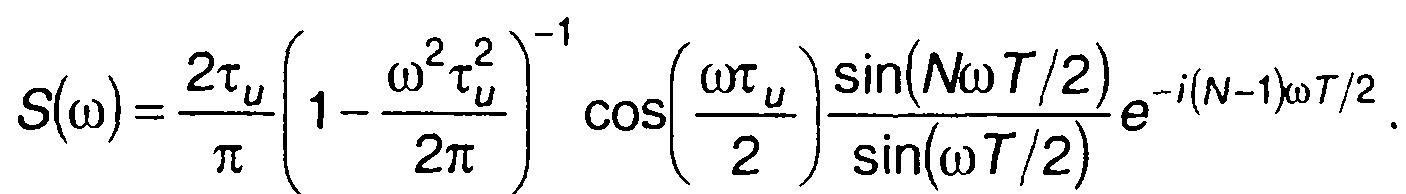
3.6. Спектральный анализ сигналов на основе преобразования Хартли

Преобразование Хартли является одним из интегральных пре­образований, которые могут найти применение при анализе сигна­лов, представляет модификацию преобразования Фурье. Отличи­тельная особенность преобразования Хартли состоит в том, что оно является действительным интегральным преобразованием.

Практически для всех сигналов, для которых существует преобразование Фурье, существует и преобразование Хартли.

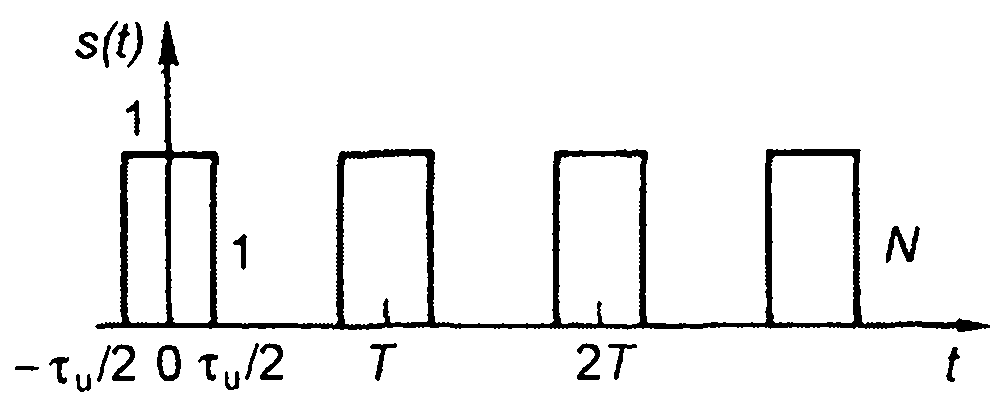
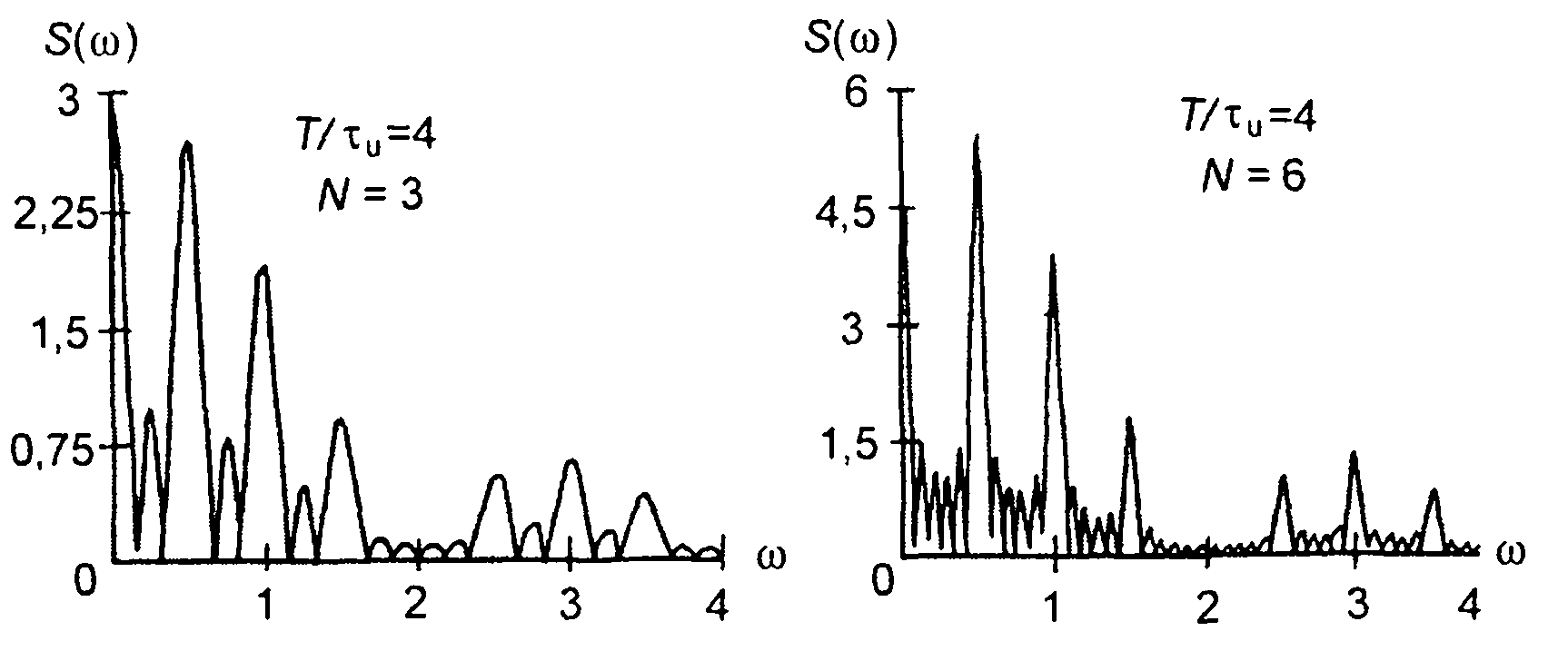
Рис. 3.19

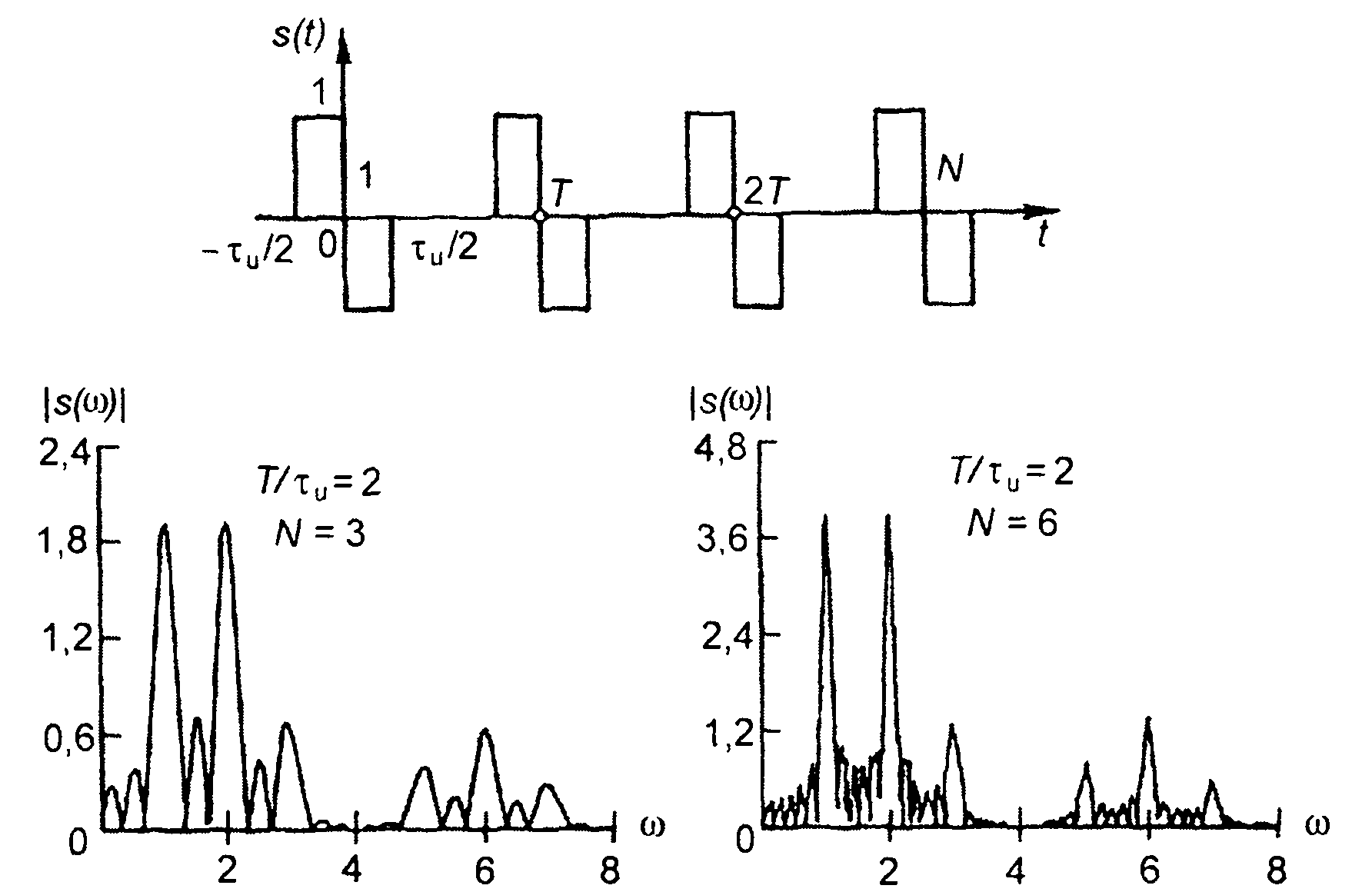
Рис. 3.21

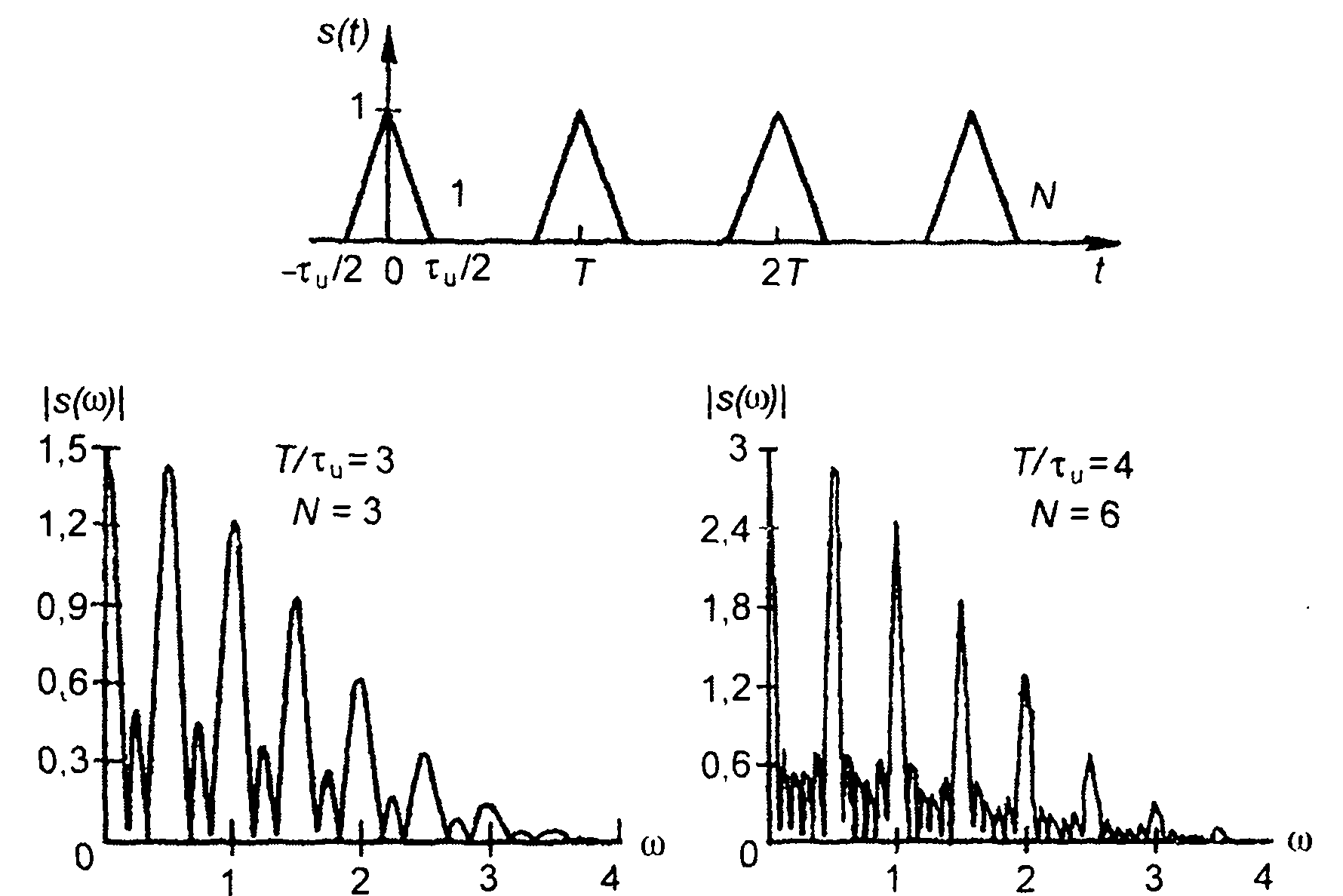
Рис.З. 20

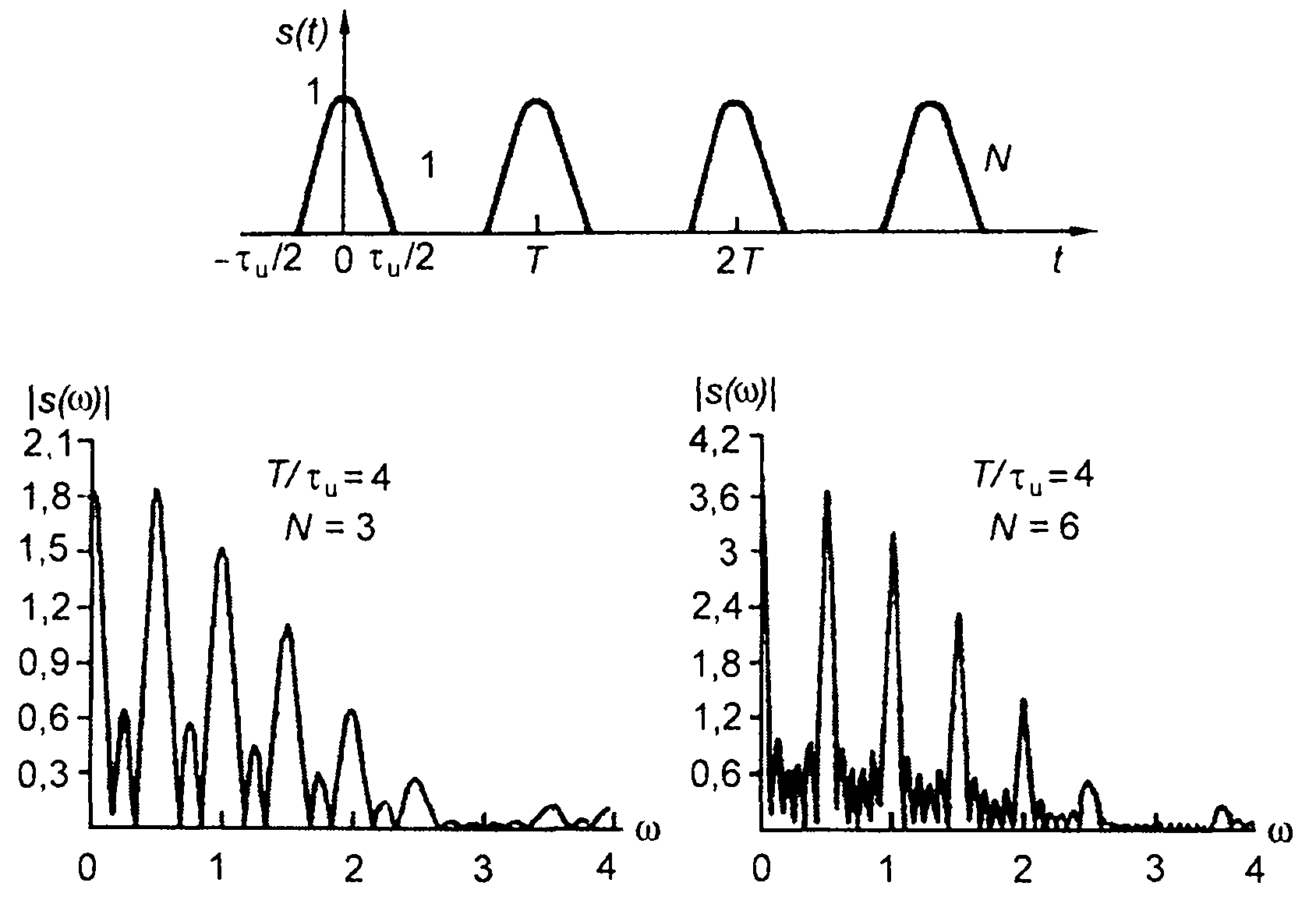
Рис. 3.22 3.6.1.

Преобразование Хартли

Интегральные преобразования Хартли (прямое и обратное) имеют вид

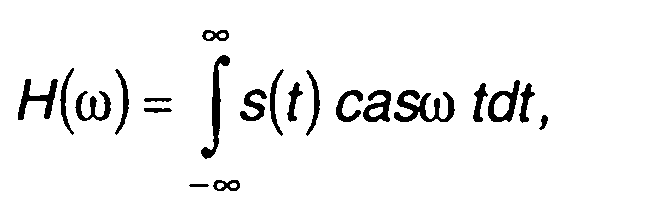(3.80)

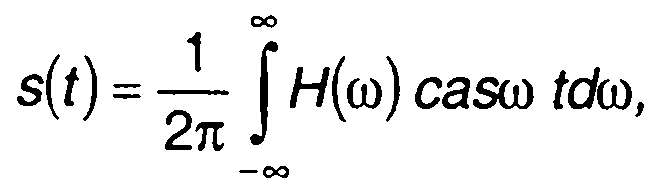(3.81)

где casx = cos x+sin x.

Прямое (3.80) и обратное (3.81) преобразования Хартли явля­ются действительными и обладают взаимной симметрией.

Представляя сигнал как сумму четной и нечетной составляющих, преобразование Хартли запишем в виде

(3.82)

Если сигнал описывается четной функцией s_ч (t), то из (3.80)

получим

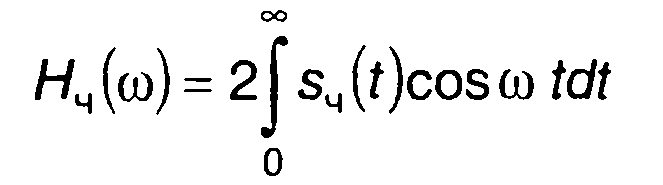(3.83)

Для нечетной функции s_H(t) имеем

(3.84)

Сравнение выражений для преобразований Фурье и Хартли по­зволяют установить взаимосвязь между ними - между Н(ω) и S(ω) :

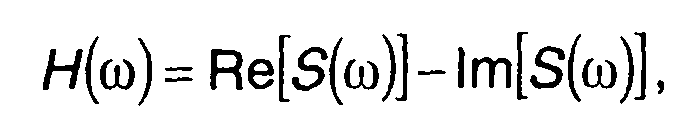(3.85)

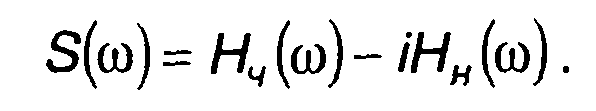
Из (3.85) следует, что для сигнала, описываемого четной функ­цией,

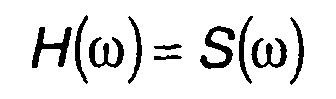(3.86)

а для сигнала, описываемого нечетной функцией,

(3.87)

Свойства преобразования Хартли отражены в табл. 3.4. Там же для сравнения приведены соотношения, характеризующие свойст­ва преобразования Фурье.

Таблица 3.4.

Свойства преобразования Хартли

3.6.2. Примеры преобразований Хартли некоторых сигналов

Особенности преобразования Хартли иллюстрируют следующие примеры.

1. Прямоугольный импульс.

Для симметричного прямоугольного импульса из (3.83) находим (рис. 3.23)

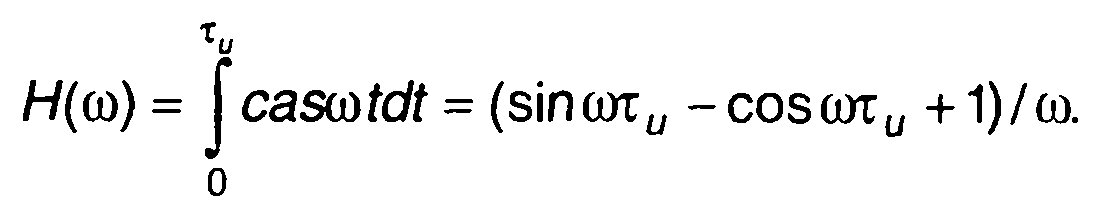
При смещении импульса на интервал т/2 его преобразование Хартли определяется как

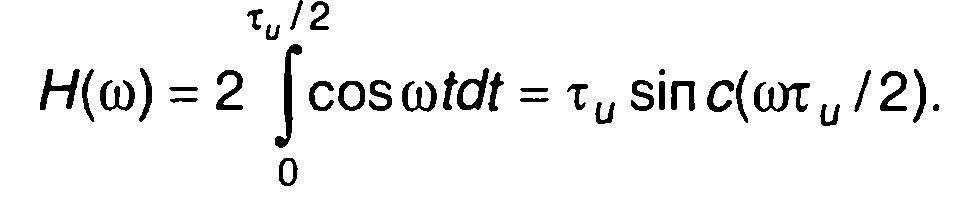
2. Меандровый импульс.

Для меандрового импульса из (3.84) получим (рис. 3.24)

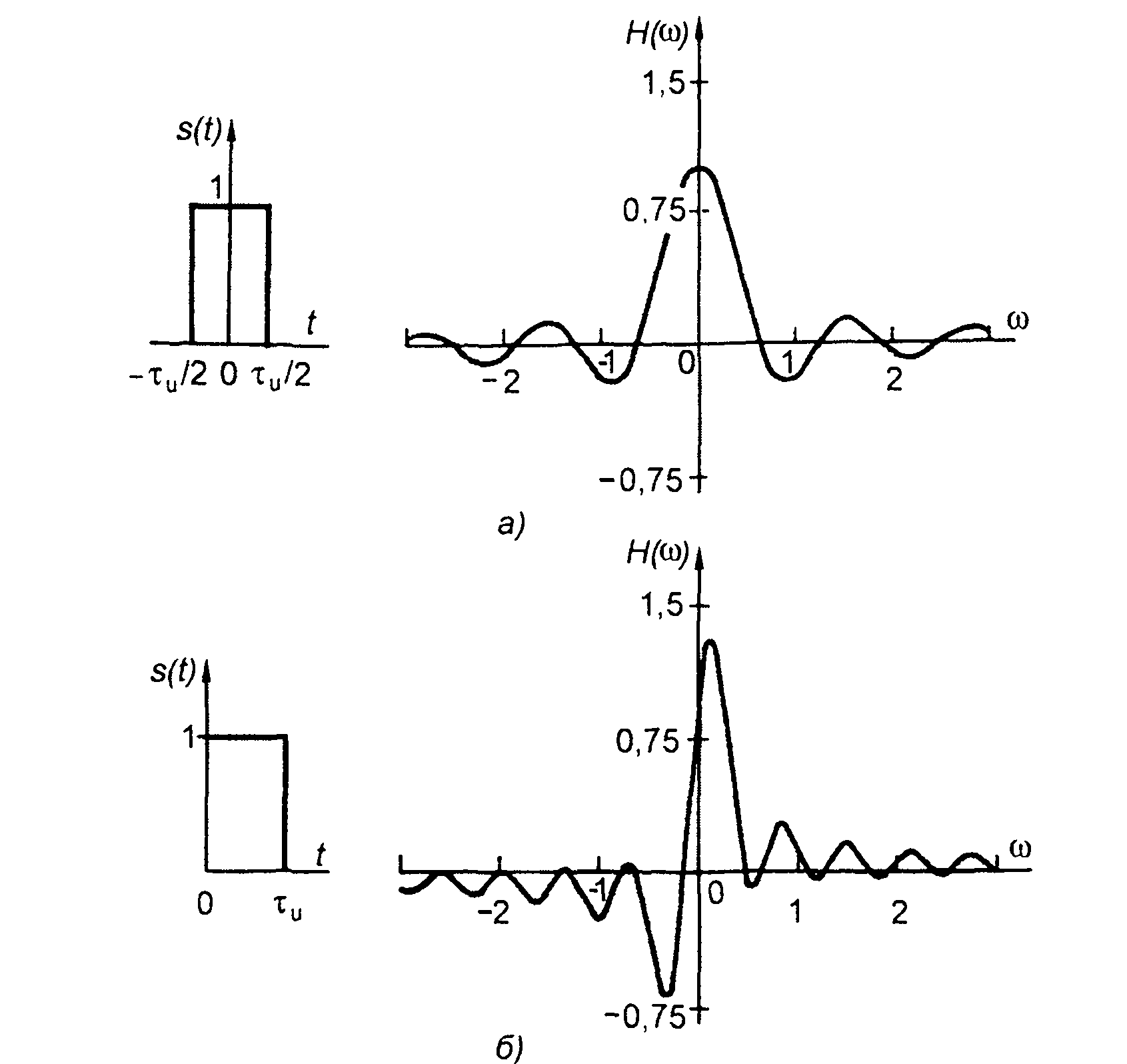
Рис. 3.24

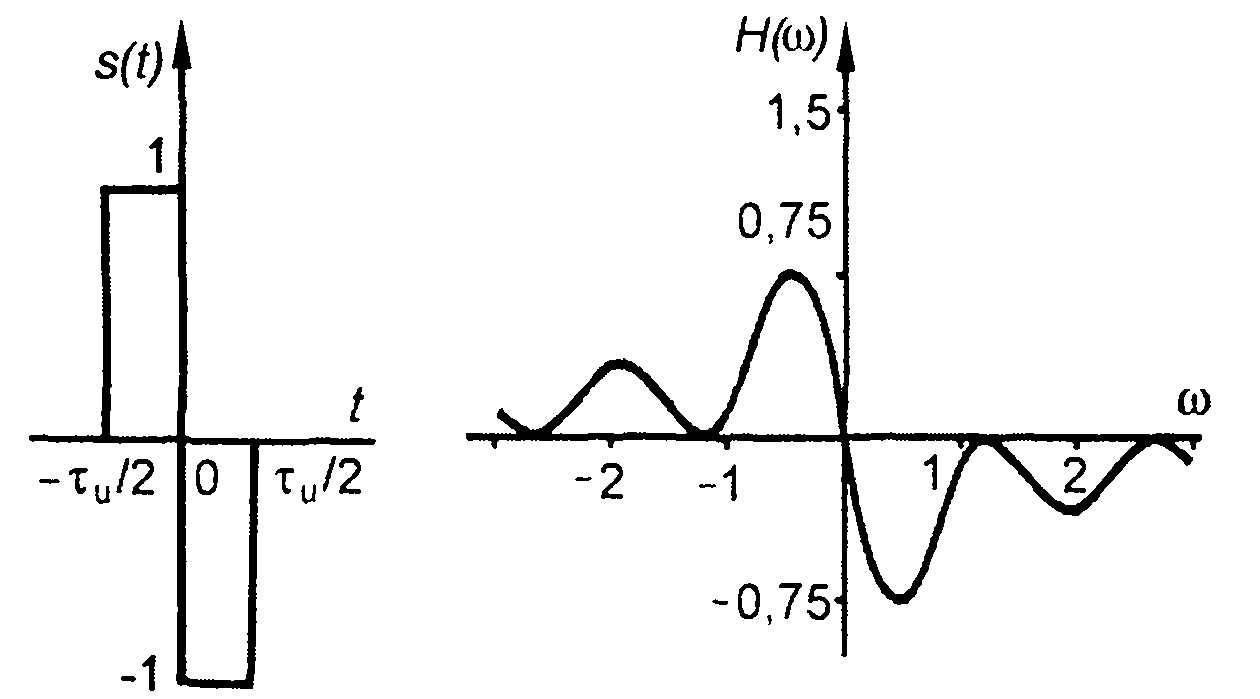
Рис. 3.23

Рассмотрение преобразования Хартли, его особенностей, по­зволяет сделать выводы о практике его применения при анализе сигналов. Действительные величины, получающиеся при использо­вании преобразования Хартли, дают определенные удобства при анализе сигналов и расчете их характеристик на инженерном уров­не. К удобствам преобразования Хартли следует отнести и его симметричность.

Однако преобразование Фурье является более физичным - в большей степени отвечает установившимся представлениям

о спектре как о совокупности гармонических колебаний. Преобразо­вание Хартли дает разложение по сумме двух составляющих, одна из которых сдвинута по фазе относительно другой на π/2.

Преобразование Хартли приводит к более сложным выражени­ям прежде всего для произведения и свертки функций. Указанные операции встречаются довольно часто при анализе сигналов, и это обстоятельство нельзя не учитывать.

Раздел 4.

АНАЛИЗ СИГНАЛОВ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА

При анализе прохождения сигналов через цепи широкое приме­нение нашло преобразование Лапласа. Это объясняется, в част­ности, тем, что класс функций, для которых существует преобра­зование Лапласа, шире, чем тот, для которого существует преобра­зование Фурье, а односторонность преобразования Лапласа при анализе линейных цепей практически не накладывает дополни­тельных ограничений.

Особенности преобразования Лапласа и его применение при анализе сигналов описываются в настоящем разделе.

4.1. Преобразование Лапласа и его свойства

Преобразование Лапласа функции s(t) имеет вид

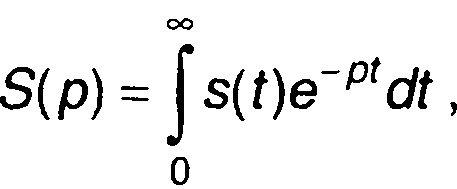(4.1)

где ρ = σ + iω - комплексная или действительная величина.

Интеграл Лапласа отображает функцию s(t) в функцию ком­плексной переменной р. Функция s(t) называется оригиналом, S(ρ) - изображением. Обратное преобразование позволяет вернуться во временную область, перейти от изображения к оригиналу, описывае­мому временной функцией. Соответствие функций по Лапласу обо­значим тем же знаком, который использовался ранее при рассмот­рении преобразования Фурье

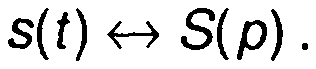
Операциям, проводимым над сигналами во временной области, со­ответствуют операции в области комплексной переменной р. В ряде случаев они оказываются проще, и перевод анализа в область комплексной переменной р позволяет упростить анализ.

Функция s(t), описывающая сигнал, является кусочнонепрерывной, равна нулю при отрицательных значениях t. Условие существования преобразования Лапласа устанавливается нера­венством

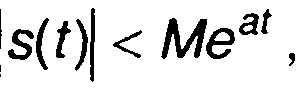(4.2)

где М и а- постоянные.

Неравенство (4.2) ограничивает скорость нарастания функции s(t). При выполнении (4.2) интеграл (4.1) абсолютно сходится для всех ρ, у которых Re[ρ]>a.

Сравнивая преобразования Лапласа и Фурье, отметим, что если преобразование Лапласа существует для функций, удовлетворяю­щих условию (4.2), то для существования преобразования Фурье требуется сходимость интеграла

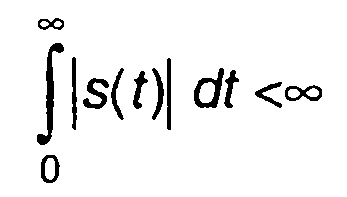(4.3)

Условие сходимости интеграла является более жестким. Таким образом, если для функции s(t) существует преобразование Лапла­са, то для нее не обязательно должно существовать преобразова­ние Фурье. Условию (4.2) удовлетворяют, в частности, функции cosωt и sinωt (t > 0). Для них а можно положить равным нулю: │s(t)│<M. Указанному условию удовлетворяет и степенная функция tⁿ (n > 0), так как такая функция растет медленнее е^t (lim tⁿ/e^t = 0 при t→∞).

При равенстве действительной части ρ нулю (ρ = iω) интеграл Лапласа переходит в интеграл Фурье для сигнала, обращающегося в нуль при t < 0. Односторонность преобразования Лапласа часто не ограничивает класс рассматриваемых сигналов, прежде всего при анализе их прохождения через цепи.

При анализе сигналов с использованием преобразования Лап­ласа полезно учитывать его свойства. Они аналогичны свойствам преобразования Фурье.

1. Аддитивность.

Если

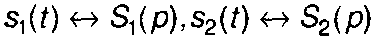
то

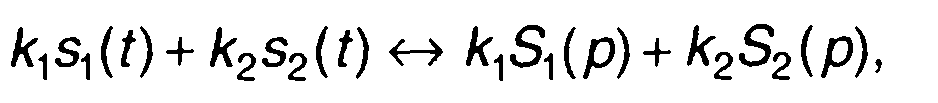(4.4)

где к₁ к₂ - постоянные коэффициенты,

т. е. линейной комбинации оригиналов соответствует такая же комбинация изображений.

2 .Запаздывание.

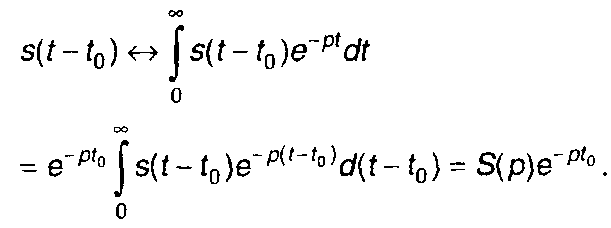(4.5)

3. Подобие.

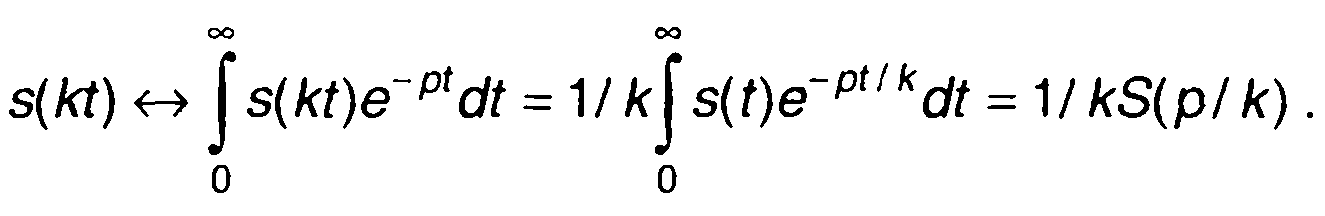(4.6)

4. Смещение.

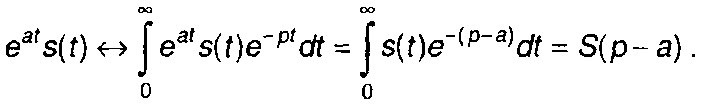(4.7)

5. Дифференцирование оригинала.

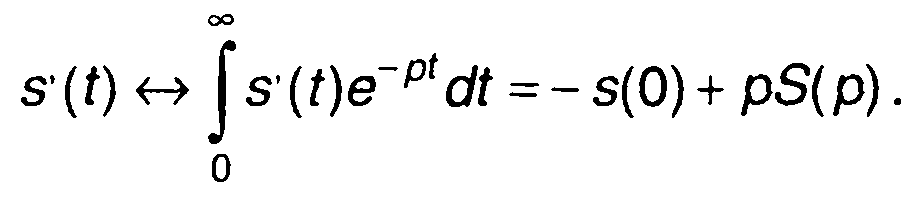
Аналогично можно получить

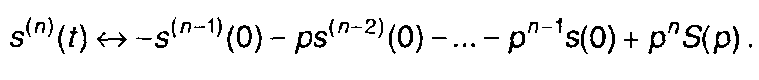(4.8)

При

(4.9)

6. Интегрирование оригинала.

По аналогии с. п. 5 при s(0) = 0 получим

Анализ сигналов на основе преобразования Лапласа

(4.10)

7. Свертка функций.

Свертке функций h(t) и s(t) соответствует произведение изобра­жений

(4.12)

Произведению оригиналов соответствует свертка изображений в комплексной плоскости.

Приведенные основные свойства преобразования Лапласа от­ражены в табл. 4.1.

В качестве примеров рассмотрим преобразования Лапласа не­которых видов сигналов. При этом будем предполагать, что функ­ция, описывающая сигнал, при t < 0 равна нулю.

1. Сигнал s(t) = e^at.

Преобразование Лапласа

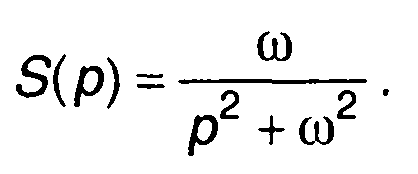
При а = 0 получим изображение ступенчатой функции

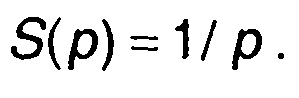
Интеграл Лапласа для ступенчатой функции сходится при Rе[р} > 0.

2. Сигнал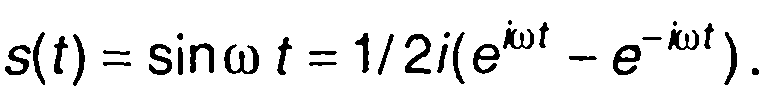

Преобразование Лапласа получим с учетом результата первого примера

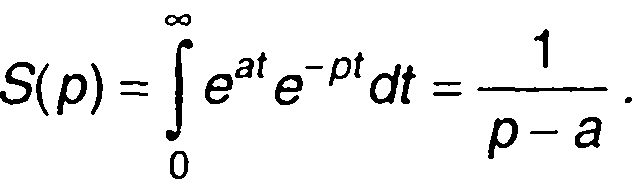
Для сигнала

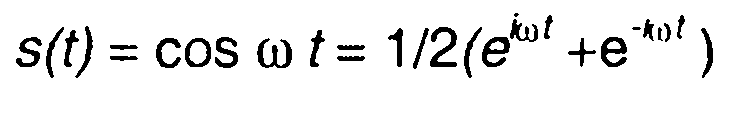
найдем

3. Прямоугольный импульс.

Рассматривая s(t) как разность ступенчатой функции и ступенча­той функции, смещенной на τ, с учетом результата первого приме­ра получим

Таблица 4.1.

Свойства преобразования Лапласа

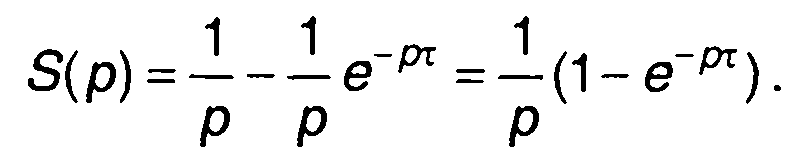
При задержке импульса относительно начала координат на время t₀ с учетом п.2 табл. 4.1 найдем

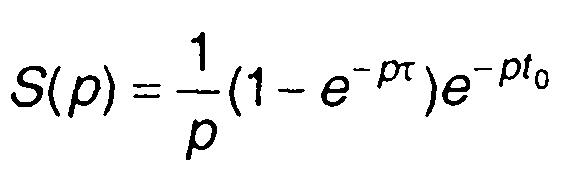
4. Периодическая последовательность прямоугольных им­пульсов.

Используя свойства преобразования Лапласа - аддитивности и запаздывания, получим преобразование Лапласа периодической последовательности идентичных импульсов прямоугольной формы в виде

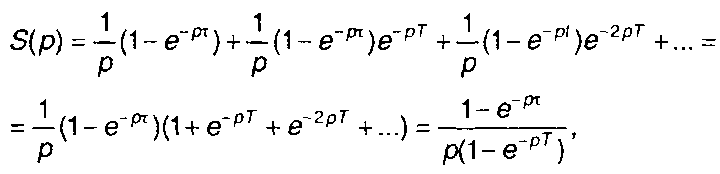
где первое слагаемое представляет изображение первого прямо­угольного импульса, второе - изображение прямоугольного импуль­са, задержанного на время, равное одному периоду T, и т. д.

5. Периодическая последовательность меандровых импульсов. Решение получим аналогично решению предыдущего примера.

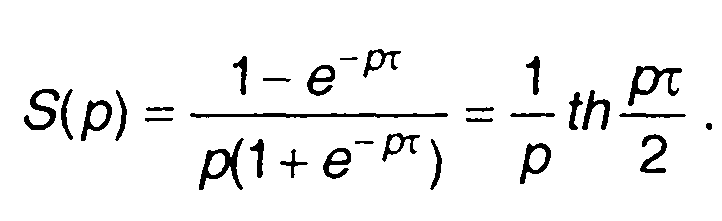
Число примеров преобразований Лапласа увеличивает табл. 4.2.

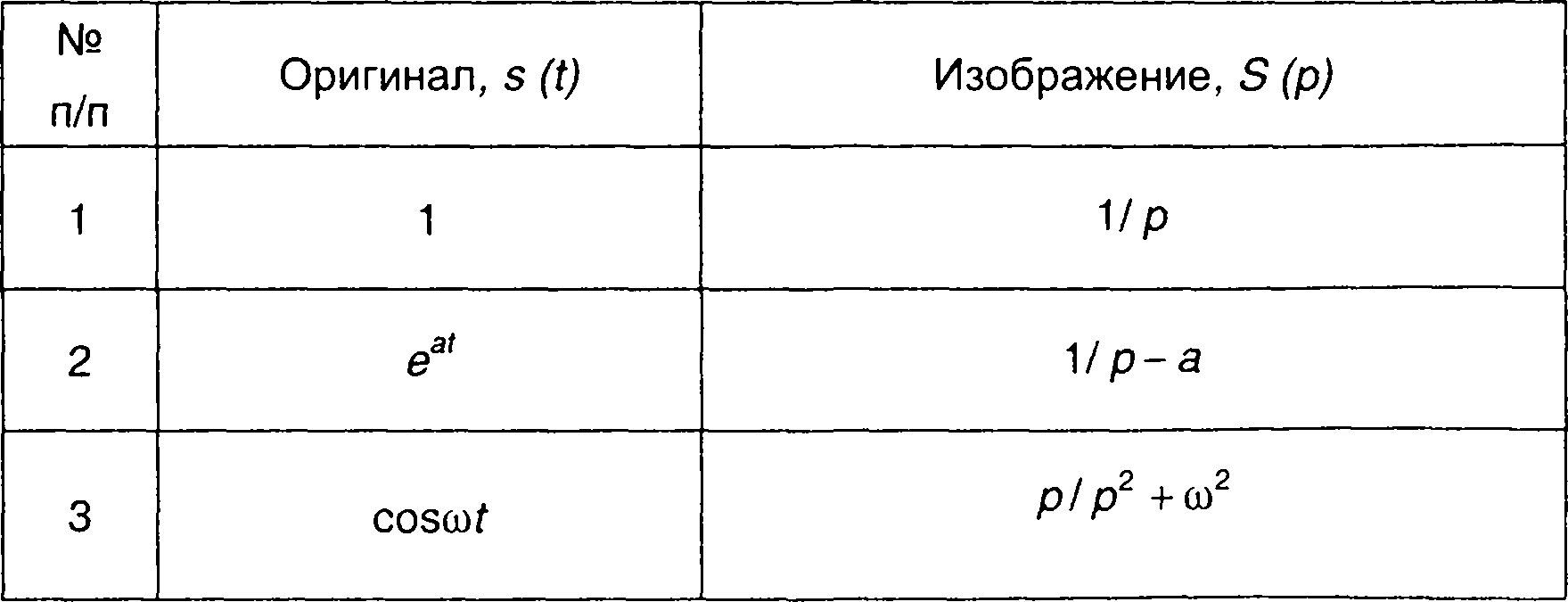
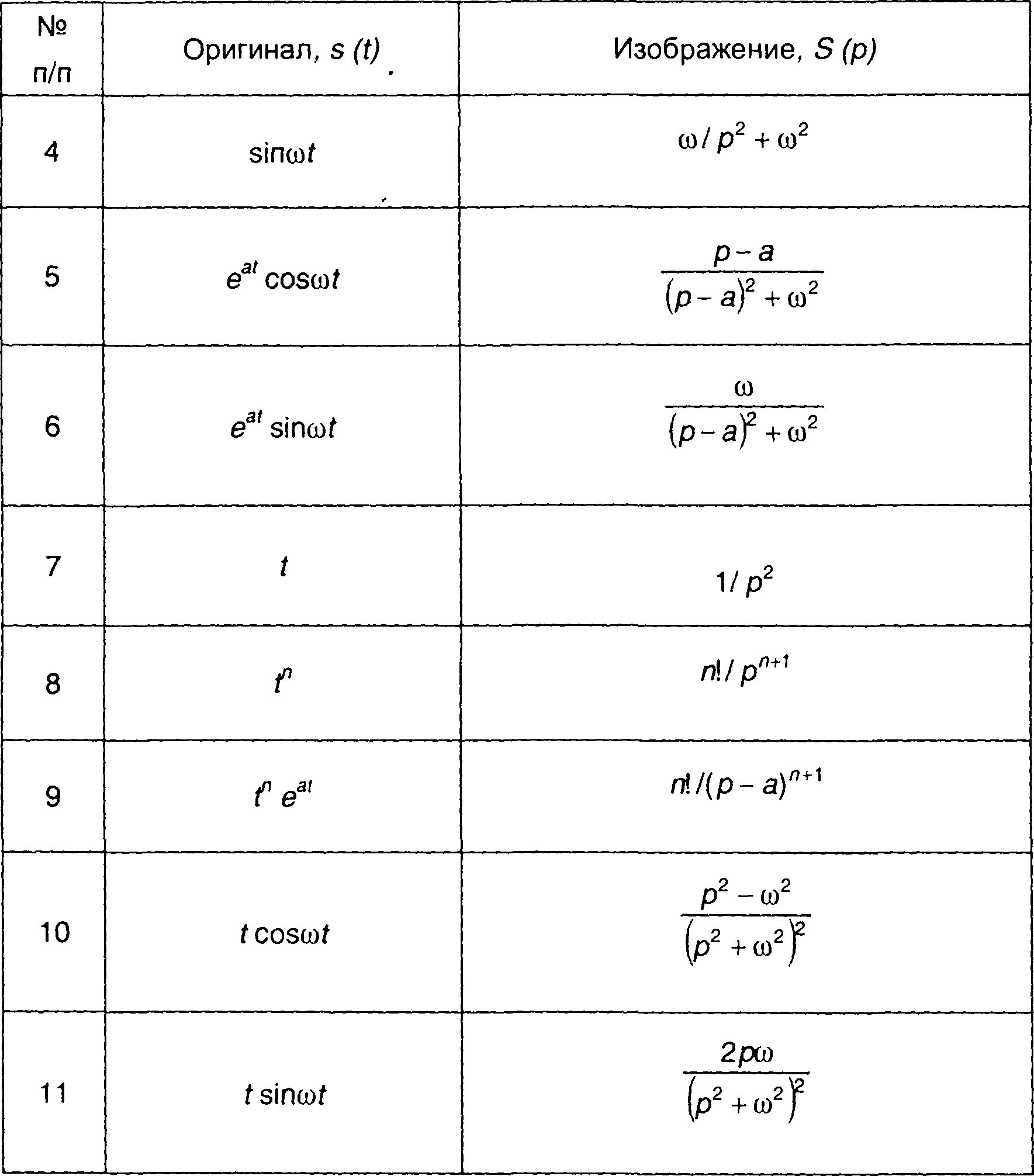
Таблица 4.2.

Сигналы и их преобразования Лапласа

4.2. Обратное преобразование Лапласа

Переход от изображения S(p) к оригиналу - временной функции, описывающей сигнал s(t), производится с помощью обратного пре­образования Лапласа

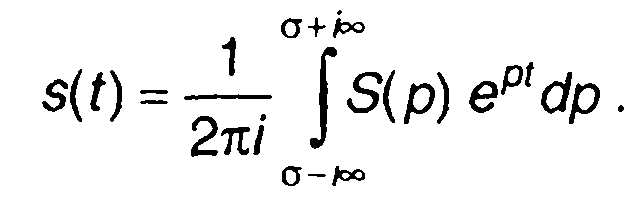(4.13)

Интегрирование в (4.13) происходит по любой бесконечной пря­мой Re[p] = σ, лежащей в области абсолютной сходимости интегра­ла Лапласса от s(t).

Вычисление интеграла (4.13) производится с использованием теоремы о вычетах:

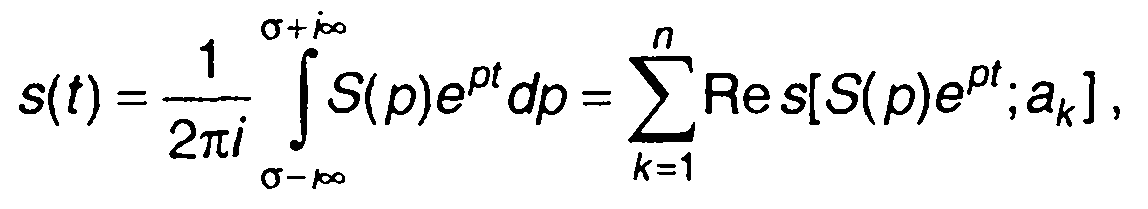(4.14)

где а_к - особые точки функции S(p); Res[f(z),a] - вычет функции f(z) относительно точки а.

Суммирование в (4.14) производится по всем особым точкам. В особой точке а предел функции f(z) либо равен бесконечности, либо функция вообще не имеет предела. В первом случае эту точку называют полюсом функции f(z) , во втором - существенно особой точкой. Если точка z = а является полюсом функции f(z), то она яв­ляется нулем функции 1 /f(z).

Рассмотрим применение (4.14) к достаточно общему случаю описания сигналов в области параметра р простой рациональной дробью

где А(р), В(р) - многочлены, степень многочлена А(р) меньше сте­пени В(р).

Предполагается, что многочлены А(р) и В(р) не имеют общих кор­ней, и дробь не сократима. Функция S(p) имеет конечное число осо­бых точек. Эти точки являются нулями знаменателя В(р), следова­тельно, полюсами функции S(p). Использование выражения для вы­чета в полюсе любого порядка приводит к следующему выражению:

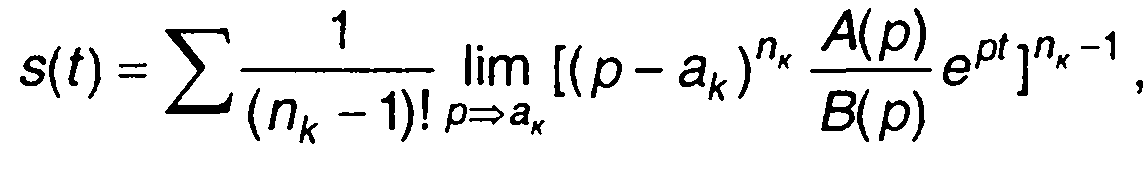(4.15)

где а_k- нули знаменателя В(р)\ n_к- их кратность.

Формула (4.15) называется формулой разложения.

Знаменатель В(р) содержит множитель (р-а_k)ⁿ_k , и его можно представить в виде

(4.16)