ДЕТЕРМИНИРОВАННЫЕ СИГНАЛЫ 1 страница

СИГНАЛЫ И ИХ ПРЕДСТАВЛЕНИЕ

Сигналом будем называть физический процесс, несущий ин­формацию или предназначенный для ее передачи. В зависимости от частоты несущего колебания различают сигналы звукового, ра­дио, оптического и других диапазонов. Объектом изучения радио­техники являются радиосигналы. Их частоты лежат в интервале от

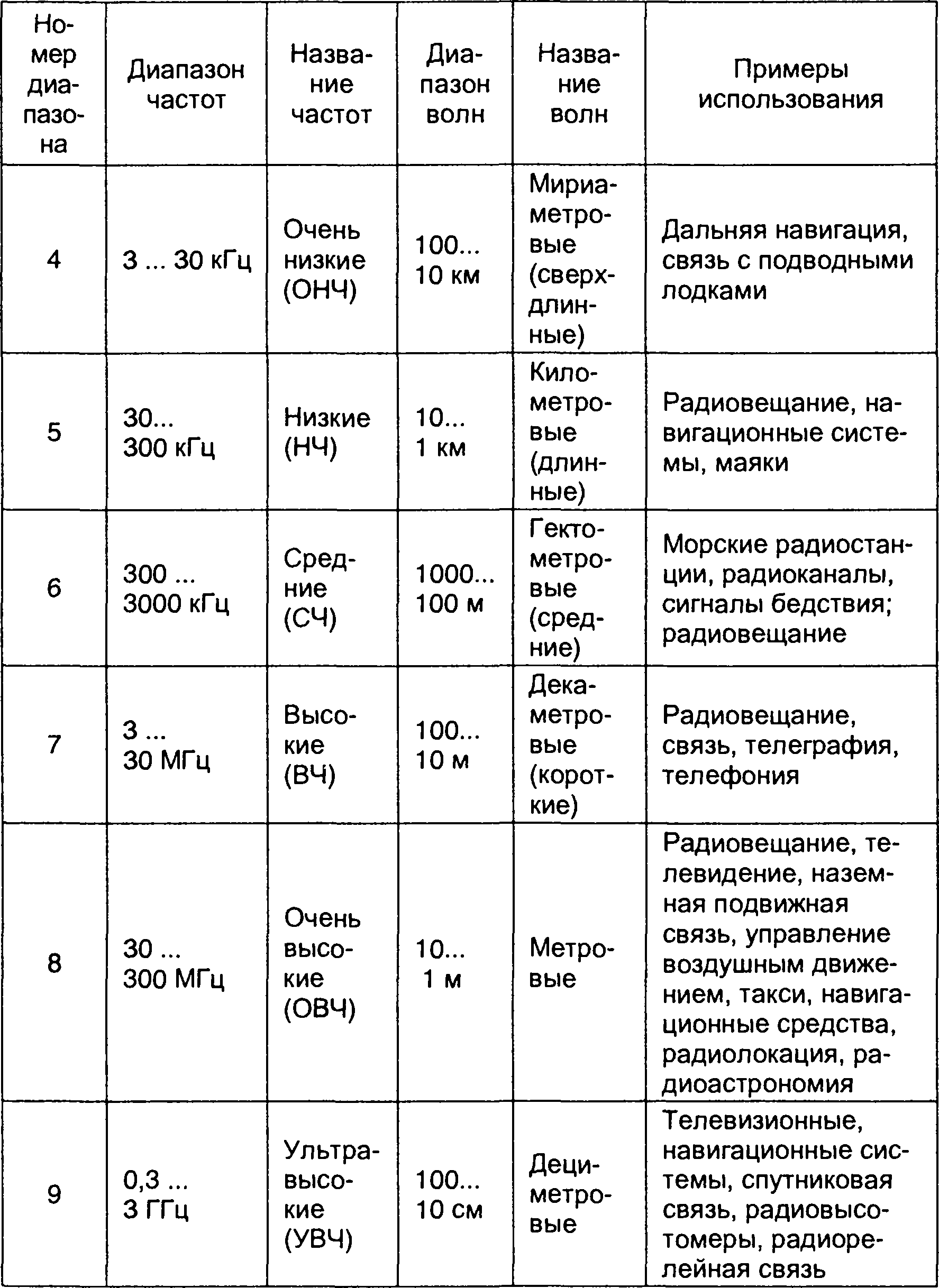
3 кГц до 3000 ГГц. Этот интервал разбит на девять диапазонов, ка­ждый из которых занимает полосу от 0,3-10ⁿ до 3-10Гц (4 ≤ п ≤ 12) (табл. 1.1).

Математический аппарат, используемый при анализе сигналов, позволяет проводить исследования без учета природы сигналов. Однако для понимания содержания характеристик сигналов удоб­нее обращаться к их физическому наполнению. С учетом этого в дальнейшем сигнал будем рассматривать как колебание в радио­технической цепи.

Математическая модель сигнала, как правило, представляет функцию времени, задаваемую в виде аналитического выражения, графика или таблицы. Термин «сигнал» обычно и используется как эквивалентный временной функции, описывающей колебание. Та­кое описание сигнала является наиболее распространенным, но оно не исключает и другие формы представления сигналов.

Полезным является представление сигнала в виде взвешенной суммы более простых составляющих - разложение временной функции, описывающей сигнал, в ряд по системе базисных функ­ций. Такое разложение позволяет свести анализ сложного сигнала к анализу его более простых составляющих. С другой стороны, представление сигнала в виде ряда может использоваться и как исходное при его описании.

Для временной функции, описывающей сигнал и удовлетворяю­щей некоторым условиям, возможно интегральное преобразование. Интегральное преобразование позволяет перейти от временной области определения сигнала к области выбранного параметра.

Сигналы и их представление

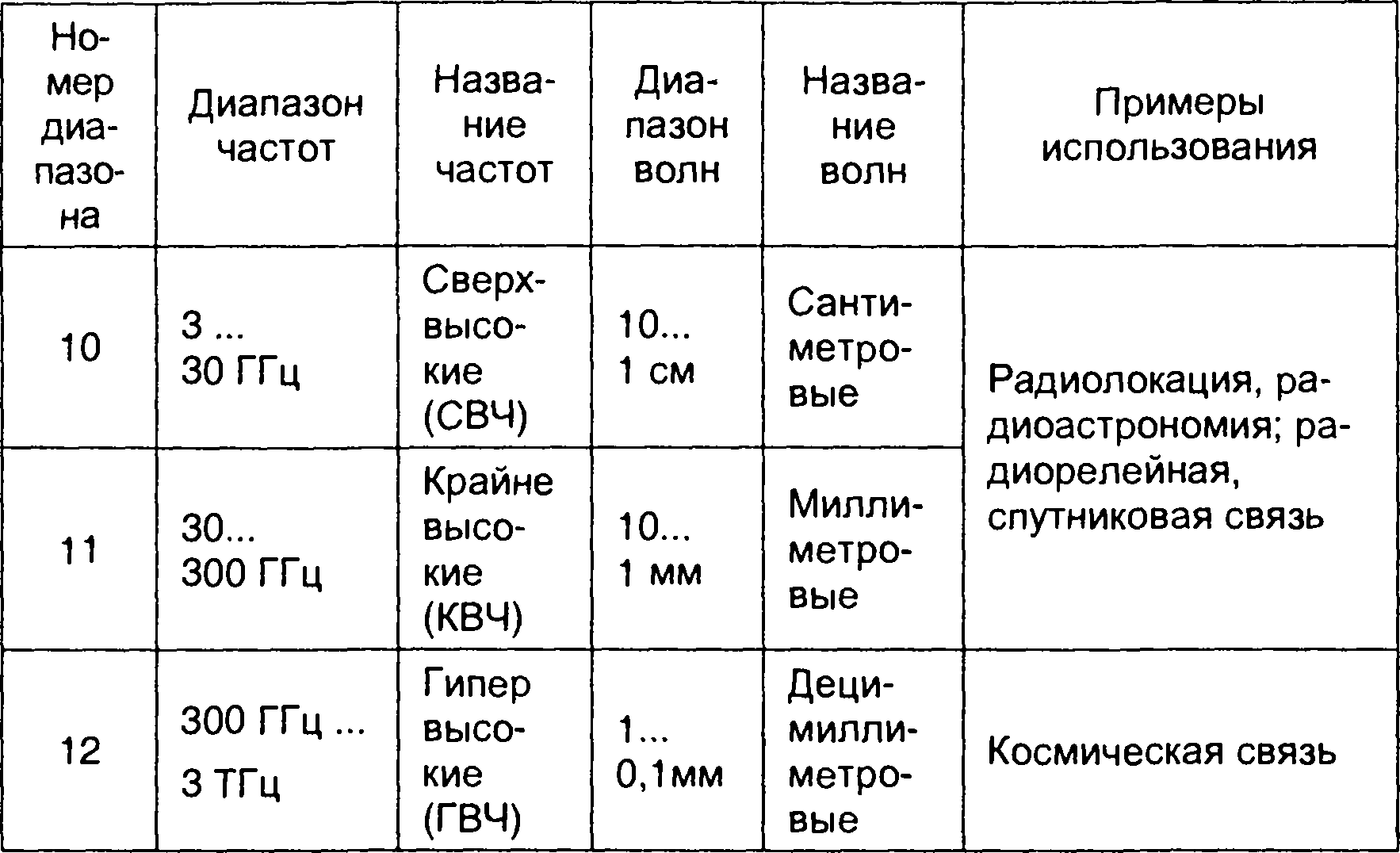
Таблица 1.1.

Классификация диапазонов частот

Раздел 1

В ряде случаев анализ в области выбранного параметра оказы­вается более простым и, следовательно, предпочтительным в ис­следовательской практике. Формула обращения интегрального преобразования позволяет осуществить обратный переход к вре­менной функции. Интегральное преобразование может быть исход­ным при задании сигнала.

Описанию сигналов большую образность придает их геометри­ческая интерпретация. Представление сигналов в виде векторов позволяет проводить их исследования известными методами мно­гомерной геометрии.

Указанные формы представления сигналов рассматриваются ниже, более подробно.

1.1. Описание сигналов временными функциями 1.1.1. Действительные сигналы

Разнообразие возможных видов сигналов отражается прежде всего при их описании во временной области. Примерами аналити­ческого описания сигналов во временной области являются:

гармонический сигнал (рис. 1.1,а)

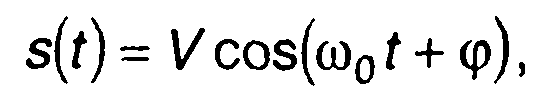
импульсные сигналы:

Сигналы и их представление

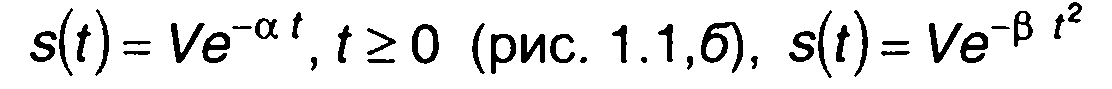(рис. 1.1,в),

модулированные сигналы:

с амплитудной модуляцией

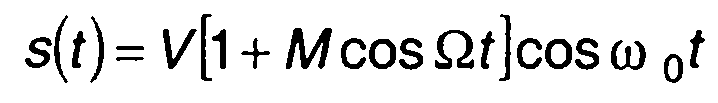, (рис. 1.1,г),

с частотной модуляцией

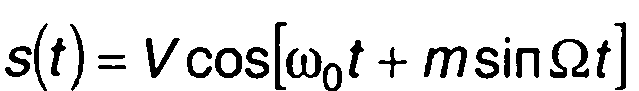, (рис. 1.1,д).

Число примеров описания сигналов временными функциями увеличивают последующие разделы и табл. 3.1.

При описании сигналов полезными оказываются разрывные функции, приведенные в табл. 1.2.

Единичная ступенчатая функция.

Определяется как скачок от 0 до 1 в момент t = О (рис. 1.2,а)

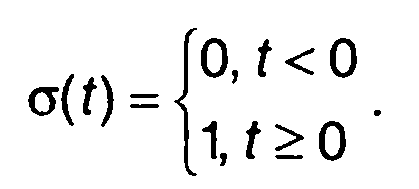(1.1)

Скачок в момент t₀ будет обозначаться как δ(t-t₀) (рис.1.2,б).

Единичную ступенчатую функцию называют также функцией включения, так как умножение δ(t) на временную функцию s(t) (рис. 1.2,в)

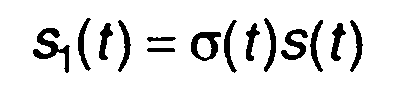(1.2)

означает начало сигнала в момент t = 0. Для сигнала, начинающе­гося в момент t₀, можем записать (рис. 1.2,г):

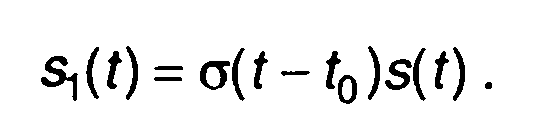(1.3)

Сигнал, ограниченный во времени с двух сторон, может быть представлен в виде (рис. 1.2,д)

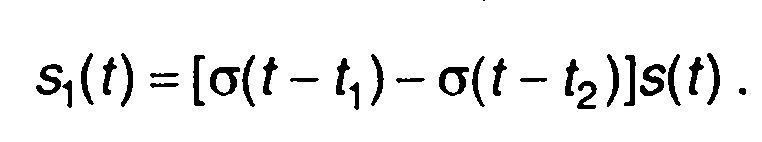(1.4)

Выражение в квадратных скобках в (1.4) описывает прямо­угольный импульс, имеющий амплитуду, равную единице,

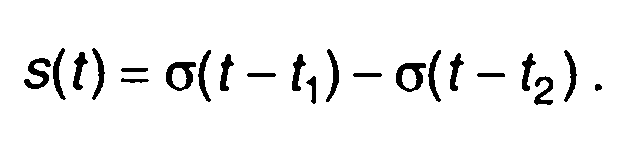(1.5)

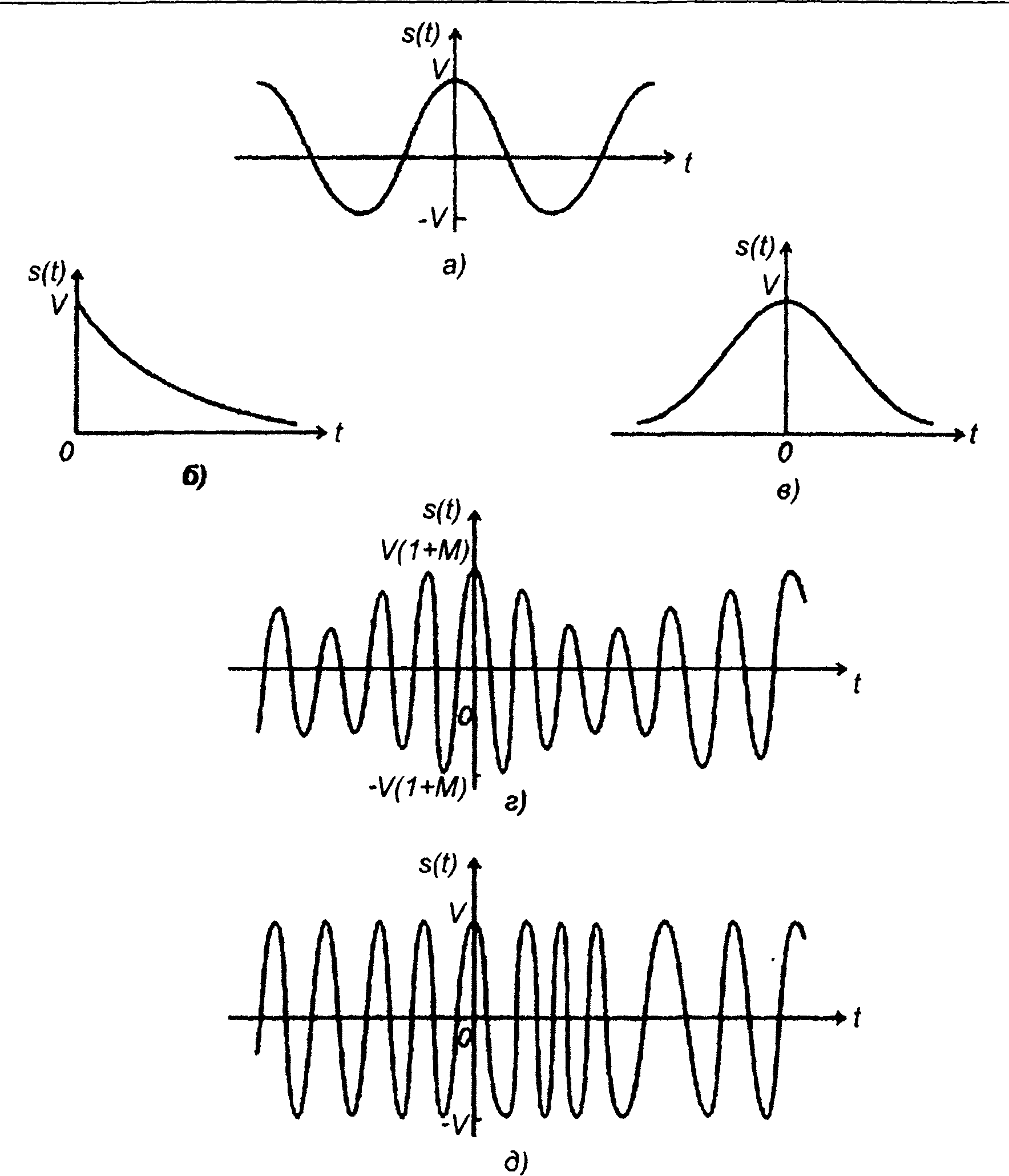
Рис. 1.1

Единичный импульс.

Для функции, описывающей прямоугольный импульс, иногда вводят специальное обозначение

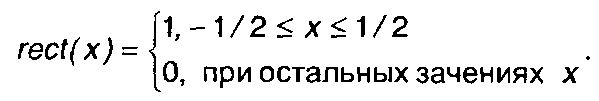(1.6)

Сигналы и их представление

Таблица 1.2.

Разрывные функции

Прямоугольный импульс длительности τ_и определяется как (рис. 1.3 ,а)

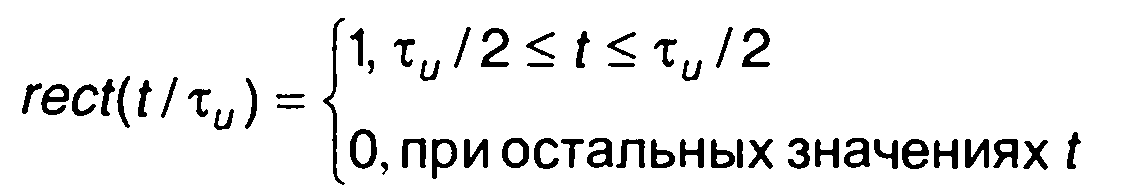(1.7)

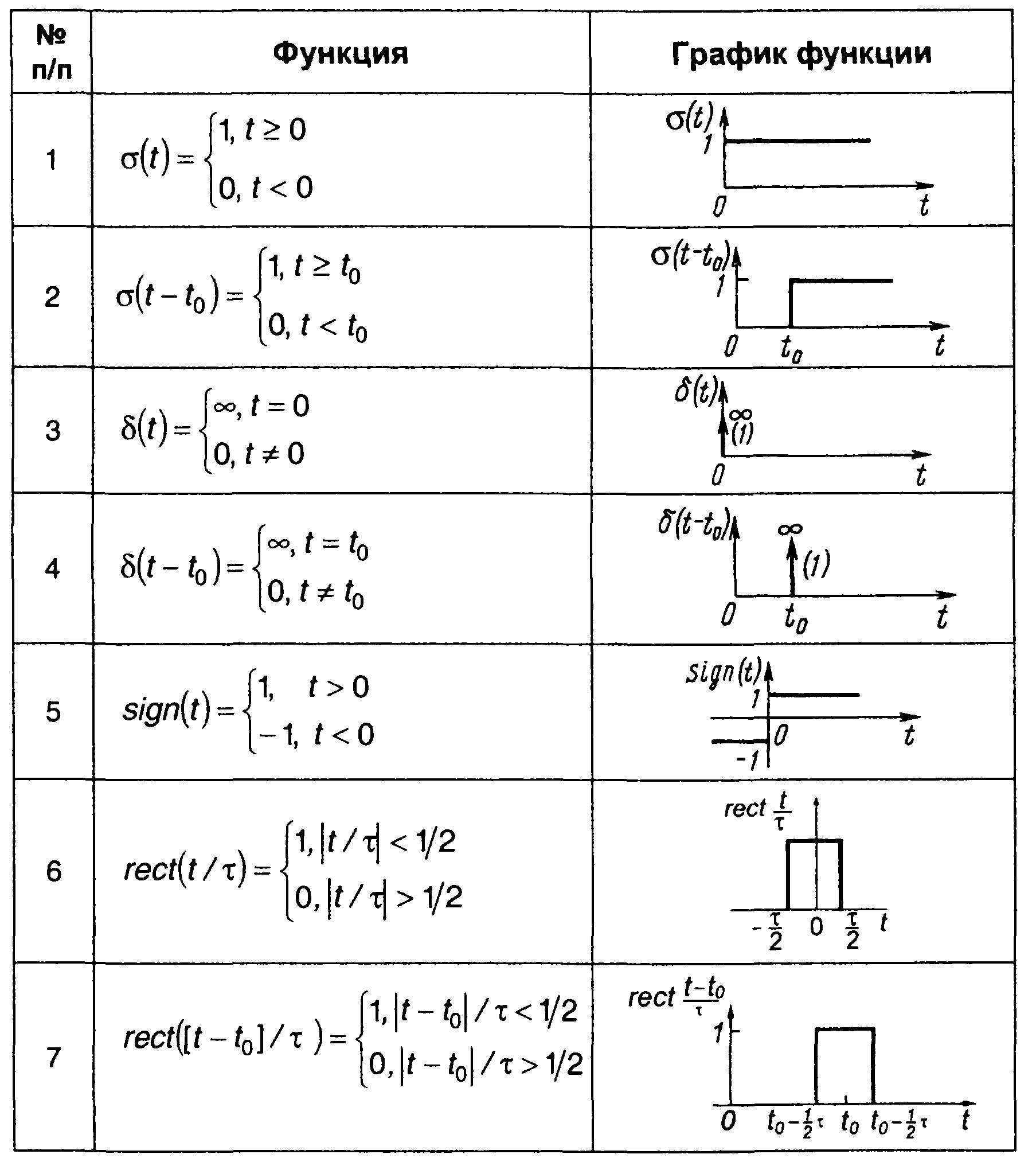
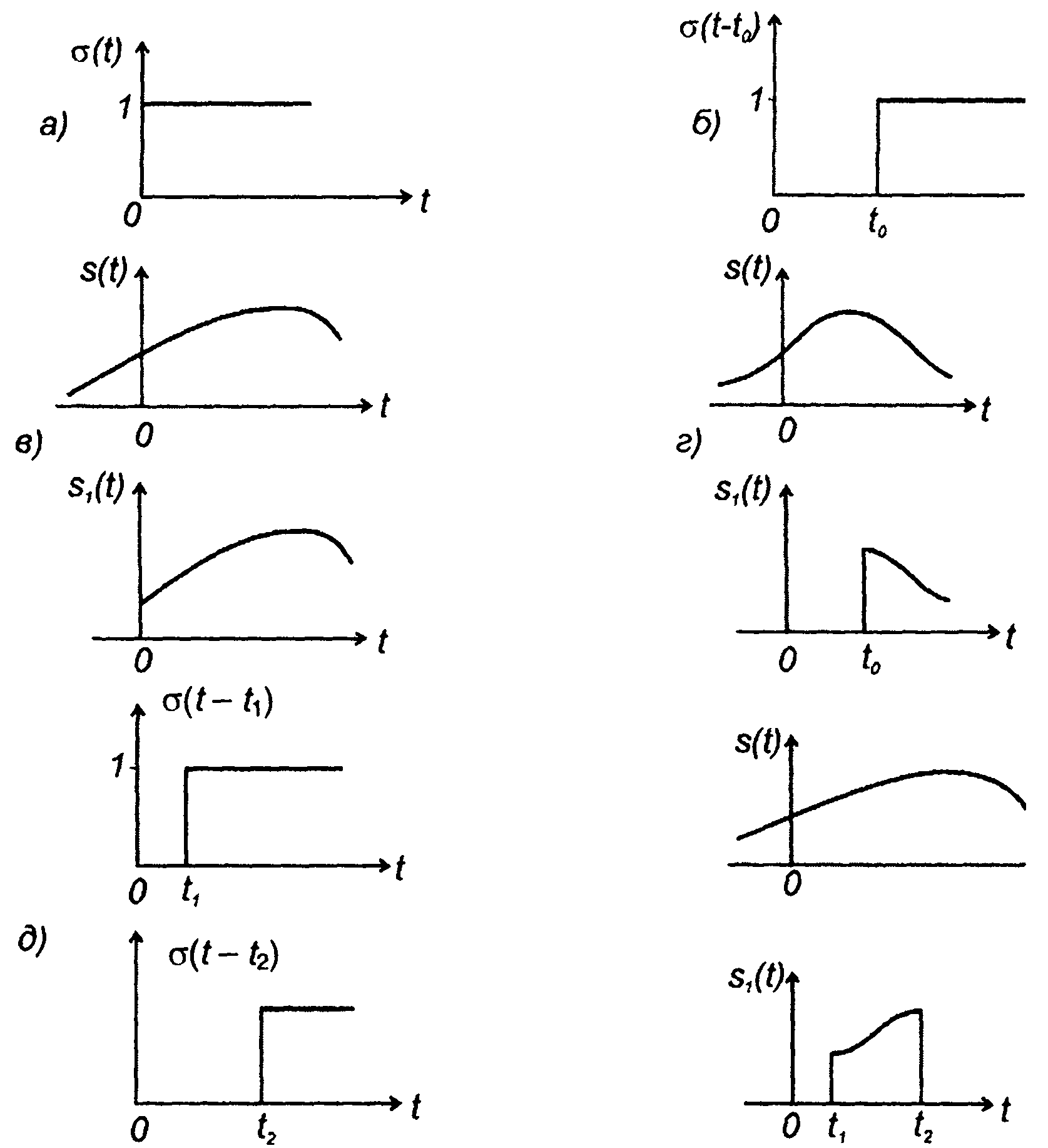
Рис. 1.2

Обозначение запаздывающего на время t₀ импульса имеет вид (рис. 1.3,6)

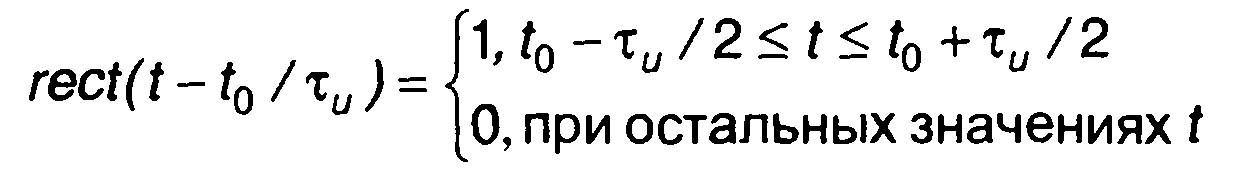(1-8)

Знаковая функция.

Функция знака sign(x) (сигнатура) равна единице, знак которой изменяется при переходе t через нуль (рис. 1.4)

Сигналы и их представление

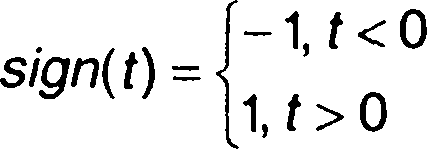(1.9)

Очевидно, функция знака связана со ступенчатой функцией со­отношением

Импульсная функция.

Импульсная или 6-функция представляет импульс бесконечно малой длительности в точке t = О, имеющий бесконечно большую амплитуду и площадь, равную единице:

Импульсную функцию можно рассматривать как предел, к кото­рому стремится прямоугольный импульс длительностью τ и ампли­тудой 1/τ при τ → оо (рис. 1.5).

Импульсная функция представляет производную ступенчатой функции

и наоборот, ступенчатая функция может рассматриваться как инте­грал от импульсной функции

Соотношение (1.14) отражает фильтрующее свойство импульс­ной функции.

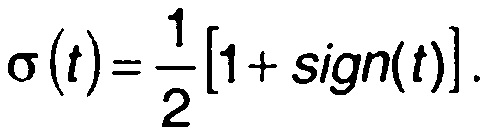(1.10)

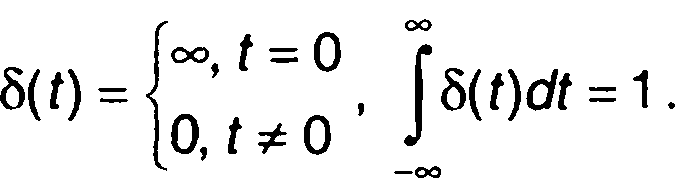(1.11)

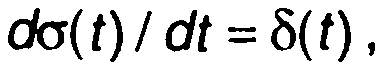(1.12)

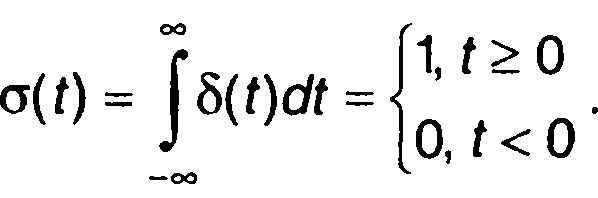(1.13)

Из определения импульсной функции следует

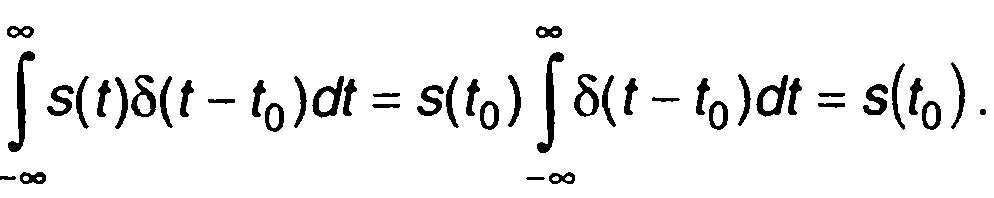(1.14)

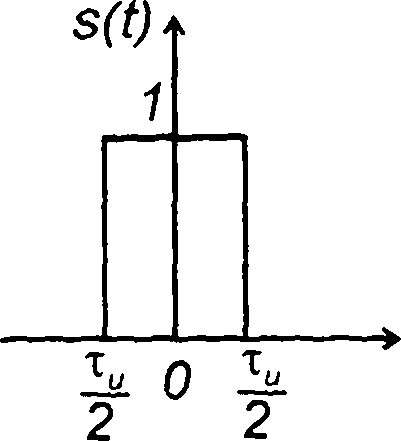
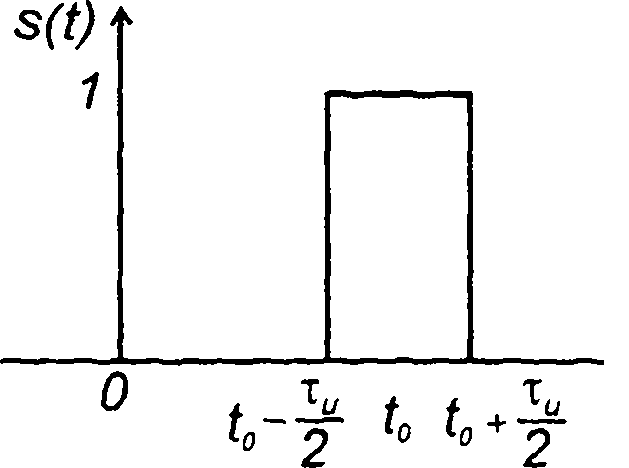
а) б)

Рис. 1.3

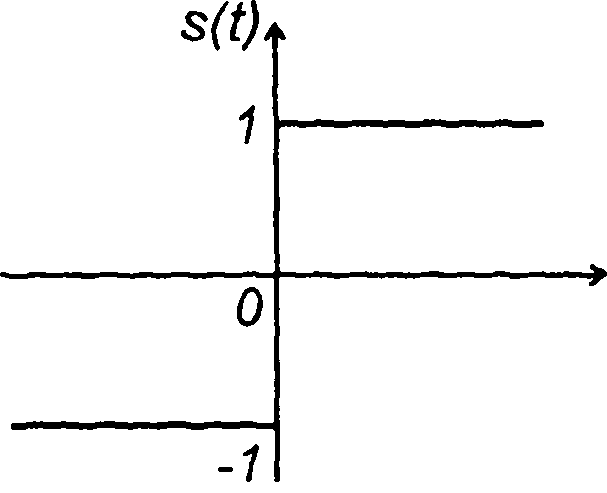
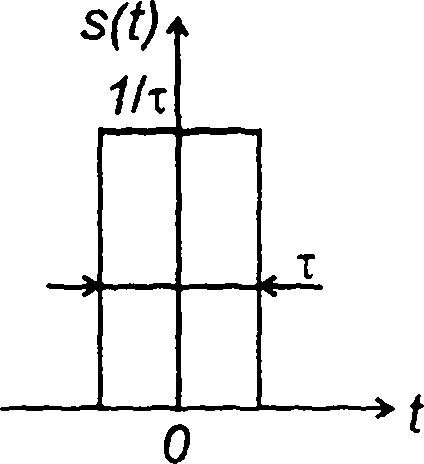
Рис. 1.4 Рис. 1.5

1.1.2. Комплексные сигналы

При описании и анализе некоторых видов сигналов (в первую очередь узкополосных) используется понятие комплексного сигнала

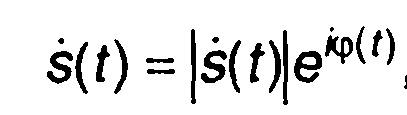(1.15)

где |s(t)|, φ(t) - модуль и аргумент комплексной величины s(t).

Комплексная величина s(t) может быть также представлена в виде

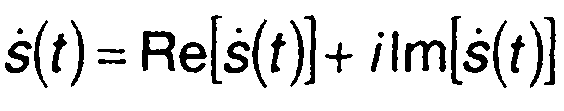(1.16)

где Re, lm - действительная и мнимая части комплексной величины.

Из (1.15) и (1.16) получим:

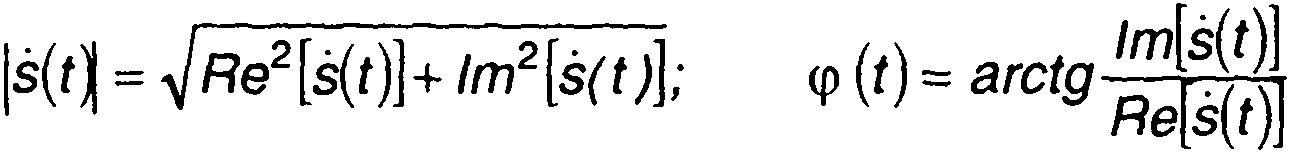(1.17)

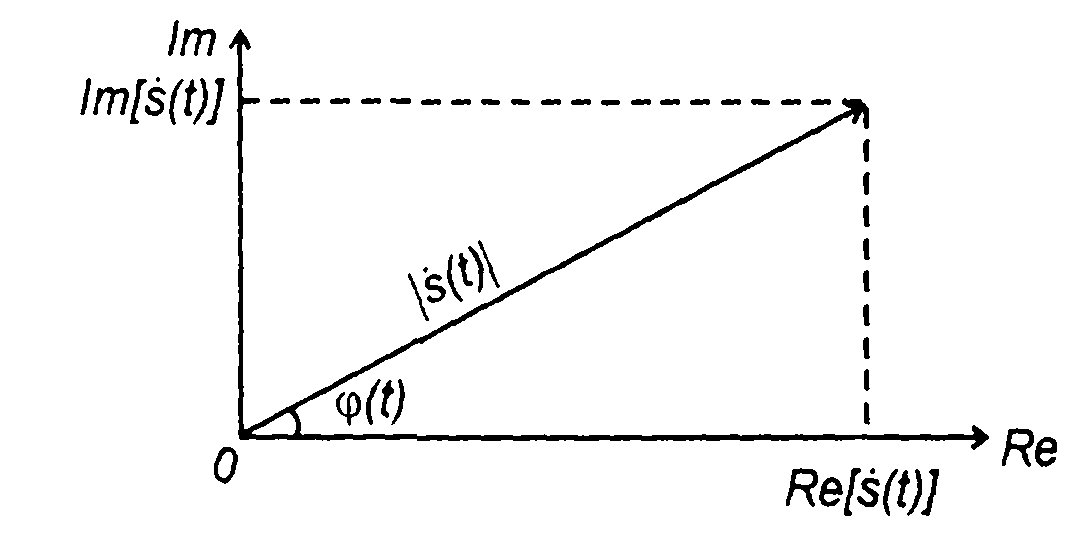
Рис. 1.6

Комплексный сигнал можно рассматривать как вектор на ком­плексной плоскости с действительной осью - осью абсцисс и мни­мой осью - осью ординат (рис.1.6). Такое рассмотрение подключа­ет пространственное воображение, расширяет рамки анализа сиг­налов.

Длина вектора равна модулю комплексной величины, угол между вектором и осью абсцисс равен аргументу φ(t). Проекции вектора на оси координат равны действительной и мнимой частям комплекс­ной величины.

Комплексная форма описания сигнала позволяет в ряде случа­ев упростить математические операции, проводимые с сигналами. Иллюстрацией удобства, связанного с использованием комплекс­ной формы описания сигналов при их анализе, служат последую­щие разделы (начиная с разд. 8).

1.2. Представление сигналов ортогональными рядами

Временная функция, описывающая сигнал s(t), может быть представлена в виде взвешенной суммы, как правило, более про­стых базисных функций φ_n(t)

где с_n - постоянные коэффициенты.

Такое представление сигнала означает, что сигнал рассматри­вается как совокупность элементарных колебаний, взятых с соот­ветствующими коэффициентами. Разложение функции s(t) по сис­теме базисных функций {φ_n(t)} особенно удобно, если система функций является ортогональной. Система функций {φ_n(t)} называ­-

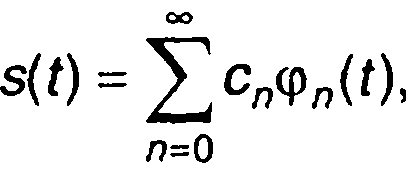(1.18)

ется ортогональной с весом ρ(t) на интервале [t_a, t_b], если выпол­няется следующее равенство:

При ||φ_n|| = 1 система функций {φ_n(t)} называется ортонормированной.

Коэффициенты ряда (1.18) (с учетом (1.19) ) определяются вы­ражением

Разложение s(t) по ортогональной системе функций называется обобщенным рядом Фурье, а коэффициенты ряда - обобщенными коэффициентами Фурье. Совокупность коэффициентов разложения называется спектром сигнала в выбранной системе базисных функций. В обобщенный ряд Фурье может быть разложена любая функция, квадратично интегрируемая на интервале [t_a, t_b].

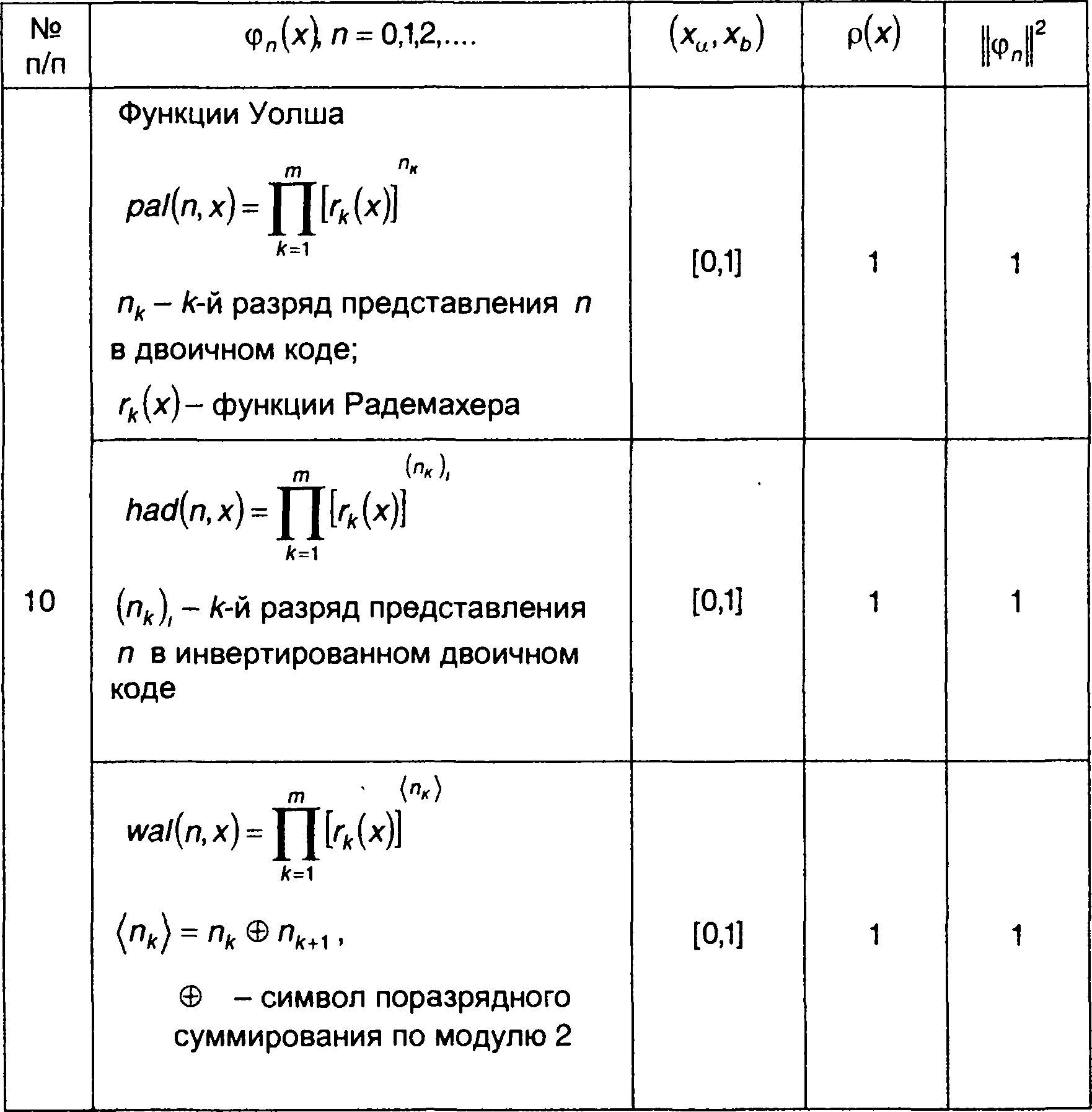
Некоторые виды ортогональных систем базисных функций, ко­торые могут быть использованы при описании и анализе сигналов, приведены в табл. 1.3. Примеры их применения при спектральном анализе сигналов даны в разд. 2.

В практике анализа периодических сигналов наибольшее при­менение получил тригонометрический ряд Фурье, в котором в каче­стве базисных функций выбраны тригонометрические функции

где ω₁ - частота сигнала.

Коэффициенты тригонометрического ряда Фурье (1.21) опреде­ляются выражениями

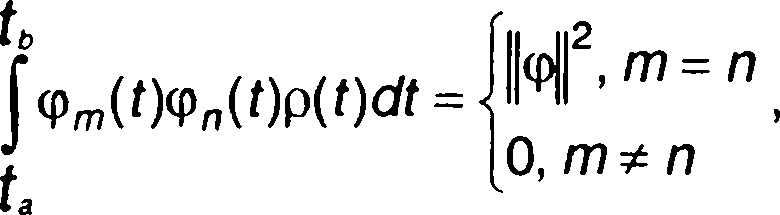(1.19)

где ||φ_n|| - норма функций φ_n(t)-

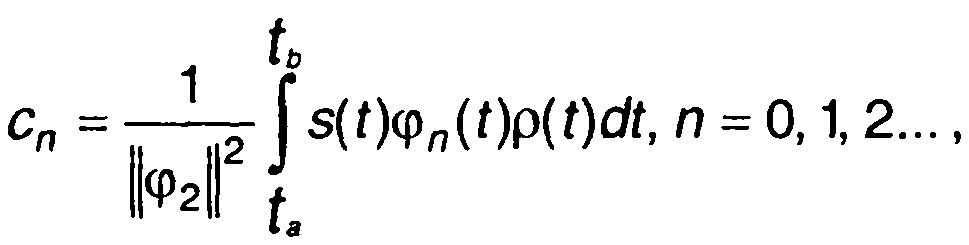(1.20)

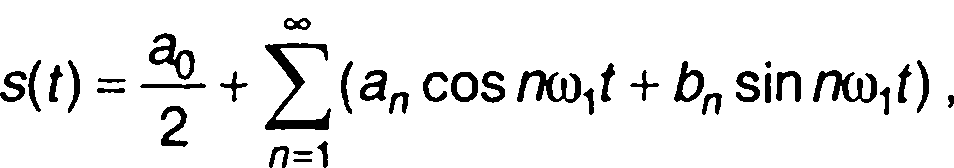(1.21)

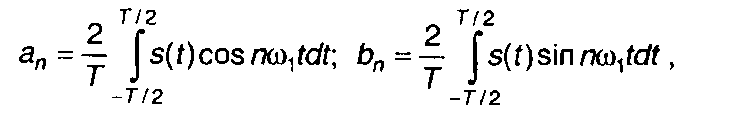
где T = 2π/ω₁ - период сигнала.

Форма записи тригонометрического ряда может быть несколько иной

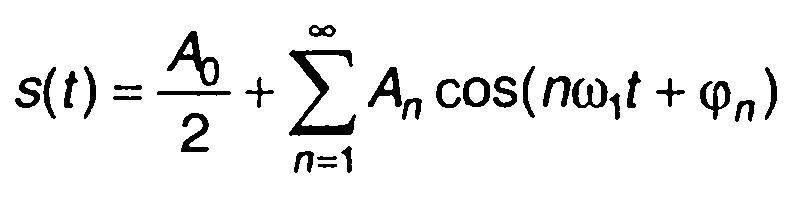(1.23)

где

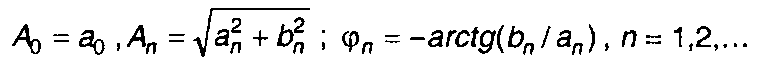(1.24)

При представлении сигнала в виде (1.23) он определяется сово­купностью амплитуд А_n и фаз φ_n. Совокупность амплитуд А_n на­зывается амплитудным спектром, а совокупность фаз φ_n- фазо­вым спектром.

Тригонометрический ряд Фурье описывает разложение сигнала на гармонические составляющие, позволяет проводить анализ сиг­нала в частотной области. Анализ с его использованием называет­ся гармоническим.

В качестве примера рассмотрим сигнал, представляющий пе­риодическое колебание пилообразной формы (рис. 1.7, а). Для него тригонометрический ряд (1.23) имеет вид:

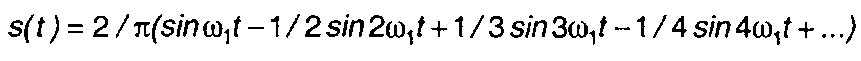
где ω₁ = 2π/Т - частота, Т- период сигнала.

Таблица 1.3.

Ортогональные системы функций

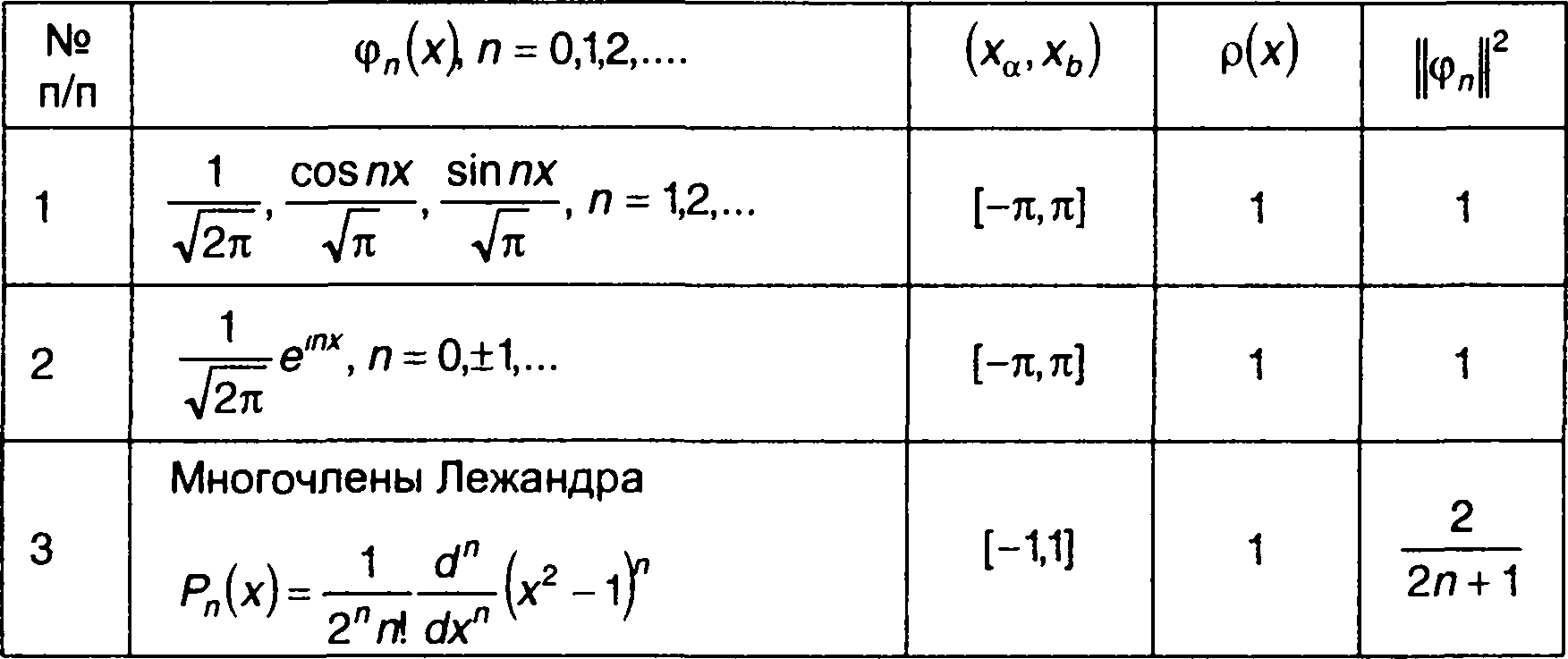
Амплитудный спектр сигнала приведен на рис. 1.7,6. Спектр да­ет представление о распределении амплитуд сигнала по частоте.

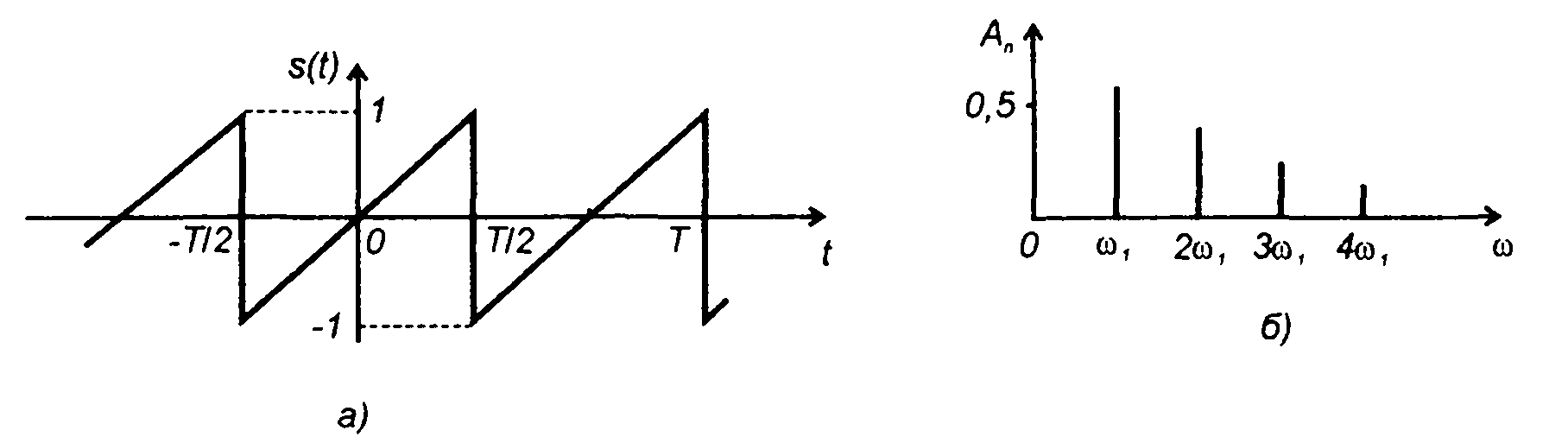
Рис. 1.7

1.3. Интегральное представление сигналов

Одним из представлений сигналов, нашедших применение при их описании и анализе, является интегральное представление сиг­налов.

При некоторых условиях для функции, описывающей сигнал во временной области s(t), существует интегральное преобразование

где ψ(x,t) - заданная функция (ядро интегрального преобразова­ния); Т - область определения функции s(t).

Интегральное преобразование позволяет осуществить переход от временной области определения функции к области параметра х. Операциям над сигналом во временной области соответствуют операции в области параметра х. Операции в области параметра х могут быть проще, следовательно, расширяются возможности про­водимого анализа.

Формула, позволяющая восстановить сигнал s(t) по известной функции S(x), называется формулой обращения интегрального преобразования

где φ(t,x) - базисная функция.

Выражения (1.25) и (1.26) устанавливают взаимно однозначное соответствие между функцией s(t) и ее интегральным преобразова­нием S(x). Функция S(x) является интегральным представлением сигнала, может быть исходной при описании сигнала.

Из известных интегральных преобразований одним из наиболее часто используемых при анализе сигналов является преобразова­ние Фурье

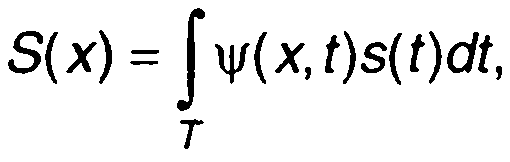(1.25)

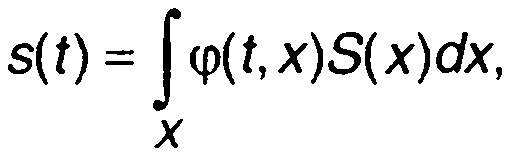(1.26)

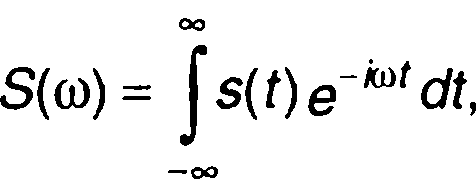(1.27)

где ω - параметр преобразования, частота.

Ему соответствует обратное преобразование

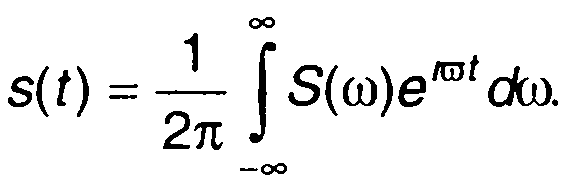(1.28)

Интеграл Фурье (1.28) дает описание сигнала в виде суммы гар­монических составляющих с непрерывной последовательностью частот ω. Спектральный анализ сигналов с использованием такого представления входит в понятие гармонического. Функция S(ω) на­зывается спектральной плотностью или спектром сигнала s(t). С помощью (1.28), имея спектральную плотность, можно перейти к описанию сигнала во временной области.

В общем случае S(ω) является комплексной величиной. Как ком­плексная величина она записывается в виде

где |S(ω)|, φ(ω) - модуль и аргумент комплексной величины,

амплитудный и фазовый спектры сигнала.

Примером служит преобразование Фурье временной функции, описывающей сигнал, экспоненциального вида

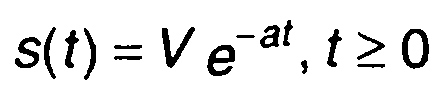
Преобразование Фурье s(t):

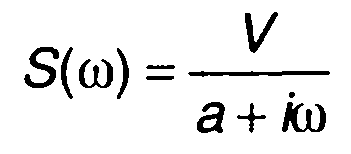
Амплитудный и фазовый спектры сигнала описываются выраже­ниями

(1.29)

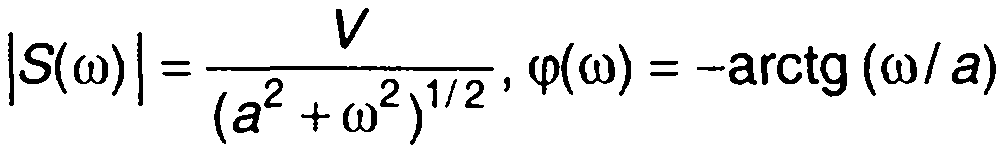
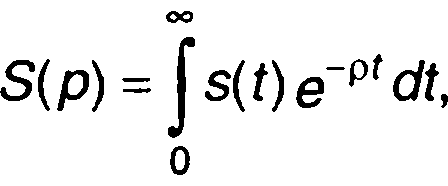(1.30)

где ρ = σ + iω - комплексная величина.

Графики амплитудного и фазового спектров сигнала представ­лены на рис. 1.8. Они дают представление о плотности распреде­ления амплитуд и фаз сигнала по частоте.

Другим интегральным преобразованием, широко используемым при анализе сигналов, является преобразование Лапласа

23

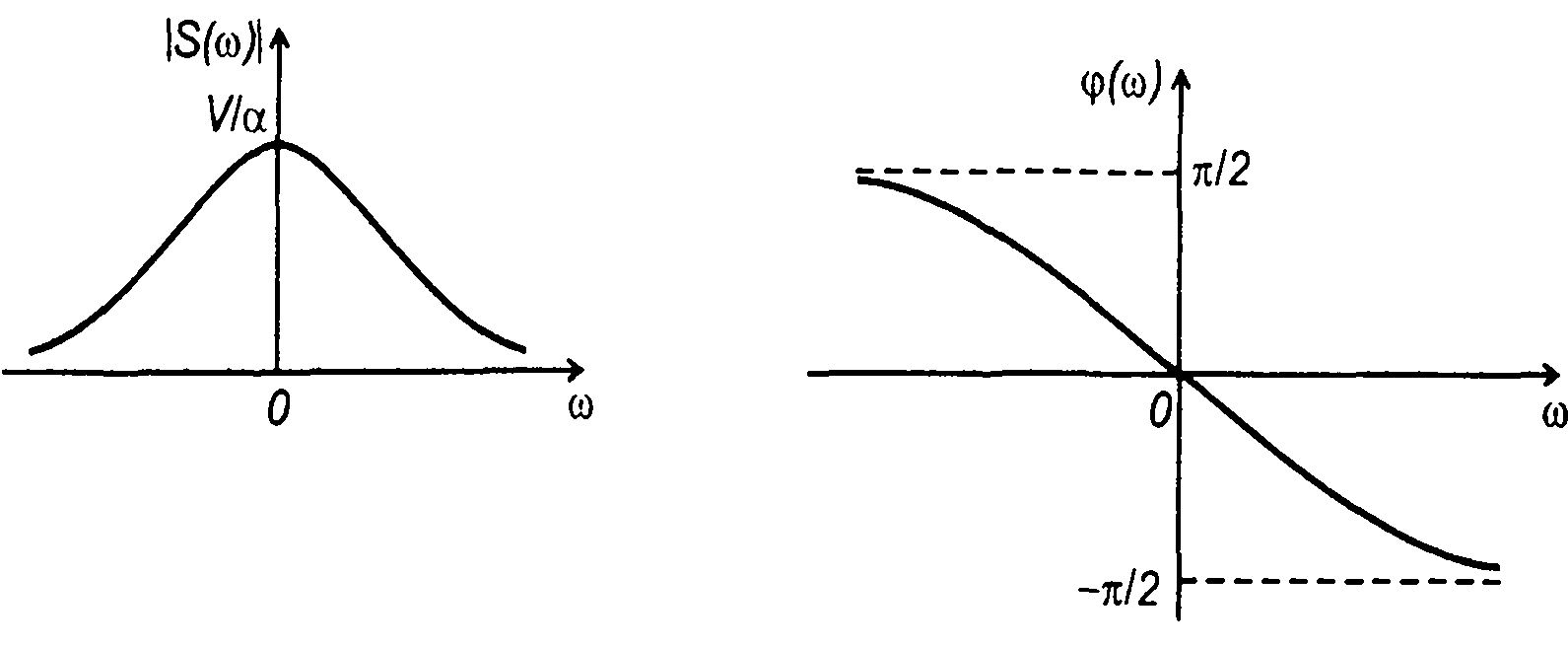
Преобразование Лапласа в ряде случаев расширяет возможно­сти анализа сигналов по сравнению с преобразованием Фурье, ча­ще используется при анализе прохождения сигналов через цепи.

Переход от изображения сигнала S(p) к оригиналу s(t) осуществ­ляется с помощью обратного преобразования Лапласа

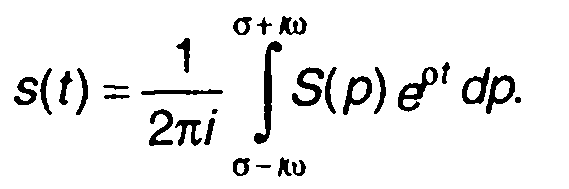(1.31)

При σ = 0 выражение (1.30) переходит в интеграл Фурье для функции s(t), равной нулю при t< 0.

Возможны и на практике используются другие виды интеграль­ных преобразований. Некоторые из них, наиболее распространен­ные, приведены в табл. 1.4.

Таблица 1.4.

Интегральные преобразования

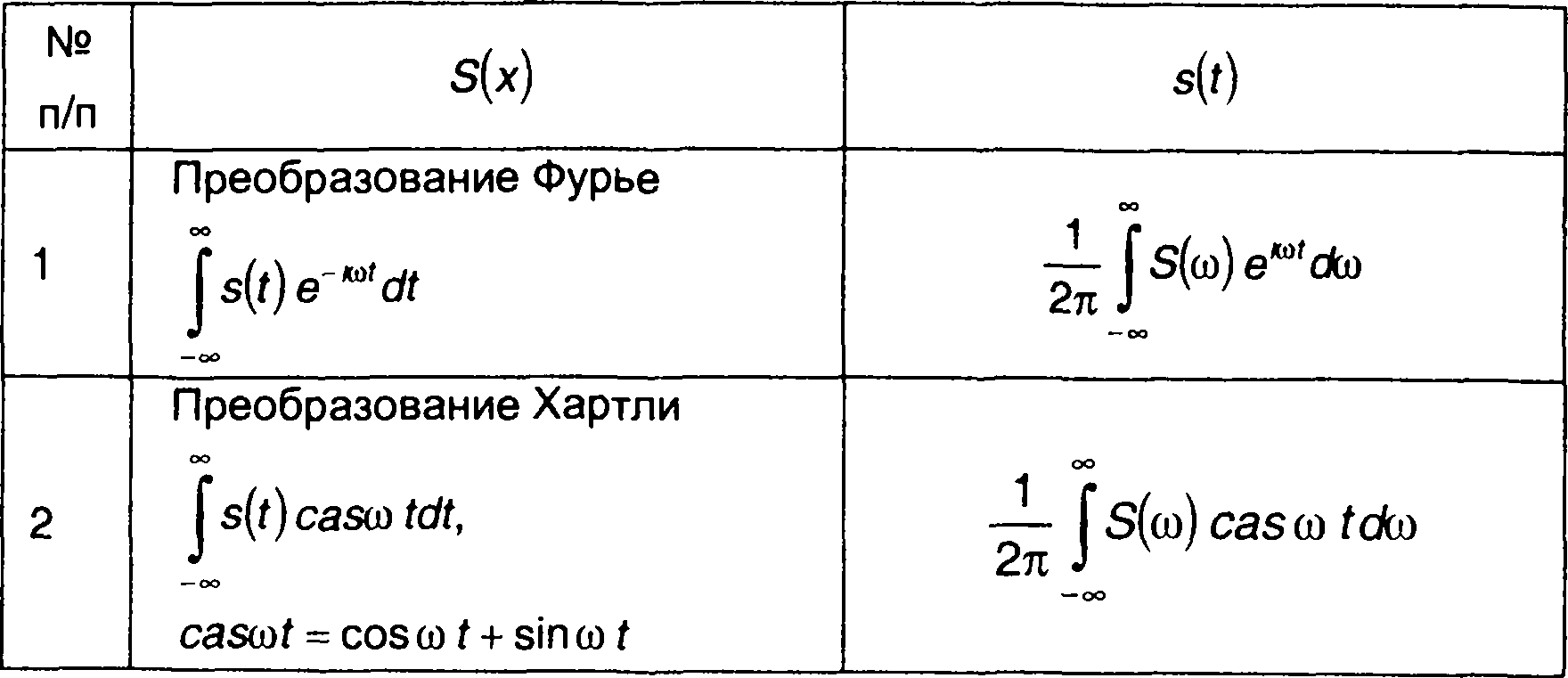
1.4. Векторное представление сигналов

При анализе сигналов часто обращаются к их геометрической интерпретации. Такой подход придает описанию сигналов большую образность, позволяет проводить исследования сигналов извест­ными методами многомерной геометрии.

Элемент X N- мерного пространства представляется как точка или вектор с координатами х₁, х₂, ..., x_N. Само пространство рас­сматривается как совокупность таких элементов или пространство векторов.

Если определено расстояние между двумя точками пространст­ва X(x₁, х₂, ..., x_N) и Y(y₁, у₂, ..., y_N), то пространство называется мет­рическим. Наиболее часто используется метрика, определяемая выражением

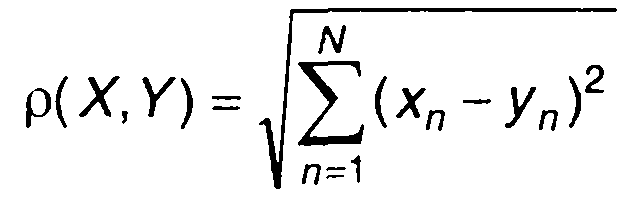(1.32)

Пространство с метрикой (1.32) называется N-мерным евклидо­вым пространством. Оно обычно и рассматривается при векторном представлении сигналов.

При геометрической интерпретации множеству сигналов ставит­ся в соответствие векторное пространство. Сигналы изображаются векторами, а операции с сигналами заменяются операциями с век­торами.

Сигнал, описываемый выражением

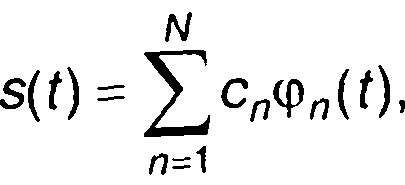(1.33)

s(t) и φ_n(t)

может рассматриваться как N-мерный вектор (рис. 1.9). Ортонормированная система базисных функций {φ_n(t)} образует коорди­натную систему в N-мерном евклидовом пространстве. Функции φ_n(t) представляют единичные векторы (орты), коэффициенты с_n - проекции вектора s(t) на оси координат.

Координаты вектора определяются скалярным произведением

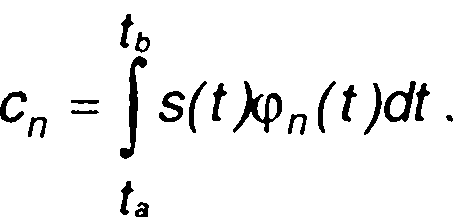(1.34)

Длина вектора определяется как

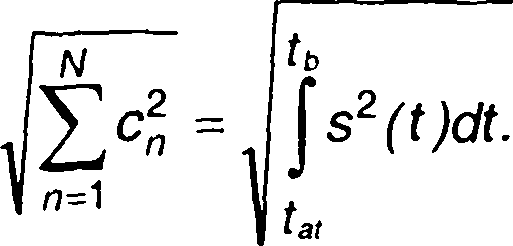(1.35)

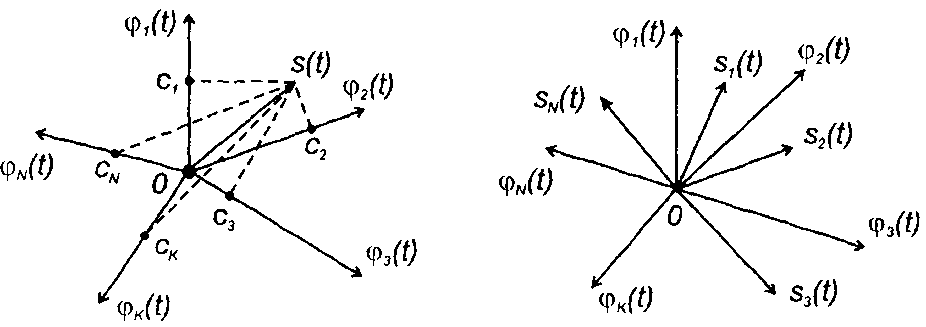
Рис. 1.9 Рис. 1.10

Векторы можно рассматривать лишь тогда, когда они имеют ко­нечную длину. Из (1.35) следует, что геометрическую интерпрета­цию допускают только сигналы с ограниченной энергией

Совокупность сигналов с ограниченной энергией образует про­странство сигналов (рис. 1.10). В нем сумме сигналов

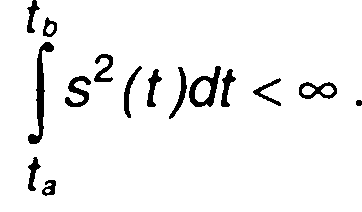(1.36)

соответствует сумма векторов. Если сигналы s₁(t) и S₂(t) заданы на интервале времени [t_a, t_b] в единой системе координат

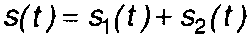(1.37)

то суммарный вектор s(t) определяется координатами с_1n + с_2п. Его длина равна

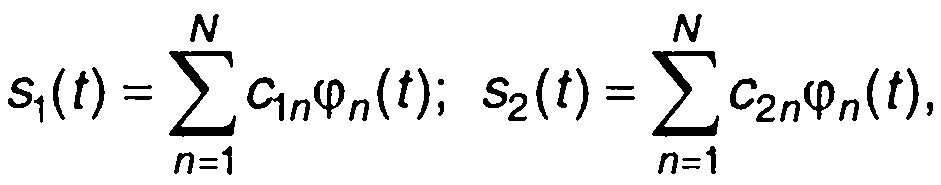(1.38)

Скалярное произведение двух векторов S₁(t) и S₂(t) определя­ется выражением

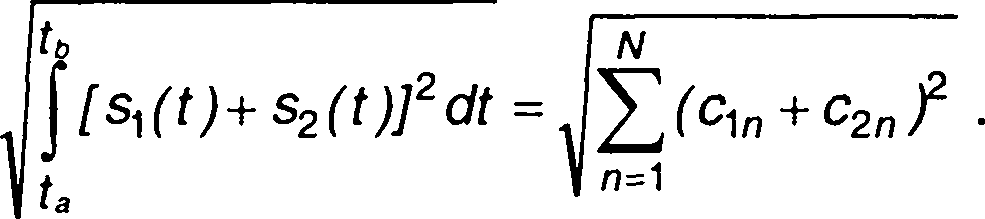(1.39)

Величина, описываемая (1.40), представляет взаимную энергию сигналов.

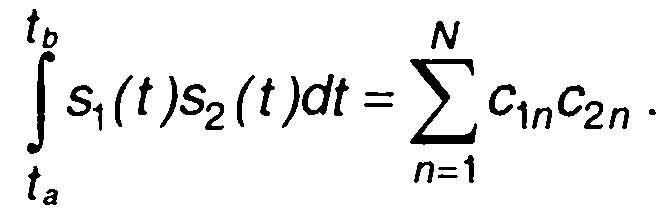(1.40)

Путем поворота системы координат относительно начала коор­динат можно получить бесчисленное множество координатных сис­тем. Замена координатной системы означает замену системы ба­зисных функций, используемых при разложении сигнала, изменяет­ся спектр сигнала. Свойства же векторов, отражающие свойства сигналов, остаются неизменными, в том числе длины векторов, расстояния и углы между векторами.

Все понятия /V-мерного евклидова пространства при обобщаются на бесконечномерное гильбертово пространство.

1.5. Энергия и мощность сигналов

Важнейшими характеристиками сигналов являются энергия и мощность. Энергия сигнала s(t) за интервал времени [t_а, t_ь] опреде­ляется выражением

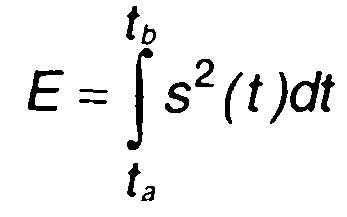(1.41)

Используя интегральное преобразование сигнала, выражение для энергии можно записать иначе. Так, вводя преобразование Фу­рье, получим

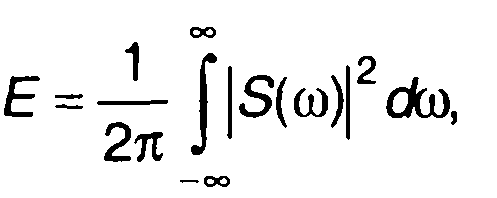(1.42)

где

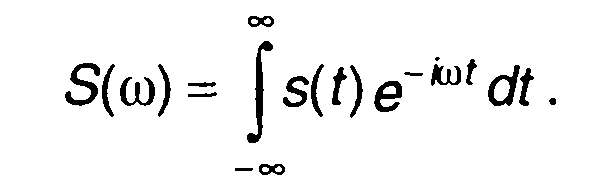(1.43)

Представление сигнала в виде тригонометрического ряда Фурье позволяет получить следующее выражение для энергии сигнала:

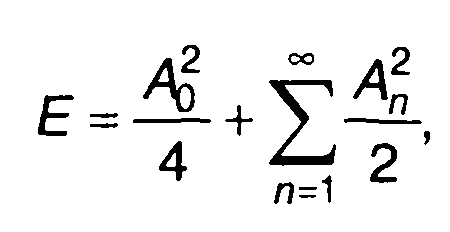(1.44)

где А_п — коэффициенты ряда Фурье.

Таким образом, можем записать

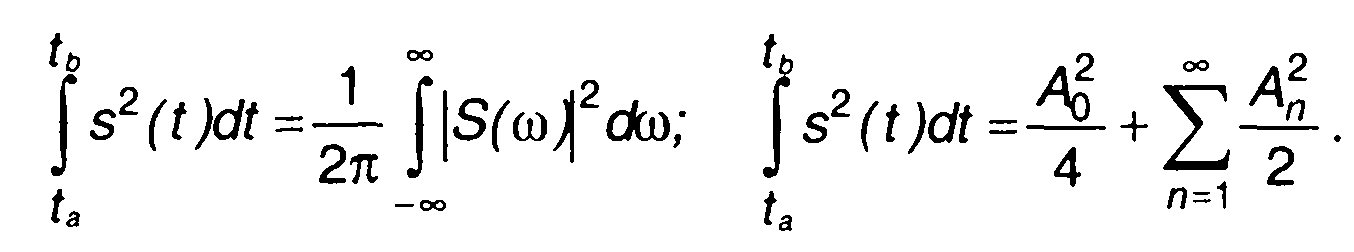(1.45)

Соотношения (1.45) представляют различные формы записи ра­венства Парсеваля, позволяют определить энергию сигнала, имея преобразование Фурье временной функции, описывающей сигнал, или ее представление в виде ряда Фурье.

Энергия суммы двух сигналов за интервал времени [t_a, t_b] равна

(1.46)

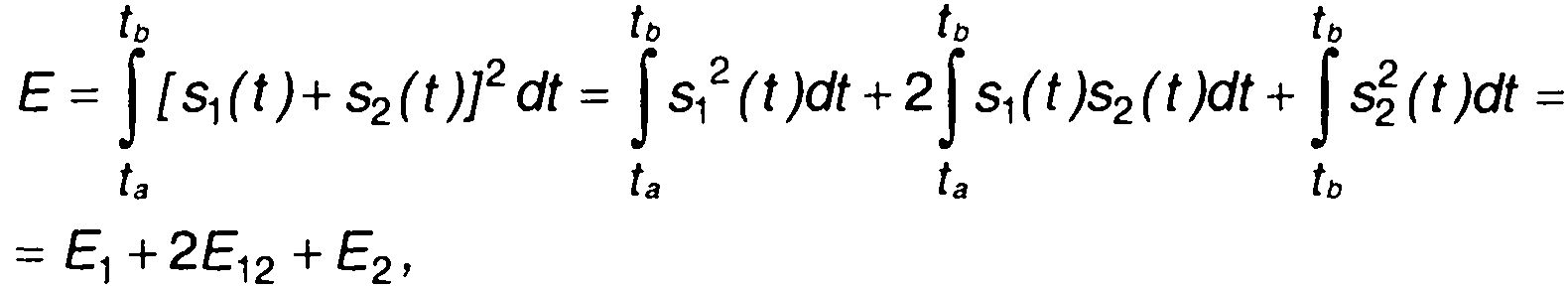
где E₁ , Е₂ - энергии сигналов s₂(t) и s₂(t); Е₁₂ - взаимная энергия двух сигналов.

Если сигналы ортогональны и выполняется условие

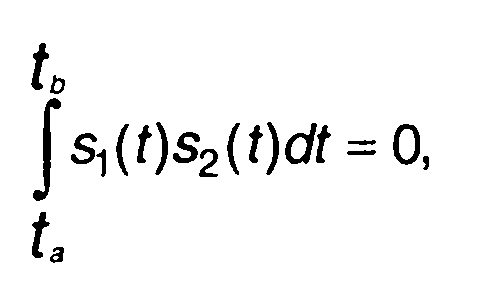(1.47)

то их энергии аддитивны:

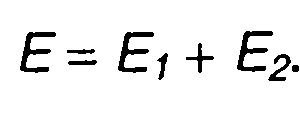(1.48)

Степень взаимозависимости двух сигналов в общем случае опи­сывается корреляционной функцией

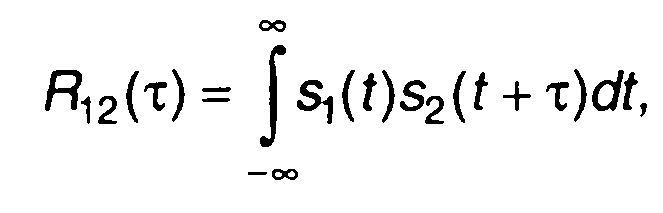(1.49)

где τ - смещение во времени одного сигнала относительно другого.

Выражение (1.49) записано для непериодических сигналов с ог­раниченной энергией. Подчеркивая то, что рассматриваются два сигнала, функцию R₁₂(τ) называют взаимной корреляционной

функцией. При τ = 0 взаимная корреляционная функция описывает взаимную энергию сигналов

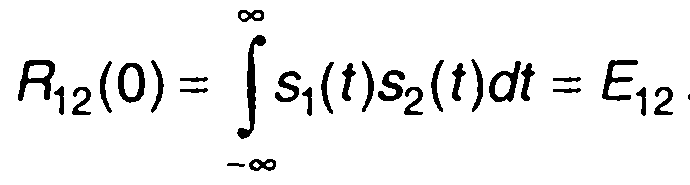(1.50)

С учетом (1.50) выражение (1.46) можем записать в виде

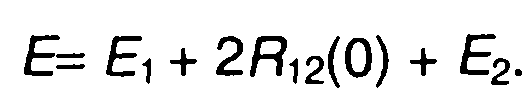(1.51)

Корреляционная функция может также характеризовать взаим­ную зависимость двух значений одного сигнала s(t), разнесенных во времени

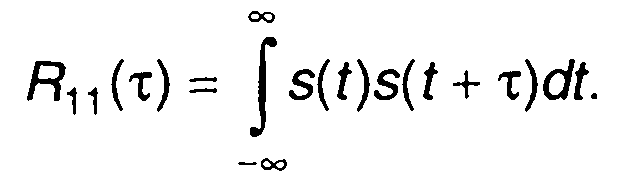(1.52)

В этом случае она называется автокорреляционной функцией.

При τ = 0

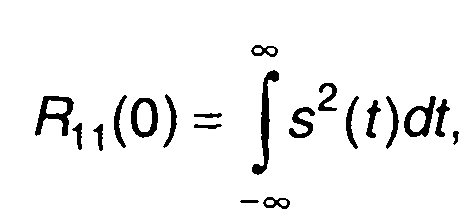(1.53)

автокорреляционная функция равна энергии сигнала.

Средняя мощность сигнала за интервал времени [t_a, t_b] опреде­ляется выражением

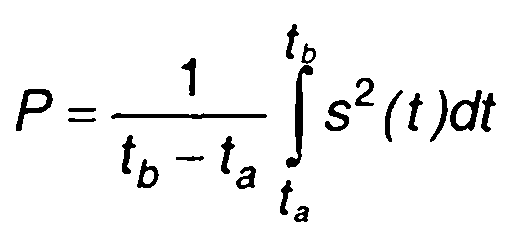(1.54)

Средняя мощность суммы двух сигналов за интервал времени [t_a, t_b] равна

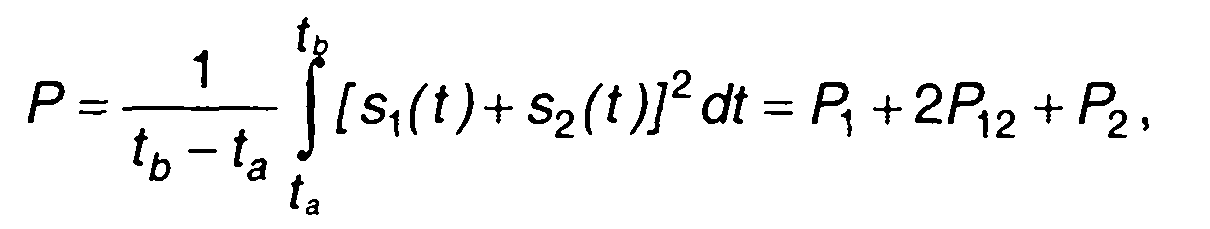(1.55)

где 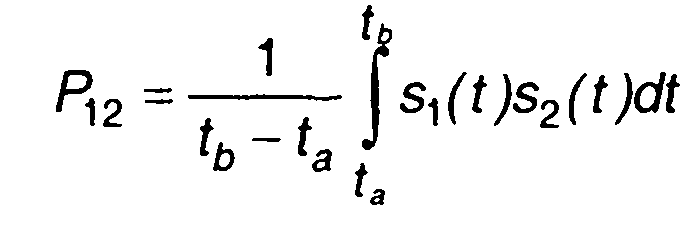- взаимная мощность.

Для периодического сигнала, имеющего период, равный Т, средняя мощность определяется выражением

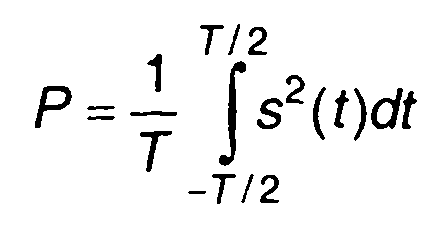(1.56)

Для двух периодических сигналов s₁(t) и s₂(t), имеющих один и тот же период Т, взаимная корреляционная функция описывается выражением

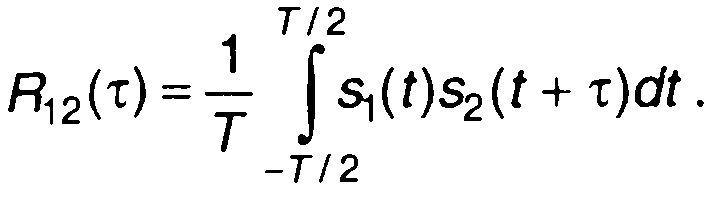(1.57)

При s,(t)=s2(t)=s(t) из (1.57) получим выражение для автокорре­ляционной функции периодического сигнала

Таким образом, автокорреляционная функция периодического сигнала при т = 0 описывает среднюю мощность сигнала.

Рассмотренные энергетические характеристики сигналов явля­ются основными, к ним приходится обращаться в дальнейшем при анализе различных видов сигналов.

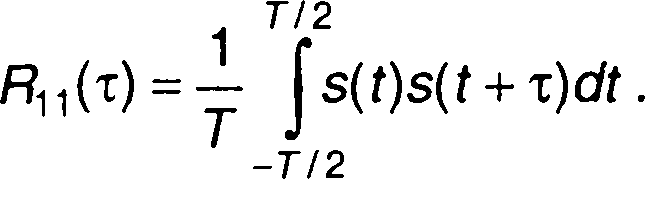(1.58)

При τ = 0 имеем

R₁₁(0) = P. (1.59)

1.6. Основные виды сигналов

Все возможное разнообразие сигналов можно свести к несколь­ким видам, которые составляют основу их классификации.

Одним из основных признаков, по которым различаются сигна­лы, является предсказуемость сигнала (его значений) во времени. Различают детерминированные и случайные сигналы. К детерми­нированным (регулярным) относят сигналы, которые описываются функциями времени, или для которых задано правило их получе­ния. Такими сигналами, например, являются периодические после­довательности импульсов определенной формы, высокочастотные колебания, модулированные по заданному закону, двоичные по­следовательности символов, формируемые заданным способом, и т. д. Значения детерминированного сигнала определены в каждый момент времени. К случайным сигналам относятся сигналы, значе­ния которых в любой момент времени невозможно предсказать с вероятностью, равной единице. К ним относятся высокочастотные колебания, модулированные шумом, колебание на входе приемни­ка, источником которого является космическое излучение, и др. Строго говоря, все сигналы, которые встречаются на практике, яв­ляются случайными. Даже при формировании сигнала определен­ного вида всегда имеются случайные изменения во времени его

параметров. Другие сигналы, такие как речевые, имеют случайный характер вследствие самого содержания передаваемой информа­ции. С этой точки зрения детерминированные сигналы представ­ляют только математическую модель реальных сигналов. Однако принятые модели часто достаточно хорошо описывают реальные сигналы (в первую очередь, когда флуктуации имеют малые значе­ния) и удобны при их анализе.