Система передачи информации

В системах автоматики и телемеханики, проводной и радиосвязи сигнал передается на более или менее далекое расстояние чаще всего в виде электромагнитного возмущения. Поэтому физической величиной, определяющей характер сигнала, обычно является напряжение (или ток), изменяющееся во времени по определенному закону, отображающему передаваемое сообщение. В теоретических исследованиях сигнал, независимо от его физической природы, заменяется математическим представлением в виде некоторой функции времени, описывающей закон изменения во времени, заложенный в реальном сигнале.

Сигнал будем называть регулярным, если его математическим представлением является заранее заданная функция времени f(t). Другими словами, регулярный сигнал соответствует известному сообщению.

Изучение свойств различного вида регулярных сигналов, связанных с их передачей, позволяет перейти к исследованию более сложных сигналов, имеющих характер случайных процессов.

Выражение регулярного сигнала определенной функцией времени называют временным представлением сигнала. Форма записи функции может быть различной. В частности, при некоторых ограничениях, функция времени, заданная на некотором отрезке времени, может быть представлена в виде тригонометрического ряда, каждый член которого является простейшей гармонической функцией времени (косинус, синус). Эти функции называются гармониками, и каждой из них принадлежат определенные амплитуда, частота и фаза. Множество амплитуд, частот и фаз называют спектром рассматриваемого сигнала. Функция времени находится в однозначном соответствии с принадлежащим ей спектром. На этом основании временное представление сигнала может быть заменено так называемым частотным представлением. Оба представления адекватны. Выбор того или иного представления зависит от физических и математических особенностей рассматриваемой задачи.

К основным типам регулярных сигналов относятся: периодический, почти периодический и непериодический.

Периодический сигнал представляется функцией времени, удовлетворяющей условию

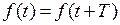, (1.1)

где t – любой момент времени на интервале -¥ £ t£+¥ , а T – некоторая постоянная.

Наименьший конечный промежуток времени Т, удовлетворяющий условию (1.1), называется периодом.

Периодический сигнал физически неосуществим, так как реальный сигнал не может продолжаться вечно; он всегда имеет начало и конец. Однако абстрактный смысл периодического сигнала не мешает его широкому использованию в теоретических исследованиях и получению результатов, соответствующих наблюдаемым в действительности. Дело в том, что регулярный сигнал, воздействующий на какое-либо устройство, можно считать существовавшим бесконечно долго, если рассматривается только установившийся режим, который не зависит от начальных условий.

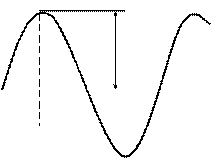
Простейшим и наиболее распространенным периодическим сигналом является гармонический сигнал (рис. 1.1), выраженный косинусоидальной (или синусоидальной) функцией времени.

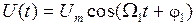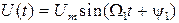, или , (1.2)

где U(t)– мгновенное значение напряжения; U_m – его амплитуда; W₁= 2p/T – угловая частота; T – период; y₁ – начальная фаза; j₁ = y₁–90°.

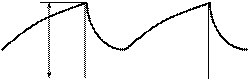
На рис. 1.2 показан график периодического несинусоидального напряжения, которое получается при непрерывно повторяющейся зарядке конденсатора от источника напряжения U₀и его разрядке через активное сопротивление.

		W1t

Функция, описывающая данный процесс, имеет вид

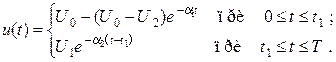(1.3)

Коэффициенты a₁ и a₂ показывают скорость зарядки и разрядки и зависят от емкости конденсатора и величин активных сопротивлений цепей зарядки и разрядки.

В общем виде это напряжение, как и другие периодические функции f(t), можно записать так:

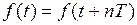, (1.4)

где n – любое целое положительное или отрицательное число; T – период.

В математике функция, представляемая в виде суммы гармонических составляющих с произвольными частотами, получила название почти периодической функции. Почти периодические функции обладают многими замечательными свойствами, и их исследованиям отведено большое место в современной теории функций. Одно из основных свойств заключается в том, что для данных функций может быть определен приближенный период (почти-период). В системах телемеханики встречаются сигналы, частоты гармоник которых не находятся в простых кратных соотношениях. Подобные сигналы называют почти периодическими.

Непериодическим называется регулярный сигнал, определяемый непериодической функцией, т.е. функцией, которая не удовлетворяет условию (1.1) на всем интервале времени -¥ £ t £ +¥. Такой сигнал представляется функцией, заданной в пределах конечного (t₁ £ t £ t₂) или полубесконечного (t₁ £ t < ¥) промежутка времени, вне которого она принимается тождественно равной нулю. Форма сигнала может быть практически любой и, в частности, обладать периодичностью в пределах времени своего существования (например, конечный или полубесконечный отрезок синусоиды).

В зависимости от структуры информационных параметров различают сигналы:

1) непрерывные по множеству и времени, или просто непрерывные (рис. 1.3, а);

2) дискретные по множеству и времени, или просто дискретные (рис. 1.3, б);

3) непрерывные по времени и дискретные по множеству (рис. 1.3, в);

4) непрерывные по множеству и дискретные по времени (рис. 1.3, г).

а б

Рис. 1.3. Виды сигналов в системах телемеханики