Вопрос. Прямое преобразование (переход от сигнала к спектру).

Разложение в ряд Фурье позволяет получить спектр только для периодических сигналов. Преобразование Фурье расширяет область применения спектрального анализа на непериодические сигналы.

Пусть s(t) – одиночный импульсный сигнал конечной длительности. Дополним его таким же, периодически следующим сигналом, с периодом Т. Получим последовательность импульсов (рис.15).

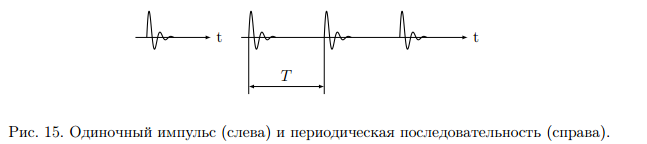
Чтобы перейти к преобразованию Фурье и найти спектр одиночного импульса необходимо найти предельный вид ряда Фурье в комплексной форме при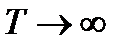

Расчет спектра:

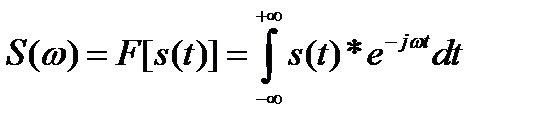
Физический смыл спектральной плотности состоит в том, что она является коэффициентом пропорциональности между длинной малого интервала частот Δf в близи частоты f₀ и амплитуды гармонического сигнала с частотой f₀. Сигнал s(t) как бы складывается из множества разных синусоидальных сигналов малой амплитуды. Спектр плотности показывает вклад в сигнал элементарных синусоидальных сигналов каждой частоты.

Спектр плотности вероятности 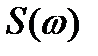является комплексным числом и отображается кривой на комплексной плоскости.

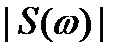- действительное число – амплитудный спектр

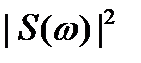- спектр мощности

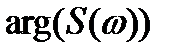- фазовый спектр