Спектральный анализ интегрируемых сигналов.
Сигнал 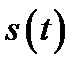 можно сопоставить спектральную плотность
можно сопоставить спектральную плотность 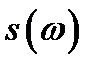 если сигнал абсолютно интегрирован.
если сигнал абсолютно интегрирован.
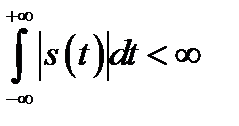
К абсолютно интегрированному сигналу не относятся гармонические колебания и постоянный ток.
Примеры абсолютно интегрируемых и неинтегрируемых сигналов на (рис. 16).

Спектры таких сигналов представляются через дельта-функции.
Спектр сигнала постоянного уровня А представляет собой дельта-импульс, расположенный на нулевой частоте ( 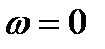 ).
).
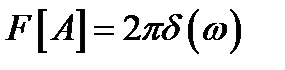
Физический смысл данного выражения – сигнал, постоянный по модулю и по времени имеет постоянную составляющую только на нулевой частоте.
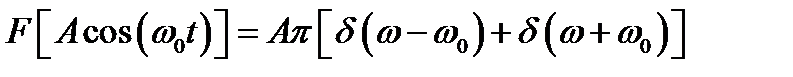 - спектр синусоидального сигнала.
- спектр синусоидального сигнала.
Любой периодический сигнал можно представить рядом Фурье в комплексной форме, то есть в виде суммы синусоидальных сигналов.
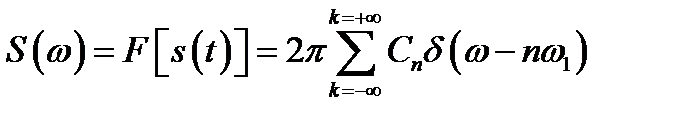
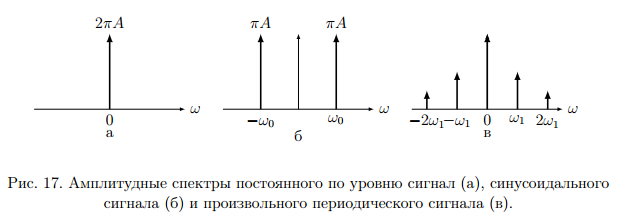
Спектры постоянного тока, синусоидального и периодического сигнала показаны на (рис. 17).
На анализаторе спектра спектр периодического сигнала будет наблюдаться в виде последовательности остроконечных импульсов. Амплитуды данных импульсов пропорциональны амплитудам гармоник. Типичный вид спектра представлен на (рис. 18).

Спектральный анализ можно применять и к случайным сигналам. Для них рассматривается спектр мощности 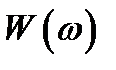 . Для примера рассмотрим белый шум (рис. 1).
. Для примера рассмотрим белый шум (рис. 1).

Белый шум имеет равномерный спектр, то есть выполняется условие 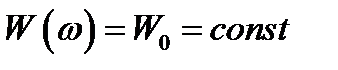 .
.
Дата добавления: 2015-12-29; просмотров: 1685;
