Свойства преобразования Фурье

1. Линейность – спектр суммы нескольких сигналов умножить на постоянные коэффициенты равен сумме этих сигналов. Если амплитуда сигнала меняется в А раз, то его спектральная плотность тоже меняется в А раз.

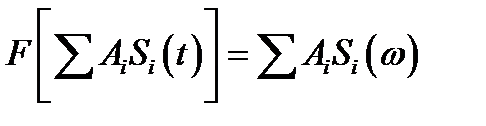
2. Свойство вещественной и мнимой частей спектра. Вещественная часть спектра, то есть амплитудный спектр – четный функция частоты. Амплитудный спектр симметричен относительно нулевой частоты. Мнимая часть спектра – нечетная функция частоты. Фазовый спектр антисимметричен относительно нулевой частоты.

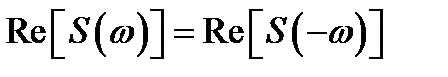
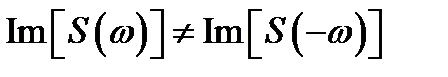
3. Смещение сигнала во времени. При смещении сигнала во времени амплитудный спектр не меняется, а фазовый спектр смещается по фазе.

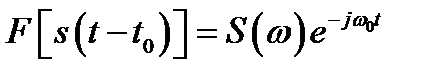
4. Изменение масштаба сигнала по времени. Пусть сигнал s(t) сжат по времени в k-раз. Сжатый сигнал записывается, как s(kt).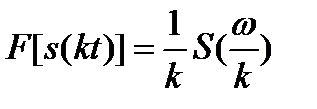

5. Свертка и произведение двух сигналов.

Спектр произведения сигналов равен свертке спектров и наоборот.

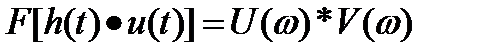
Свойство применяется для отыскания сигнала на выходе, если известна АЧХ.

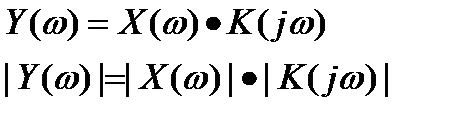
Линейная система и сигналы на ее входе и выходе показаны на рисунке 20.

6. Спектр дельта функции.

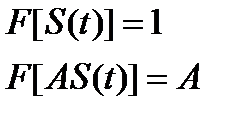
В спектре дельта-импульса содержатся все частоты от 0 до .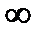

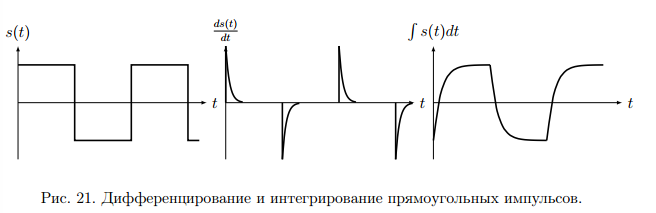
7. Спектр производной и интеграла.

Дифференциация сигналов приведет к расширению спектра, интегрирование – к сжатию (рис.21).

8. Связь с рядами Фурье.

Комплексная амплитуда 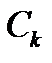к-ой гармоники ряда Фурье связана со спектральной плотностью так: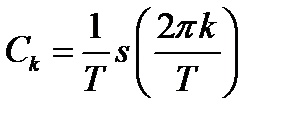

Зная преобразование для одного периода периодического сигнала можно вычислить его разложение в ряд Фурье.