Бесконечно малые и бесконечно большие функции.
Определение 1. Функция f(x) называется бесконечно большойфункцией при х →x0, если 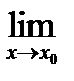 f(x) =
f(x) = 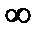 .
.
Определение 2. Функцияf(x) называется бесконечно малой функцией при х →x0, если 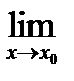 f(x) = 0.
f(x) = 0.
Основные теоремы о пределах функций.
Теорема 1.Предел постоянной величины равен самой постоянной:
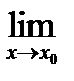 c = c.
c = c.
Теорема 2.Пределсуммы (разности) двух функций равен сумме (разности) их пределов:
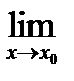
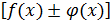 =
= 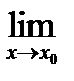 f(x)
f(x) 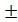
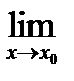 φ(x).
φ(x).
Теорема 3.Пределпроизведения двух функций равен произведению их пределов:
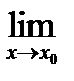
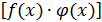 =
= 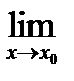 f(x)
f(x) 
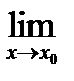 φ(x).
φ(x).
Теорема 4.Предел дроби равен пределу числителя, деленному на передел знаменателя, если предел знаменателя не равен нулю:
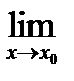
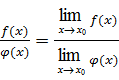 ,
, 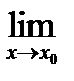
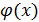 ¹ 0.
¹ 0.
Теорема 5.(О пределе промежуточной функции) Если в окрестности точки x0выполняются неравенства:
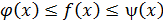 и
и 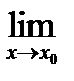
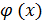 =
= 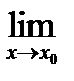
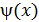 = А, то
= А, то 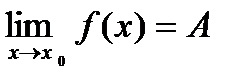 .
.
Лекция 5.ТЕХНИКА ВЫЧЕСЛЕНИЯ ПРЕДЕЛОВ
Замечательные приделы.
Пример 1.
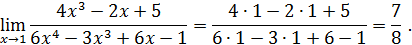
Будем говорить, что предел отношения двух функций 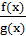 есть неопределенность вида
есть неопределенность вида  или
или  , если числитель и знаменатель дроби одновременностремятся к нулю или к бесконечности. Раскрыть эти неопределенности – значит вычислить предел отношения
, если числитель и знаменатель дроби одновременностремятся к нулю или к бесконечности. Раскрыть эти неопределенности – значит вычислить предел отношения 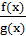 , если он существует или установить, что этот предел не существует.
, если он существует или установить, что этот предел не существует.
Пример 2.
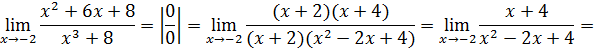
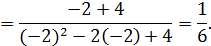
Из рассмотренного примера следует правило: чтобы раскрыть неопределенность вида  при x→x0 функции, заданной в виде отношения двух многочленов, необходимо в числителе и знаменателе выделить множитель x−x0 и дробь на него сократить.
при x→x0 функции, заданной в виде отношения двух многочленов, необходимо в числителе и знаменателе выделить множитель x−x0 и дробь на него сократить.
При вычислении пределов отношения двух многочленов при x→ 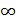 для раскрытия неопределенности вида
для раскрытия неопределенности вида  надо числитель и знаменатель дроби разделить на x в старшей степени.
надо числитель и знаменатель дроби разделить на x в старшей степени.
Пример 3.
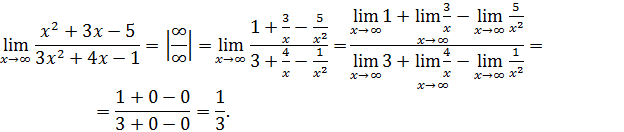
Пример 4.
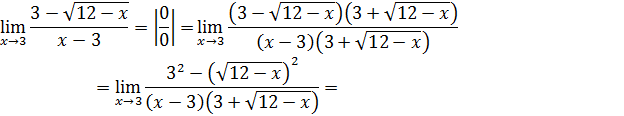
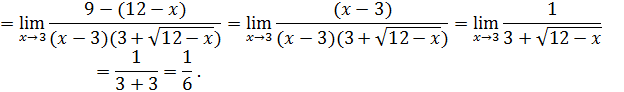
Дата добавления: 2015-12-16; просмотров: 1368;
