Числовые последовательности. Пределчисловойпоследовательности.
Пусть каждому натуральному числу nпоставлено в соответствие действительное число xп. Тогда говорят, что задана последовательность чисел x1, x2, x3, …, xn, … .
Числа x1, x2, x3, …, xn, будем называть элементами (или членами)последовательности, xn–общимчленомпоследовательности. Сокращенно последовательность обозначается 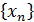 .
.
Например:
1) 1, 3, 5, …, 2n – 1 – арифметическая прогрессия.
d = 2;xn= 2n – 1; x100 = 2 ·100 – 1 = 199.
d =x2 – x1 = x3– x2 = … – разность прогрессии.
2) 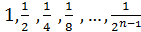 – геометрическая прогрессия.
– геометрическая прогрессия.
q= 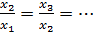 – знаменатель прогрессии.
– знаменатель прогрессии.
x5= 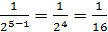 ;
;
3) 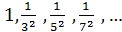
xn= 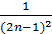 ;
;
Определение 1.Последовательность {xn} называется ограниченной, если она ограничена и сверху и снизу, то есть существуют числа mиMтакие, что любой элемент этой последовательности удовлетворяет неравенствам:
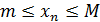
Пример:
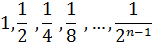
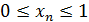
В противном случаи последовательность {xn} называется неограниченной.
Пример:
1, 2, 3, …, n – неограниченная последовательность.
Определение 2.Числоa называется пределом числовой последовательности {xn}, если для любого сколь угодно малого ε> 0найдетсячисло N (номер), зависящее от ε, такое, что для всех натуральных чисел n>Nвыполняется неравенство:
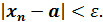
Тогда последовательность {xn} называется сходящейся,и в этом случае пишут:
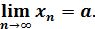
Пример:
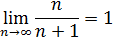
Для любого 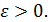
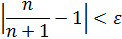
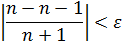
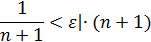
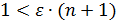
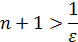
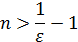
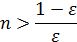
Так как 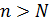 , то
, то 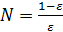
Пусть 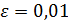 , тогда
, тогда 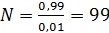 .
.
Следовательно 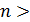 99.
99.
Например:
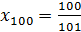 , тогда
, тогда 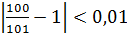 .
.
Дата добавления: 2015-12-16; просмотров: 1391;
