Лекция 12. УСЛОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ. УСЛОВНЫЕ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДВУМЕРНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН. РЕГРЕССИЯ.

Две случайные величины X и Y называются независимыми, если закон распределения одной из них не зависят от того, какие значения примет вторая величина.

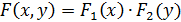
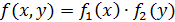
Условным знаком распределения одной из одномерных составляющих двумерной случайной величины называется её закон распределения, составленный при условии, что вторая составляющая приняла определенное значение или попала в определенный интервал.

Вероятности этого распределения называются условными вероятностями.

Для дискретной случайной величины:

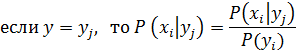
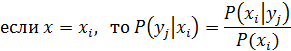
Для непрерывной случайной величины вероятности заменяются на плотности вероятностей:

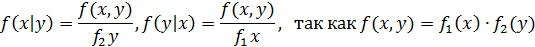
Условным математическим ожиданием дискретной случайной величины Y при X=x называется сумма произведений всех возможных значений этой величины на их условные вероятности:

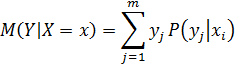
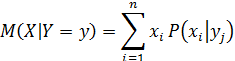
Условное математическое ожидание является функциями, которые называются функциями регрессии.

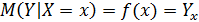
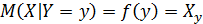
Графики этих функций называются линиями регрессии.