Генеральная выборочная и исправленная дисперсия.
Генеральной дисперсией 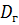 называется среднее арифметическое квадратов отклонений значений признака
называется среднее арифметическое квадратов отклонений значений признака 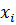 отих генеральной средней:
отих генеральной средней:
1. Если значения признака различны, то
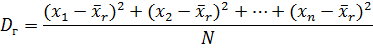
2. Если значения признака имеют частоты, то
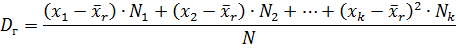
или
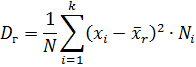
Выборочная дисперсия ‒ среднее арифметическое квадратов отклонений значений признака от их выборочной средней.
1. Если значения признака различны, то
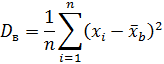
2. Если значения признака имеют частота, то
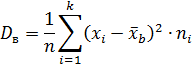
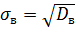
Пример.
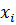
| ||||
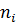
|
Найти: 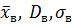 .
.
Решение:
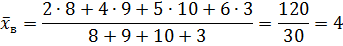
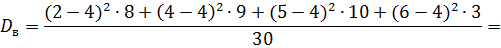
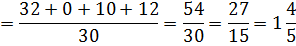
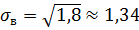
Для вычисления дисперсии используют еще одну формулу.
Дисперсия (любая) равна разности среднего арифметического квадратов значений признака и квадрата общей средней:
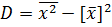
Пример.
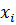
| ||||
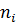
|
Решение:
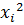
| ||||
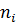
|
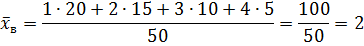
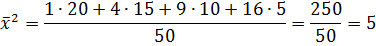
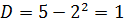
Выборочная дисперсия при выборках малого объема имеет систематическую ошибку, чтобы ее избежать, дисперсию умножают на число
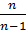 .
.
Полученная дисперсия называется исправленной дисперсией и обозначается 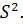
Итак,
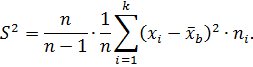
Следовательно,
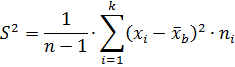
Тогда 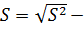 исправленное среднее квадратическое отклонение.
исправленное среднее квадратическое отклонение.
При 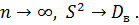
Дата добавления: 2015-12-16; просмотров: 1867;
