Оценки математического ожидания и среднего квадратического отклонения нормально распределенного признака.
1. Для оценки математического ожидания М (Х) = а нормально распределенного признака по выборочной средней и известному среднему квадратическому отклонению 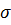 служит следующий доверительный интервал:
служит следующий доверительный интервал:
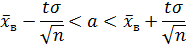
где 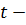 значение аргумента интегральной функции Лапласа (в таблице № 2).
значение аргумента интегральной функции Лапласа (в таблице № 2).

2. При исправленном среднем квадратическом отклонении S получим:

где 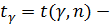 значения в таблице № 3.
значения в таблице № 3.
3. Доверительный интервал для оценки среднего квадратического отклонения 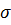 при большом числе измерений
при большом числе измерений  имеет вид:
имеет вид:

при 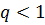
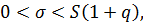
при 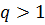
где 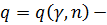 значения в таблице № 4.
значения в таблице № 4.
Пример 1.
Задана выборка значений признака X, имеющего нормальное распределение:
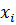
| ‒2 | |||||
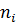
|
Найти: а) выборочную среднюю 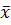 и исправленное среднее квадратическое отклонение s; б) указать доверительный интервал, покрывающий с надежностью 0,95 неизвестное математическое ожиданиеа признака X; в) указать доверительный интервал, покрывающий с надежностью 0,95 среднее квадратическое отклонение
и исправленное среднее квадратическое отклонение s; б) указать доверительный интервал, покрывающий с надежностью 0,95 неизвестное математическое ожиданиеа признака X; в) указать доверительный интервал, покрывающий с надежностью 0,95 среднее квадратическое отклонение 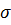 признака X.
признака X.
Решение:
а) Вычисляем объем выборки: 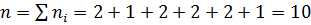 .
.
Тогда
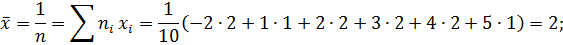
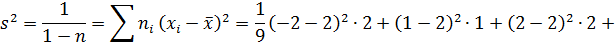

б) Искомый доверительный интервал для математического ожиданияа имеет вид:
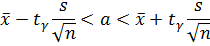
где 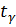 находим по таблице приложения 2. При
находим по таблице приложения 2. При  = 0,95 n = 10 получаем
= 0,95 n = 10 получаем 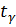 = 2,26. Тогда
= 2,26. Тогда
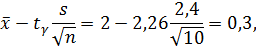
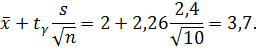
Таким образом,
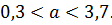
в) Доверительный интервал для генерального среднего квадратического отклоненияа имеет вид:
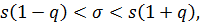 если
если 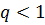
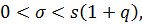 если
если 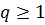
Соответствующие значения q указаны в таблице приложения 3. По заданным 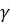 = 0,95 и n = 10 находим q = 0,65. Теперь искомый доверительный интервал запишется следующим образом:
= 0,95 и n = 10 находим q = 0,65. Теперь искомый доверительный интервал запишется следующим образом:

или
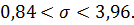
Дата добавления: 2015-12-16; просмотров: 1314;
