Лекция 11. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ (СЛУЧАЙНЫЕ ВЕКТОРЫ). ЗАКОН РАСПРЕДЕЛЕНИЯМНОГОМЕРНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.
До сих пор рассматривались случайные величины, возможные значения которых, определялись одним числом. Такие случайные величины называются одномерными.
Выпадение определенного числа очков при подбрасывании игральных костей, являются примером одномерной дискретной случайной величины.
На практике встречаются случайные величины, значение которых определяется двумя, тремя и более числами. Такие случайные величины называются многомерными.
Например:
Координаты точки, брошенной на плоскость, являются двумерной случайной величиной.
Упорядоченную пару чисел(Х,Y) случайных величин(Х и Y) назовем двумерной случайной величиной или случайным вектором. Геометрически она представляет собой точку на координатной плоскости.
Двумерные случайные величины делятся на дискретные и непрерывные.
Определение.Законом распределения дискретной двумерной случайной величины называется соответствие между возможными значениями ( 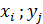 ) этой случайной величины и их вероятностями (
) этой случайной величины и их вероятностями ( 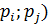 ,
,
где 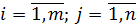
Закон распределения дискретной двумерной случайной величины (X, Y) имеет вид:

| 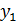
| 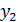
| … | 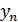
|
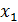
| 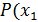 ; ; 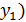
| P( 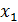 ; ; 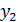 ) )
| … | 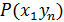
|
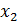
| 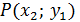
| P( 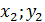 ) )
| … | P 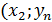 ) )
|
| … | … | … | … | … |
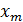
| P( 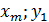 ) )
| P( 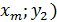
| … | Р( 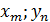 ) )
|
Сумма вероятностей равна единице, то есть
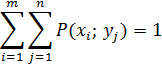
Дата добавления: 2015-12-16; просмотров: 1423;
