Асимметрия и эксцесс.

В прикладных задачах, например в математической ста­тистике, при теоретическом изучении эмпирических распре­делений, отличающихся от нормального распределения, воз­никает необходимость количественных оценок этих различий. Для этой цели введены специальные безразмерные характеристики.

Определение. Асимметрией теоретического распределения называется отношение центрального момента третьего поряд­ка к кубу среднего квадратического отклонения:

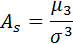
Определение. Эксцессом теоретического распределения на­зывается величина, определяемая равенством:

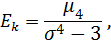
где 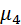‒ центральный момент четвертого порядка.

Для нормального распределения 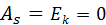. При отклоне­нии от нормального распределения асимметрия положительна, если "длинная" и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствую­щей моде; если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рис. 1, а, б).

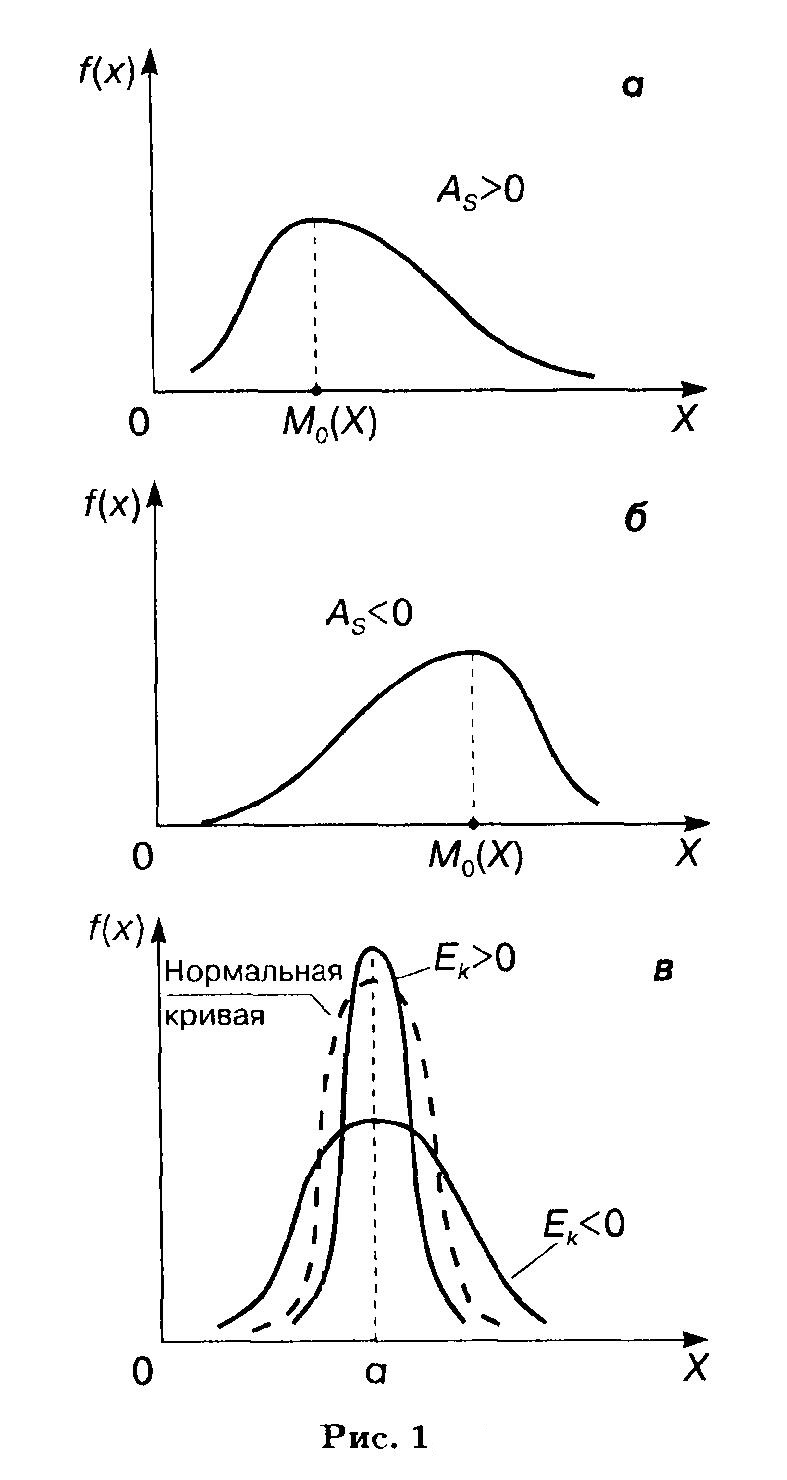
Эксцесс характеризует "крутизну" подъема кривой распре­деления по сравнению с нормальной кривой: если эксцесс поло­жителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину.

Следует иметь в виду, что при использовании указанных характеристик сравнения опорными являются предположения об одинаковых величинах математического ожидания и дис­персии для нормального и теоретического распределений.

Пример. Пусть дискретная случайная величина Х задана законом распределения:

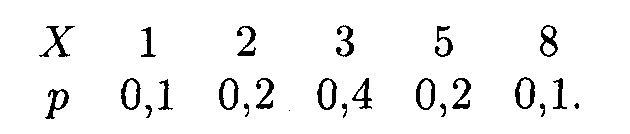
Найти: асимметрию и эксцесс теоретического распределения.

Решение:

Найдем сначала математическое ожидание слу­чайной величины:

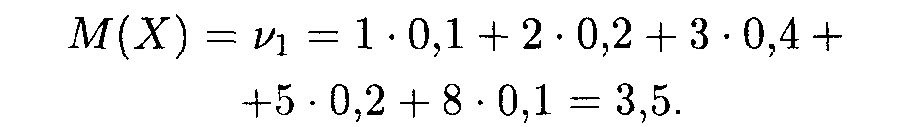
Затем вычисляем начальные и центральные моменты 2, 3 и 4-го порядков и среднее квадратическое отклонение:

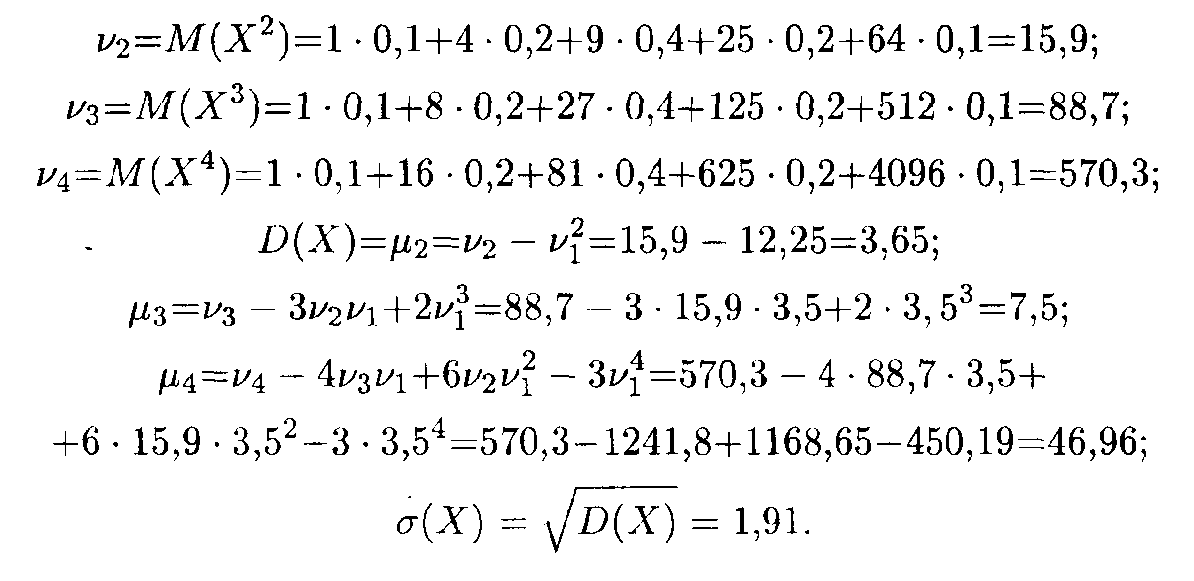
Теперь по формулам находим искомые вели­чины:

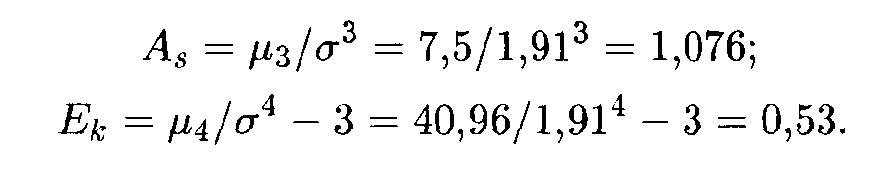
В данном случае "длинная" часть кривой распределения рас­положена справа от моды, причем сама кривая является не­сколько более островершинной, чем нормальная кривая с теми же величинами математического ожидания и дисперсии.