Лекция 10. ВЕРОЯТНОСТЬ ПОПАДАНИЯ В ИНТЕРВАЛ. ПРАВИЛО ТРЕХ СИГМ. НЕРАВЕНСТВО ЧЕБЫШЕВА. ЗАКОН БОЛЬШИХ ЧИСЕЛ. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА.

Теорема.Вероятность отклонения непрерывной случайной величины от её математического ожидания на величину сколь угодно малого числа ε>0 находится по формуле:

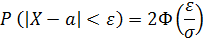
Доказательство:

Так как

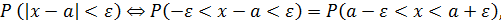
то

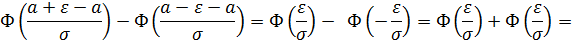
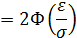
Следовательно,

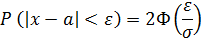
Правило 3 ‒ х сигм.

Пусть .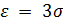

Подставим значение ε в формулу, получим:

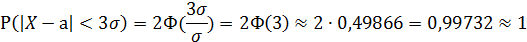
Вывод:

Итак, с вероятностью сколь угодно близкой к единице можно утверждать, что модуль отклонения нормально распределенной случайной величины от её математического ожидания не превосходит утроенного среднего квадратического отклонения.

Центральная предельная теорема.

Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.

Теорема Ляпунова.

Если случайная величина Х представляет собой сумму большого числа взаимно ‒ независимых случайных величин, то есть 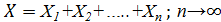, влияние каждой из которых на всю сумму ничтожно мало, то случайная величина Х имеет распределение, не ограниченно приближающееся к нормальному распределению.