II ЗАКОН ТЕРМОДИНАМИКИ
Все многообразные процессы, происходящие в окружающем нас мире — в природе, в производственных и других условиях, — можно разделить на три групп:
| Процессы | ||
| Несамопроизвольные | Равновесные | Самопроизвольные |
| - это процессы, для совершения которых требуется затраты работы извне, в количестве, прямо пропорциональном производимого изменению. | - процессы, для течения которых не требуется затраты работы извне и в результате которых не может быть получена работа против внешних сил. | -процессы, которые не требуют затраты работы извне, причем в результате их может быть получена работа против внешних сил в количестве, пропорциональном происшедшему изменению. |
Процессы также делятся на обратимые и необратимые:
Обратимые — это процессы, в результате которых можно вернуть в систему первоначальное состояние без изменений в окружающей среде.
Необратимые — это процессы, в результате которых систему можно вернуть в исходное состояние, лишь произведя изменения в окружающей среде.
Все самопроизвольные процессы необратимые. Работа обратимого процесса max и всегда больше работы необратимого процесса.

ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Второй закон термодинамики, как и первый, является постулатом. Приведем некоторые наиболее часто встречающиеся формулировки:
1. Постулат. Теплота не может переходить самопроизвольно от менее нагретого к более нагретому телу.
2. Постулат (Томсона и Кельвина). Не могут осуществляться процессы, единственным результатом которых был бы переход теплоту в работу.
3. Постулат. Невозможен вечный двигатель второго рода.
Работа считается положительной, если она производится над системой, а термодинамическая теплота считается положительной, если дается телу.
С помощью второго закона термодинамики мы можем ответить на три вопроса:
1. Возможность протекания самопроизвольного процесса (Т1≠Т2). Если в системе имеется две области с разными температурами, то возможно протекания самопроизвольного процесса.
2. Направление протекания самопроизвольного процесса (Т1˃→Т2˂). Здесь учитывая формулировку второго закона термодинамики, можно сказать, что процесс идет в направлении от более нагретого тела к менее нагретому.
3. Предел протекания самопроизвольного процесса (Т1 = Т2). Процесс будет протекать до тех пор, пока в системе не установится одинаковая температура, т.е. пока система не достигнет равновесия.
Таким образом, второй закон дает возможность определить, какими должны быть внешние условия, чтобы интересующий нас процесс мог происходить в нужном нам направлении и в требуемой степени. Такая возможность имеет очень большие значение как для исследования теоретических проблем физической химии, так и для решения различных задач прикладного характера.
Второй закон термодинамики носит статистический характер, и применим лишь к системам из большого числа частиц, т.е. таким, поведение которых может быть выражено законами статистики.
Определение характеристик процесса может быть осуществлено двумя методами:
А) С помощью факторов интенсивности (T,P,N, μ и др);
Б) С помощью характеристических функций.
Таким образом, ответить на вопрос о возможности, направлении и пределе протекания самопроизвольных процессов можно следующим образом:
1. Возможностью протекания самопроизвольного процесса определяется неравенством факторов интенсивности в различных частях системы;
2. Самопроизвольный процесс протекает из области с большим фактором интенсивности в область с меньшим фактором;
3. Всякий самопроизвольный процесс стремится к выравниванию факторов интенсивности.
Этот метод не применим к системам однородным или вообще к процессам, протекание которых не вызывает неоднородности системы (н-р, гомогенные химические реакции). Поэтому используют более общий второй метод (Б).
Второй метод (Б) основан на следующем положении, вытекающем из второго закона термодинамики:
Для процессов, протекающих при различных условиях, есть своя собственная функция, по изменению которой можно судить о возможности, направлению и приделу протекания самопроизвольного процесса. Существует несколько таких функций , которые можно свести в таблицу.
| Функция | Название | Условия протекания самопроизвольных процессов | Изменение |
| S | энтропия | Изолированная система(Q=0) | ∆S˃0 |
| G | энергия Гиббса | P=const T= const | ∆G˂0 |
| F | Энергия Гельмгольца | V=const T= const | ∆F˂0 |
| H | энтальпия | P=const S=const | ∆H˂0 |
| U | внутренняя энергия | V=const S=const | ∆U˂0 |
ЭНТРОПИЯ
Энтропия (означается буквой S) — мера беспорядка системы. Чем больше беспорядка, тем больше энтропия.
Известно, что наименьшей энтропией обладают кристаллические (т.е. твердые) веществ; чуть большей энтропией обладают жидкости; самая большая энтропия у газообразных веществ. Sтв.˂Sж.˂Sгаз(пар) , [Дж/(моль*К]
ЭНТРОПИЯ И ТЕРМОДИНАМИЧЕСКАЯ ВЕРОЯТНОСТЬ
Термодинамическая вероятность W — это число микросостояний, которыми реализуется данная микросостояние.
Термодинамическая вероятность (в отличие от математической вероятности) выражается большим числом.
Для идеальных газов состояние наиболее вероятным является состояние с наиболее беспорядочным (хаотическим) расположением молекул. Этому состоянию отвечает наибольшее состояние энтропии S. Энтропия является функцией термодинамической вероятности системы S= f(W), где W— термодинамическая вероятность.
Термодинамическая вероятность обладает свойством мультипликативности, т.е. термодинамическая вероятность системы в целом равна произведению вероятностей:
Wсист.= W1+ W2+ W3+…+ Wn.
Энтропия обладает свойством аддитивности: Sсист.= S1+ S2+ S3+…+ Sn;
Тогда
S = f(W)+ f(W1)+ f(W2)+ f(W3)+…+ f(Wn) = f(W1*W2*W3*…*Wn)
Таким условиям отвечает только логарифмическая функция:
S = klnW+const…, где const — можно считать равной нулю (const=0), тогда получаем
уравнение Больцмана:
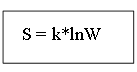 , где
, где 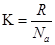 - постоянная Больцмана.[Дж/К]
- постоянная Больцмана.[Дж/К]
ТЕРМОДИНАМИЧЕСКИЙ ВЗГЛЯД НА ЭНТРОПИЮ
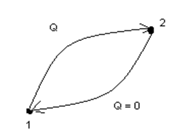
Рассмотрим круговой процесс, где теплота процесса 1-2: Q = ∆U+W1, а процесса 2-1: 0= - ∆U+W2, т.к. будем считать, что теплообмена здесь не происходит. Общее количество теплоты всего процесса 1-2-1: Q = W1+W2. С точки зрения второго закона термодинамики такие процессы, где все тепло переходит в работу, невозможны.
Принцип Каратеодори:
Вблизи каждого термодинамического состояния есть такое термодинамическое состояние, в которое невозможно прийти адиабатным путем, т.е. без теплообмена (Q =0).
Подводя к системе тепло, мы тем самым изменяем некоторую функцию состояния системы, которая зависит от количества теплоты — называемую энтропией (S).
Дата добавления: 2016-02-02; просмотров: 2827;
