Объединенное выражение Iи II— закона термодинамики

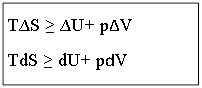
ЭНТРОПИЯ, КАК КРИТЕРИЙ НАПРАВЛЕННОСТИ

САМОПРОИЗВОЛЬНЫХ ПРОЦЕССОВ.

Рассмотрим изолированную систему.

В изолированной системе : Q= 0

Обратимый процесс: , .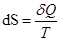

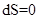Необратимый процесс: , .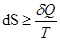

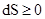В изолированной системе все самопроизвольные процессы идут в направлении увеличения энтропии системы, и пределом процесса является max. и постоянное значение энтропии.

В неизолированных системах энтропия может возрастать, убывать и быть постоянной, поэтому не является критерием направленности протекания самопроизвольных процессов.

ЭНЕРГИЯ ГИББСА И ЭНЕРГИЯ ГЕЛЬМГОЛЬЦА

TdS≥dU+pdV; dU- TdS+pdV=0.

1. Энергия Гельмгольца (Т=const, V=const)

При V=const: dU- TdS≤0

dU- TdS - SdT≤- SdT

dU- d(TS) ≤- SdT

При Т=const: dU- d(TS) ≤ 0;

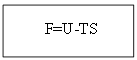
dF≤ 0.

При постоянном объеме и температуре все самопроизвольные процессы идут в сторону уменьшения энергии Гельмгольца до её постоянного min-ого значения.

2. Энергия Гиббса (Т=const, Р=const)

dU–TdS+pdV-SdT+Vdp≤ -SdT+Vdp;

(Т=const, V=const)

d(U–TS+pV)≤ -SdT+Vdp;

d(U–TS+pV)≤0

dG≤0

G=U-TS+pV;

При постоянном давлении и температуре все самопроизвольные процессы идут в сторону уменьшения энергии Гиббса до его постоянного min-ого значения.

Физический смысл:

1. ∆F

δW=TdS-dU —обратимый процесс.

δW= -dF

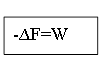
Убыл энергии Гельмгольца равна max работе процесса.

1) ∆G

W=W’+ p∆V

W’=W — p∆V

δW’= δW— p∆V

δW’= TdS – dU- pdV(обр)

δW’= -dG

Полезная работа:

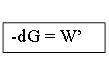
Убыл энергии Гиббса равна max полезной работе процесса.

ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ,

КАК КРИТЕРИЙ САМОПРОИЗВОЛЬНОГО ПРОЦЕССА

1. G = U–TS+pV;

2. F = U-TS;

3. H= U+pV;

4. dU≤ TdS-pdV.

1) dG = dU–TdS –SdT+pdV+Vdp;

dG ≤ TdS- pdV - TdS –SdT +pdV+Vdp;

dG = –SdT+Vdp;

T=const; P= const.

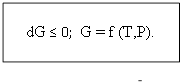
dG ≤ 0; G = f (T,P).

2) dF = dU–TdS –SdT;

dF ≤ TdS-pdV–TdS –SdT;

dF ≤ -pdV–SdT;

V=const; T= const.

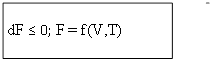
dF ≤ 0; F = f(V,T)

3) dH = dU+pdV+Vdp;

dH ≤ TdS-pdV +pdV+Vdp;

dH ≤ TdS+Vdp;

S=const; P= const

dH ≤ 0; H= f (S,P).

4) dU≤ TdS-pdV;

S=const; P= const

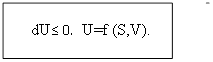
dU≤ 0. U=f (S,V).

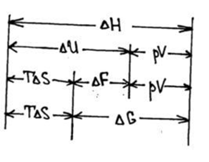
ТЕРМОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ

Это функции, с помощью которых или их частных производных можно выразить в явном виде параметры состояния.

1. G = f (T,P);

2. F = f(V,T);

3. H= f (S,P);

4. U=f (S, V).

1) ;

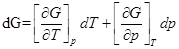dG = –SdT+Vdp;

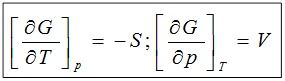
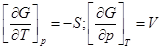
2) ;

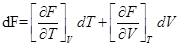dF = -pdV–SdT;

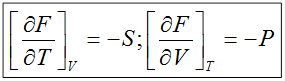
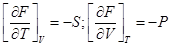
3) ;

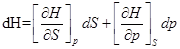dH = TdS+Vdp;

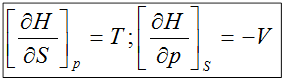
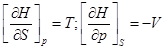
4) ;

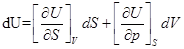dU≤ TdS-pdV;

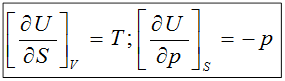
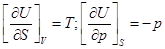
Функции энергии Гиббса, Гельмгольца, энтальпия и внутренней энерги являются характеристическими.

Поясним их смысл:

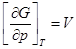
V= 0; p↑;G↑.

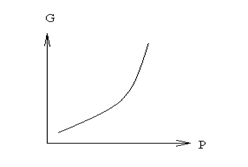
2.

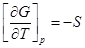
S˃0; -S˂0

T↑G↓

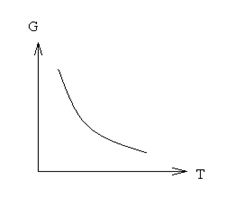
УРАВНЕНИЕ ГИББСА—ГЕЛЬМГОЛЬЦА

G=H-TS; F=U-TS.

Подставим вместо энтропии ее значение через частную производную энерги Гиббса и Гельмгольца:

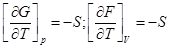
Тогда, уравнение Гиббса-Гельмгольца для системы:

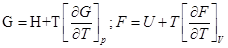
Уравнение Гиббса-Гельмгольца для процесса:

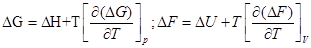
Эти уравнения показывают изменение энергии Гиббса и Гельмгольца при изменении температуры, также они связывают энергию Гельмгольца с тепловыми эффектами процесса(∆U и ∆F). При этом энтропия в явном виде не используется.

ХИМИЧЕСКИЙ ПОНЕНЦИАЛ

2CO+O₂=2CO₂

∑μ_idn_i=∑μ_idn;

dG = –SdT+Vdp, G = f (T,P)—уравнение справедливо, если система является закрытой и в ней не идет химическая реакция (состав системы не меняется).

Энергия множества переменных (компонентов), которые рассматриваются как независимые переменные: G =f (T,P,n₁,n₂,n₃…n_i).

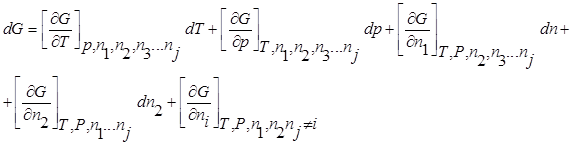
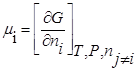
Химическим потенциалом данного компонента называется частная производная соответствующей термодинамической функции по числу молей данного компонента при условии постоянства параметров, функцией которых данная термодинамическая функция является.

Химический потенциал — это есть изменение энергии Гиббса (или любой другой термодинамической функции) при введении в большой энергии системы 1 моля данного вещества.

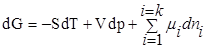,где к— число компонентов.

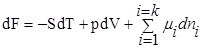
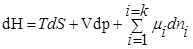
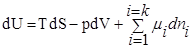
При T=const, P=const

,

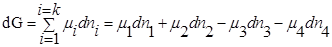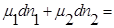
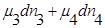
где 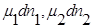— продукт, а 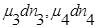— исходные вещества.

Для индивидуального вещества химический потенциал равен соотвественно термодинамической функции (в частности энергии Гиббса).

Химический потенциал компонента тождественен мольной энергии Гиббса. Для определения мольной энергии Гиббса i-ого компонента в условиях, отличных от стандартных, можно воспользоваться соотношением, которое справедливо для идеальных газов G _i не зависит от вида и концентрации других компонентов:

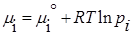- (для газов)

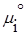— стандартный химический поненциал; P_i — парциальное давление данного компонента.

Т =298К, Р= 1атм, R=8,314 Дж/(моль*К),

Парциальное давление — это объем одного газа, который занимал бы вес объём данного газа. ∑p_i=p

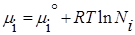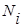, где — мольная доля компонентов в растворе.