Аналитическое выражение гомотетии
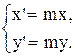
Свойство 3. Если прямая содержит центр гомотетии, то при этой гомотетии она преобразуется сама в себя, если прямая не содержит центра , то она переходит в прямую, ей параллельную.
Свойство 4. При гомотетии сохраняется простое отношение трех точек.
Свойство 5. При гомотетии отрезок преобразуется в отрезок, a луч - в луч.
При доказательстве этого свойства следует провести те же рассуждения, что и случаях доказательств свойств 4 и 5 движений (см. 33).
Свойство 6. При гомотетии угол преобразуется в равный ему угол.
Теорема 1. Любое подобие p можно представить как произведение d · H, где d - движение плоскости, a H - некоторая гомотетия.
Доказательство. Пусть k - коэффициент подобия p. Рассмотрим гомотетию 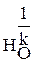 с произвольным центром О и коэффициентом
с произвольным центром О и коэффициентом  . Легко видеть, что произведение d = p ·
. Легко видеть, что произведение d = p · 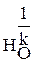 является движением. Действительно, если A и В - две произвольны точки, то:
является движением. Действительно, если A и В - две произвольны точки, то:
½ 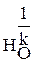 (A)
(A) 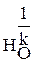 (B) ½ =
(B) ½ = 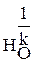
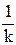 ½AB½
½AB½
и
½p · 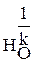 (A) p ·
(A) p · 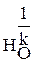 (B) ½ = ½
(B) ½ = ½ 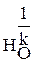 (A)
(A) 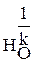 (B) ½.
(B) ½.
Отсюда следует, что ½d(A) d(B)½ = ½AB½. Преобразование в сохраняет расстояния между точками. При доказательстве свойства 2, § 39 мы получили, что 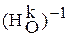 =
= 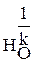 , поэтому d ·
, поэтому d · 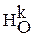 = (p ·
= (p · 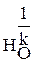 ) ·
) · 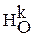 = p. Теорема доказана.
= p. Теорема доказана.
Замечание 1. Из доказанной теоремы следует, что в качестве центра гомотетии О можно взять любую точку плоскости, а её коэффициент равен коэффициенту подобия.
Замечание 2. Легко показать, что произведение H·d также является подобием.
Свойство 1. При подобии прямая преобразуется в прямую, луч - в луч, отрезок - в отрезок, a угол - в равный ему угол.
Определим аналитические выражения подобия. Представим данное подобие p в виде произведения d · H движения d на гомотетию H, причем в качестве центра гомотетии примем начало прямоугольной декартовой системы координат. Тогда аналитические выражения движения и гомотетии имеют вид (35.6) и (39.5):
d:  H:
H: 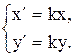
Для нахождения формул произведения d · H следует подставить аналитические выражения (39.5) гомотетии H в формулы (39.5) анaлитических выражений движения d. Получим
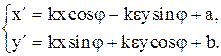 (40.1)
(40.1)
Если k = 1, то подобие является движением. При этом соотношения (9.1) совпадают с формулами (35.6).
Теорема 2. Любое подобие, отличное от движения, имеет одну и только одну инвариантную точку.
Доказательство. Пусть p подобие плоскости, отличное от движения. Тогда его коэффициент k не совпадает с единицей. Аналитические выражения подобия имеет вид (40.1). Точка M тогда и только тогда является инвариантной точкой подобия p, когда её координаты x и у удовлетворяют системе уравнений:
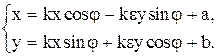
Преобразуем её к виду:
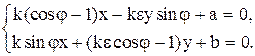 (40.2)
(40.2)
Система линейных уравнения тогда и только тогда имеет единственное решение, когда она имеет определитель, отличный от нуля. В случае подобия первого рода e = 1, определитель D системы (40.2) имеет вид:
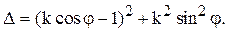
Поэтому D = 0 в том и только в том случае, когда

Из второго равенства следует, что j = kp. Тогда из первого получим: k = 1 или k = -1. Так как коэффициент подобия всегда положителен, то k ¹ -1. Кроме того, данное подобие отлично от движения, поэтому k ¹ 1. Таким образом, D ¹ 0. Для подобий первого рода утверждение доказано.
Рассмотрим теперь подобие второго рода. В этом случае e = -1. Определитель системы (40.2) имеет вид:

По условию подобие не является движением, поэтому k ¹ 1. Отсюда следует, что D ¹ 0, и система (40.2) имеет единственное решение. Теорема доказана полностью.
Следствие. Если подобие имеет две неподвижные точки или не имеет их вообще, то оно является движением.
Определение 1. Инвариантная точка подобия, отличного от движения, называется его центром.
Проведем классификацию подобий. Пусть p подобие первого рода, отличное от движения. Согласно доказанной теореме, оно имеет единственную неподвижную точку O. Представим его в виде произведения гомотетии H на движение d: p = d · H. В соответствии со следствием теоремы 1, можно считать, что центр О подобия совпадет с центром гомотетии. Легко видеть, что в этом случае О - также единственная неподвижная точка движения d. Так как p - подобие первого рода, то d - также движение первого рода. Поэтому из теоремы Шаля следует, что оно является либо параллельным переносом, либо вращением (cм. § 36, теорему 1). Но параллельный перенос не имеет неподвижных точек, поэтому d представляет собой вращение плоскости вокруг центра подобия, точки O. Таким образом, подобие первого рода, отличное от движения, является произведением гомотетии на вращение, причем центр подобия представляет собой и центр гомотетии, и центр вращения. Такого рода подобие называется центрально-подобным вращением.
Пусть p- подобие второго рода, отличное от движения. Обозначим через О его центр подобия и представим p в виде произведения d · H гомотетии на движение. без ограничения общности можно считать, что О - центр гомтетии H. Кроме того, О - единственная неподвижная точка движения d. Из теоремы 3, § 36 видно, что d совпадает либо с осевой, либо co скользящей симметрией. Но скользящая симметрия не имеет инвариантных точек. Поэтому в данном случае движения d - осевая симметрия, причем центр гомотетии О принадлежит её оси. Таким образом, рассматриваемое подобие представляет собой произведение гомотетии на осевую симметрию, а её центр совпадает с центром гомотетии и лежит на оси симметрии. Такого рода подобия называются центрально-подобными симметриями.
Мы провели классификацию подобий первого и второго рода, отличных от движений. Движения, в свою очередь, являются частными случаями подобий. Их классификацию была приведена в указанных теоремах параграфа 36. Итак, доказано следующее утверждение.
Теорема 3. Любое подобие первого рода является либо параллельным переносом, либо вращением, либо центрально-подобным вращением, а подобие второго рода - либо скользящей, либо осевой, либо центрально-подобной симметрией.
Теорема 4. Подобия плоскости образуют группу преобразований.
Доказательство. Нам достаточно проверить, что как произведение подобий, так и обратное к подобию преобразование также являются подобиями.
Пусть даны подобия p  и p
и p  , коэффициенты которых равны k
, коэффициенты которых равны k  и k
и k  . Рассмотрим две произвольные точки A и B. Пусть A'= p
. Рассмотрим две произвольные точки A и B. Пусть A'= p  (A), A"= = p
(A), A"= = p  · p
· p  (A), B'= p
(A), B'= p  (B), B"= p
(B), B"= p  · p
· p  (B). Так как p
(B). Так как p  и p
и p  - подобия, то
- подобия, то
½A"B"½ = ½ p  (A') p
(A') p  (B')½ = k
(B')½ = k  ½A'B'½ = k
½A'B'½ = k  ½ p
½ p  (A) p
(A) p  (B)½= k
(B)½= k  k
k  ½AB½.
½AB½.
Таким образом, произведение p  · p
· p  - подобие с коэффициентом k
- подобие с коэффициентом k  k
k  .
.
Рассмотрим некоторое подобие p с коэффициентом k и обозначим через A  и В
и В  прообразы двух произвольных точек A и B: A
прообразы двух произвольных точек A и B: A  = p
= p 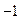 (A), B
(A), B  = p
= p 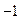 (B). Тогда p(A
(B). Тогда p(A  ) = A, p(В
) = A, p(В  ) = B. Так как p - подобие, то ½AB½ = k½A
) = B. Так как p - подобие, то ½AB½ = k½A  B
B  ½, следовательно, ½A
½, следовательно, ½A  B
B  ½=
½=  ½AB½. Отсюда вытекает, что обратное преобразование p
½AB½. Отсюда вытекает, что обратное преобразование p 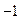 также является подобием с коэффициентом
также является подобием с коэффициентом  . Теорема доказана.
. Теорема доказана.
Две фигуры F и F' называются подобными, если существует такое преобразование подобия p, при котором F' = p (F).
В школьном курсе геометрии фундаментальное значение имеют свойства подобных треугольников. Докажем теорему.
Теорема 5. Два треугольника АВС и А¢В¢С¢ подобны между собой в том и только в том случае, когда
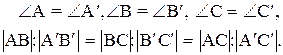 (41.1)
(41.1)
Доказательство. Пусть существует преобразование подобия p, при котором p(A) = A', p(B) = B', p(C) = C'. Из свойств подобий следует, что углы преобразуются в равные углы , a отношение соответствующих отрезков равно коэффициенту подобия. Поэтому для подобных треугольников справедливы соотношения (41.1). 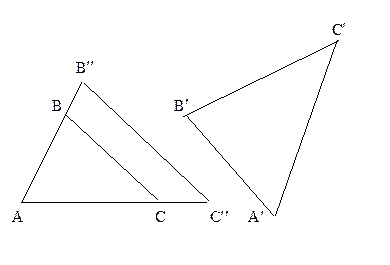
Обратно. Пусть даны треугольники АВС и А’В’С’, для которых выполнены равенства (41.1). Рассмотрим гомотетию 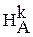 с центром в точке A и коэффициентом k = ½AB½:½A'B'½. Обозначим через D" и C" образы вершин В и С при этой гомотетии: D"=
с центром в точке A и коэффициентом k = ½AB½:½A'B'½. Обозначим через D" и C" образы вершин В и С при этой гомотетии: D"= 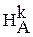 (В), C"=
(В), C"= 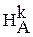 (С). Тогда ½AB"½:½AB½ = ½AC"½:½AC½ = ½B"C"½:½BC½ = k. Из равенств (41.7) следует, что ½AB"½= ½A'B'½, ½AC"½ = ½A'C'½, ½B"C"½= ½B'C'½. При гомотетии сохраняются углы треугольника. Поэтому Ð B"= Ð B', Ð C"= Ð C'. Соответственные стороны и углы треугольников А’В’С’ и А””є равны между собой (рис. 169). Согласно теореме 3, § 34 эти треугольники равны между собой. Отсюда следует, что существует движение d, переводящее один треугольник во второй: d(A”)=A', d(B")=B', d(C")=C'. Следовательно, подобие p = d·
(С). Тогда ½AB"½:½AB½ = ½AC"½:½AC½ = ½B"C"½:½BC½ = k. Из равенств (41.7) следует, что ½AB"½= ½A'B'½, ½AC"½ = ½A'C'½, ½B"C"½= ½B'C'½. При гомотетии сохраняются углы треугольника. Поэтому Ð B"= Ð B', Ð C"= Ð C'. Соответственные стороны и углы треугольников А’В’С’ и А””є равны между собой (рис. 169). Согласно теореме 3, § 34 эти треугольники равны между собой. Отсюда следует, что существует движение d, переводящее один треугольник во второй: d(A”)=A', d(B")=B', d(C")=C'. Следовательно, подобие p = d· 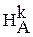 переводит треугольник АВС в треугольник А’В’С’. Теорема доказана.
переводит треугольник АВС в треугольник А’В’С’. Теорема доказана.
В школьных учебниках по определению под подобными понимаются такие треугольники, которые удовлетворяют условиям (41.1). Под подобными же многоугольниками понимаются такие, у которых соответственные стороны пропорциональны, а соответственные углы равны между собой. Можно доказать, что и в этом случае существует подобие, переводящее один многоугольник во второй. В заключение докажем следующую теорему.
Теорема 6. Любые две параболы подобны между собой.
Доказательство. Рассмотрим две параболы g  и g
и g  . Как известно из первой части курса геометрии, существуют ортонормированные реперы
. Как известно из первой части курса геометрии, существуют ортонормированные реперы 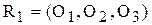 и
и 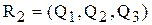 , в которых их уравнения имеют канонический вид: g
, в которых их уравнения имеют канонический вид: g  : y =2 p
: y =2 p  x , g
x , g  : y =2 p
: y =2 p  x. Как следует из теоремы 1, § 34, существует движение d, которое переводит репер R
x. Как следует из теоремы 1, § 34, существует движение d, которое переводит репер R  в R
в R  . При этом парабола g
. При этом парабола g  преобразуется в параболу g‘, которая в репере R
преобразуется в параболу g‘, которая в репере R  имеет то же уравнение y = 2p
имеет то же уравнение y = 2p  x, что и парабола g
x, что и парабола g  в репере R
в репере R  (рис. 170).
(рис. 170).
Рассмотрим гомотетию 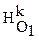 с центром в точке О
с центром в точке О  и коэффициентом k = p
и коэффициентом k = p  : p
: p  . Пусть g"=
. Пусть g"= 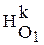 (g'). Легко видеть, что уравнение g" в репере R
(g'). Легко видеть, что уравнение g" в репере R  имеет вид y =2 p
имеет вид y =2 p  x. Поэтому параболы g" и g
x. Поэтому параболы g" и g  совпадают друг с другом. Таким образом, подобие p =
совпадают друг с другом. Таким образом, подобие p =  · d переводит g
· d переводит g  в g
в g  . Теорема доказана.
. Теорема доказана.
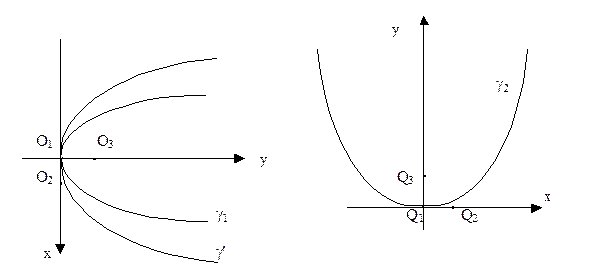 |
Можно показать, что два эллипса (гиперболы) подобны друг другу в том и только в том случае, когда совпадают их эксцентриситеты.
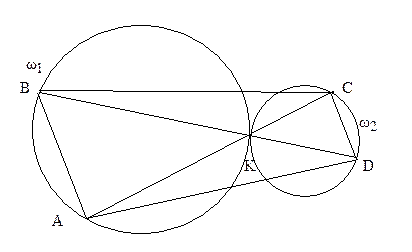
Пример 1. Даны две окружности 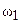 и
и 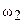 , которые касаются в точке К. Через точку К проведены две секущие, первая пересекает
, которые касаются в точке К. Через точку К проведены две секущие, первая пересекает 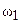 и
и 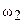 , в точках А и С, а вторая в точках B и D. Доказать, что четырехугольник АВСD – трапеция.
, в точках А и С, а вторая в точках B и D. Доказать, что четырехугольник АВСD – трапеция.
 |
Дата добавления: 2016-02-02; просмотров: 2130;
