Аналитическое описание процесса.
Аналитическое описание процесса нестационарной теплопроводности включает в себя дифференциальное уравнение и условия однозначности.
Дифференциальное уравнение теплопроводности при qv = 0 имеет вид:
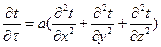 (78)
(78)
Условия однозначности задаются в виде:
1) Физических параметров a, λ,c, ρ.
2) Формы и геометрических размеров тела l0, l1, … ,ln
3) Температуры тела в начальный момент времени (79)
τ = 0 : t= t0= f(x,y,z)
4) Граничные условия задаются чаще всего в виде
граничных условий Ш рода: 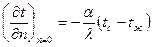
Дифференциальное уравнение теплопроводности (78) совместно с условиями однозначности (79) дает законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции:
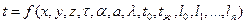 , (80)
, (80)
которая удовлетворяла бы уравнению (78) и условиям (79).
Рассмотрим более подробно решение данной задачи, т.е. нахождение функции вида (80) для различных тел.
3. Охлаждение (нагревание) неограниченной пластины.
Задача формулируется следующим образом. Плоская неограниченная пластина (стенка) толщиной 2δ, имеющая начальный момент времени τ=0 во всех точках одинаковую температуру t0, помещается в среду, температура которой tж < t0.
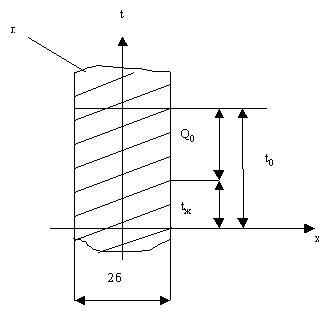
Рис.10. К охлаждению плоской
неограниченной пластины (при
τ=0, задано t0=const, θ0=const)
Граничные условия III рода.
Температура среды tж во время охлаждения поддерживается постоянной. Охлаждение пластины происходит через обе ее поверхности с одинаковой интенсивностыо путем теплоотдачи. Коэффициент теплоотдачи α задан и остается постоянным в течение всего процесса. Известен также материал, из которого выполнена пластина, т.е. известны его теплофизические характеристики
a, λ, c, ρ. Требуется найти температурное поле пластинки в произвольный момент времени t >0.
Отсчет температуры пластины для любого момента времени будем вести от температуры окружающей среды tж, т.е.
t - tж = θ
Будем называть θ избыточной температурой. С учетом этого обозначения и с учетом того, что температурное поле при заданных условиях будет одномерным, математически задачу можно сформулировать следующим образом.
Дифференциальное уравнение теплопроводности:
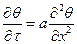 (81)
(81)
Начальные условия: при τ=0: θ= θ0= t0 – tж (82)
Граничные условия: на оси пластины при x=0: 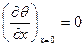
на поверхности пластины при х= 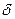 :
: 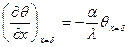
Решение уравнения (81) проводят одним из методов, разработанных математической физикой, чаще всего методом разделения переменных, который заключается в следующем.
Решение дифференциального уравнения (81) ищем в виде произведения двух функций, одна из которых является функцией только времени τ, а другая - только координаты х.
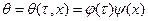 (83)
(83)
После подстановки (83) в уравнение (81) получим:
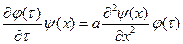
или 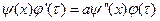
Разделив переменные в последнем уравнении, запишем:
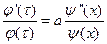 (84)
(84)
Левая часть уравнения (84) есть функция только τ, a правая - функция только х.
Если зафиксировать аргумент х и менять только τ, то при любом его значении левая часть уравнения (84) равна постоянной величине, стоящей в правой части, т.е. φ′(τ)/φ(τ)=const.Аналогично при фиксации τ и изменении х правая часть уравнения (84) для любого значения х должна равняться постоянной величине, стоящей в левой части, которая зависит только от τ, т.е. ψ″(x)/ψ(x)=const.
Так как равенство (84) должно иметь место при любых значениях x и τ, то обе его части должны быть равны одной и той же постоянной величине. Обозначим эту величину –k2=const. Постоянным k определяется из граничных условий, а знак минус перед k2 объясняется следующим. Искомое решение должно удовлетворять исходному дифференциальному уравнению (81) для затухающего процесса (в данном случае уравнению теплопроводности), при котором тело стремится к равновесному тепловому состоянию, а это может быть обеспечено лишь при отрицательном k2.
Исходя из сказанного уравнение (84) запишем в виде:
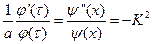
откуда 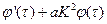 =0 (85)
=0 (85)
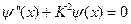 (86)
(86)
В результате мы получили систему обыкновенных дифференциальных уравнений (85) и (86).
Уравнению (85) удовлетворяет функция:
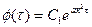 , (87)
, (87)
где экспоненциальная функция ℮-ak 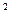 τ с увеличением времени стремится к нулю, т.е. обеспечивает затухание процесса;
τ с увеличением времени стремится к нулю, т.е. обеспечивает затухание процесса;
Уравнению (86) удовлетворяет функция:
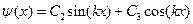
Подставляя полученные выражения для φ(τ) и ψ(x) в уравнение (83),  получаем частное решение:
получаем частное решение:
 (88)
(88)
Выражение (88) удовлетворяет исходному уравнению (84) при любых значениях постоянных С1, С2, С3 и k.
Чтобы уравнение (88) было решением поставленной задачи, его нужно подчинить начальным и граничным условиям.
Подчиняя уравнение (88) граничным условиям (82) при х=0:


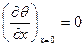 ,
,
находим: 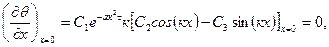
или 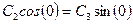 , т.е.
, т.е. 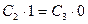
Следовательно, С2=0.
Это означает, что частное решение
ψ(x)= С2*sin(kx)
использовать нельзя, т.к. оно не удовлетворяет заданным граничным условиям. Действительно, поскольку sin(kx) является нечетной функцией, т.е. такой, которая меняет свой знак при переходе от +х к -х, а не нашей задаче температура (функция) остается положительной независимо от х.
Если учесть, что С2=0 и обозначить С1*С2=А, то уравнение (88) принимает вид:
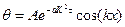 (89)
(89)
Подчиняя (89) второму граничному условию
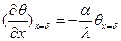 , (90)
, (90)
получим:
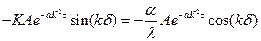 (91)
(91)
Из уравнения (91) получаем
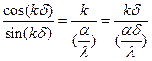 ,
,
или 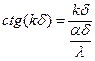 (92)
(92)
В уравнении (92) обозначим:
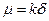 ,
, 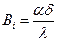 ,
,
где 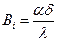 - безразмерный комплекс, называемый числом Био.
- безразмерный комплекс, называемый числом Био.
Число Bi является важной характеристикой процесса теплопроводности. Оно представляет собой отношение внутреннего термического сопротивления теплопроводности δ/λ к внешнему термическому сопротивлению теплоотдачи 1/α:
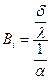
Тогда уравнение (92) запишется
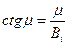 (93)
(93)
Уравнение (93) называют характеристическим уравнением. Анализ этого уравнения показывает, что при каждом значении числа Bi существует бесконечное множество решений. Наиболее просто уравнение (93) решается графическим способом. Обозначим левую часть (93) через y1=ctgμ, а правую- через y2=μ/Bi. п 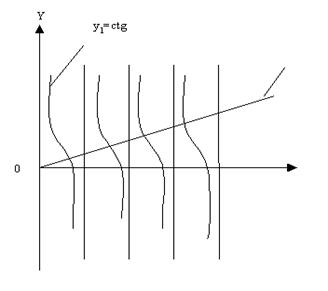 ересечение котангенсоиды y1 с прямой y2 дает значение корней характеристического уравнения, т.е. μ (рис. 11). Из рис. 11 следует, что мы имеем бесконечное множество значений величины μn, причем каждое последующее больше предыдущего:
ересечение котангенсоиды y1 с прямой y2 дает значение корней характеристического уравнения, т.е. μ (рис. 11). Из рис. 11 следует, что мы имеем бесконечное множество значений величины μn, причем каждое последующее больше предыдущего:
μ1 < μ2 < μ3 <…<μn<…
Важно отметить, что каждому значению числа Bi отвечает своя
Рис.11. Решение уравнения (93). совокупность корней уравнения (93).
При Bi→∞ прямая y2=μ/Bi совпадает с осью абсцисс и корни уравнения (93) будут равны:
μ1=π/2, μ2=3π/2, μ3=5π/2, … , μn=(2n-1)π/2
При Bi→0 прямая y2=μ/Bi совпадает с осью
ординат, при этом корни уравнения (93)
равны:
μ1=0, μ2=π, μ3=2π, … , μn=(n-1)π,
где n = 1, 2, 3 …
Для других конечных значений числа Bi величины μn имеют промежуточные значения и приводятся в таблицах справочной и учебной литературы.
Уравнение (89) представим в следующем виде:
 ,
,
где
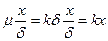 ,
,
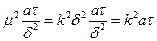
каждому найденному значению корня будет соответствовать свое частное распределение температуры:
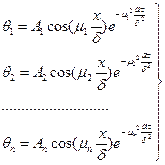 (94)
(94)
Полученные частные решения (94) будут удовлетворять дифференциальному уравнению (2.96) при любых значениях постоянных А1, А2, … , Аn, но ни одно из этих решений не будет соответствовать действительному распределению температуры в теле. Однако путем наложения бесконечного числа таких распределений при соответствующем выборе значений Аn можно воспроизвести любую действительную температурную кривую.
На основании сказанного общее решение можно представить суммой бесконечного ряда:
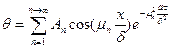 (95)
(95)
Постоянную Аn в уравнении (94) находят, подчиняя уравнение (94) начальному условию.
Опуская промежуточные выводы, приведем результирующее выражение для коэффициента Аn в данной задаче:
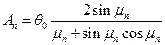 (96)
(96)
Подставляя значение Аn, записанное для случая равномерного распределения температуры в пластине в начальный момент времени, в уравнении (94), окончательно получим:
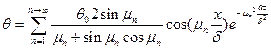 (97)
(97)
Уравнению температурного поля (96) обычно придают безразмерную форму. Разделим левую и правую части уравнения (96) на θ0.
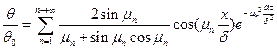 (98)
(98)
В уравнении (98) введем следующие обозначения:
Θ=θ/θ0 - безразмерная температура;
Χ=х/δ - безразмерная координата;(отметим, что X меняется от 0 до 1).
F0=aτ/δ2 - число Фурье, представляющее собой безразмерный комплекс (часто называют - безразмерное время);
Dn= Аn/θ0=2sin μn /(μn+ sin μn *cos μn) - безразмерный коэффициент.
С учетом этих обозначений уравнение (97) принимает вид:
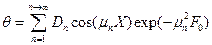 (99)
(99)
Значения Dn=f(Bi) и μn= f(Bi) приводятся в справочной литературе.
3.1.Анализ полученного решения.
Так как μ1, μ2, μ3,…, μn представляет собой ряд возрастающих чисел, то чем больше μ, тем меньше роль последующего члена ряда по сравнению с предыдущим. Кроме того, чем больше число F0 , тем быстрее будут убывать члены ряда с увеличением n.
Многочисленные исследования показали, что уже при F0≥0,3 ряд (99) становится настолько быстросходящимся, что распределение температуры достаточно точно можно описать первым членом ряда:
 (100)
(100)
или 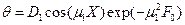 (101)
(101)
Величина D1 является функцией только числа Bi и, как сказано выше, приводится в таблицах. Кроме того, если рассматривать температуру для определенного значения X , то и cos(μ1*X ) становится функцией только числа Bi.
Для оси пластины Χ=х/δ=0 и сos(μ1*0)=1,
Для поверхности пластины Χ=х/δ=1 и сos(μ1*1)= сosμ1
Для оси пластины произведение D1cos(0)=D1 обозначим как функцию N(Bi). Тогда уравнение (101) принимает вид:
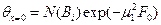 (102)
(102)
Для поверхности пластины произведение D1cosμ1 обозначим как функцию P(Bi) и уравнение (102) запишется:
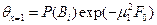 (103)
(103)
Функции N(Bi) и P(Bi) табулированы и для расчета могут быть взяты из справочников.
Из уравнения (99) следует, что при охлаждении (нагревании) пластины для любого момента времени при заданных граничных условиях поле температуры будет иметь вид симметричной кривой с максимумом на оси пластины (X=0). Для каждого последующего момента будет своя кривая, монотонно убывающая к поверхностям пластины. При этом для любого момента времени касательные к температурным кривым в точках X= ±1 проходят через две направляющие точки +А и –А, расположенные на расстоянии ±Х0 от поверхности пластины, причем Х0 =1/Bi (рис.12).
Для доказательства этого свойства рассмотрим температурное поле для произвольного момента времени F0>0.
Умножив граничное условие (2.98) при x=δ на δ/θ0, получим:

Запишем последнее выражение в безразмерной форме:
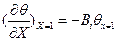 (а)
(а)
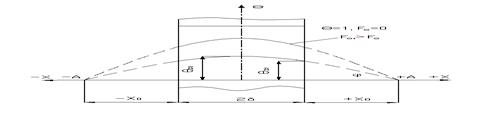 |
Рис.12. Изменение температурного поля в неограниченной пластине при ее охлаждении.
Из рис.12 следует, что
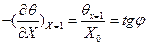 (б)
(б)
Из выражения (а) и (б) получаем
Х0 = 1/Bi (104)
Из уравнения (104) следует, что расстояние точки А от поверхности пластины определяется заданными условиями однозначности, которые справедливы для любого момента времени. Сказанное справедливо не только для пластины, но и для цилиндра, шара и тел других геометрических форм.
Доказанное свойство температурных кривых дает возможность определить характер изменения температуры в теле при заданном значении числа Bi. Рассмотрим при этом три случая.
Рис.13.Распределение температуры при охлаждении пдастины.
 1. Bi→∞ (практически Bi >100).
1. Bi→∞ (практически Bi >100).
Если число Bi стремится к бесконечности, то температура поверхности пластины сразу становится равной температуре окружающей среды tж, в которую помещена пластина.
Рис.14.Распределение
температуры при
охлаждении пластины.
Последнее следует из уравнения (104): при Bi→∞ Х0=1/Bi=0. Это означает, что точка пересечения касательных к температурным кривым с осью X находится на поверхности пластины (рис.13). Из выражения для числа 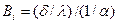 следует, что при заданных конечных значениях δ и λ, Bi→∞ тогда, когда α→∞, т.е. когда имеет место очень большая интенсивность отвода теплоты от поверхности. В этих случаях процесс охлаждения определяется физическими свойствами и размерами тела.
следует, что при заданных конечных значениях δ и λ, Bi→∞ тогда, когда α→∞, т.е. когда имеет место очень большая интенсивность отвода теплоты от поверхности. В этих случаях процесс охлаждения определяется физическими свойствами и размерами тела.
2. Очень малые числа Bi (практически Bi <0,1).
При малых числах Bi температура на поверхности пластины незначительно отличается от температуры на оси, т.е. температура по толщине пластины распределяется равномерно и кривая температур остается почти параллельной оси ОХ для любого момента времени (рис.14).
При Bi→0 Х0=1/Bi→∞. Т.е. касательные к температурным кривым в точках пересечения их с поверхностью должны пересекаться с осью абсцисс в бесконечности.
 Из выражения
Из выражения 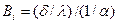 видно, что малые значения числа Bi могут иметь место при малых размерах толщины пластины δ, при больших значениях коэффициента теплопроводности λ и малых значениях коэффициента теплоотдачи α.
видно, что малые значения числа Bi могут иметь место при малых размерах толщины пластины δ, при больших значениях коэффициента теплопроводности λ и малых значениях коэффициента теплоотдачи α.
В рассматриваемом случае процесс охлаждения (нагрева) тела определяется интенсивностью теплоотдачи на поверхности пластины.
Иначе говоря, процесс выравнивания температуры в теле происходит существенно интенсивнее, чем отвод теплоты с поверхности. Задача становится внешней.
Рис.15. Распределение
температуры при
охлаждении пластины
/3. Число Bi находится в пределах 0,1≤ Bi < 100.
 В этом случае температурные кривие для любого момента времени будут выглядеть так, как показано на рис. 15.
В этом случае температурные кривие для любого момента времени будут выглядеть так, как показано на рис. 15.
Здесь интенсивность процесса охлаждения (нагревания) определяется как внутренним, так и внешним термическим сопротивлением.
3.2 Графическое решение задач нестационарной теплопроводности.
Как следует из уравнений (102) и (103), при заданной безразмерной координате X, безразмерная температура θ становится функцией только чисел Bi и F0:
 и
и 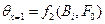
Логарифмируя уравнения (102) и (103), получим:
 (105)
(105)
Из уравнений (105) следует, что при заданном значении X и заданном Bi натуральный логарифм θ линейно зависит от времени (числа Фурье). Последнее обстоятельство дает возможность графического решения уравнений (102) и (103). В справочной и учебной литературе приводятся графики зависимости θ от чисел Bi и F0 для середины и поверхности пластины, которые имеют вид, представленный на рис. 16
 |
Рис.16. Зависимость θ=f1(Bi, F0) для середины пластины.
Порядок расчета температуры для середины пластины или для поверхности пластины (т.е. при X=0 илиХ=1) в заданный момент времени по графикам сводится к следующему:
1. Определяют число F0 по заданным τ, а и δ;
2. Вычисляют число Bi по известным α, λ и δ;
3. На оси абсцисс графика откладывают найденное значение числа F0, проводят вертикаль по наклонной прямой, соответствующей найденному значению Bi и, проектируя полученную точку на ось ординат, получают значение θ (рис.16).
4. По найденной безразмерной температуре θх=0 для середины пластины или θх=1 для поверхности пластины определяют исходную искомую температуру в середине пластины tх=0 или на поверхности пластины tх=δ.
С помощью указанных графиков можно решить обратную задачу: найти промежуток времени, необходимый для охлаждения (или нагревания) данной точки пластины (при X=0 или Х=1) до заданной температуры. В этом случае рассчитывают θ и Bi и по ним находят число F0 (см.рис.16). По найденному числу F0 вычисляют время τ.
Дата добавления: 2016-01-18; просмотров: 1854;
