А) Однослойная цилиндрическая стенка
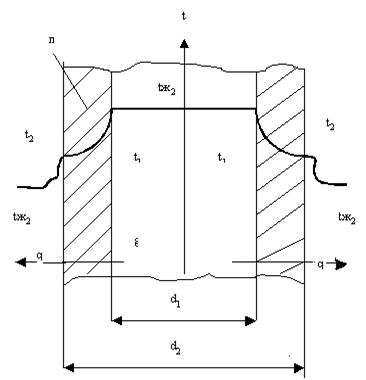
Рис.8. Однослойная цилиндрическая стенка. Г.У. III рода.
Рассмотрим однослойную (однородную) цилиндрическую стенку (трубу) с постоянным коэффициентом теплопроводности. Заданы постоянные температуры подвижных сред tж1 и tж2, и постоянные значения коэффициентов теплоотдачи на внутренней и наружной поверхностях стенки α1 и α2. Необходимо найти ql и температуры t1 и t2. Будем полагать, что длина трубы велика по сравнению с диаметрами. Тогда потерями теплоты с торцев трубы можно пренебречь и при установившемся тепловом режиме, количество теплоты, которое будет передаваться от горячей среды к внутренней поверхности стенки, проходить через стенку и отдаваться от наружной поверхности к холодной жидкости будет одно и то же.
Помня, что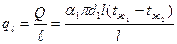 
можно написать:
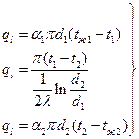(60)
Решаем эти уравнения относительно частных температурных напоров:
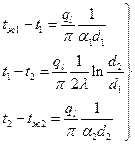(61)
Складывая уравнения (61), получаем:
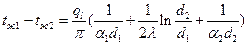
Отсюда:
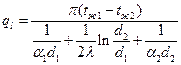(62)
Обозначим
, 
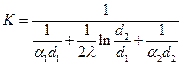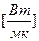(63)
Величина Kl называется линейным коэффициентом теплопередачи и имеет размерность, Вт/мК. Она характеризует интенсивность передачи тепла от одной среды к другой через разделяющую их стенку.
Линейный коэффициент теплопередачи численно равен количеству теплоты, которое проходит через стенку трубы длиной I м в единицу времени в радиальном направлении от одной среды к другой при разности температур между ними в один градус.
С учетом (63) уравнение (62) запишется в виде
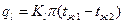(64)
Величина Rl=1/kl, мК/Вт, обратная kl, называется линейным термическим сопротивлением теплопередачи:
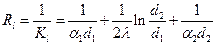(65)
где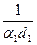 
- линейное термическое сопротивление теплоотдачи от греющей среды к стенке;
где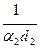 
- линейное термическое сопротивление теплоотдачи от стенки к нагреваемой среде;
1/2λ*ln(d2/d1) - линейное термическое сопротивление теплопроводности стенки.
При расчете теплопередачи через многослойную цилиндрическую стенку нужно учитывать линейное термическое сопротивление теплопроводности всех слоев. Тогда линейное техническое сопротивление теплопередачи для стенки из n слоев будет равно:
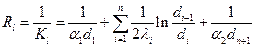(66)
Отсюда kl для многослойной стенки:
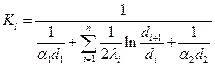(67)
Линейная плотность теплового потока:
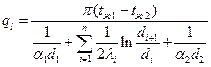(68)
Температура на поверхностях однослойной стенки найдем из уравнений (61):
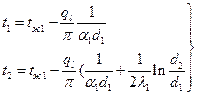(69)
Температуру t1 можно найти также через температуру второй жидкости tж2:
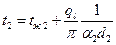(70)
В случае многослойной стенки получим:
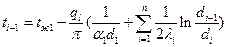(71)
А температуру на внешней поверхности многослойной стенки в это случае можно найти также через tж2:
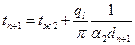(72)
В технических расчетах, когда толщина стенки трубы мала по сравнению с диаметрами, можно теплопередачу через цилиндрическую стенку считать как через плоскую. Покажем, что это действительно так.
Если тепловой поток через цилиндрическую стенку
отнести к внутренней или наружной поверхности стенки, то получим плотность теплового потока, Вт/м2, отнесенную к единице соответствующей поверхности трубы:
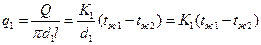
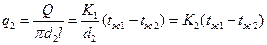
Формулы для К1 и К2, Вт/м2К, в развернутом виде:
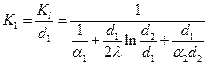(73)
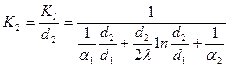(74)
Величину ln(d2/d1)разложим в ряд:
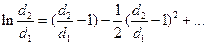
Вели отношение d2/d1→1, то такой ряд быстро сходится, и c достаточной точностью можно ограничиться первым членом ряда:
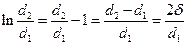(75)
где δ - толщина стенки трубы, (м).
Подставив (75) и условие d2/d1≈ d1/d2 ≈ 1 уравнения (73) и (74), получим:
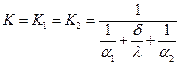(76)
Т.е. получили выражение коэффициента теплопередачи для плоской стенки (см. уравнение 38).
Следовательно, если стенка трубы тонкая, то при практических расчетах можно тепловой поток находить по формуле
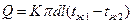, (77)
где К, находится по формуле (76)
Обычно в инженерных расчетах при d2/d1≤1,8 пользуются формулой (77).
Для уменьшения погрешности в качестве расчетной поверхности в (77), берут поверхность, со стороны которой α меньше:
если α1>>α2, то d=d2;
если α2<< α1, то d=d1.
если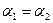 
, то d=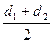 
Дата добавления: 2016-01-18; просмотров: 1192;