А) Однослойная стенка. Рис. 3. Однослойная плоская стенка
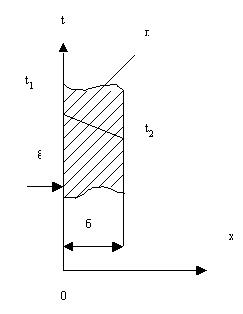
Рис. 3. Однослойная плоская стенка. Г.У. I рода.
Дана однородная и изотропная стенка (рис.3) толщиной δ с постоянным коэффициентом теплопроводности λ, два других размера стенки неограниченны. На наружных поверхностях стенки поддерживают постоянные температуры t1 и t2. При заданных условиях температура будет изменяться только в направлении оси Ox, т.е. температурное поле будет одномерным и
∂t/∂y = ∂t/∂z = 0
Тогда уравнение (24) принимает вид:
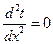 (25)
(25)
В уравнении (25) частная производная заменена полной, т.к. изменение температуры определяется только одной переменной X. Граничные условия в рассматриваемой задаче запишутся следующим образом:
при 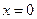
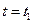
при 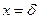
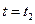 (26)
(26)
Уравнение (25) и условия (26) дают полную математическую формулировку рассматриваемой задачи.
В результате поставленной задачи должно быть найдено распределение температуры в плоской стенке, т.е. t = ƒ(x), и получена формула для определения плотности теплового потока.
Проинтегрируем дважды уравнение (25).
Первое интегрирование дает:
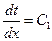 (27)
(27)
После второго интегрирования получим:
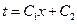 (28)
(28)
Постоянные интегрирования в (28) определяются из граничных условий (26):
при 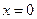
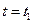 и
и 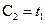
при 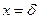
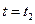 и
и 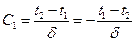
Подставляя значения С1 и С2 в уравнение (28), получим закон распределения температуры в рассматриваемой плоской стенке или, иначе, выражение для температурного поля:
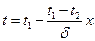 (29)
(29)
Для определения плотности теплового потока воспользуемся законом Фурье
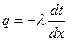
Учитывая, что
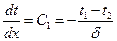
после подстановки dt/dx в выражение закона Фурье, получаем:
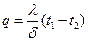 (30)
(30)
В уравнении (30):
t1 - t2 = Δt - температурный напор;
отношение λ/δ, Вт/м2К- тепловая проводимость стенки;
обратная величина Rc = δ/λ, м2К/ Вт - термическое сопротивление теплопроводности стенки.
Найдя плотность теплового потока, можно вычислить все тепло, которое передается через поверхность стенки F за время τ:
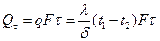 (31)
(31)
Если необходимо учитывать, зависимость λ от температуры и известна функция λ = λ(t), то в расчетные уравнения вводится среднеинтегральное значение λср., т.е.
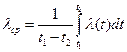 (32)
(32)
Дата добавления: 2016-01-18; просмотров: 809;
