Дифференциальное уравнение теплопроводности. Из закона Фурье следует, что для определения количества теп­лоты, проходящего через какую-либо поверхность твердого тела

Из закона Фурье следует, что для определения количества теп­лоты, проходящего через какую-либо поверхность твердого тела, не­обходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля является главной задачей аналити­ческой теории теплопроводности.

Выведем дифференциальное уравнение теплопроводности, которое дает описание температурного поля в рассматриваемом теле.

При выводе уравнения сделаем следующие попущения:

-тело однородно и изотропно;

-физические параметры постоянны;

-изменение объема, связанное с изменением температуры, мало по сравнению с самим объемом и им можно пренебречь;

-внутренние источники теплоты в теле распределены равномерно.

В основу вывода дифференциального уравнения теплопроводнос­ти положим уравнение первого закона термодинамики, который мо­жет быть сформулирован следующим образом: количество теплоты, введенной в элементарный объем извне за время dτ посредством теплопроводности, а также от внутренних источников тепла, равно изменению внутренней энергии вещества, содержащегося в элемен­тарном объеме:

, (15)

где dQ₁, Дж - количество теплоты, введенное в элементарный объем путем теплопроводности за время dτ;

dQ₂, Дж - количество теплоты, которое за время dτ выделилось в элементарном объеме за счет внутренних ис­точников тепла;

dU, Дж - изменение внутренней энергии вещества, содержащегося в элементарном объеме за время dτ.

Для нахождений составляющих уравнения (15) выделим в теле элементарный параллелепипед со сторонами dx, dy, dz (рис. 2). Параллелепипед расположен так, что его грани парал­лельны координатным плоскостям.

Количество теплоты, которое подводится к граням элементар­ного объема за время dτ в направлении осей Ox, Oy, Oz обозначим соответственно dQ_x, dQ_y, dQ_z.

Количество теплоты, которое будет отводиться через проти­воположные грани в тех же направлениях, обозначим соответственно dQ_x+dx, dQ_y+dy, dQ_z+dz.

Тогда количество тепло­ты, подведенное к грани dydz за время dτ, составляет:

,

где q_х - проекция плотности теплового потока на ось Ox. Количество теплоты, отведенное через противоположную грань в на­правлении оси Ох:

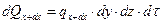
Z

Y

X

Pиc.2. К выводу дифференциального уравнения теплопроводности

Разница между количеством теплоты, подведенной к элементар­ному объему, и количеством теплоты, отведенной от него за время dτ в направлении оси Ох равно:

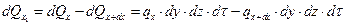
Функция q_х+dx является непрерывной в рассматриваемом интервале dx и может быть разложена в ряд Тейлора:

Поскольку записанный ряд является быстро сходящимся, то с достаточной степенью точности можно ограничиться двумя первыми членами ряда.

Тогда получим:

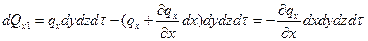
Аналогично найдем количество теплоты, подведенное к элементарному объему за вычетом отведенного в направлении оси Оy и Oz.

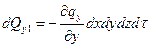
Тогд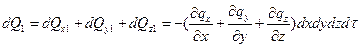а

(а)

Определим dQ₂ в уравнении (15). Обозначим количество тепло­ты, выделяемое внутренними источниками в единице объема тела в единицу времени q_v Вт/м³. Величину q_v называют мощностью внутренних источников тепла или объемной плотностью тепловыде­ления внутренних источников. Примерами внутренних источников тепла могут служить: выделение джоулевой теплоты при прохожде­нии электрического тока в теле, протекание химических реакций с выделением тепла (положительное значение q_v); химические ре­акции с поглощением тепла, испарение влаги внутри материала (от­рицательные значения q_v) и т.д.

С учетом введенного понятия q_v:

(б)

Правую часть уравнения (15) dU - изменение внутренней энергии найдем по выражению

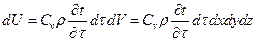(в)

где Cv - массовая изохорная теплоемкость, Дж/кгК;

ρ - плотность вещества, кг/м³;

dv = dхdydz - элементарный объем;

∂t/∂τ*dτ - изменение температуры в элементарном объеме за время dτ.

При составлении уравнения (15) было принято, что подвод теплоты осуществляется при V = const, при этом теплота идет на изменение внутренней энергии. Если принять, что подвод теп­лоты осуществляется при p = const, то тогда теплота пойдет на изменение энтальпии вещества dH, которая должна быть записана в правой части уравнения (15). Выражение для нахождения изменения энтальпии dH будет отличаться от (г) только теплоемкостью, вместо изохорной теплоемкости С_v там будет стоять изо­барная теплоемкость С_p.

Поскольку в твердых телах и капельных жидкостях разность между С_p и C_v мала, то можно принять С_p = C_v = C

С учетом последнего подставим (а), (б) и (в) в уравнение (15):

,

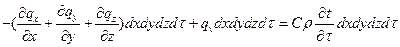Отсюда

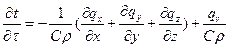(г)

По уравнению (12) имеем:

, ,

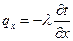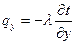Подставив эти выражения в уравнении (г ) получим дифференциальное уравнение теплопроводности

(16)

Уравнение (16) является дифференциальным уравнением теплопроводности в однородном неподвижном теле, выражающем зависимость температуры любой точки его от координат и времени или иначе устанавливающим связь между временным и пространственным изменениями температуры в любой точке тела, в котором происходит про­цесс теплопроводности.

В уравнении (16) обозначим

, [ ]

где а - коэффициент температуропроводности. Коэффициент а является физическим параметром вещества и характеризует теплоинерционные свойства вещества, т.е. скорость изменения температуры в теле. Материалы, способные быстро изменять свою темпера­туру в процессе нагрева или охлаждения, имеют высокие значения коэффициента температуропроводности, и наоборот. Очевидно, этот коэффициент является важнейшей характеристикой при описании не­стационарных процессов теплопроводности.

Далее обозначим:

,

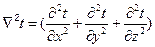где 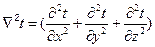- оператор Лапласа в декартовой системе координат. С учетом принятых обозначений уравнение (16) принимает вид:

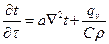(17)

При отсутствии в теле внутренних источников тепла (q_v = 0) уравнение (17) запишется:

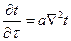(18)

Дифференциальное уравнение теплопроводности нужно уметь записывать для различных температурных полей. Например, если поле будет нестационарным, то уравнение (18) принимает вид:

Для одномерного нестационарного поля:

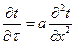
Самый простой вид уравнение принимает для одномерного ста­ционарного поля. В этом случае:

, ,

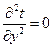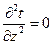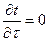
Поделив на а левую и правую честь уравнения (18) при названных условиях, получим уравнение:

Дифференциальное уравнение теплопроводности в цилиндрической системе координат с внутренними источниками тепла имеет вид:

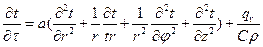, (19)

где r - радиус - вектор;

φ - полярный угол;

z - аппликата.