Плотность теплового потока.
Закон Фурье - основной закон распространения тепла теплопроводностью, который вначале был известен как гипотеза Фурье, а позднее получил статус закона. Согласно этому закону количество теплоты dQτ , проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту ∂t/∂n:
, 
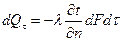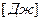(7)
Коэффициент пропорциональности λ в уравнении (7) есть физический параметр вещества, который характеризует способность вещества проводить теплоту и называется коэффициентом теплопроводности,
Количество теплоты, проходящей в единицу времени через изотермическую поверхность dF , называется тепловым потоком:
, 
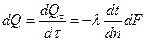(8)
Количество теплоты, проходящее в единицу времени через единицу пути изотермической поверхности, называется плотностью теплового потока
, 
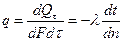(9)
Плотность теплового потока является векторной величиной. За положительное направление вектора плотности теплового потока q принимают направление по нормали к изотермической поверхности в сторону убывания температуры. Таким образом, векторы q и gradt, лежат на одной прямой, но направлены в противоположные стороны, что и объясняет наличие знака "минус" в правых частях уравнений (7), (8) и (9).
Таким образом, уравнения (7), (8) и (9) представляют закон Фурье, записанный соответственно для всего тепла, для теплового потока и для плотности теплового потока.
Закон Фурье в интегральной форме запишется для всего тепла, прошедшего за время τ через изотермическую поверхность F:
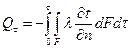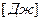, (10)
Для теплового потока
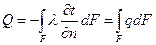, (11)
Если вектор плотности теплового потока спроектировать на координатные оси Ox, Oy, Oz , то согласно уравнению (6) получим:
, 
, 
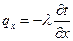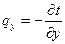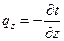. (12)
Дата добавления: 2016-01-18; просмотров: 791;