Апостериорная плотность вероятности

В задаче оценки параметра самой простой моделью сигнала является представление сигнала в виде квазидетерминированного колебания S(t, 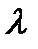), у которого известна функциональная зависимость от времени, но неизвестен какой-то параметр 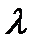(например, амплиту­да, частота или фаза). Этот параметр рассматривается как случай­ная величина с заданной априорной вероятностью р( 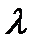), характери­зуемой большой дисперсией.

При решении задачи оценки параметра будем считать, что под­лежащий наблюдению процесс 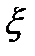(t) представляет собой сумму сигнала S(t, 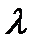) и шума n(t) с теми же характеристиками, что и в (5.1):

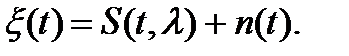
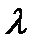Отличие от (5.1) состоит в том, что здесь уже установлено наличие сигнала. Требуется только за счет наблюдения реализации x(t) процесса (t) уточнить значение параметра . Условная плот­ность вероятности при непрерывном наблюдении реализации x(t), когда n(t) является гауссовским белым шумом, согласно (5.12) будет

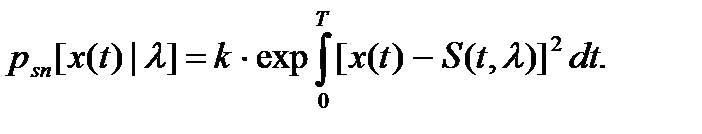(5.20)

Отличие (5.20) и (5.12) состоит только в том, что в силу неизвестности параметра 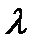, плотность вероятности (5.20) рассмат­ривается как условная относительно 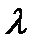. При этом задача оценки параметра сигнала, по существу, сводится к задаче оценки параметра распределения.

Если рассматривать x(t) в формуле (5.20) как результат наблюдения, то функция правдоподобия оцениваемого параметра пол­ностью будет совпадать с выражением (5.20);

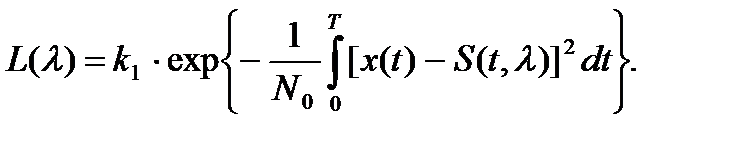(5.21)

и можно записать апостериорную плотность вероят­ности параметра 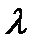в виде

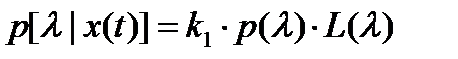(5.22)

где 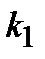находится из условия нормировки апостериорной плотности.

Основное свойство апостериорной плотности вероятности (5.22) состоит в том, что она содержит все сведения об оценивае­мом параметре 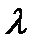, как имеющиеся до наблюдения x(t) в априорной плотности вероятности р( 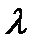), так и сведения, полученные в резуль­тате наблюдения x(t) и содержащиеся в функции правдоподобия L( ).

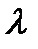6 ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ ФИЛЬТРЫ СИГНАЛОВ

НА ФОНЕ ПОМЕХ