Нормализация случайных процессов в узкополосных системах

Поставим задачу определить одномерную плотность вероятности 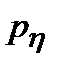(t) на выходе линейной системы, если известна одномерная плот­ность вероятности 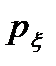(х) случайного процесса на входе и определена импульсная характеристика системы h(t), длительность огибающей которой характеризуется постоянной времени 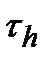(рис.4.3). Отличие 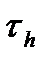от нуля соответствует инерционной линейной системе. Для цепи первого порядка 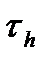совпадает с постоянной времени цепи.

Рис 4.3

Связь между 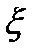(t) и (t) определяется выражением (4.8), ко­торое для удобства получения выводов запишем в дискретной форме, заменив интеграл суммой:

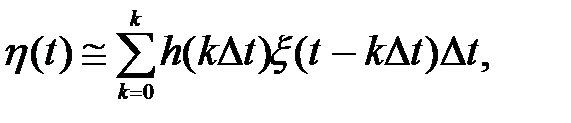(4.24)

где t - малый по сравнению с 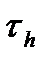интервал времени, определяющий шаг дискретизации;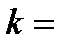 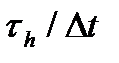число всех дискретных отчетов в течение времени 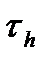, когда огибающая h(t) отлична от нуля.

Рассмотрим три случая.

1. Пусть процесс 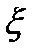(t) является гауссовским. В этом случае согласно (4.24) случайный процесс (t) представляется в виде суммы гауссовских величин 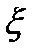( 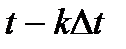), каждая из которых умножается на детерминированный множитель 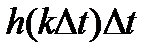. Из теории вероятностей известно, что сумма гауссовских величин есть гауссовская величина. Это означает, что при гауссовском входном процессе 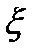(t) процесс на выходе (t) тоже является гауссовским, но с характеристиками, отличными от характеристик 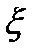(t). Например, 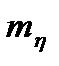(t) и 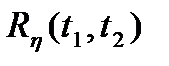определяются формулами (4.7) и (4.13).

Таким образом, линейная система инвариантна по отношению к гауссовскому распределению, то есть она сохраняет закон распреде­ления процесса на выходе, если на входе действует гауссовский процесс. Линейная система в результате преобразования входного процесса только изменяет его числовые характеристики.

2. Случайный процесс 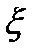(t) распределен по произвольному зако­ну, но его интервал корреляции 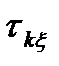весьма мал по сравнению с дли­тельностью переходной характеристики системы:

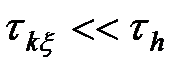. (4.25)

В этом случае согласно (4.24), если выбрать 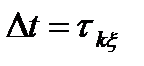, выход­ной процесс (t) можно рассматривать как сумму некоррелированных случайных величин 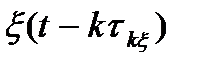, имеющих одно и то же распределение, причем каждое слагаемое суммы дополнительно умножается на детер­минированный множитель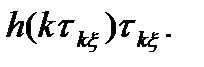

Здесь важно то, что из-за выполнения условия (4.25) число слагаемых в сумме (4.24) весьма велико, так как

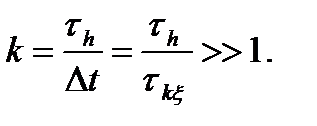(4.26)

Из теории вероятностей согласно центральной предельной тео­реме известно, что сумма большого числа независимых слагаемых с одним и тем же законом распределения имеет гауссовское распределение. Это означает, что если независимость слагае­мых приближенно заменить их некоррелированностью, то процесс (t) будет стремиться иметь гауссовское (нормальное) распределение тем точнее, чем сильнее будет выполняться условие (4.25). В этом проявляется суть нормализации случайных процессов инерционными системами.

Этот же вывод можно сформулировать на частотном языке. Учи­тывая, что длительность переходной характеристики 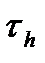обратно про­порциональна полосе пропускания цепи 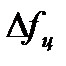, а интервал корреляции входного процесса 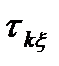обратно пропорционален эффективной ширине спектра этого процесса 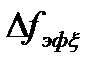, условие (4.25) можно записать в виде

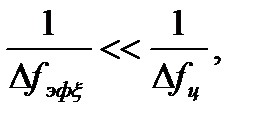
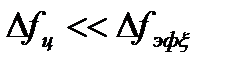. (4.27)

Таким образом, если линейная система или электрическая цепь является узкополосной по отношению к входному процессу, то закон распределения случайного процесса на выходе системы приближается к гауссовскому закону тем точнее, чем сильнее выполняется условие узкополосности (4.27).

3. Если плотность вероятности входного процесса 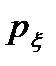(x) отлич­на от гауссовского и условие узкополосности линейной системы не выполняется, то в общем случае сделать вывод о распределении вы­ходного процесса нельзя. Необходимо исследовать выражение (4.24) для конкретного выходного процесса и конкретной линейной системы.