На выходе линейной системы

В радиотехнике широкое распространение находит спектральный метод анализа прохождения колебаний через линейные системы. В этом случае основной характеристикой линейной системы является её комплексная частотная характеристика 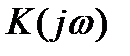. При известной 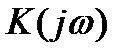и заданном спектре воздействия 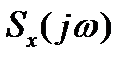спектр отклика находится как произведение

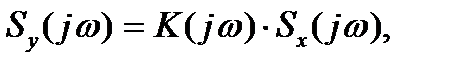(4.16)

где 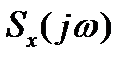, , 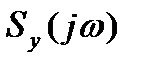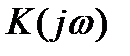являются соответственно преобразованиями Фурье воздействия х(t), отклика у( t ) и импульсной характерис­тики системы h(t).

При анализе линейных цепей под детерминированными временными зависимостями x(t), y(t) понимаются напряжения или токи, так что 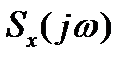, 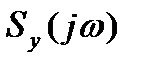- их соответствующие комплексные спектры. Если же для x(t), y(t) рассматривать энергетические спектры 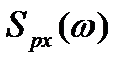, , 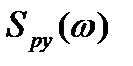определяющие, в зависимости от частоты, среднюю за период мощность спектральных составляющих, отнесенную к единичной полосе частот, то выражение (4.16) для энергетических спектров примет вид

(4.17)

где 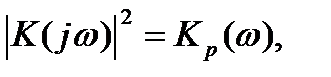- квадрат модуля комплексной частотной характе­ристики, определяющий частотную характеристику цепи по мощности.

Заметим, что все частотные функции в формуле (4.17), то есть 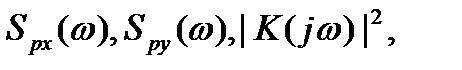являются не комплексными, а дейст­вительными неотрицательными функциями.

Если воздействие является случайным процессом 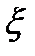(t), то от­клик (t) также будет случайным. Так как спектральные плотности процессов 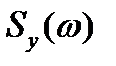, 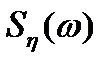являются функциями частоты, определяющими среднюю мощность флюктуации, отнесенную к единичной полосе час­тот, то формула (4.17) будет справедлива и в этом случае. Для стационарных случайных процессов на входе и выходе линейной сис­темы она примет вид

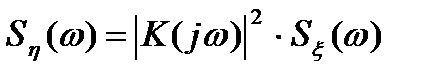. (4.18)

Строгий математический вывод формулы (4.18) основан на вы­числении преобразования Фурье корреляционной функции стационарно­го случайного процесса, определяемой выражением (4.14) с учетом формулы (4.15).

Если используется частота f, aспектральные плотности опре­делены для 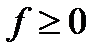, то формула (4.18) запишется в виде

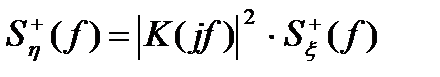. (4.19)

Если входным процессом является белый шум n(t) со спектральной плотностью N₀, то

. (4.20)

Из выражения (4.20) следует, что спектральная плотность выходного процесса при белом шуме на входе пропорциональна квад­рату модуля комплексной частотной характеристики линейной систе­мы.

Введем нормированную комплексную частотную характеристику

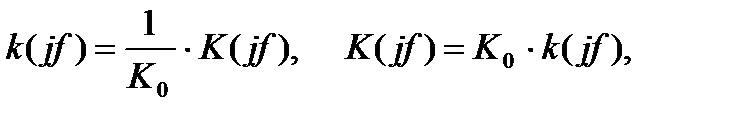(4.21)

где K₀ - максимальное значение характеристики на какой-то опреде­лённой частоте, например на f = 0.

Найдем дисперсию выходного процесса (t), когда на входе ли­нейной цепи действует белый шум.

(4.22)

В формуле (4.22) интеграл по всем положительным частотам от квадрата нормированной комплексной частотной характеристики цепи определяет шумовую полосу 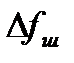этой цепи

(4.23)

Физический смысл 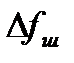поясняется рис. 4.2. Шумовая полоса 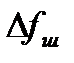определяет при белом шуме на входе эффек­тивную ширину спектральной плотности выходного процесса. Это оз­начает, что если реальную спектральную плотность 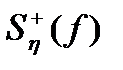заменить прямоугольной с высотой и основанием прямоугольника, соответст­венно равными N₀K₀² и 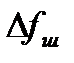, то дисперсия на выходе процесса будет в обоих случаях одинакова (рис. 4.2, а). При использовании нормиро­ванной 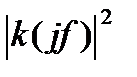это соответствует тому, что площадь прямоугольни­ка с высотой и основанием, равными соответственно 1 и 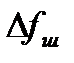, равна площади под кривой 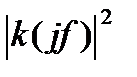для .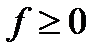

Рис. 4.2