II. Элементы линейной алгебры
§ 1. Матрицы и определители [3, 7]
Определение. Матрицей размера m´n называется совокупность m×n элементов, представленная в виде таблицы, состоящей из m строк и n столбцов
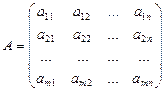 ,
,
где 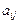 – элемент матрицы A, стоящий на пересечении i-ой строки и j-го столбца,
– элемент матрицы A, стоящий на пересечении i-ой строки и j-го столбца, 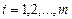 ,
, 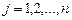 ,
, 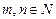 .
.
Матрица размера 1´n или m´1 называется матрицей-строкой или матрицей-столбцом соответственно (или вектором).
Если число строк матрицы равно числу столбцов, то матрица называется квадратной, а число строк называется ее порядком или размером. Матрица A порядка n имеет вид:
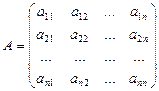
Элементы квадратной матрицы размера n, стоящие на пересечении строк и столбцов с одинаковыми номерами, то есть 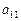 ,
, 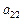 , …,
, …, 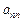 , образуют главную диагональ, а сумма элементов главной диагонали
, образуют главную диагональ, а сумма элементов главной диагонали 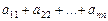 называется следом матрицы. Соответственно элементы
называется следом матрицы. Соответственно элементы 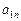 ,
, 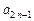 , …,
, …, 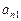 , лежащие на прямой, соединяющей правый верхний и левый нижний углы матрицы, образуют побочную диагональ.
, лежащие на прямой, соединяющей правый верхний и левый нижний углы матрицы, образуют побочную диагональ.
Мы будем рассматривать числовые и функциональные матрицы.
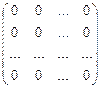
Определение. Матрица, все элементы которой равны нулю, называют нулевой.
Определение. Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю, называется единичной и обозначается
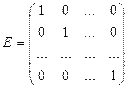
Определение. Квадратная матрица, у которой элементы, расположенные ниже главной диагонали, равны нулю, называется треугольной.
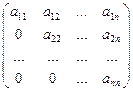
Определение. Матрица АТ называется транспонированной к матрице A, если у нее каждая строка является столбцом матрицы A с тем же номером.
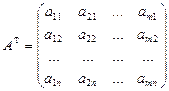
Дата добавления: 2016-01-26; просмотров: 2530;
