Приближенные вычисления

Множество действительных чисел R широко применяется в математике и ее приложениях. В инженерных расчетах обычно конечный результат представляют в виде десятичной дроби. Но не каждое действительное число может быть точно записано в таком виде. К ним относятся все рациональные с периодом и все иррациональные числа. Их приходится округлять, то есть записывать приближенно. Для того, чтобы иметь n точных знаков после запятой, нужно вычислить не менее чем n+2 знака (т.е. дополнительно 2 разряда) и округлить по известным правилам.

Следует иметь в виду, что если приходится суммировать очень много слагаемых, то накапливается ошибка. Пренебрежение правилами округления, а иногда и при округлении с любой точностью, можно получить принципиально неверный результат. Особенно актуальна проблема оценки ошибок вычисления при нахождении корней уравнений и решения систем уравнений. Например, система уравнений 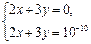не имеет решений (система несовместна), а при округлении правой части второго уравнения 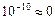система 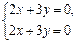имеет множество решений.

При нахождении корней уравнения 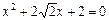любое округление в сторону уменьшения 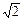приводит к отсутствию действительных корней.