Вычисление определителей
Определитель 2-го порядка равен разности произведений элементов главной и побочной диагоналей, то есть
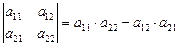 .
.
Пример II.2.Вычислить определители:
1). 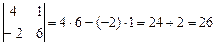 ;
;
2). 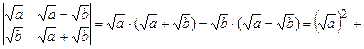
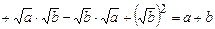 ;
;
3). 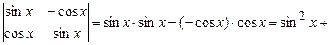
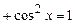 .
.
Определитель 3-го порядка вычисляется по формуле:
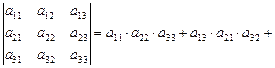
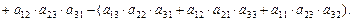 (II.1)
(II.1)
Для запоминания используется мнемоническое правило – правило треугольников. Оно состоит в изображении (явном или мысленном) элементов матрицы точками. Точки, соответствующие произведениям, которые входят в формулу определителя, соединяются отрезками.
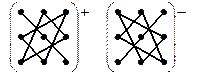
Главной диагонали и двум треугольникам, основания которых параллельны главной диагонали, соответствуют произведения со знаком “+”, а побочной диагонали и треугольникам, основания которых ей параллельны, соответствуют произведения со знаком “-”.
Определение. Минором k-го порядка матрицы порядка n называется определитель, полученный из исходного вычеркиванием n-k строк и n-k столбцов. Определитель, составленный из элементов, стоящих на пересечении вычеркнутых n-k строк и столбцов, называется дополнительным минором к минору k-го порядка, 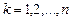 .
.
Определение. Минором 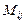 элемента
элемента 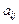 матрицы порядка n называется определитель порядка n-1, полученный вычеркиванием i-ой строки и j-го столбца из определителя D исходной матрицы. Элемент
матрицы порядка n называется определитель порядка n-1, полученный вычеркиванием i-ой строки и j-го столбца из определителя D исходной матрицы. Элемент 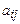 и его минор
и его минор 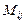 являются взаимнодополнительными минорами,
являются взаимнодополнительными минорами, 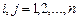 .
.
Определение. Алгебраическим дополнением 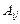 элемента
элемента 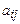 матрицы порядка n называется минор
матрицы порядка n называется минор 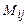 этого элемента взятый со знаком «+», если сумма i+j четная, и со знаком «-», если сумма i+j нечетная, то есть
этого элемента взятый со знаком «+», если сумма i+j четная, и со знаком «-», если сумма i+j нечетная, то есть
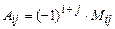 ,
, 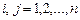 . (II.2)
. (II.2)
Определитель n-го порядка можно вычислить разложением по i-ой строке (j-ому столбцу). Например, для определителя 3-го порядка получаются следующие равенства:
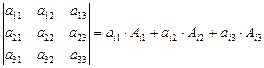 ,
, 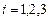
или
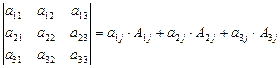 ,
, 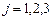 .
.
Пример II.3.
1).Вычислим определитель по правилу треугольников:
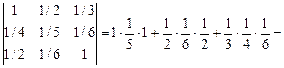
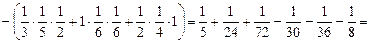
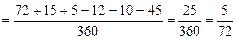 .
.
2).Вычислим определитель разложением по третьему столбцу. Определим алгебраические дополнения элементов третьего столбца:
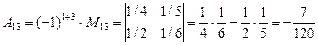 ,
,
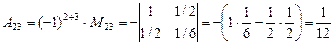 ,
,
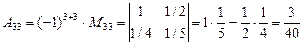 .
.
Далее, по формуле (II.2), имеем
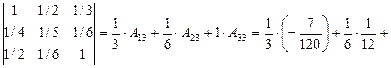
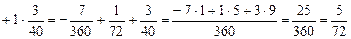 .
.
Дата добавления: 2016-01-26; просмотров: 1409;
