Вычисление апостериорных вероятностей
При решении задач оптимального приема ответ получается на основе предварительных (априорных) сведений о принимаемом сигнала и надлежащей обработке его.
Если бы мы не располагали предварительными сведениями о сигнале (т.е. о его параметрах), то его нельзя было бы отличить от помехи. Наоборот, прием детерминированного сигнала не доставляет никакой информации; если все о нем известно, то его всегда можно полностью воспроизвести на приемном конце. Поэтому носителями полезной информации могут быть только неизвестные параметры сигнала.
По сравнению с априорными сведениями, знание наблюдателя об исследуемой ситуации в результате анализа принятого колебания увеличивается. Вновь сформированное знание называется
апостериорным.
Вспомним элементы теории вероятностей. Вероятность совместного события
Р(А×В) = Р(А)×Р(В/А) = Р(В)×Р(А/В).
Известны: Р(Нk) и P(FA/Hk) ... P(B/Hn), Н1, Hk, Hn – гипотезы и передаче сигналов, Pa(Hk) – априорная их вероятность.
Найти Р(А) – безусловную вероятность.
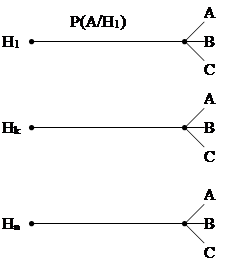 |
ΣР(Нk) = 1
Формула полной вероятности:
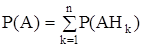 ,
,
т.к. Р(АHk) = P(Hk)×P(A/Hk)
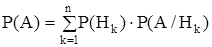 (5.1)
(5.1)
Если обратная задача: известно P(A) и P(A/Hk), то нужно найти, какая была Hk - это задача Байеса:
Р(АHk) = P(Hk)×P(A/Hk) = P(A)×P(Hk/A)
отсюда
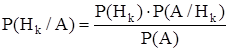 .
.
Р(А) из формулы полной вероятности
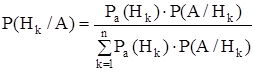 , (5.2)
, (5.2)
здесь Ра(Hk) – априорное (до опыта, до передачи сигнала) распределение вероятностей гипотез Hk;
Р(Hk/А) – апостериорная вероятность (после опыта, после приема сигнала), которую обозначим Ppst( ).
Пусть бинарный сигнал принимается на фоне аддитивной помехи в виде белого шума, т.е. стационарной помехи с энергетическим спектром постоянной интенсивности по всей оси частот y(t) = s(t) + n(t).
Для упрощения математических выкладок введем временно следующее ограничивающее условие: Принятая смесь y(t) перед последующей обработкой пропускается через фильтр нижних частот с прямоугольной АЧХ и ФЧХ ∆φ(ω) = 0. Обозначим полосу пропускания фильтра через ∆fф = 0 ... fв.
Пусть по каналу связи передается один из возможных сигналов мновества {S1, S2, ..., SL}. На приемном конце канала получена реализация y(t). В соответствии с теоремой Байеса вероятность того, что в принятой смеси находится сигнал Sk(t) равна
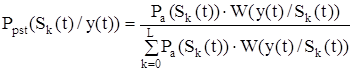 , (5.3)
, (5.3)
где Pa(Sk) - априорная вероятность передачи сигнала Sk(t)$
W(y(t)/Sk(t)) - плотность вероятности получения принятой реализации смеси при условии, что был передан сигнал Sk(t) .
Т.к. знаменатель выражения (1.1) не зависит от конкретного значения k, то
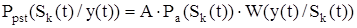 , (5.4)
, (5.4)
где А - постоянная, не зависящая от k величина.
Как будет показано ниже, для решения задачи различения символов небходимы не абсолютные значения апостериорных вероятностей, а соотношения между ними. Поэтому значение постоянной величины нас в дальнейшем интересовать не будет.
Таким образом, распределение апостериорных вероятностей передачи каждого из возможных сигналов (пауза в некоторых случаях также может рассматриваться как один из сигналов) при заданном распределении априорных вероятностей определяется только условными плотностями вероятностей W(y/Sk).
Пропущенная через фильтр низких частот смесь y(t), имеет ограниченный спектр, следовательно, функция W(y/Sk) в соответствии с теоремой Котельникова полностью определяется отсчетами, взятыми с интервалами ∆t = 1/2fв. Отсюда следует, что плотность вероятности W(y/Sk) есть m-мерная условная плотность, где m - количество отсчетов, определяющих функцию:
W(y/Sk) = W(y1, y2, ..., ym / Sk1, Sk2, ..., Skm) (5.5)
Рассматриваемая как функция k условная m-мерная плотность вероятности называется функцией правдоподобия. Обозначив ее через L(Sk), получаем:
Ppst(Sk/y) = A × Pa(Sk) × L(Sk) (5.6)
При заданном сигнале вероятности получения мгновенных значений смеси y1, y2, ..., ym, равны соответственно вероятностям мгновенных значений шума в эти же моменты времени n1, n2, ..., nm. Поэтому
L(Sk) = W(n1, n2, ..., nm).
Белый шум, пропущенный через фильтр с ограниченной полосой, является гауссовым стационарным процессом с автокорреляционной функцией вида R(τ) = sinωвτ/ωвτ. Следовательно, отсчеты шума, взятые с интервалами ∆t = 1/2fв между собой являются некоррелированными, а, значит, и независимыми. Поэтому, в соответствии с (5.5) L(Sk) равна произведению одномерных безусловных плотностей вероятности
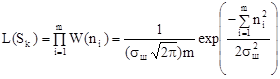 . (5.7)
. (5.7)
Т.к. дисперсия шума на входе фильтра σ2ш = N0∆fф = N0/2∆t, то
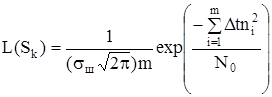 .
.
При отсутствии в принятом колебании y(t) сигнала, т.е. при yi = ni функция правдоподобия принимает вид:
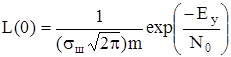 ,
,
где 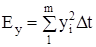 - энергия принятого колебания.
- энергия принятого колебания.
Отношение функций правдоподобия
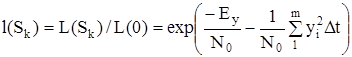 . (5.8)
. (5.8)
Предположение о наличии прямоугольного фильтра на входе устройства обработки было введено нами для того, чтобы получить выражение (5.7), ибо при белом шуме σ2ш = ∞ и выражение (5.7) не имеет смысла. Но уже в выражение (5.8) мощность шума не входит. Поскольку в дальнейшем мы будем пользоваться выражением (5.8), то предположение о наличии фильтра на входе теперь можно отбросить. При этом ∆fф = ∞ и выражение (5.8) преобразуется к следующему виду:
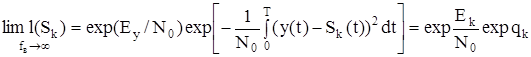 , (5.9)
, (5.9)
где 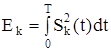 или для прямоугольного импульса Ek = A2 τu – энергия
или для прямоугольного импульса Ek = A2 τu – энергия
k-го сигнала
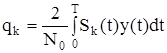 (5.10)
(5.10)
где Т - длительность реализации y(t).
Выражение (5.9) часто называют отношением правдоподобия, а qk – функционалом правдоподобия (корреляционный интеграл).
Определив отношение правдоподобия для всех сигналов алфавита источника, можно получить в соответствии с (5.6) распределение их апостериорных вероятностей.
Литература:
[1] стр. 149-160. [2] стр. 169-173. [3] стр. 163-168.
Контрольные вопросы:
1. В чем смысл теории Байеса?
2. Что отражает функция правдоподобия?
3. Поясните состав выражения функционала правдоподобия.
Дата добавления: 2016-01-18; просмотров: 2671;
