Задачи оптимального приема

ПРИЕМ И ОБРАБОТКА СИГНАЛОВ

Задачи оптимального приема

Теория передачи сигналов подразумевает теоретическое обоснование способов и методов передачи информации от источника к получателю с помощью какого-либо переносчика, в частности, радиосигнала. Радиосигнал, как носитель полезной информации, в канале связи от передатчика к приемнику претерпевает изменения, вызванные искажениями при передаче, влиянием помех в канале связи, искажениями при приеме. Если в точке передачи сигнала достаточно просто проконтролировать и откорректировать передаваемый сигнал с целью снижения искажения передатчика, то в точке приема приходится иметь дело с сигналом, искаженным каналом связи случайным образом и по не зависящим от нас обстоятельствам, что приводит к необходимости применять особые способы приема сигнала для снижения возможных ошибок в передаче информации (оптимальный прием сигналов).

Принимаемый сигнал имеет часть параметров, известных априорно (т.е. до передачи). Если известны все параметры сигнала, то нет смысла его принимать (он известен); если все параметры сигнала заранее неизвестны, то принять и выделить его на фоне помех не представляется возможным (неизвестно, что выделять). При малом объеме априорных данных необходимо пользоваться методами адаптивного приема.

Оптимальный (идеальный) прием сигналов, обеспечивающий минимальные искажения сообщения, реализуется оптимальный приемником, работающим по оптимальному алгоритму, основанному на априорной информации и выбранных критериях оптимальности.

Оптимальный приемник обеспечивает минимальный уровень искажений, который принято называть потенциальной помехоустойчивостью. По определению, помехоустойчивость реальных приемников не может превышать потенциальную для заданных условий, а только приближаться к ней. Сравнивая помехоустойчивость реальных приемников с потенциальной помехоустойчивостью, можно выяснить степень технического совершенства реальных приемников и возможные резервы повышения их помехоустойчивости. Сравнивая значения потенциальной помехоустойчивости при различных видах сигналов, можно определить наилучшие виды передаваемых сигналов.

Решение основных проблем теории оптимального радиоприема базируется на хорошо разработанных методах математической статистики, разработанных А.Н.Колмогоровым, Н.Винером, В.А.Котельниковым и др.

В зависимости от целевого назначения и условий работы различают четыре задачи, решаемых в теории оптимальных методов радиоприема.

Будем рассматривать аддитивную смесь сигнала и помехи:

y(t) = s(t, λ) + n(t),

где λ = λ{λ₁...λ_m} – параметры, от которых зависит сигнал;

n(t) – аддитивная помеха, в общем случае представляется моделью белого нормального центрированного шума (см. лекцию 1).

1. Обнаружение сигнала.

Пусть неизвестен сам факт наличия или отсутствия сигнала s(t, λ) в принятом колебании y(t), т.е.

y(t) = q s(t, λ) + n(t), 0 ≤ t ≤ T, q = 0; 1,

здесь q - случайная величина на два значения 0, 1.

Необходимо оценить значение дискретного параметра q. В результате решения должна быть получена структурная схема оптимального обнаружения сигнала и определены его количественные характеристики.

2. Различение сигналов.

Предположим, что в принятом колебании y(t) может быть только один из двух сигналов:

y(t) = q s₁(t, λ₁) + (1 - q) s₂(t, λ₂) + n(t), 0 ≤ t ≤ T.

Эта задача характерна для систем передачи бинарных сигналов, в частности, в телеграфии. Возможна постановка задачи для большего количества сигналов (радиосвязь, телеуправление).

3. Оценка параметров сигнала.

Пусть какой-нибудь параметр х_i сигнала s(t, λ) является случайной величиной с априорной плотностью вероятности P_opr(x_i). Необходимо с минимальной погрешностью определить значение этого параметра λ_i в принятой реализации y(t). Это простейшая задача оценки параметров сигнала. Возможна постановка задачи о совместной оценке двух и более параметров. Такие задачи характерны для измерительной техники, радиолокации, радионавигации.

4. Фильтрация сообщений.

Пусть интересующий нас параметр λ_i полезного сигнала s(t, λ) зависит от времени и представляет собой информационное сообщение – случайный процесс λ_i(t) с известными статистическими характеристиками. Располагая сведениями о помехе n(t), нужно получить (отфильтровать, выделить наилучшим образом) оценку 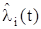реализации случайного сообщения λ_i(t), содержащейся в наблюдаемой реализации y(t).

Задача фильтрации переходит в задачу оценки параметра сигнала, если оцениваемый параметр за время наблюдения Т не успевает существенно измениться.

Задачи фильтрации возникают в радиосвязи и телеметрии (выделение речевого или какого-либо другого сообщения), в телевидении (выделение телевизионного сообщения) и т.д.

Литература:

[1] стр. 149-150. [2] стр. 165-169. [3] стр. 159-163.

Контрольные вопросы:

1. Что понимают под оптимальным приемом?

2. Можно ли принимать сигнал при априорной неопределенности (если о нем ничего не известно)?

3. Какие задачи решает оптимальная обработка сигналов?