Вычисление количества света, падающего на фотоприемник

Чтобы как следует себе представить «световой вопрос» с точки зрения камеры, нам нужно знать, какое количество света действительно падает на фотоприемник.

Величина освещенности на ПЗС‑матрице (ИС на ПЗС) (или лицевой панели) Е_пзс в первую очередь зависит от яркости объекта L, а также от F‑числа, т. е. собирающей способности линзы. Чем ниже F‑число, тем больше света проходит через объектив (ниже мы еще рассмотрим этот вопрос). Эта величина также пропорциональна коэффициенту пропускания объектива т. А именно, в зависимости от качества стекла и производителя, а также от механики внутренних поверхностей, определенный процент света теряется в самом объективе.

Все вышеупомянутые факторы можно представить следующим соотношением:

Е_пзс = L∙τ∙π/4∙F²) [лк] (11)

Ниже мы покажем, как выводится это соотношение, чтобы люди, используя эти формулы, могли четко понимать, что здесь предполагается, а что аппроксимируется (11). Но поскольку для этого требуются более сложные математические выкладки, то читатели, не испытывающие к этому интерес или не имеющие соответствующей базы, могут просто воспользоваться соотношением (11) как оно есть, помня при этом, что L – это средняя яркость объекта (в люксах), – это коэффициент пропускания объектива (в процентах), F– это F‑число и равно 3.14.

Объект, находящийся в поле зрения камеры и освещенный источником света, испускает свет практически во всех направлениях, в зависимости от функции отражения. На практике объект с гладкими поверхностями в большинстве случаев может считаться ламбертовской равномерно рассеивающей поверхностью.

Тогда можно рассматривать поток, проходящий через полусферу радиуса r с центром ds . Пусть dθ – это приращение угла θ к нормали, тогда поток в объеме, образованном вращением угла dθ проходит через окружность на поверхности сферы, причем радиус окружности равен r dθ , длина – 2π∙r²∙sinθ∙dθ .

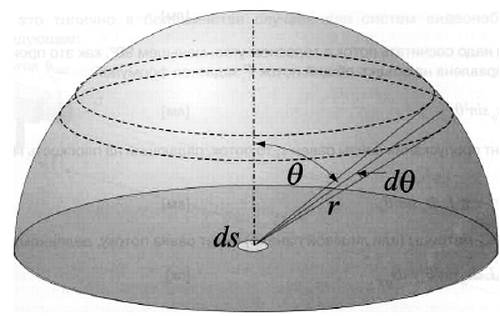
Рис. 2.10. Ламбертовская рассеивающая поверхность

Эта элементарная площадка на поверхности сферы задается следующим соотношением:

dA = 2π∙r²∙sinθ∙dθ (12) и тогда телесный угол ω , стягиваемый конусом в центре сферы, задается соотношением:

ω = dA/r² = 2π∙r²∙sinθ∙dθ/r² = 2π∙sinθ∙dθ [стерадиан] (13)

поскольку сила света на ламбертовской поверхности (поток в стерадиане) в заданном направлении пропорциональна косинусу угла к нормали, а сила света полной поверхности в направлении нормали равна I , то под углом θ она будет равна I∙cosθ

Сила света dI элементарной площадки ds равна:

dI = I∙cosθ∙ds /s [люмен/стерадиан = кандел] (14)

поскольку I/s это действительная освещенностьL в перпендикулярном направлении, то вышеприведенное соотношение принимает вид:

dI = L ∙cosθ∙ds [кд] (15)

Элементарный поток dF равен элементарной силе света dI , помноженной на телесный угол:

dF = L ∙cosθ∙ds∙2π∙sinθ∙dθ [лм] (16)

Общий поток в конусе, образованном углом θ можно найти интегрированием от 0 до θ :

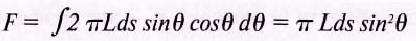
[лм] (17)

Если мы хотим найти полный световой поток, испускаемый во всех направлениях, то нужно положить угол θ равным 90°, тогда получим:

F_t = L∙π∙ds [лм] (18)

Теперь, если нам надо сосчитать поток в телесном угле, меньшем 90°, как это происходит в случае, когда камера направлена на объект, общий поток F_t задается формулой:

F₀ = π∙L∙ds₀∙sin²θ₀ [лм] (19)

Если коэффициент пропускания линзы равен τ , то поток, падающий на плоскость ПЗС (или лицевую панель), равен:

F_ПЗС = F₀∙τ = τ∙π∙L∙ds_0∙sin²θ₀

Освещенность ПЗС‑матрицы (или лицевой панели) будет равна потоку, деленному на площадь, т. е.

E_ПЗС = τ∙π∙L∙ds₀∙sin²θ₀/ds_ПЗС [лк] (21)

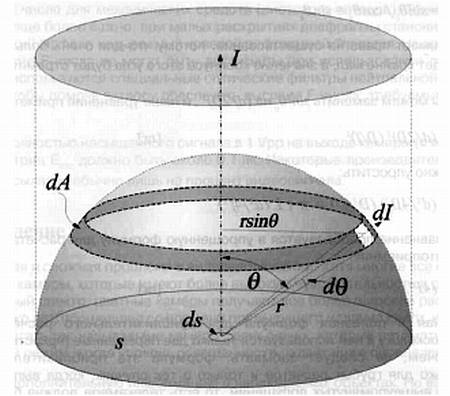
Рис. 2.11 . Вычисление светового излучения с помощью ламбертовской рассеивающей поверхности

Отношение (ds_ПЗС/ds₀₎, обратное которому использовалось в предыдущей формуле, известно как коэффициент увеличения объектива m . Коэффициент увеличения может быть также аппроксимирован как отношение между фокусным расстоянием линзы и расстоянием от линзы до объекта

m = (f/D)² = ds_ПЗС/ds₀ (22)

Когда мы произведем подстановку этих отношений в нашу основную формулу, то получим:

E_ПЗС = π∙τ∙L∙sin²θ₀∙(D/f)² [лк] (23)

Здесь потребуется ввести еще одно отношение, связанное с объективом (d/f), которое также известно как F‑число объектива. Для объектов, которые расположены достаточно далеко от телекамеры (а это типично в большинстве случаев для систем видеонаблюдения) будет справедливо следующее:

tgθ₀ = d/2D = sinθ₀/cosθ₀ = sinθ₀ (24)

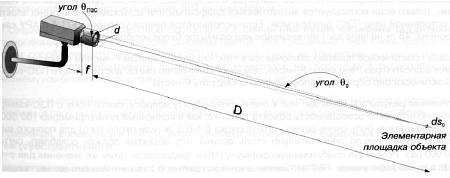
Рис. 2.12 . Вычисление количества света, падающего на ПЗС‑матрицу

Такое допущение имеет право на существование, потому что для очень больших расстояний до объекта угол θ₀ будет крайне мал, а значение косинуса этого угла будет стремиться к 1.

Таким образом, мы можем заменить sin²θ₀ на (d/2D)² , и наше уравнение примет следующий вид:

E_ПЗС = π∙τ∙L∙ (d/2D)²∙(D/f)² [лк] (25)

Это уравнение можно упростить:

E_ПЗС = π∙τ∙L∙ (d²/4D²)∙(D²/f²) = π∙τ∙L∙(d²/4f²) (26)

И, наконец, это уравнение преобразуется в упрощенную формулу для расчета количества света, попадающего в фотоприемник:

E_ПЗС = π∙τ∙L∙(4F²) [лк] (27)

Это очень удобная и полезная формула для приблизительного расчета освещенности фотоприемника, поскольку в ней используется только две переменные (яркость объекта и F‑число объектива). Впрочем, не следует забывать: формула эта приблизительная, ее следует использовать только для грубых расчетов и только в тех случаях, когда выполняются условия, справедливые для вышеупомянутых допущений, то есть телекамера должна быть направлена на объект, рассеивающий свет примерно так же, как ламбертовская рассеивающая поверхность (в реальности так ведут себя большинство объектов, кроме зеркал и им подобных поверхностей), а сам объект должен быть расположен достаточно далеко (по сравнению с фокусным расстоянием) от телекамеры. Обычно коэффициент пропускания объектива меняется в пределах от 0.75 до 0.95.

Если производитель его не указывает, то для вычислений можно принимать значение 0.8.

Давайте рассмотрим пример. Пусть освещенность плоскости объекта составляет около 300 лк, как примерно в любом помещении офиса (пусть это будет E_object), яркость можно найти, используя коэффициент отражения окружающих объектов, т. е.L = E_object·р . Как уже упоминалось выше, различные объекты имеют различные коэффициенты отражения, но мы не далеко уйдем от реальности, если примем его равным 50 % для условий офиса. Если диафрагма объектива установлена на F/16, то освещенность ПЗС‑плоскости будет составлять приблизительно Е_пзс= 0.8–3.14 – 300∙0.5/(4 – 256) = 0.З блк. Это вместе с АРУ (AGC) камеры вполне реалистичная освещенность плоскости ПЗС‑матрицы полного видеосигнала. Если же диафрагма объектива установлена на F/1.4, например, то освещенность ПЗС‑плоскости будет равна примерно 48 лк (согласно соотношению (17)). Это значение гораздо выше необходимого для ПЗС‑матрицы, и на практике она может дать узнаваемое изображение, только если используется автоустановка диафрагмы или если камера снабжена электронной встроенной (или ПЗС) диафрагмой. Если используется ручная установка F/1.4 и АРУ камеры отключена, 48 лк на чипе даст интенсивное или размытое белое изображение.

Базовое практическое правило заключается в том, что даже с низким F‑числом объектив ослабляет свет в десятки раз. Чем выше F‑число, тем ниже количество света, достигающего ПЗС‑плоскости. Фактически оно обратно пропорционально квадрату F‑числа.

Полученные результаты приводят нас к очень интересному вопросу, связанному с ПЗС‑камерами (особенно ч/б): если освещенность объекта такая же, как в солнечный день (примерно 100 000 лк), то F‑число должно быть очень велико. Это порядка 0.1–0.3 лк (или около того) для полного видеосигнала. Такое F‑число действительно столь велико, что объектив должен ослаблять сигнал в 1 000 000 раз. Используя приближенную формулу (16) и предполагая такие же значения для τ = 0.8 и р = 0.5, а также имея в виду, что ПЗС‑матрица камеры требует 0.2 лк на 1 Vpp сигнал, мы получим F‑число, равное 886.

Это очень большое число для механических средств (листового затвора). Точность его движения ограничена, и, что еще более важно, при малых раскрытиях диафрагмы становится заметен нежелательный оптический эффект, называемый краевой рефракцией Френеля. На практике это означает, что очень высокие F‑числа не могут быть достигнуты при использовании лишь механических методов. Поэтому используются специальные оптические фильтры нейтральной плотности (neutral density filter, ND ), чтобы помочь затвору обеспечить высокие F‑числа, требуемые для чувствительных ПЗС‑матриц.

Для обеспечения полностью насыщенного сигнала в 1 Vpp на выходе камеры (с отключенной АРУ) в случае ч/б ПЗС‑матриц Е_пзс должно быть около 0.1 лк. Некоторые производители приводят более низкие значения, ссылаясь обычно лишь на процент видеосигнала.

Цвет и телевидение

Цвет – очень важная и сложная проблема в видеонаблюдении. Хотя многие все еще предпочитают монохромные (ч/б) камеры, которые имеют более высокую чувствительность и реагируют на невидимый инфракрасный спектр, цветные камеры получают все более широкое распространение. За последние несколько лет, прошедшие со времени предыдущего издания книги, немало производителей стали предлагать так называемые камеры «день/ночь», которые автоматически переключаются в черно‑белый режим, когда уровень освещенности падает ниже определенного значения.

Цвет дает ценную дополнительную информацию о наблюдаемых объектах. Но важнее то, что человеческий глаз фиксирует цветовую информацию быстрее, чем мелкие детали объекта. Впрочем, недостатком цветных телекамер были худшие (по сравнению с черно‑белыми телекамерами) эксплуатационные показатели в условиях слабой освещенности. Это связано с использованием инфракрасного отсекающего фильтра на ПЗС‑матрицах цветных телекамер, который ослабляет свет и убирает невидимое излучение инфракрасного диапазона. На этом мы остановимся более подробно в соответствующей главе, посвященной телекамерам, а сейчас отметим, что постоянное усовершенствование технологии ПЗС значительно улучшает работу цветной камеры при минимальном освещении. Если еще несколько лет назад мы имели показатель 10 лк @ F1.4, то сегодня могут «видеть» при 1 лк @ F1.4 на объекте и даже меньше.

Как уже говорилось, цвета, которые мы видим, соответствуют волнам света разной длины.

Например, видимый нами красный цвет – это излучение с соответствующими длинами волн, отраженное от красного объекта, на который падает белый свет. Черный поглощает волны почти любой длины, тогда как белый большинство из них отражает.

Наука цветов очень сложна, и становится еще сложнее, когда окружающие нас естественные цвета воспроизводятся при помощи покрытия ЭЛТ люминофором.

Идея создания цветов в телевизоре заключается в смешении путем сложения (аддитивном) соседних люминесцентных точек трех основных цветов. Эти крошечные точки очень малы и представляют собой элементы маски экрана ЭЛТ‑монитора. Такая же концепция используется и при смешивании цветов в плазменных панелях и ЖК‑мониторах, но, поскольку в видеонаблюдении по‑прежнему наиболее распространены ЭЛТ‑мониторы, мы детально рассмотрим именно их.

Фактическое смешивание цветов происходит тогда, когда мы смотрим на монитор с нормального расстояния (в пару метров), и глаз воспринимает итоговый цвет каждой из этих трех точек.

Для сравнения, в живописи и печати цвета получаются в результате смешения путем вычитания цветов (субстрактивного).

При аддитивном смешении цвет получается путем покрытия ЭЛТ люминофором, и сложение цветов делает итоговый цвет ярче. Поэтому, чтобы получился белый, должны присутствовать все три цвета в соответствующей пропорции. Получающиеся в результате цвета производятся путем сложения цветов.

Когда цвета смешиваются путем вычитания, мы используем бумагу или акриловое волокно в качестве вторичного источника света (отраженного), и цвета смешиваются в нашем глазу после того, как они отражаются от поверхности. Если мы смешиваем (путем сложения) все основные цвета, то получаем более темные цвета, а не более яркие. Цвета смешиваются отраженным светом, чей цвет определяется пигментом, который поглощает (вычитает) длину волны его поверхности.

Но вернемся к телевизору. В качестве основных, как уже упоминалось, используются три цвета: красный, зеленый и синий (RGB).

Рис. 2.13 . Цветное изображение в телевидении создается при помощи тройных точек из кристаллического люминофора (RGB )

Теория телевидения и многочисленные эксперименты демонстрируют, что с помощью этих трех основных цветов можно передать большинство естественных цветов (но не все).

Очевидно, внутри цветной ЭЛТ имеются три разных люминесцентных слоя, каждый из которых излучает собственный цвет во время электронного облучения.

Три основных люминесцентных слоя имеют различные свойства яркости, то есть равная интенсивность пучка производит неравную яркость. Чтобы компенсировать эти несоответствия основных люминесцентных слоев, все цветные телевизоры и мониторы оснащены специальной матричной схемой, которая умножает каждый цветовой канал на соответствующее корректирующее число.

Это демонстрирует самое известное уравнение яркости цветного ТВ, которое с помощью электроники применяется к трем основным сигналам в ЭЛТ:

L = 0.3R + 0.59G + 0.11B (28)

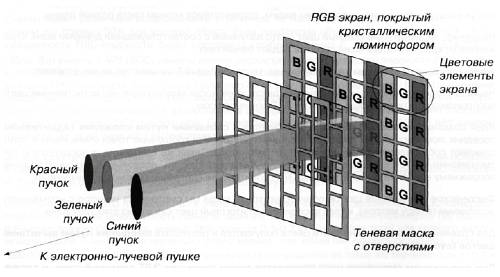
Рис. 2.14. Теневая маска RGB

Синий люминофор производит больше света, чем другие два, и поэтому, чтобы уменьшить его яркость и уравнять с двумя другими элементами, его надо умножить на 0.11. В этой книге мы не будем слишком углубляться в теорию цветов в телевизоре, поскольку это тема отдельной книги, но читателю важно оценить сложность проблемы и понять, что все цвета в телевизоре получаются путем визуального аддитивного смешения (сложения) трех основных цветов люминофора ЭЛТ: красного, зеленого и синего.