Действия над матрицами

Сложение матриц

Пусть матрицы A и B имеют одинаковый размер m´n, т.е.

, .

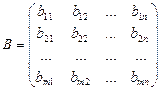Матрица C размера m´n называется суммой матриц A и B, если

, ,

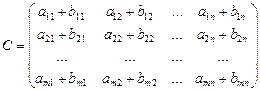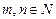то есть чтобы сложить матрицы одинакового размера, необходимо сложить их соответствующие элементы.

Умножение матрицы на число

Чтобы умножить матрицу на число, необходимо каждый элемент матрицы умножить на это число.

, , .

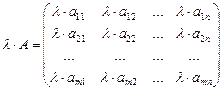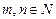Умножение матриц

Произведением матрицы A размера m´n и матрицы B размера n´k называется матрица C размера m´k, имеющая следующий вид:

,

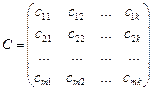где , , .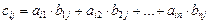

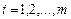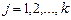Замечание II.1. Отметим, что умножение матриц определено, если число столбцов первой матрицы равно числу строк второй матрицы.

Замечание II.2. Из правила умножения матриц следует, что, вообще говоря, 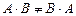, то есть умножение матриц не коммутативно.

Пример II.1. Заданы матрицы

, .

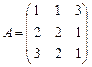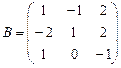Найти, если это имеет смысл, А+В, А×В, В^Т.

Решение.Так как матрицы квадратные, то для них все эти операции выполняются. Определим сумму матриц A и B, для этого вычислим суммы соответствующих элементов:

.

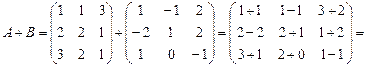
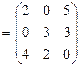Вычислим произведение:

.

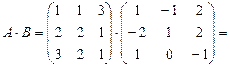
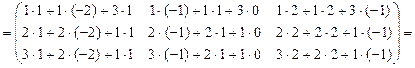
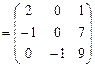Для транспонирования матрицы B необходимо поменять местами соответствующие строки и столбцы:

.

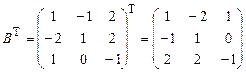Упражнение. Выяснить, какие из предложенных операций примера 1.1 выполнимы, если размерность матрицы A – m´n, а матрицы B – n´k.