Множество комплексных чисел

В XVI в., в связи с изучением кубических уравнений при выводе формулы для нахождения их корней, появлялись корни арифметические из отрицательного числа, хотя конечный результат давал действительный корень уравнения.

Своим введением в математику комплексные числа обязаны желанием извлечения корней четной степени из любого действительного числа, и отрицательного в том числе.

Самого по себе желания, конечно, недостаточно, тем более, что в то время потребности практически всегда вполне удовлетворялись вещественными числами. Уже отмечалось, что если решать уравнения традиционными методами, то в процессе преобразования до результата встречался квадратный корень из отрицательного числа (например, в формуле Кардано), хотя конечный результат был числом действительным. Поэтому корни из отрицательных чисел использовались без объяснения причин, а получаемые промежуточные числа называли мнимыми.

В конце 18-го века Ф. Гаусс (1777-1855) ввел комплексные числа, дал им геометрическую интерпретацию и доказал (1799) в частном случае основную теорему алгебры, о том, что каждый многочлен с действительными коэффициентами имеет хотя бы один действительный или комплексный корень.

Будем считать, что известны множество вещественных чисел и правила действий над ними. Рассмотрим уравнение 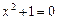. Применяя к нему обычные правила нахождения корней, получим 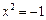. Допуская, что решение этого уравнения существует и 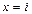, мы приходим к тому, что 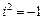. В области действительных чисел такого числа нет. Тогда, объявляя i новым числом, мы присоединяем его к множеству действительных чисел. 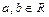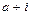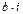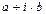Предполагая выполнение для этого числа операций сложения и умножения, мы будем иметь для любых числа , , , хотя 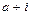– частный случа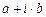й при 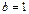. Тем самым мы получили новые числа 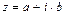, где 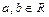. Выражение 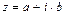называется алгебраической формой записи комплексного числа z. Отсюда следует, что множество действительных чисел есть подмножество нового числового множества – комплексных чисел. Таким образом, множество комплексных чисел

, .

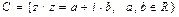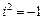Оправдалось предположение Дж. Кардано: с мнимыми числами можно действовать по правилам обычной алгебры, то есть писать, при 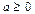, 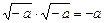. Пусть комплексное число 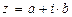, тогд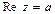а , а 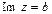, где Re сокращение от Real (действительный), а Im – от Imaginares (мнимый). Говорят, 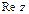– действительная часть, 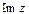– мнимая часть комплексного числа z. Эти обозначения введены для удобства работы с комплексными числами [3, 7].

Отталкиваясь от алгебраической формы записи комплексного числа, определим поле комплексных чисел. Пусть даны два комплексных числа 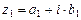, , 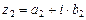, , 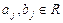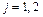тогда

1) 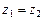Û , ;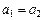

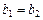2) ;

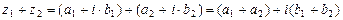3)

;

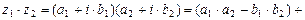
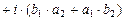4)

.

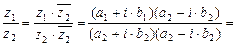
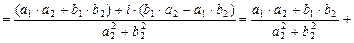
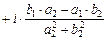Число 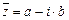называется комплексно сопряженным числу 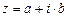, при этом .

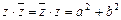Модулем комплексного числа 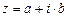называется действительное число .

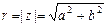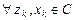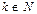, , имеет место:

1) ;

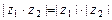2) 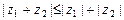(неравенство треугольника);

3) 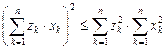(неравенство Коши-Буняковского).

Геометрически комплексное число z представимо точкой A на плоскости с заданной декартовой системой координат. Ось Ox называется действительной осью, а ось Oy – мнимой, тогда для 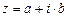ставится в соответствие точка 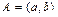или вектор 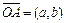, , 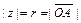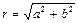(рис. I.1).

Из рис. I.1 следует, что 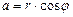, 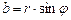. Угол j называется аргументов 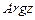комплексного числа 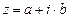. Значение аргумента, удовлетворяющего условию 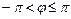, называется главным значением аргумента комплексного числа zи обозначается 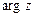, тогда , .

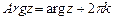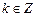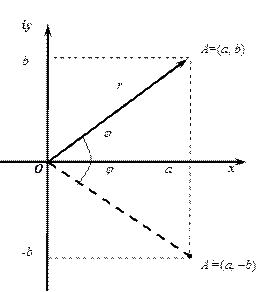
Рис. I.1

Выражени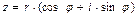е , где 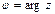, называется тригонометрической формой записи комплексного числа .

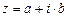Учитывая формулу Эйлера [3, 5]: 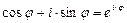, получаем, что 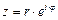– показательная форма записи комплексного числа; заметим, что 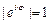и , .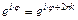

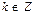Таким образом, комплексное число имеет три формы записи: алгебраическую, тригонометрическую и показательную.

Возведение комплексного числа в целую степень n легко осуществить по формуле Муавра [3, 5]:

.

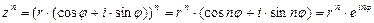В частности, при 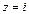имеем 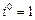, , 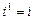, , 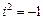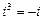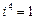и т.д.

Эта же формула справедлива и для отрицательного показателя степени: учитывая, что 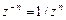, получим

.

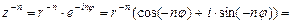
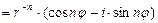Например,

.

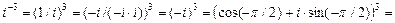
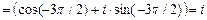Для извлечения корня из комплексного числа воспользуемся формулой:

,

, .

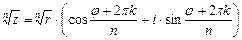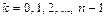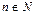Пример I.4. Найти .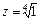

Решение.Модуль комплексного числа z равен ,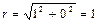

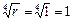. Поскольку 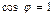, , 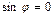тогда 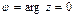. Применим формулу

,

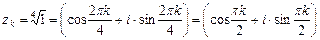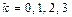
и получим

1) , ;

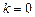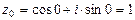2) , ;

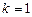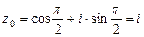3) , ;

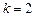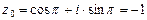4) , .

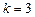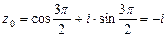При других значениях k корни повторятся (см рис. I.1)

Дальнейшие обобщения числа ни к чему принципиально новому не привели. В конце 19-го века выяснилось, что для выхода за пределы множества комплексных чисел следует отказаться от каких-либо обычных свойств числа, конечно, если это будет возможным.

Девятнадцатый век и начало двадцатого оказались очень плодотворными для математики. Произошло ее аксиоматическое построение на теоретико-множественной основе. К тому времени появилось достаточно много математических теорий, и все они, как было замечено, изучали ту или иную алгебраическую систему как обобщение числовой, то есть некоторое множество элементов с операциями умножения и сложения не в смысле арифметических действий с конкретными элементами, а в смысле свойств (аксиом), которыми они определяются.