LR – форма представления нечетких чисел

Нечеткие числа и операции над ними

Принцип обобщения:

Он дает формальный аппарат для переноса операций над обычными или четкими множествами на нечеткие множества.

Ω, Ω₁ или X,Y два универсальных множества

f: Ω(X) Ω(Y)

Ă – нечеткое множество ĂÍ Ω

Тогда f: Ă Č, ČÍ Ω₁

Функция принадлежности μ_с (Y)= sup μ_Ă(x); f ^–1 (y)=0; y=f(x)

0, f ^–1 (y)=0

Пример:

Ω={1;2;3;4}

Ω₁={1;2;3;4;5;6}

y=x+2

Ă={(1;0,1), (2;0,2), (3;0,7), (4;1)}={0,1/1; 0,2/2; 0,7/3; 1/4}

Č=?

S_B={3,4,5,6}

μ_B(3)=0,1

μ_B(4)=0,2

μ_B(5)=0,7

μ_B(6)=1

B={0,1/3; 0,2/4; 0,7/5; 1/6}

Нечеткие числа

Определение: Нечеткое число есть нечеткое множество А определенное на множестве действительных чисел (АÍ R), такое что его функция принадлежности μ обладает следующими свойствами:

1. Она нормальна

sup μ_A(x)=1

2. Выпукла

x≤y≤z μ_A(y)≥min { μ_A(x), μ_A(z)}

Примеры нечетких множеств: <около 5>,<чуть больше 6>

Тогда в соответствии с принципом обобщения арифметические операции над нечеткими числами могут быть представлены следующим образом:

* - символ арифметической операции это может быть (+, - , /, ^. )

z=x*y

μ_A*B(z)= max {min μ_A(x), μ_B(y)}

z=x*y

или

μ_A+B(z)= max {min μ_A(x), μ_B(y)}

z=x+y

μ_A/B(z)= max {min μ_A(x), μ_B(y)}

z=x/y

y≠0

μ_A-B(z)= max {min μ_A(x), μ_B(y)}

z=x-y

Существуют и другие способы задания нечетких множеств и соответственно нечетких чисел, и соответствующее этим способам представлений арифметических операций.

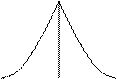
LR – форма представления нечетких чисел

L – Left

R – Right

То есть интервальное представление

a_А b_А

m_A

Тогда LR представление нечеткого числа есть тройка

А:=<m_A, a_А , b_А >

m_A – среднее значение нечеткого числа А

a_А – отклонение слева

b_А - отклонение справа

Тогда функция принадлежности может быть записана следующим образом:

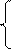L((m – x)/ a) , a>0, x≤m

m_А(x)= 1, x=m

R((m-x)/ b) , b>0, x>m

В этом случае арифметические операции над нечеткими числами определяются как операции над тройками.

Сложение двух нечетких чисел:

А+B := (m_A, a_А , b_А)+( m_B, a_B , b_B)=(m_A+ m_B, a_А+a_B , b_А+ b_B)

Операция вычитания:

А – B := (m_A, a_А , b_А) - (m_B, a_B , b_B)=(m_A- m_B, a_А+a_B , b_А+ b_B)

Операция умножения:

А ^. B := (m_A, a_А , b_А) ^. ( m_B, a_B , b_B)=(m_A^. m_B, m_A^. a_B+m_B^. a_A , m_A^. b_B+m_B^. b_A)

В том случае, когда функции принадлежности линейны, то фактически мы имеем треугольные нечеткие числа и функция принадлежности будут записана следующим образом:

m_А(х)= (х-а^-)/(а-а^-), а^-≤х<a

(а⁺-х)/(а⁺-а), а⁺<x≤а

a^- a a⁺

Функция принадлежности может быть вида:

α Ŝ Š β

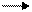
(а^- ) (а⁺)

Таким образом нечеткое число Ã:= < Ŝ_А, Š_А, α_А, β_А> либо Ã:= < Ŝ_А, Š_А, а^-, а⁺>

Тогда функция принадлежности:

m_Ã(х) = (х- а^- )/( Ŝ-а^-), а^-≤x< Ŝ

1, Ŝ≤x≤ Š

(а⁺-х)/(а⁺- Š), Š<x≤a⁺

Свойства арифметических операций

Сложение и умножение коммутативны, ассоциативны, но в общем случае не дистрибутивны.

Нечеткое число А не имеет противоположного ему числа и не имеет обратного числа (то есть нет –А и нет А^-1)