Положительные и отрицательные нечеткие числа

Унимодальное нечеткое число А называется положительным если для любого х принадлежащего носителю S_A , х>0.

В противном случае нечеткое число будет отрицательным, то есть х <0

Выпуклое нечеткое число называется нечетким нулем если m_А(0)=sup m_А(x)

х

Арифметические операции над нечеткими числами можно выразить через представление с помощью α уровневых подмножеств.

Справедливо следующее утверждение:

- если для любого α принадлежащего отрезку [0,1] и арифметическая операция * является расширенной бинарной операцией и нормальные унимодальные нечеткие числа А, В, С такие что их m_А, m_В, m_С М(R) (множество всех нечетких подмножеств на числовой оси) имеют носители такие что, либо для любого х, х S_A,B,C , x>0, либо для любого х, х S_A,B,C , x<0, то будет справедливо следующее выражение

С=А*В= 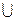α[δ_С(α), γ_С(α)]

α

Где δ_С(α)= δ_С= inf [δ_A * δ_B, δ_A * γ_B, γ_A * δ_B, γ_A * γ_B]

γ_C(α)= γ_C = sup [δ_A * δ_B, δ_A * γ_B, γ_A * δ_B, γ_A * γ_B]

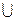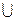≡ , δ_A(α)≡δ_A, γ_A(α) ≡ γ_A, δ_B(α)≡δ_B, γ_B(α) ≡ γ_B (≡ - однозначно)

α 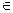[0,1 α

В этом случае арифметические операции над нечеткими числами будут иметь следующий вид:

А+В = Uα[A_α+B_α]= Uα[δ_A + δ_B, γ_A + γ_B] ;

α α

А ^. В = Uα[A_α ^. B_α]= Uα[δ_A ^. δ_B, γ_A ^. γ_B] ;

α α

А - В = Uα[A_α -B_α]= Uα[δ_A - γ_B, γ_A - δ_B] ;

α α

А / В = Uα[A_α /B_α]= Uα[δ_A / γ_B, γ_A / δ_B] ;

α α

при таком представлении арифметических операций над нечеткими числами операции над нечеткими числами в LR – форме является частным случаем операции над α уровневыми множествами.

Рассмотрим указанные операции над нечеткими числами в LR форме в несколько другом виде:

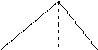α а β γ в δ

Если нечеткое число Аº(а, α, β) и Вº(в, γ, δ)

Сложение:

(а, α, β)_LR+ (в, γ, δ)_LR=(а+в, α+γ, β+δ)_LR

Вычитание:

Если – (а, α, β)_LR=(- а, β, α)_RL то

(а, α, β)_LR - (в, γ, δ)_LR=(а-в, α+δ, β+γ)_LR

Умножение:

1. μ_А, μ_В 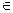М(R), а>0, в>0

(а, α, β)_LR^. (в, γ, δ)_LR=(ав, аγ+вα, аδ+вβ)_LR

2. μ_А, μ_В 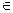М(R), а<0, в>0

(а, α, β)_RL^. (в, γ, δ)_LR=(ав, вα-аδ, вβ-аγ)_RL

3. μ_А, μ_В 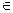М(R), а<0, в<0

(а, α, β)_LR^. (в, γ, δ)_LR=(ав, -вβ-аδ, -вα-аγ)_RL

Прежде чем определить операцию деления определим обратное к A нечеткоt число

Если А нечеткое число то для любого А, μ_А 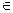М(R), а>0

(а, α, β)_LR^-1=(1/a, β/a², α/a²)_RL

тогда деление:

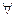А, В такие что μ_А, μ_В 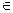М(R), а>0, в>0

(а, α, β)_LR^. (в, γ, δ)_LR=(а/в, (аδ+вα)/в², (аγ+вβ)/в²)

указанные выражения можно применять при малых значениях α, β, δ, γ