А сами «сгустки цифровых форм», которые имеют в ряду «Ф» свои аддитивные «числовые» проявления, в терминах обычной математики мы называем обычно … числами ряда.

Волны упорядочиваются по закону простых чисел

Если продольные волны обладают столь примечательным свойством взаимопроникновения (см. выше), то не следует ли рассматривать результаты их воздействия на что-либо, как суммарное воздействие всех и каждого из колебаний, определяемых раздельно?

Иначе говоря, не являются ли такие независимые компоненты сложного продольного колебания характерными «гармониками», слагающими некий общий «спектр» продольного воздействия?

Подобно тому, как наборы излучений (различного цвета) от излучающего объекта образуют характерные «спектры излучений».

Присутствующие в таких «спектрах излучения» гармонические компоненты тоже не подвержены смешению и именно это свойство применяют люди, когда фиксируют и изучают «спектрограммы».

От этой аналогии родилась мысль о том, что и в математике должна найтись некая числовая процедура, отражающая идею продольного и поперечного видоизменения (волнового процесса).

Если мы исследуем, например, периодический ряд чисел Фибоначчи, представленный в нумерологической (цифровой) форме, то, следуя логике нашего изложения, можно увидеть, что мы изучали как раз таки «поперечные» закономерности этого ряда (см. группировки по 1,2,3 и 4 разряда на Рис.5).

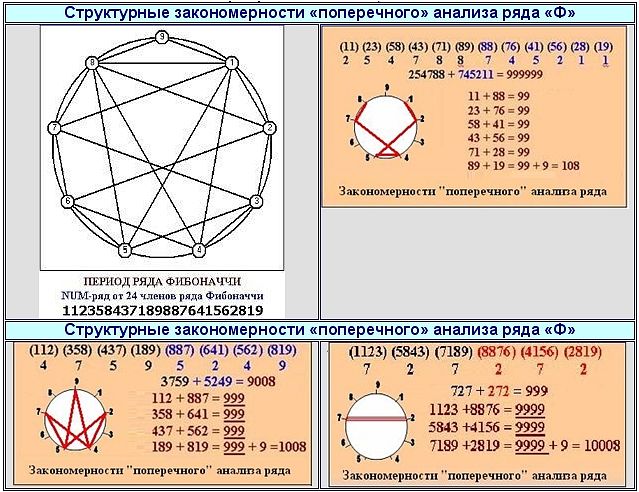
Рис.5

Действительно, поскольку ряд Фибоначчи «прирастает» и видоизменяется слева – направо, в согласии со строчной записью этого ряда, то сделанные для анализа, на рисунках выше, группировки членов ряда (по 2,3 и 4) являются «срезами» статически уже развёрнутого, полностью сформировавшегося ряда, и поэтому отражают поперечный характер анализа данного ряда. Никакой динамики становления этого ряда в этих данных не отражается.

Мы «выхватили» из ряда (уже прошедшего все стадии развития!) определённые группы цифр и установили закономерные отношения в суммах этих цифр, а также в суммах зеркальных частей всего 24-значного периода ряда «Ф».

Честно говоря, это было само по себе удивительным результатом, который, вообще говоря, совершенно не был очевиден, даже в цифрах, и уж тем более в числах.

«Главная заслуга» в обнаружении периодичности ряда Фибоначчи принадлежит … необыкновенным свойством самого ряда, который буквально «нашпигован» закономерностями самого невообразимого рода.И сейчас мы снова в этом убедимся.

Уже отмечался тот момент в рассуждениях, что ряд Фибоначчи (даже в его статической записи) есть образ некоторого периодического процесса «прироста» значений каждой последующей цифры (числа) по отношению к двум предыдущим цифрам (или числам).

Отсюда следует, что можно и должно исследовать динамику и закономерности развития всего ряда «Ф» в целом, а также по частям.

А это означает, что необходимо вести анализ продольных закономерностей ряда.

Если обратиться к предыдущему (поперечному) анализу, то нужно опереться на его результаты, которые говорят, в частности, о наличии закономерностях цифр, связанных с разными поперечными группировками (и их симметрией).

И коль скоро закономерность однотипных группировок по всему периоду ряда «Ф» обнаруживается, то должна существовать и другая закономерность, которая будет отражать динамику «прироста» и формирования этой самой первой («поперечной») закономерности.

И тогда, с учётом этой идеи о развитии ряда (при формировании и считывании), можно сказать, что некий «продольный алгоритм устроения ряда» порождает другой, «поперечный порядок устроения» данного ряда, обнаруженный нами ранее.

Таким образом, как только мы определимся со способом отражения продольной динамики развития ряда «Ф», мы получим в свои рукисовершенно новый подход и инструмент для анализа числовых рядов.

Более того, этот подход повлечёт за собой необходимость углубления некоторых наших представлений о ряде понятий. В частности, понятия о «числе».

Однако, сформулируем для начала главную задачу первого этапа исследования.

Как отмечалось выше, мы пытаемся утвердить правомерность и продуктивность нетрадиционного волнового подхода к анализу рядов, и это - основной предмет исследований.

Практически же, в рамках волнового подхода, определяется способ реализации идеи «продольного» числового анализа.

А в качестве результата мы надеемся научиться вычислять…

гармонические компоненты, например, спектральные гармоники золотогоряда Фибоначчи

Сказанное про «гармоники» - это важное методологическое обстоятельство.

Поскольку, как только мы определим, рассчитаем и отобразим графически особую картину продольных «движений» (изменений) чиселряда Фибоначчи, то получим то же самое, что в физике называют «гармоническим спектром» сигналов.

По этой причине такого рода гармоники я обязан буду назватьгармоническим числовым «спектромряда»Фибоначчи.

Но, ранее мной уже было введено в оборот другое, подобное понятие о «числовых спектрах», которое было сформулировано и обосновано в работах [1,3,11].

Отсюда возникает необходимость чёткого различения этих, близких по звучанию, понятий друг от друга, что я сейчас и сделаю в рамкахпредставлений числонавтики и эзотерической математики.

В случае со «спектрами чисел» [1] мы говорим о тех компонентах чисел, которые объективно слагают эти числа и которые определяются в результате специально модифицированной числовой манипуляции по алгоритму «русского умножения».

Привычнее - с помощью оператора бинарного разложения, хотя, если говорить строго, это не одно и то же!

А в новом случае мы говорим о спектреряда Фибоначчи, а не числа,т.е. о наборахизменяющихсячисел неких составных рядов, которые все вместе отражают анализируемый ряд Фибоначчи.

И такого рода «спектр» складывается из набора компонент (гармоник), получаемых в результате обработки исходного ряда с помощью совсем другой числовой манипуляции (алгоритма действия).

Суть новой числовой манипуляции по обработке данных рядов состоит в том, что она реализует идею независимого сосуществования (и движения, развития) некоторых элементарных числовых рядов.

А также идею их совместного проявления в форме удивительного периодического явления - феномена ряда Фибоначчи.

Помните? Выше подчёркивалось, что продольные колебания – взаимно независимы, а их совместное проявление нужно оценивать в соответствии с принципом аддитивности.

Именно поэтому все числа ряда Фибоначчи нужно теперь трактовать, как некие особые «сгустки» более простых (элементарных) «цифровых форм». Такие «сгустки» есть результат аддитивного «слияния» неких «продольно изменяющихся» (в одном направлении), элементарных «цифровых форм», сиречь гармоник исходного ряда Фибоначчи.

А сами «сгустки цифровых форм», которые имеют в ряду «Ф» свои аддитивные «числовые» проявления, в терминах обычной математики мы называем обычно … числами ряда.

Указанные цифровые формы (гармоники), по своей сути являясь тоже цифровыми рядами. И это именно они совместным действием порождают совокупный, общий ряд «чисел» Фибоначчи.

Естественно, что при этом будет уместным спросить: «А почему числа ряда Фибоначчи, да и сам этот ряд, коль скоро он так устроен, не … «разваливаются»? Ведь они «составлены» из каких-то наборов, тем паче – независимых, гармоник?

Что их «скрепляет» между собой и заставляет устойчиво существовать в форме таких «сгустков-чисел»?

Предварительный ответ здесь может быть такой: «Аналогия с продольными волнами (в средах распространения) от разночастотных гармонических источников колебаний справедлива и для числовых проявлений.

Синонимом «среды» у нас может быть т.н. «числовой континуум», где существуют, распространяются и разнообразно взаимодействуют эти самые элементарные гармонические цифровых формы; они участвуют в передаче соответствующих возмущений, а в целом – во всякого рода«вселенском счёте».

И в такой картине вовсе не обязательным является представление о «навечно зафиксированном» виде ряда Фибоначчи.

Более вероятно, что именно в силу совокупного действия одного определённого набора элементарных цифровых форм мы видим конкретные материализации числовых феноменов в физические процессы и объекты, которые описываются алгоритмами и рядами, соответствующими золотым рядам Фибоначчи.

Но стоит такому набору измениться, как тут же мы увидим иные варианты материализации «золотых» рядов, чьё многообразие давно уже требует некой теоретической системы представленийо законах смены и трансформаций одних рядов в другие, одних «форм проявления» (материализации) – в иные формы.

Кроме того, во весь рост встаёт и другая проблема.

Это - проблема познания тех самых Первичных Сил, которые все эти «формы» порождают и управляют ими. Но этого мы, увы, пока точно не знаем. Мы только подступаемся к этой проблеме.

Тем не менее, фактическое, хотя и вторичное проявление данных Сил (и форм) мы теперь можем не только созерцать (в феномене «всеобщей счислимости»), но и использовать («фильтровать») – в виде анализа гармоник (компонент) рядов Фибоначчи.

Делать это можно на основе представляемого автором ниже метода, который применим не только к ряду Фибоначчи, но и к рядам любого рода.