Исчисление нечетких интервалов
Определение: нечеткий интервал это выпуклая нечеткая величина, функция принадлежности которой квазивогнута.
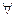 U, V
U, V 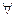 ω
ω 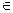 [U,V]
[U,V]
μA(ω)≥min (μA(U), μA(V))
Параметрически нечеткий интервал S определяется следующим образом:
 | |||
 | |||
l α β r
 |
Ŝ Š
S:=<Ŝ, Š, l,r>
[Ŝ, Š] – ядро
Ŝ, Š – нижние и веррхние модальные значения нечеткого интервала S
l – неубываемая функция удовлетворяющая следующим условиям
l= 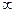 если α=0
если α=0
l-1(1)=Ŝ
l-1(1) - l-1(0)=α – левый коэфициент нечеткости
r – невозрастающая функция удовлетворяющая условиям:
r= 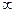 если β=0
если β=0
r-1(1)=Š
r-1(0) - r-1(1)=β – правый коэфициент нечеткости
если α= 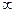 то l=1
то l=1
если β= 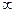 то r=1
то r=1
Определение: Ядро нечеткой величины А называется множество JA=(ω 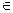 Ω, μА(ω)=1)
Ω, μА(ω)=1)
ω 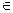 JA при этом всякое действительное число ω принадлежащее JA называется модальным значение А.
JA при этом всякое действительное число ω принадлежащее JA называется модальным значение А.
Функция принадлежности нечеткого интервала S определяется следующим образом:
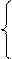 |
μS(U)= l(U), U≤Ŝ
1, Ŝ≤U≤ Š
r(U), U≥Š
Поскольку Ŝ= l-1(1) , Š= r-1(1), l-1(1) - l-1(0)=α, r-1(0) - r-1(1)=β то при α≠0 и β≠0 в представлении нечеткого интервала значения Ŝ и Š можно не указывать, тем не менее для полноты нечеткого интервала мы их будем указывать.
В практических расчетах в зависимости от условий символ 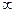 можно трактовать как либо очень большое, либо как очень маленькое число, либо вообще игнорируется при сравнении нечетких интервалов по левому или правому краю.
можно трактовать как либо очень большое, либо как очень маленькое число, либо вообще игнорируется при сравнении нечетких интервалов по левому или правому краю.
При подробном представлении носитель нечеткого интервала выбирается таким образом, чтобы гарантировать “невыход” рассатриваемой величины за нужные пределы, а его ядро будет содержать наиболее правдоподобные значения. Для унимодального нечеткого интервала подмножество α – уровня будет иметь следующее выражение:
Sα=[ l-1(α), r-1(α)]
 | |||
 | |||
 α β
α β
Ŝ Š
Нечеткий линейный интервал (функции r, l линейны) представляется в виде:
S:= <Ŝ, Š, α, β>
Для представления стандартной нелинейной нечеткой величины иногда пользуются нормальным или экспоненциальным представлением, а чаще всего унимодальной квадратичной функцей следующего вида:
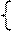 μ (u, в, а, с)= μ1(u, в, а) , в≤u≤а
μ (u, в, а, с)= μ1(u, в, а) , в≤u≤а
μ2(u, в, с) , а≤u≤с
 |
μ1(u, в, а)= 2(u-в)2/(а-в)2 , в≤u≤(а+в)/2
1- 2(а-u)2/(а-в)2 , (а+в)/2≤u≤а
 μ2(u, а, с)= 1- 2(а-u)2/(а-с)2 , с≤u≤(а+с)/2
μ2(u, а, с)= 1- 2(а-u)2/(а-с)2 , с≤u≤(а+с)/2
2(u-с)2/(а-с)2 , (а+с)/2≤u≤с
Эта функция обладает вырожденным ядром, то есть Ŝ=Š=а, LR – форма но в нелинейном виде.
 | |||
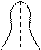 | |||

в а с
Для невырожденного ядра:
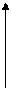 | |||||
 | |||||
 |
в а1 а2 с
 μ1 (u, в, а1) , в≤u≤а1
μ1 (u, в, а1) , в≤u≤а1
μ(u, в, а1, а2, с) = 1, а1≤u≤ а2
μ2 (u, а2, с) , а2≤u≤с
 μ1(u, в, а)= 2(u-в)2/(а1 -в)2 , в≤u≤(а1 +в)/2
μ1(u, в, а)= 2(u-в)2/(а1 -в)2 , в≤u≤(а1 +в)/2
1- 2(а1 -u)2/(а1 -в)2 , (а1 +в)/2≤u≤а1
 μ2(u, а, с)= 1- 2(а2 -u)2/(а2 -с)2 , с≤u≤(а2 +с)/2
μ2(u, а, с)= 1- 2(а2 -u)2/(а2 -с)2 , с≤u≤(а2 +с)/2
2(u-с)2/(а2 -с)2 , (а2 +с)/2≤u≤с
В введенных обозначениях нечеткого интервала L(u) будет определяться:
 |
L(u) = 2(u-(Ŝ-α))2/α2, Ŝ-α≤u≤Ŝ-α/2
1-2(Ŝ-u)2/α2, Ŝ-α/2≤u≤Ŝ
 R(u) = 1-2(Š-u)2/β2, Ŝ≤u≤Š+β/2
R(u) = 1-2(Š-u)2/β2, Ŝ≤u≤Š+β/2
2(u-(Ŝ+β))2/β2, Ŝ+β/2≤u≤Ŝ+β
Ŝ=а1, Š=а2, Ŝ-α=в, Š+β=с
Дата добавления: 2016-01-09; просмотров: 1276;
